采用小波变换的脑电图信号分析及其应用

蔡琼，陈鹏慧，魏武

（1.湖南信息职业技术学院 电子工程学院，湖南 长沙410200；2.华南理工大学 自动化科学与工程学院，广东 广州510641）

1929年，自德国精神病医生Berger进行人的脑电图（EEG）信号的最早期研究后，EEG 就一直被用作一个临床诊断和研究的工具［1］.EEG 检查对神经系统疾病诊断、病情监测及疗效观察有重大作用.通过脑电波就可以发现异常生物电，通过仪器还原，可以发现哪部分大脑发生了疾病［2］.因此，EEG 检查己广泛应用于临床医学、心理学和认知神经科学的研究中.EEG 自动识别方法主要有Lyapunov指数法［3］与时频分析法.无论是谱分析的方法，还是非线性动力学的方法，在研究EEG 信号时都要求信号是平稳的.但EEG 信号是非线性非平稳信号，这就对连续的动态分析形成了挑战.于是，以如维格纳分布等时频分析为代表的非平稳分析方法引起了人们的极大兴趣.然而，对于多通道分量EEG 信号而言，维格纳分布的时间、频率双线性会使其存在严重的交叉项干扰，阻碍其对EEG 信号的有效分析及分量参数的提取，大大降低自动识别的效果，从而影响了维格纳分布在EEG 信号中的应用与推广［4］.小波分析是由Grossman和Morlet引入到信号分析领域的.由于神经生物科学和计算机信息科学的交叉融合，小波分析才在EEG 信号消除噪声、信号分析、特征检测、自动识别等领域中引起关注［5］.本文将能适应不同波形的多小波基（小波母函数序列）代替小波变换中的单个小波母函数，然后用支持向量机的方法进行分类，并应用于典型的脑电波EEG 信号的自动识别中.

1 基于小波变换的EEG 分析

小波基函数（母函数）选取及计算尺度a（分辨率）的选取都是小波分析过程中亟待解决.有限带宽的EEG 脑电波信号在某一尺度下的小波相当于一个带通滤波器［6］，若此带通滤波器用来分析EEG 信号，则在频域空间上必须与待分析的EEG 信号有交集，具体分析模型为

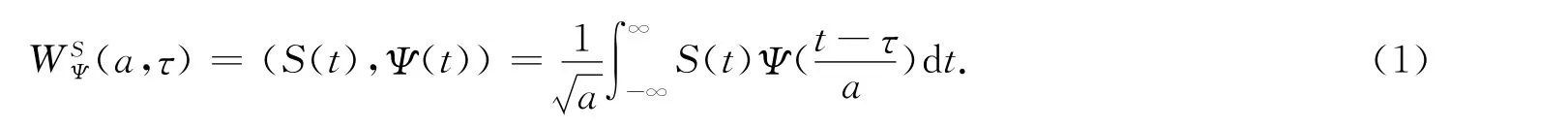
选取EEG 时频分析中最常用的非正交性Morlet复值小波为小波基函数，即

式（2）中：fc为小波的中心频率；fb为带宽参数.Morlet小波变换中的小波中心频率对应不同的带宽或分辨率.这是由于Morlet小波有一个恒定的比率K＝2fc／fb，实际应用中，fc／fb一般取值大于2.5.

在分析EEG 的阿尔法波形时候［7］，中心频率fc＝10Hz（阿尔法波峰值），阿尔法波随着时间变化的能量分布为

将EEG 信号与小波信号进行卷积平方并积分，通过实验数据分析得出，获取EEG 信号中阿尔法波与脑机能有一定的关系.

小波神经网络是基于小波分析而构造的一种新的神经网络模型［8］.在小波神经网络中的神经网络函数不再是传统的Sigmoid函数，而采用的是非线性小波基.脑电波信号重构的方法是通过将所选取的非线性小波基进行线性叠加来实现.脑电波信号S（t）可用非线性小波基进行拟合，即

式（4）中：wk，h（t），bk，ak分别为权值、小波基，平移因子和伸缩因子，k为小波基的个数.神经网络参数可以通过最小均方差能量函数进行优化，即

式（5）中：M为数据采样总数.这里选用Morlet母小波为小波基，该小波是余弦调制的高斯波，分辨率高.令t′＝（t－bk）／ak，则有

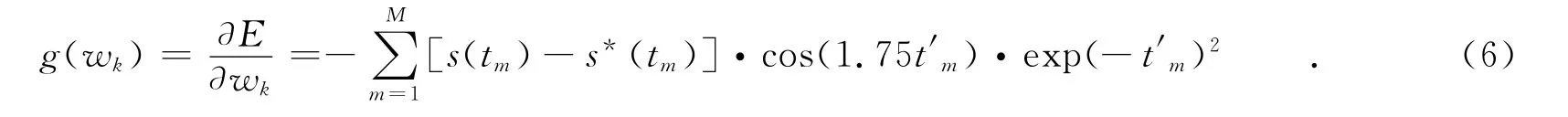
同理，g（bk）＝

采用共轭梯度法优化网络wk，bk，ak，分别令向量w＝（w1，w2，…，wk），g（w）＝（g（w1），g（w2），…，g（wk）），s（w）t为w第i次循环搜索方向，则有

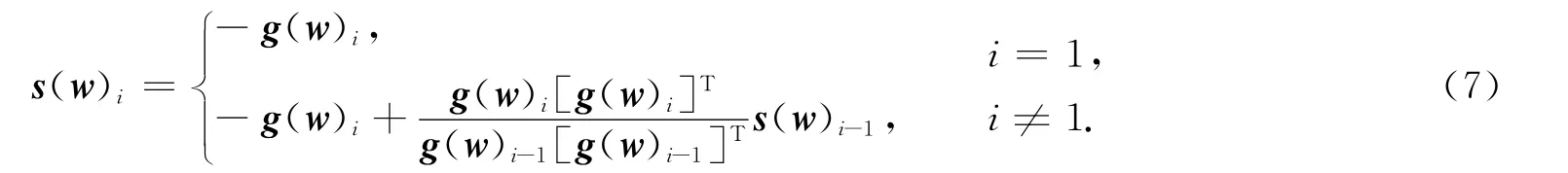
同理，定义s（b）i，s（a）i.

w按照如下公式进行调整，即

同理，b，a都可按照式（8）进行调整.

通过一维搜索变步长法，计算最佳步长αwi，αai，αbi，并按照最佳步长调节网络参数w，b，a，直到E满足特定误差为止.

该方法适合用于EEG 多通道复杂信号的分析，具有很好的信号特征提取和屏蔽随机噪声能力，有效信息有助于癫痫棘波、棘慢波的临床诊断.

2 基于小波变换的EEG 信号应用

2.1 EEG 信号的自动识别系统设计

所设计脑电波（EEG）自动识别系统，如图1所示.EEG 信号自动识别系统主要分为预处理、特征提取和分类三大模块.自动识别系统读取EEG 数据，选取合适小波基进行多分辨分析，并计算SWE（小波熵）值；然后，通过SVM（支持向量机）来进行不同病症的分类；最后，给出识别报告，即通过自动识别系统检测出病患脑电波是否为正常脑电波的结论.结合临床，如果是脑内伤患者，则在各导联会出现弥漫性的慢波，EEG 信号能量低，且阿尔法波的比列减少；如果出现棘波和棘慢波则考虑可能是癫痫.

2.2 采样数据及其预处理

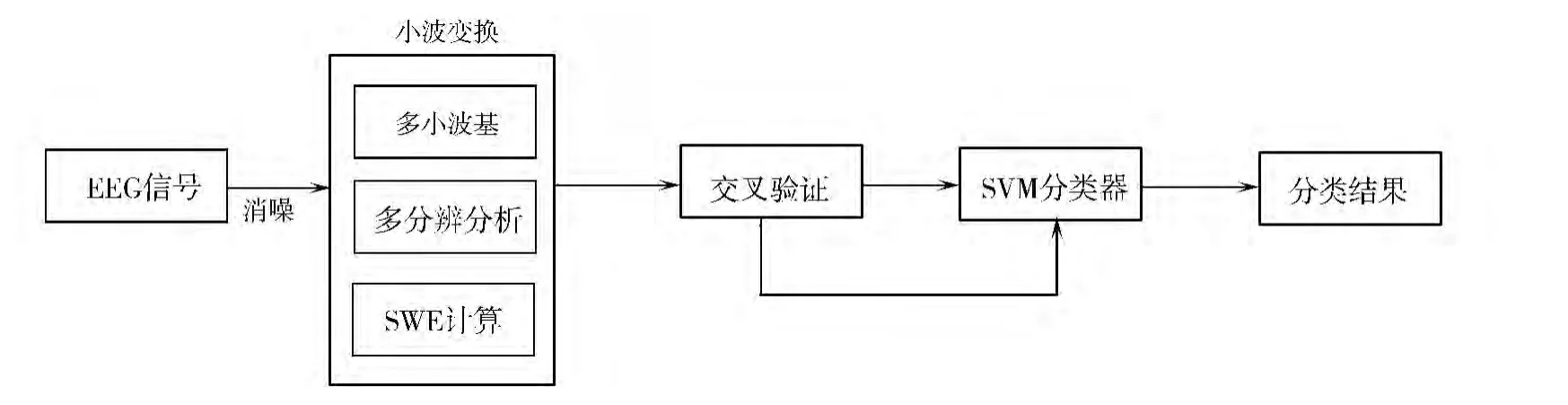
图1 脑电波自动识别系统框图Fig.1 EEG automatic identification system block diagram

多通道EEG 数据是中南大学湘雅医学院附属二医院精神科提供的.EEG 脑电波采用国际系统安置电极的仪器，采样频率fc为250Hz，头皮单导联为16通道，选取其中几个导联的数据.每组EEG 脑电数据记录时间为10s.EEG 采集仪系统已经进行了基本的消噪处理，图2为某位39岁健康男子的EEG 数据采样图.

图2 某健康男子EEG 的采样图Fig.2 Healthy man EEG sampling chart

2.3 小波变换

2.3.1 小波基的选取 计算各小波基对待分析EEG 的小波系数及方差值.在连续小波变换中进行多分辨分析的小波基有coif系小波、rbio系小波、haar小波、db系小波、dmey系小波、sym 系小波、bior系小波等.哪组小波基所获得小波系数最大且方差值小，就选取这组小波基.

2.3.2 多分辨分析 如果进行6层分解，则各分量所对应的子频带成分大致与EEG 脑电波中lowδ，highδ，θ，α，β，γ一一对应.采用6层分解后，一一对应的各频带具有明确的物理含义.因此，将EEG 的原始信号f（t）进行6层分解［9］，则有

小波系数长度向量Lcoef和小波分解系数向量Ccoef为小波变换分解后输出的结构.其中，系数向量Ccoef结构为

2.3.3 基于多小波基的小波熵计算 对用不同的频率子带计算其能量分布SWE值，则有

式（11）中：pj是在尺度j下的能量和所有尺度下能量和之比；cj，k为各尺度下的Ccoef.

2.4 支持向量机分类器的设计

支持向量机（SVM）的基本思想是如何解决一个非线性问题转换到另一个线性空间的问题［10］.这里需要的本库分为正常、癫痫、脑病、脑内伤，因此，要解决的就是一个4 分类问题（正常人EEG、癫痫EEG、脑血管EEG、脑病EEG）.

标准的SVM 是解决两类分类问题，文中采用的是“One Against One”SVM 分类法.该算法是将多分类问题（l类）转换为C2l（l（l－1）／2）个二分类SVM 问题.当SVM 分类器分类i，j类时，在训练样本中选取对应的训练样本（正常人EEG、癫痫EEG、脑血管EEG、脑病EEG），并将第i类记为正分类，第j类记为负分类，且满足

训练样本正常脑电波、癫痫脑电波、脑血管病脑电波、脑内伤脑电波各位50组.训练次数（n）与脑电波识别率（γ）对比，如图3所示.

2.5 性能对比

传统单小波基小波变换和文中设计方法（自适应多小波基小波变换、SVM 分类方法相结合）的性能对比，如图4所示.从图4中可以发现：文中方法分类效果要优于传统的单小波基的小波变换.

图3 训练次数与脑电波识别率对比图Fig.3 Training number and EEG recognition rate comparison chart

图4 各类脑电图分类正确率统计图Fig.4 All kinds EEG classification correct rate statistical chart

3 结论

利用小波变换进行EEG 的特征信号的提取时，先将小波基的选择进行了优化.文中采用的是自适应小波基的方法，匹配检测EEG 与各类小波基，取小波系数且方差值最小者.因此，对于待分析的EEG可能有多个不同的小波基进行小波分析.经过多分辨分析后，计算所获得的系数SWE 值，通过SVM 进行分类.通过实验表明：基于Morlet小波变换的自动识别和基于Coif3小波变换方法相比，文中采用方法的自动识别率要更高一些.

EEG 自动识别的应用领域不仅仅在临床医学上对癫痫、脑炎、帕金森、阿尔茨海默病、威尔逊［11］、脑瘤、癫痫、心律不齐等病的判定上［12］，还可应用于辅助治疗精神创伤、意志消沉等.在检测到特征波形时，可以进行相应的干预治疗，将检测、治疗自动智能化［13］.

EEG 自动识别还可以应用于提高人脸识别的身份验证的可靠性上.目前，用来进行身份识别方法和手段有很多，利用生物特征是比较安全可靠的方法.但是，如果这个人处于被胁迫的状态，那么单靠人脸识别的人脸检测就不够了.因此，可以利用人的脑电波和人脸识别技术相结合的方法提高安全性，保证信息的安全，使得系统的稳定性更高.

［1］BERGER H.Über das elektrenkephalogramm des menschen［J］.Arch Psychiatr Nervenkr，1929，87（1）：527－570.

［2］凌朝东，黄群峰，张艳红，等.脑电信号提取专用电极芯片的设计研究［J］.华侨大学学报：自然科学版，2007，28（3）：76－79.

［3］谢惠琴，王全义.时延细胞神经网络的指数稳定性和周期解［J］.华侨大学学报：自然科学版，2004，25（1），22－26.

［4］季忠，秦树人.基于Wigner分布的脑电信号处理［J］.信号处理，2002，18（6）：570－573.

［5］凌朝东，刘蓉，钱江，等.基于5／3提升小波变换的心电信号压缩算法及VLSI实现［J］.信号处理，2010，26（6）：930－935.

［6］杨帮华，颜国正，鄢波.基于离散小波变换提取脑机接口中脑电特征［J］.中国生物医学工程学报，2006，25（5）：518－521.

［7］王浩，陈志华，邹飒枫，等.基于Morlet小波变换的EEG 信号α波持续性的分析［J］.生物医学工程学杂志，2010，27，（4）：745－747.

［8］张永胜，刘爱萍，郁可.脑电信号数据压缩及棘波识别的小波神经网络方法［J］.生物医学工程学杂志，1999，16（2）：1－7.

［9］曾小军，黄宜坚.利用AR 模型和支持向量机的调速阀故障识别［J］.华侨大学学报：自然科学版，2011，32（1）：13－18.

［10］WALLACE B E，WAGNER A K，WAGNER E P，et al.A history and review of quantitative electroencephalography in traumatic brain injury［J］.J Head Trauma Rehabil，2001，16（2）：165－190.

［11］CHU N S，CHU C C，TU S C，et al.EEG spectral analysis and topographic mapping in Wilson′s disease［J］.J Neurol Sci，1991，106（1）：1－9.

［12］阮月平，张佃中，张屹.心律不齐患者心电图变异的小波分析［J］.生物医学工程学杂志，2012，29（4）：650－652.

［13］van COTT A C.Epilepsy and EEG in the elderly［J］.Epilepsia，2002，43（S3）：94－102.