应用小波变换和支持向量机的商业电力负荷预测

杨屹洲，方瑞明，黄文权，梁颖，汪亮

（1.华侨大学 信息科学与工程学院，福建 厦门361021；2.厦门埃锐圣电力科技有限公司，福建 厦门361002）

随着经济的高速发展和城市化进程的不断加快，商业用电在能源消耗中所占比重越来越大.对商业建筑电力负荷进行准确预测，能够使管理者及时掌握用电情况，灵活调整用电节能策略，这对于提高商业建筑的用电效率和节能降耗具有十分重要的意义［1］.目前，预测模型大多是依据天气和历史负荷数据对商业电力负荷进行预测［1－5］，常用的预测模型主要有：人工神经网络法、支持向量机法、时间序列法等.其中支持向量机（SVM）是根据结构风险最小化准则取得最小的实际风险，在电力负荷预测领域已取得了较好的效果［6－7］.商业建筑配电系统安装的数据采集系统SCADA（supervisory control and data acquisition）采集到的负荷数据表明：商业电力负荷有明显的日、周、月、年等周期变化的特性，包含规律性较好的低频分量；然而受到天气等随机因素的影响，又具有波动性较大的高频分量.单纯使用SVM模型对负荷进行预测，无法反映出众多不同规律的叠加影响，短期规律被极大削弱、甚至消失.而适当的小波变换能有效地分离和提取负荷不同的周期性、非线性和依赖关系，使每个分解序列都具有较好的规律性［8］.因此，本文提出了一种将小波变换和粒子群优化SVM相结合的组合预测模型——小波粒子群支持向量机（PSO－WSVM），并用其对商业电力负荷进行预测.

1 小波变换

多尺度小波分解可通过Mallat算法实现，即

式（1）中：cj和dj分别为低通滤波器和高通滤波器输出对应信号的高频部分（细节分量）和低频部分（近似分量），j＝0，1，…J，J为最大分解层数.

经滤波分解会产生多于原数据点的数据序列，因此，Mallat算法分解后的信号，可采用降采样的方法完整包含原信号的信息内容［9］.

2 支持向量回归算法

支持向量机算法应用于回归领域，先给定i组关系未知的样本（x1，y1），（x2，y2），…，（xi，yi），其中xi为输入向量，yi为输出值.采用的回归函数为

φ（x）将x映射到l维特征空间中，在该特征空间中进行线性回归，回归问题转化优化问题为

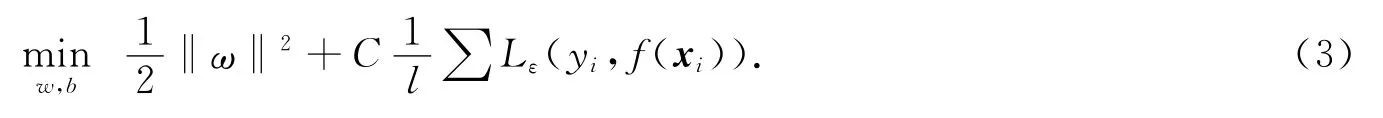
式（3）中：第1项是使函数更为平坦，从而提高函数的泛化能力；第2项为减小误差.采用ε不灵敏惩罚函数，常数C＞0控制对超出误差样本的惩罚程度，且有

寻找核函数K（xi，xj），可将问题转化对偶优化问题，即

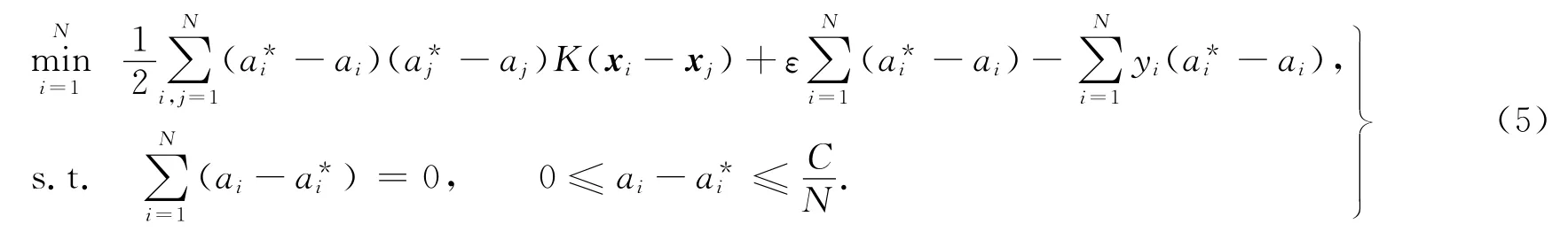
并求得最优解为

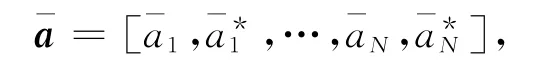
从而构造回归函数，有

3 预测模型

商业电力负荷预测预测流程图，如图1所示.预测过程为：1）首先将商业建筑SCADA系统采集的负荷序列数据进行小波分解；2）应用支持向量机分别针对不同的分量进行预测，获取各分量的预测值，流程如图2所示；3）将各分量对应的预测结果重构得到最终预测值.

图1 商业电力负荷预测流程图 Fig.1 WSVM load forecasting model

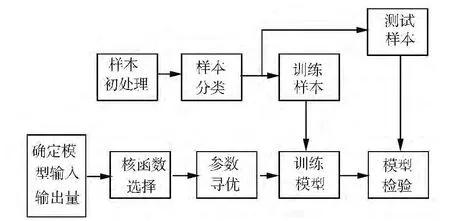
图2 SVM回归建模流程图Fig.2 Flow chart of SVM modeling

4 实例仿真

4.1 小波分解

选用了厦门某商场连续600h的历史负荷数据，采用db3小波基进行小波分解［10］.原始负荷及其分解后的各分量曲线，如图3所示.图3中：a0为原始负荷曲线，由于商场用电高峰时段有较频繁的负荷波动，这给预测结果准确性的提高增加了难度；a3为分解后序列的低频部分，是负荷的基荷部分，a3曲线降低了负荷序列的非平稳性特征，具有明显的日周期性，并保持了原负荷曲线的基本形状，因此，可预测性较强；高频分量d2、d3具有隐含的日周期性；高频分量d1数值较小，表现出较强的随机性.

图3 原始负荷曲线及其小波分解分量Fig.3 Original load curves and its wavelet decomposition components

4.2 各分量进行SVM建模

4.2.1 输入量的选择 对于商业负荷短期预测，其输入量的选择对负荷预测的精度有很大影响，而影响负荷变化的因素多种多样.参考文献［11］，结合商业负荷特性进行分析，影响商业负荷变化的因素主要有：周期性变化因素、相似日因素和天气变化因素.各分量预测模型的输入量，如表1所示.表1中：PLA3（d，h），PLD3（d，h），PLD2（d，h），PLD1（d，h）表示各分量负荷序列在第d天，h时刻的负荷；Tavg表示日平均气温；F表示天气类型；D表示日期类型.

表1 各分量预测模型输入量Tab.1 Input of each components of the forecasting models

4.2.2 模型参数的选择 选择径向基函数作为ε－SVR模型的核函数［12］.研究中发现：惩罚系数C和核宽参数σ的选择对SVM回归估计的精度影响很大，PSO对模型参数进行寻优.粒子群算法具有分布性、自组织性、鲁棒性强等优点，已被成功地应用于函数优化、神经网络等领域［13］.PSO对各层SVM模型参数进行以下寻优步骤.

步骤1初始化得到一群随机粒子（随机解），设其种群规模为20，最大迭代次数为200.

步骤2通过libsvm调用训练数据集，使用当前解作为参数进行回归训练，使用训练精度作为其函数适应值.

步骤3通过对适应值的比较，更新个体最优值pbest和全局最优值gbest.

步骤4更新粒子速度和位置为

式（8），（9）中：w是惯性因子；rand（）代表0到1之间的随机数；xi是粒子位置；vi为粒子速度；pbest和gbest是粒子群搜索到的个体最优值和全局最优值.

步骤5判断是否满足迭代次数，若是则停止迭代，输出最优解；若否，则转至步骤2［14］.

使用粒子群法对各层SVM模型参数寻优之后，分别采用模型对预测日各层分量进行预测，最后重构.将预测日24hPSO和网格寻优结果与误差进行对比，测试结果如表2所示.表2中：EMAPE为平均相对误差.由表2可知：PSO－WSVM的精度高于网格法WSVM.

表2 两种算法得到的最优参数和测试结果Tab.2 Optimal parameters and result of two algorithms

4.3 预测结果分析

选取厦门市某商场380V母线预测日的前4周，共672h的历史负荷数据作为训练样本，提前预测日一日进行连续预测.表3为24h预测误差指标.表3中：平均相对误差为EMAPE；均方误差为EMSE；最大绝对误差为EMAE.从表3中可以看出：PSO－WSVM在EMAPE，EMSE，EMAE上均优于其他两种模型，并能达到实际应用要求.

采用文中方法训练的预测模型，休息日和工作日的预测结果，如图4所示.图4中：9：00至20：00是商场客流量较大的时间段.为了进一步探讨模型性能，同时采用SVM和BP神经网络预测模型进行对比研究.从图4可以看出：3种模型都较好地跟踪了商业负荷的变化趋势，体现了3种预测模型的有效性，PSO－WSVM在负荷曲线突变处和总体的预测精度好于其他方法.

表3 3种预测模型预测误差Tab.3 Error comparison of the three forecasting models

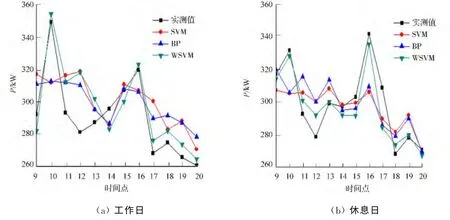
图4 工作日负荷预测结果Fig.4 Forecasting load for workday

5 结论

基于SCADA系统，采用小波变换和SVM相结合的模型对商业电力负荷预测进行了研究.利用小波变换对商业负荷序列进行分解，获得的分量规律性更强.对不同分量建立不同的SVM模型使负荷预测更具针对性.实验结果表明：与网格WSVM和直接使用SVM及BP神经网络的预测结果相比，应用文中方法得到预测精度更高，并且易于推广到其他地区和建筑.

［1］DONG Bing，CAO Cheng，LEE S E.Applying support vector machines to predict building energy consumption in tropical region［J］.Energy and Buildings，2005，37（5）：545－553.

［2］KISSOCK J K.A methodology to measure retrofit energy savings in commercial buildings［D］.Texas：Texas A and M University，1993：32－57.

［3］DHAR A，REDDY T A，CLARIDGE D E.A fourier series model to predict hourly heating and cooling energy use in commercial buildings with outdoor temperature as the only weather variable［J］.Journal of Solar Energy Engineering，1999，121（1）：47－53.

［4］DONG B，LEE S E，SAPAR M H.A holistic utility bill analysis method for baselining whole commercial building energy consumption in Singapore［J］.Energy and Building，2005，37（2）：167－174.

［5］GUILLERMO E.New artificial neural network prediction method for electrical consumption forecasting based on building end－uses［J］.Energy and Building，2011，43（11）：3112－3119.

［6］方瑞明.支持向量机理论及其应用分析［M］.北京：中国电力出版社，2007：15－19.

［7］曾勍炜，徐知海，吴键.基于粒子群优化和支持向量机的电力负荷预测［J］.微电子与计算机，2001，28（1）：147－153.

［8］王红瑞，刘晓红，唐奇，等.基于小波变换的支持向量机水文过程预测［J］.清华大学学报：自然科学版，2010，50（9）：1378－1381.

［9］张华，郁永静，冯志军.基于小波分解与支持向量机的风速预测模型［J］.水利发电学报，2012，31（1）：208－212.

［10］韩勇，李红梅.基于小波分解的支持向量机母线负荷预测［J］.电力自动化设备，2012，32（4）：88－91.

［11］李元诚，方廷健，郑国祥.短期电力负荷预测的小波支持向量机方法研究［J］.中国科学技术大学学报，2003，33（6）：726－732.

［12］梁颖，方瑞明.基于SCADA和支持向量回归的风电机组状态在线评估方法［J］.电力系统自动化，2013，37（14）：8－12.

［13］付宝英，王启志.自适应粒子群优化BP神经网络的变压器故障诊断［J］.华侨大学学报：自然科学版，2013，34（3）：262－266.

［14］路志英，李艳英，陆洁，等.粒子群算法优化RBF－SVM沙尘暴预报模型参数［J］.天津大学学报：学报自然科学版，2008，41（4）：413－418.