基于布尔求差的对数螺旋锥齿轮精确建模

向铁明，顾立志，李鹏，陈维周

（1.华侨大学 机电及自动化学院，福建 厦门361021；2.厦门理工学院 机械与汽车工程学院，福建 厦门361024）

螺旋锥齿轮，又称为弧齿锥齿轮，弧齿伞齿轮，具有传动平稳，噪音低，重合度高的特点，广泛应用于航空航天、机床、船舶及汽车工业［1］.螺旋锥齿轮因齿向线上各点螺旋角不同，造成在制造螺旋锥齿轮时要调整包括刀盘和机床的大量参数，即使这样，也不能做到啮合点螺旋角相等［1］.文献［1－3］提出的对数螺旋锥齿轮，其齿向线是圆锥对数螺旋线，从原理上体现出对数螺旋锥齿轮的优越性，但实际效果及可行性仍需要在设计、CAE分析［4］、加工制造、装配及使用过程中对其进行研究和验证.目前，螺旋锥齿轮的建模日趋成熟.常规螺旋锥齿轮的建模主要有两类方法［5－6］，一类是齿面方程推导为主的拟合建模［7－13］；另一类是虚拟现实的仿真加工建模［14－23］.对数螺旋锥齿轮的建模及研究较少报道，本文根据对数螺旋锥齿轮的形成原理进行精确建模，建模理论误差为零，但在实际建模时，因受计算机建模在数值计算时的截断误差和舍入误差的影响，实际距离误差≤0.1μm.

图1 圆锥对数螺旋线Fig.1 Conical logarithmic spiral line

1 圆锥对数螺旋线方程的推导

在圆锥面上形成的定倾曲线（曲率与挠率之比为常数的曲线）称为圆锥对数螺旋线［24－27］，如图1所示.

设正圆锥面上有动点M，它由M0运动到M1时，在锥面上转过一个τ角.当动点由M1转到M2时，在锥面上变化一个dτ角，则M1点到原点（锥顶）的矢径r也相应增大dr，曲线M1，M2在M2的切线与过M2点的圆锥母线OM2所成角度β，令β为一恒定值，则可推导出圆锥对数螺旋线的矢径方程为

式（1）中：a为圆锥对数螺旋线起点距离锥顶的距离；φ为自变量，表示动点转过的角度在底面的投影；α为圆锥的锥顶半角；β为螺旋角.

把式（1）化成参数方程形式［1－3］，有

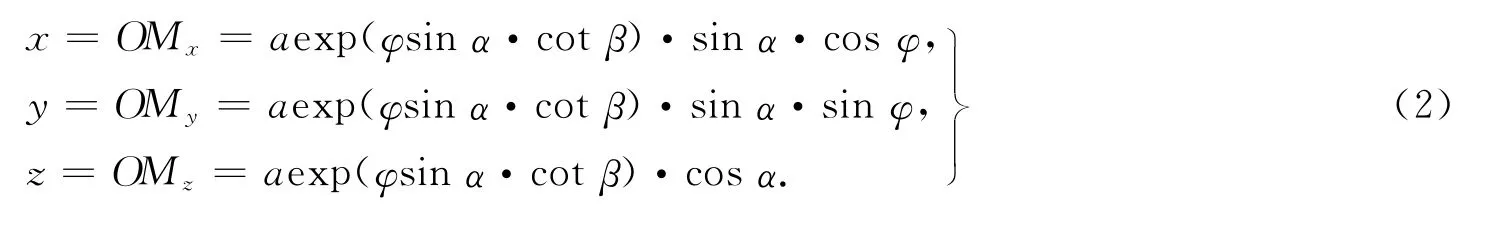
2 对数螺旋锥齿轮精确建模

2.1 对数螺旋锥齿轮精确建模思路

面锥体与齿槽体采用布尔求差的方式，对数螺旋锥齿轮进行三维建模.

2.2 对数螺旋锥齿轮的基本参数

根据某一微型汽车主减速器的格里森制螺旋锥齿轮参数，设计对数螺旋锥齿轮，拟用对数螺旋锥齿轮取代格里森制螺旋锥齿轮，对数螺旋锥齿轮的小齿轮主要参数如下：齿数为9，大端端面模数为4.5 mm，大端分度圆直径为40.5mm，压力角为20°，螺旋角为35°，齿顶高系数为0.85，顶隙系数为0.188.

2.3 齿轮基本曲线的创建

基本曲线包括：齿轮的轴线、面锥母线、节锥母线、根锥母线、基锥母线、背锥母线和前锥母线.根据几何关系可推导出关系式，有

式（3）中：d为大端分度圆直径；da为大端齿顶圆直径；db为大端基圆直径；df为大端齿根圆直径；δ1为小齿轮分锥角；z1为小齿轮齿数；a＊h为齿顶高系数；c＊为顶隙系数.

2.4 齿轮大端和小端的当量齿轮基本圆的创建

大端当量齿轮的基本圆包含大端当量齿轮分度圆，大端当量齿轮齿顶圆，大端当量齿轮基圆和大端当量齿轮齿根圆.其数值计算为

式（4）中：d2为大端当量齿轮分度圆直径；da2为大端当量齿轮齿顶圆直径；db2为大端当量齿轮基圆直径；df2为大端当量齿轮齿根圆直径.

2.5 布尔求差

设A，B分别表示两个实体，由计算几何学及计算机图形学的知识［26］可知，实体A，B进行布尔求差运算表示为

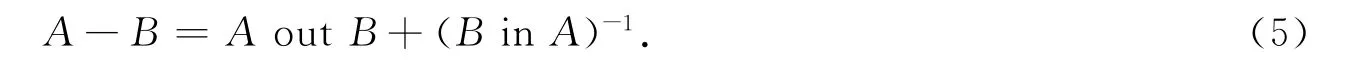
式（5）中：AoutB表示实体A表面处于实体B外的部分；（BinA）－1表示实体B表面在实体A内的部分的补集.

在式（4）所示表达式中，d2，da2，db2，df2的一般形式为无理数，建模如果采用根锥B与轮齿A进行布尔求和，那么计算机在处理无理数问题时，必须对其进行截断.

因截断所产生的误差，造成两者无法相交而运算失败，且误差直接反应在轮齿的工作部分上面，如图2（a）所示.采用面锥D与齿槽实体C进行布尔求差运算方式的建模方法，如图2（b）所示.不仅可以成功完成运算，而且还可以把误差累计到齿槽中去，确保了轮齿工作部分的建模精度.

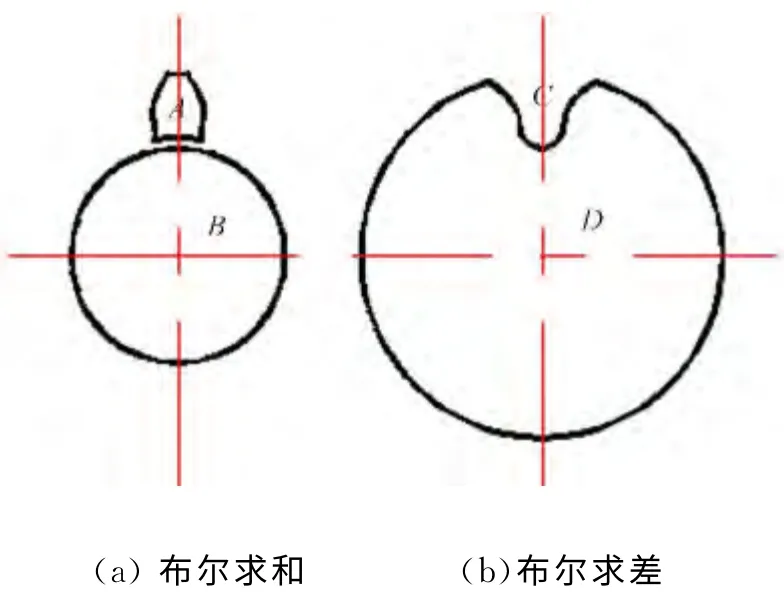
图2 布尔运算Fig.2 Boolean operation

2.6 圆锥对数螺旋线创建

根据UG的表达式功能，分别选择t，logx，logy，logz为规律曲线的内部变量、x坐标、y坐标、z坐标，在分锥上创建圆锥对数螺旋线.r0＝1处作为起始点，半锥角α＝δ1，螺旋角β＝35°，φ角为旋转360°的圆锥对数螺旋线.分锥上的圆锥对数螺旋线即为齿向线，也为精确建模的扫引线.

2.7 大、小端齿轮扫引截面和齿向线的描述与可视化表达

对数螺旋锥齿轮的端面为渐开线齿廓，根据渐开线方程

式（6）中：xt，yt，zt为渐开线坐标；为大端当量基圆半径；θ为渐开线展开角；t为UG系统内部变量，其变化范围0～1.

采用UG的规律曲线功能，绘制大端渐开线，并把渐开线沿着相应的对称中心进行镜像.其中：渐开线与齿根圆通过r2圆弧进行过渡，圆弧半径定义为

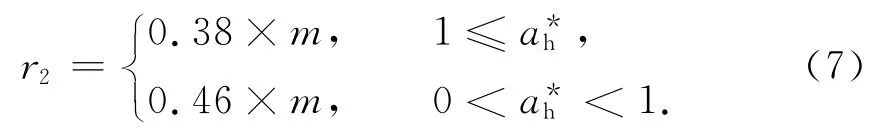
图3 大端齿轮当量渐开线齿槽Fig.3 Equivalent involute space of gear big end

同理，按照小齿轮大端当量渐开线齿槽的建模过程，可以建立小齿轮小端当量渐开线齿槽，如图3所示.

用节锥的上、下两个底面，去截断节2.6所生成的圆锥对数螺旋线，得到结果如图4中实线所示，即为对数螺旋锥齿轮的扫引线（扫掠路径）.

利用UG软件的扫掠功能，选择图4中左、右两端渐开线齿槽为扫掠截面，选择齿向线为扫掠路径，进行扫掠实体建模，得图5所示的一个齿槽实体模型.

图4 扫掠截面与路径 Fig.4 Sweeping section and path

图5 扫掠得出齿槽实体Fig.5 Cogging entity obtained by sweeping

2.8 完整齿轮齿面构建

根据对数螺旋锥齿轮面锥的尺寸，建立面锥的实体模型，并将图5所示的齿槽实体，按照轴线中心进行z1－1个数目的阵列［27］，得到图6所示的效果图.

对图6所示的模型，进行布尔运算，求差，目标体选择面锥体，工具体选择z个齿槽体，进行布尔求差后即得到对数螺旋锥齿轮的小齿轮的三维模型，结果如图7所示.

图6 阵列齿槽 Fig.6 An array of coggings

图7 对数螺旋锥齿轮模型Fig.7 Model of logarithmic spiral bevel gear

3 实体样件加工与测量

为了验证模型的正确性，采用45号钢作为材料，先在普通卧式车床C6140A1上加工出齿坯，再在如图8所示的德玛吉DMU 40monoBLOCK五轴联动数控铣床上进行齿坯的精铣和数控铣削加工（铣齿），得出零件的实体样件，如图9所示.

图8 五轴铣床加工 Fig.8 Five axis milling machine

图9 小齿轮加工样件Fig.9 Sample of pinion

在CONTURA G3三维坐标测量仪上，通过测量大端齿顶圆上的三点，求齿顶圆直径，计算大端齿顶圆直径，测量的数值，如表1所示.

表1 CONTURA G3三维坐标测量数值Tab.1 Three－dimensional coordinate measurement values of CONTURA G3

德玛吉DMU 40monoBLOCK五轴联动数控铣床在某一轴向的线性误差为0.001mm，蔡司CONTURA G3三维坐标测量仪在某一轴向的线性误差为0.001 8mm，使用UG软件建模，进行数值计算时的截断误差和舍入误差为0.1μm＝0.000 1mm.则在某一轴向的累计线性误差为0.002 9mm，在空间的线性误差为

利用蔡司CONTURA G3三维坐标测量，大端齿顶圆直径测量的平均值为47.936 3mm，根据大端齿顶圆的计算值da＝d＋2×a＊h×cosδ1＝47.933 3mm，测量值和计算值之间的误差为

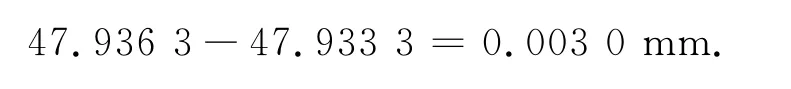
4 结论

1）基于布尔求差的建模方法，采用面锥与齿槽进行布尔求差的方法建模，成功解决了根锥与轮齿求和的方式建模中存在的根锥与轮齿不相交的问题.

2）以齿数为9，模数为4.5mm，压力角为20°，螺旋角为35°的对数螺旋锥齿轮小齿轮为例，对其进行了精确建模，建模理论误差为零，实际距离误差≤0.1μm.

3）采用45号钢作为材料，在普通卧式车床C6140A1上加工出齿坯，在德玛吉DMU 40五轴联动铣床上对所建模型进行了数控铣齿加工，得实体样件.

4）在蔡司CONTURA G3三维坐标测量仪上分三组进行，对大端齿顶圆上最外侧三点进行了三坐标值的测量，大端齿顶圆测量值和计算值之间的误差为0.003 0mm.

［1］李强，闫洪波.对数螺旋锥齿轮啮合理论［M］.北京：冶金工业出版社，2012：3－84.

［2］李强，翁海珊，王国平.对数螺旋线齿锥齿轮齿面的形成及传动原理（Ⅰ）［J］.辽宁工程技术大学学报：自然科学版，2008，27（1）：107－109.

［3］TAN Ru－long，CHEN Bing－kui，PENG Chang－yan，et al.Study on spatial curve meshing and its application for logarithmic spiral bevel gears［J］.Mechanism and Machine Theory，2015，86（4）：172－190.

［4］ANI U，GERD H，PAUL A，et al.Three－dimensional，parallel，finite element simulation of fatigue crack growth in a spiral bevel pinion gear［J］.Engineering Fracture Mechanics，2005，72（8）：1148－1170.

［5］丁撼，阿达依·谢尔亚孜旦，汪永胜.球面渐开线螺旋锥齿轮精确模型设计［J］.机械设计与制造，2014，51（3）：23－26.

［6］丁撼，阿达依·谢尔亚孜旦.弧齿锥齿轮建模的方法及展望［J］.机械设计与制造，2014，51（1）：257－260.

［7］TSAI Y C，HSU W Y.The study on the design of spiral bevel gear sets with circular－arc contact paths and tooth profiles［J］.Mechanism and Machine Theory，2008，43（9）：1158－1174.

［8］JERZY B，ALBERT S，ROMAN P，et al.3Dmodeling of induction hardening of gear wheels［J］.Journal of Computational and Applied Mathematics，2014，270（11）：231－240.

［9］CHEN Shu－hung，FONG Zhang－hua.Study on the cutting time of the hypoid gear tooth flank［J］.Mechanism and Mechine Theory，2015，84（2）：113－124.

［10］LI Hai－tao，WEI Wen－jun，LIU Ping－yi，et al.The kinematic synthesis of involute spiral bevel gears and their tooth contact analysis［J］.Mechanism and Machine Theory，2014，79（9）：141－157.

［11］唐进元，蒲太平，戴进.SGM法加工的螺旋锥齿轮几何建模研究［J］.机械传动，2008，32（1）：43－46，83.

［12］孙玉文，刘宏基，刘健.基于NURBS的自由曲面精确拟合方法研究［J］.机械工程学报，2005，40（3）：10－14.

［13］魏巍，张连洪.计及刀尖圆角和根切的螺旋锥齿轮实体建模［J］.机械设计，2011，28（3）：9－12.

［14］XU Yan－wei，ZHANG Lian－hong，WEI Wei，et al.Virtual machining on monolithic structure spiral bevel gear milling machine［J］.Transactions of the CSAE，2008，24（12）：71－75.

［15］FAN Qi.Computerized modeling and simulation of spiral bevel and hypoid gears manufactured by gleason face hobbing process［J］.Journal of Mechanical Design，2005，128（11）：1315－1327.

［16］LITVIN F L，WANG A G，HANDSCHUH R F.Computerized generation and simulation of meshing and contact of spiral bevel gears with improved geometry［J］.Comput Methods Appl Mech Engrg，1998，158（3）：35－64.

［17］LITVIN F L，FUENTE A，QI Fan，et al.An invariant approach for gear generation with supplemental motions［J］.Mechanism and Machine Theory，2007，42（5）：275－295.

［18］李敬财，王太勇，何改云，等.基于加工方法和啮合理论的螺旋锥齿轮精确实体造型［J］.吉林大学学报：工学版，2008，38（6）：1315－1319.

［19］房怀英，洪尚任，杨建红.克林贝格螺旋锥齿轮的建模与仿真［J］.华侨大学学报：自然科学版，2004，25（1）：67－70.

［20］CHEN Hai－feng，TANG Jin－yuan，ZHOU Wei.Modeling and predicting of surface roughness for generating grinding gear［J］.Journal of Materials Processing Technology，2013，213（5）：717－721.

［21］JAVED H S，NEELESH K J.Modeling of material removal rate and surface roughness in finishing of bevel gears by electrochemical honing process［J］.Journal of Materials Processing Technology，2014，214（2）：200－209.

［22］LITVIN F L，FUENTES A，HAYASAKA K.Design，manufacture，stress analysis，and experimental tests of low noise high endurance spiral bevel gears［J］.Mechanism and Machine Theory，2006，41（1）：83－118.

［23］SIMON V.Computer simulation of tooth contact analysis of mismatched spiral bevel gears［J］.Mechanism and Machine Theory，2007，42（3）：365－381.

［24］CHRISTOPH B，GERALD F.Approximation of logarithmic spirals［J］.Computer Aided Geometric Design，1997，14（1）：515－532.

［25］JOEL T A，MICHELE G，JEAN P V.Designing and manufacturing spiral bevel gears using 5－axis computer numerical control（CNC）milling machines［J］.Journal of Mechanical Design，2013，135（2）：024502（1－6）.

［26］陈学工，杨兰，黄伟，等.三维网格模型的布尔运算方法［J］.计算机应用，2011，32（6）：1543－1545，1584.

［27］JIN Xiang－yuan，ZHANG Tie－feng，YANG Han－lin.Research on the 3Dsolid modeling of high efficient gear tooth based on proE［J］.Procedia Engineering，2012，29（2）：2990－2994.