基于Modelica 的磁流变制动器多领域建模与仿真*

李志华，原龙昊，龚友平

(杭州电子科技大学 机械工程学院，浙江 杭州 310018)

0 引言

随着电动汽车的发展，一种新型线控制动器—磁流变制动器逐渐得到人们的重视与研究。相比传统的液压制动器，它能够减少制动滞后时间、缩短制动距离、简化制动系统结构、方便地集成各种新型控制技术，从而极大地提高汽车制动性能，有效保障驾乘人员的生命财产安全，具有广阔的工程化应用前景和巨大的商业价值［1-4］。

Kerem 等［5］探讨了磁流变制动器设计中应考虑的一些因素，如磁路设计、材料选择、磁流变液选择、密封、粘性力矩、电流密度等。Edward［6］和Younis［7］分别建立了以最大化制动力矩和最小化重量为目标的优化设计模型，并分别采用模拟退火法和全局优化算法SEUMRE 进行优化求解。Edward 等［8］用有限元法设计了双盘式磁流变制动器，并在四分之一车模型下分析了制动性能。国内汪建晓等［9］设计并制作了一种小型圆盘式磁流变制动器。宋宇［10］设计了一种复合叶轮式磁流变制动器。本课题组［11-12］分析并优化设计了一款用于微型汽车的圆筒式磁流变制动器。

尽管国内外对磁流变制动器开展了一些研究，但大多数都将结构设计与磁路设计分割开来。实际上，由于磁流变制动器存在着复杂的机-电-液-磁等多领域耦合问题，如果采用不同领域工具，对磁流变制动器分属于不同领域的各个部分，进行分别建模，然后集成，则势必会因系统耦合性差、集成度不高而造成仿真精度和效率等方面的问题。如果采用多领域统一建模的方法，就能够在一个系统化的理论基础上采用统一的工具平台，对磁流变制动器进行统一建模，进而进行仿真分析、性能评价与优化设计，从而克服采用工具集成的方法所带来的问题。

因此，本研究基于多领域统一建模理论及Modelica 语言［13］，使用MWorks 平台［14］，对磁流变制动器进行多领域统一建模与仿真，然后进行实物样机实验。

1 磁流变制动器工作原理

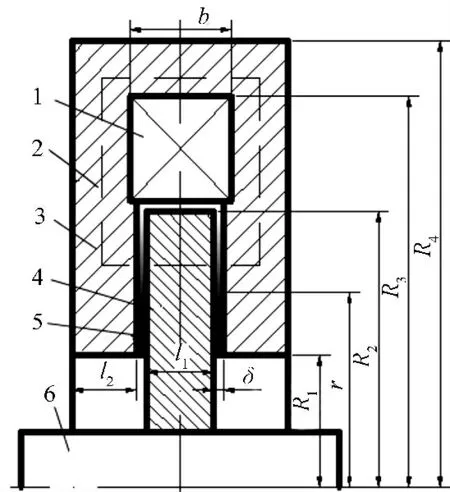
图1 磁流变制动器简图

磁流变制动器简图如图1 所示。制动器主要由制动盘(转子)和外壳(定子)两部分组成，二者间的间隙内充满磁流变液。外壳材料采用导磁率高的20 钢，制动盘采用电工纯铁DT4。在没有外加磁场时，磁流变液表现为牛顿流体，转子可在磁流变液中自由转动，此时仅有少量的流体粘性力矩。当励磁线圈通电后，磁流变液在磁场作用下发生流变效应，转变为类固体状态，从而对制动盘产生剪切制动力矩。由于磁流变液的这种变化是可逆的，而且磁场强度越大，磁流变液产生的屈服应力也越大，通过调节励磁线圈的电流，就可以调节制动力矩的大小。

2 磁流变制动器多领域统一建模

2.1 磁场模型

磁流变制动器的磁场模型是一个涉及结构参数、材料磁导率参数和电磁参数的多领域耦合模型，它反映出电流与磁场强度或磁感应强度的关系。

如图1 所示，封闭虚线表示磁通的走向(即磁路):先沿制动器的轴向穿过制动盘和磁流变液，然后沿制动器的外壳侧面和顶面回到制动盘。根据安培环路定律和磁路欧姆定律知:

式中:φ—磁通量;n—励磁线圈匝数;I—励磁电流;Rm—磁路中的总磁阻，它可由下式求得:

式中:μ—磁导率，S—磁路的横截面积，l—磁路的长度。

根据图1 所示的结构及材料特性，磁路中各部分的磁阻分别为:

(1)制动盘:

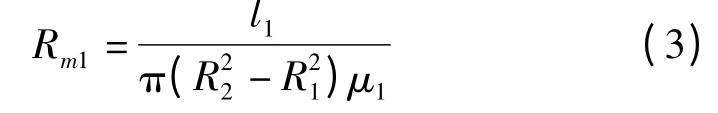
(2)磁流变液:

(3)外壳侧面(水平方向):

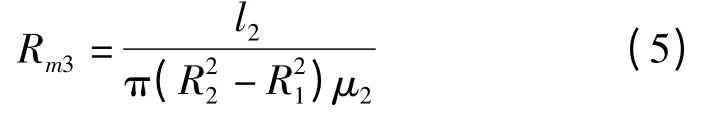
(4)外壳侧面(竖直方向):

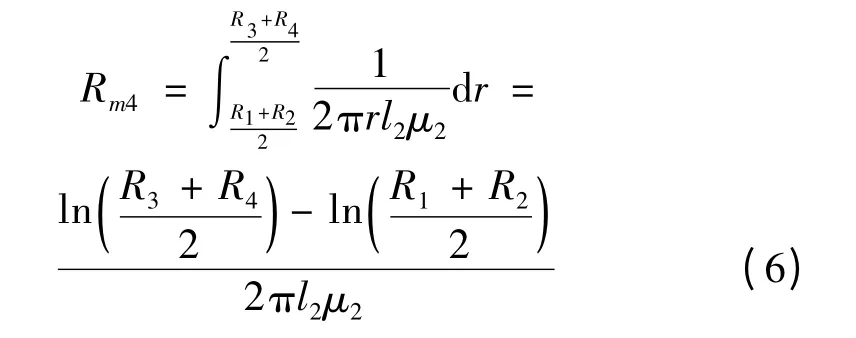
(5)外壳顶面:

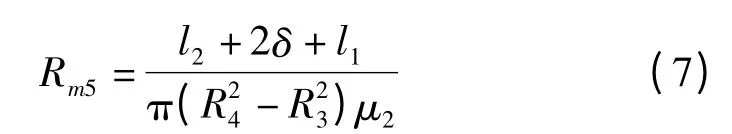
因此，磁路中的总磁阻:

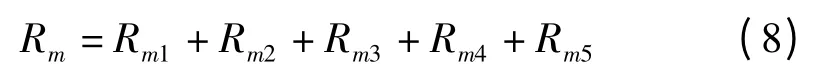
式中:μ1，μ2—制动盘和外壳的磁导率;μm—磁流变液的磁导率;R1，R2—制动盘的最小工作半径和最大工作半径;R3—线圈最大半径;R4—制动器外径;l1—制动盘厚度;l2—制动器外壳厚度。

由于磁路设计的目的是使通过磁流变液的磁通量最大，以获得最大的制动力矩。而通过磁流变液的磁通量为:

式中:B—磁流变液处的磁感应强度，S—磁流变液处的磁路横截面积。

将式(9)代入式(1)，并整理得:

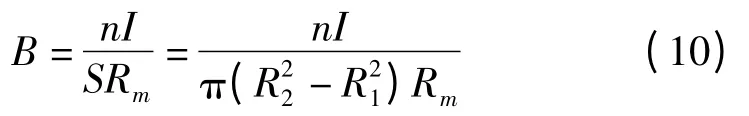
根据磁流变液的B-H 曲线(这里选用Lord 公司的MRF-132DG 型磁流变液［15］B-H 曲线，该曲线如图2 所示)，即可由磁感应强度B 的值，得到磁场强度H 的值。

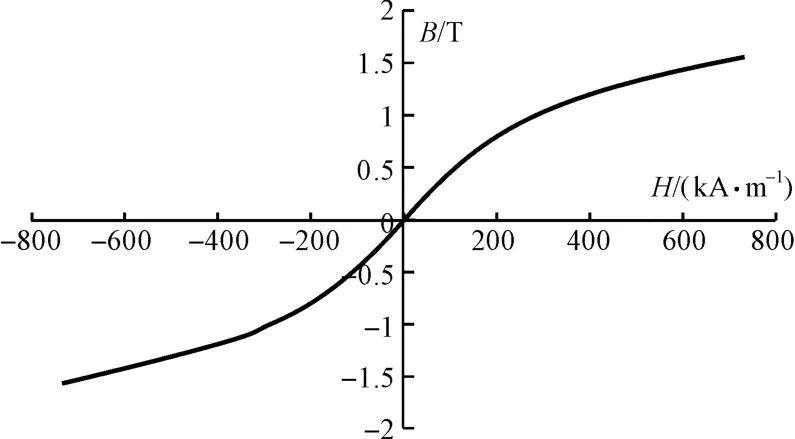
图2 MRF-132DG 型磁流变液的B-H 曲线

根据以上分析，基于Modelica 语言，本研究使用MWorks 平台，得到的磁流变制动器的Modelica 磁场模型如图3 所示。

图3 磁流变制动器的Modelica 磁场模型

2.2 制动力矩模型

制动力矩模型是一个涉及结构参数、磁流变液参数和磁场强度的多领域耦合模型，它反映出磁场强度与制动力矩的关系。

如图1 所示，制动器的工作区域为半径R1～R2的制动盘的两圆环表面，在任意半径r 处取一微环，其面积为ds=2πrdr，则产生的作用力为:dF=τds，τ 为磁流变液的剪切应力，从而传递的微力矩为:

可得制动盘的单侧力矩为:

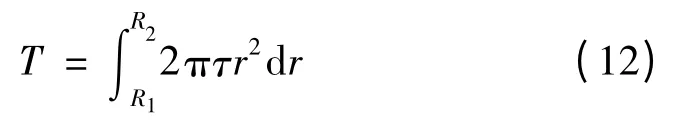
假设磁流变液为不可压缩的Bingham 流体，且仅在与转轴垂直方向进行层流运动。由Bingham 塑性模型可知:

式中:τy—磁流变液的动态屈服应力，η—磁流变液的粘度，—磁流变液的剪应变率。

由于磁流变液在径向和轴向均不流动，其流速仅是半径的函数，则有=ω/δr(其中:ω—转轴转速，δ—制动盘与外壳之间的工作间隙)。

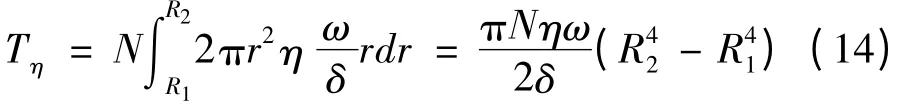
当有外加磁场时，磁流变液表现为Bingham 流体，此时τ=τy=kHβ，则产生的剪切制动力矩TM为:

式中:N—制动盘的工作面数，这里取2;k，β，η—磁流变液的参数，对于MRF-132DG 磁流变液，k=0.24，β=1，η=0.09 Pa·s。

因此，磁流变制动器产生的总制动力矩为:

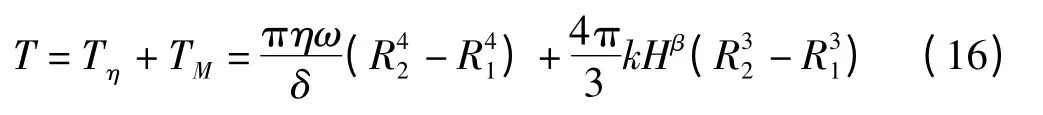
根据以上分析，得到的磁流变制动器的Modelica制动力矩模型如图4 所示。

3 仿真结果分析

从制动力矩模型可以看出，影响磁流变制动器制动性能的主要因素有:结构参数、磁路参数、材料特性、工作间隙、转轴转速和励磁电流等。通过改变各参数值即可仿真得到磁流变制动器在不同情况下的性能，如图(5～7)所示。

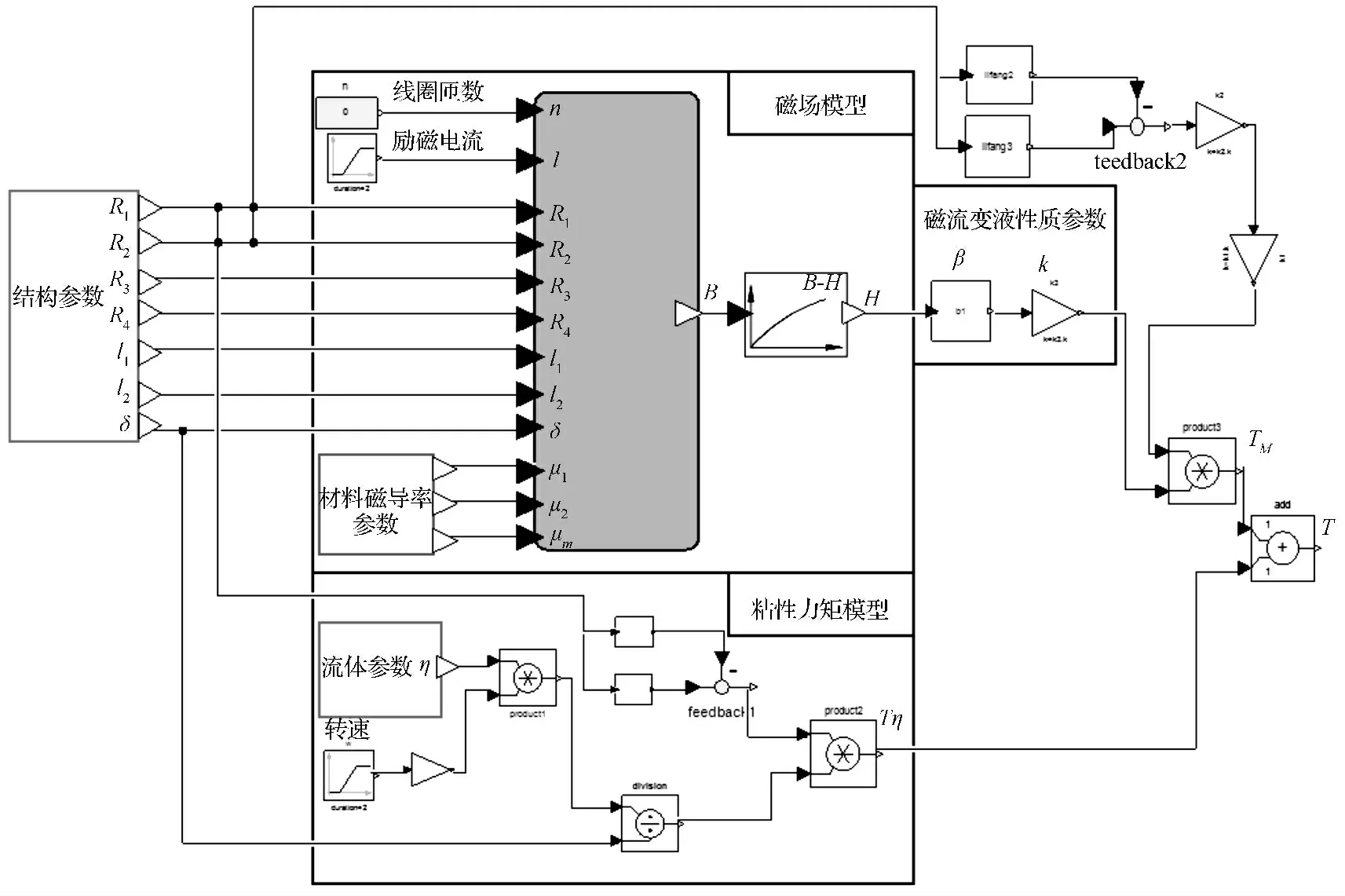
图4 磁流变制动器的Modelica 制动力矩模型

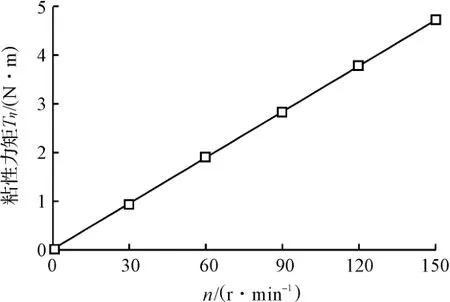
图5 不同转速下的Tη值

图6 不同电流下的T 值

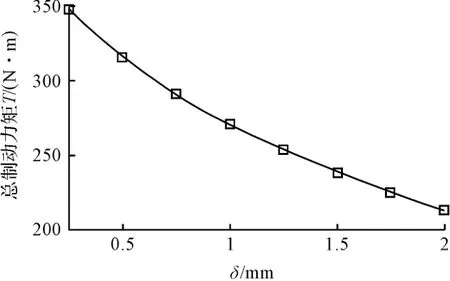
图7 不同工作间隙下的T 值

不同转速下的Tη值如图5 所示。在其他参数固定且无磁场作用的情况下，粘性力矩Tη与转轴转速ω呈线性关系，转速越大，粘性力矩也越大。但粘性力矩只占总制动力矩的很小部分，如图6 所示。图6 中，不同转速下的3 根曲线几乎重合，其细微差别仅是受粘性力矩的影响。因此，磁流变制动器的总制动力矩主要是由剪切制动力矩TM提供，而剪切制动力矩随着电流的增大而增大。因此，通过调节励磁线圈的电流，就可以调节制动力矩的大小。

工作间隙δ 不仅影响磁场强度H 从而改变TM，而且还直接影响Tη。不同工作间隙下的T 值如图7 所示。工作间隙越小，产生的总制动力矩越大。但由于考虑到制造和装配的困难，以及磁流变的效应，工作间隙不可过小，通常取值0.25 mm～2 mm。

为了进一步验证所建模型的正确性，本课题组设计制造了一款用于微型汽车的单盘式磁流变制动器，其参数为:R4=150 mm，R3=137 mm，R2=130 mm，R1=25 mm，l1=11 mm，l2=9 mm，δ=1 mm，b=13 mm，线圈300 匝。选用的磁流变液是Lord 公司的MRF-132DG，搭建的制动器性能测试平台如图8 所示。

首先让电机稳定运行到额定转速后，经减速器减速至95 r/min，然后接通电磁离合器，并记录磁流变制动器在输入电流为0 时的输出力矩。通过调节直流稳压电源使得制动器的输入电流分别为0.2 A、0.4 A、……、2.0 A(以0.2 A 为间隔递增)，并分别记录各个电流值下的输出力矩。实验结果如图9 所示。

图8 实验测试平台

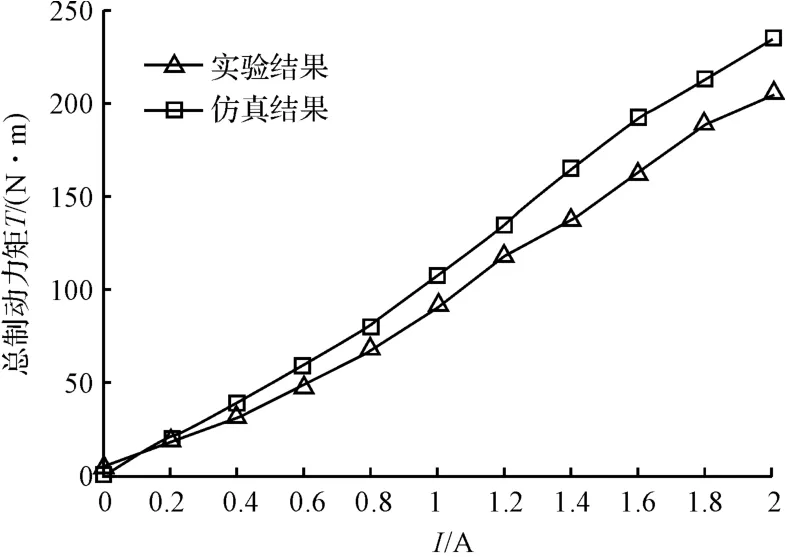
图9 实验结果与仿真结果的对比

由图9 可知，实验结果与仿真结果的曲线走势基本一致，但实际测得值比理论值要小些，这是因为实际中存在的漏磁、制动器温升、制动器加工装配误差等因素都会造成实际值比理论值小。此外，从图9 中还可以看出，当电流为2 A 时，磁流变制动器的实际输出力矩为204.7 N·m，满足微型汽车CV6 的200 N·m 的使用要求，而此时输入电流没有超过励磁线圈的许用值。

4 结束语

磁流变制动器是一种新型线控制动器，属于典型的多领域耦合的复杂物理系统。已有的工作都是对磁流变制动器的结构、磁场和控制等各领域进行单独研究，并采用传统的单领域工具，如ANSYS和Matlab等，进行仿真分析。本研究基于Modelica/MWorks 平台，采用多领域统一建模方法，充分考虑各领域的耦合关系，对磁流变制动器所涉及到的结构、电磁场、机械动力学和流体等多个学科领域，进行多领域统一建模。

实验结果和仿真结果表明，本研究所建立的多领域统一模型是正确的，并可作为模型库用于磁流变制动器后续的优化设计和产品开发。

［1］LI W H，DU H.Design and experimental evaluation of a magnetorheological brake［J］.Advanced Manufacturing Technology，2003，21(7):508-515.

［2］NAM Y J，MOON Y J，PARK M K.Performance improvement of a rotary MR fluid actuator based on electromagnetic design［J］.Journal of Intelligent Material Systems and Structures，2008，19(6):695-705.

［3］ROSSA C，JAEGY A，MICAELLI A，et al.Development of a multilayered wide-ranged torque magnetorheological brake［J］.Smart Materials and Structures，2014，23(2):1-11.

［4］ROSSA C，JAEGY A，LOZADA J，et al.Design considerations for magnetorheological brakes［J］.IEEE/ASME Transactions on Mechatronics，2014，19(5):1669-1680.

［5］KEREM K，EDWARD J P，AFZAL S.Design considerations for an automotive magnetorheological brake［J］.Mechatronics，2008，18(8):434-447.

［6］EDWARD J P，LUIS F L，AFZAL S.Multidisciplinary design optimization of an automotive magnetorheological brake design［J］.Computers and Structures，2008，86(3-5):207-216.

［7］YOUNIS A，KARAKOC K，DONG Z，et al.Application of SEUMRE global optimization algorithm in automotive magnetorheological brake design［J］.Structural and Multidisciplinary Optimization，2011，44(6):761-772.

［8］EDWARD J P，DILIAN S，LUIS F L，et al.A performance evaluation of an automotive magneto-rheological brake design with a sliding mode controller［J］.Mechatronics，2006，16(7):405-416.

［9］汪建晓，孟 光，任小平，等.磁流变液制动器的设计与制动性能测试［J］.机械科学与技术，2003，22(3):406-407，414.

［10］宋 宇.磁流变液ABS 制动器结构研究与性能仿真［D］.哈尔滨:东北林业大学交通学院，2011.

［11］李志华，朱丰友，郭林超.圆筒式磁流变制动器结构设计［J］.机械设计与研究，2008，24(6):49-51.

［12］李志华，林 阳，朱丰友，等.圆筒式磁流变制动器结构与磁路耦合的优化设计［J］.工程设计学报，2009，16(4):261-265.

［13］赵建军，丁建完，周凡利，等.Modelica 语言及其多领域统一建模与仿真机理［J］.系统仿真学报，2006，18(Z2):570-573.

［14］吴义忠，吴民峰，陈立平.基于Modelica 语言的复杂机械系统统一建模平台研究［J］.中国机械工程，2006，17(22):2391-2396.

［15］LORD Corporation.MRF-132DG Magneto-Rheological Fluid［EB/OL］.［2009-03-01］.http://www.lordfulfillment.com/upload/DS7015.pdf