两个（2+1）维长水波方程组的精确解

詹 雨，呼家源

（1.河套学院发展规划与教育评价中心，内蒙古巴彦淖尔 015000；2.河套学院理学系，内蒙古巴彦淖尔 015000）

两个（2+1）维长水波方程组的精确解

詹 雨1，呼家源2

（1.河套学院发展规划与教育评价中心，内蒙古巴彦淖尔 015000；2.河套学院理学系，内蒙古巴彦淖尔 015000）

以齐次平衡原则为基础，利用计算软件Mathematica对（2+1）维耗散长水波方程组和（2+1）维色散长水波方程组的精确解进行研究，并对拟解的形式加以推广，从而得到两个长水波方程组的新的精确解，其解的结构和性质与相关文献的结论比较起来更加丰富全面。

长水波方程组；精确解；齐次平衡法

［DOI］10.3969/j.issn.1672-2345.2015.12.001

非线性偏微分方程的精确解问题一直是非线性科学研究的热点问题之一〔1〕，这些精确解可以准确描述所对应的非线性现象，因此很多学者热衷于寻找典型的非线性偏微分方程的精确解。文〔2〕应用齐次平衡法获得了（2+1）维色散长水波方程组的Bücklund变换和一个线性偏微分方程，在此基础上获得了（2+1）-维色散长波方程的多孤子解和单孤子解；文〔3〕利用一般多线性分离变量法对（2+1）维耗散长水波方程组进行求解，得到了含有任意函数的一般多线性分离变量解；文〔4〕利用拓展（G′/G）-展开法，引入非行波变换，得到了（2+1）-维耗散长水波方程的带独立变量任意函数的非行波解。本文利用齐次平衡原则〔5-8〕，通过拟解的4种不同推广形式，对这两个长水波方程组进行了精确求解，得到了更为丰富的含有任意函数的精确解。

1 齐次平衡法简述

下面先以一个未知函数、两个自变量的情形为例，概述齐次平衡法的基本思想和步骤，对于多个未知函数和自变量的方程组，表述方法类似。

已知非线性偏微分方程

其中P是变元u，ux，ut，uxx，uxt，utt，L的多项式。函数φ=φ（x，t）满足下面的条件时，称为是方程（1）的拟解：

如果存在单变元的函数 f=f（φ），使得 f（φ）关于x，t的一些偏导数的适当的线性组合，精确地满足（1），

即

其中 f~（φ）是关于x和t的低于m+n阶偏导数的适当的线性组合；也可将上式改写为

其中～φ（x，t）是以各种偏导数为变元的低于m+n次的一个多项式，可以使得（1）成立。

式（2）及（3）中的非负整数m，n，单变元函数 f（φ）以及函数φ=φ（x，t）都待定，可通过下述步骤得以确定：

步骤一 使最高阶偏导数项和非线性项中包含的关于φ（x，t）的偏导数的最高幂次相等，确定m和n的值，一般情况下是整数。

步骤二 合并φ（x，t）的偏导数的最高幂次项，令其系数为零，得到 f（φ）满足的常微分方程，解之可得f=f（φ），通常是对数函数 f=rlnφ。

步骤三 用 f（φ）高阶导数替换 f（φ）的各阶导数的非线性项，合并 f（φ）的各阶导数项后，令其系数为零，得到φ=φ（x，t）的齐次型的超定偏微分方程组

通常可以设φ=φ（x，t）有下面形式解

其中m，n为待定常数。

本文在（2+1）维方程组的情形下，对φ=φ（x，y，t）的形式进行了以下推广：

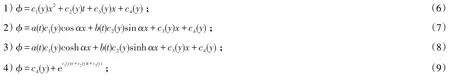
其中α及a（t），b（t），c1（y），c2（y），c3（y），c4（y）为待定常数和函数。

把φ代入H（φ）=0，可得待定常数满足的代数方程组和待定函数满足的微分方程组，它们一般都是可以求解的。

步骤四 若前3步的解答是肯定的，将结果代入（3），即可得到（1）的精确解。

2 （2+1）维耗散长水波方程组的精确解

对于（2+1）维耗散长水波方程组

先利用齐次平衡原则求其行波解。设

平衡方程（10）与（11）的最高偏导数项uxx与非线性项（uv）x，（v2）xy，得m1=1，n1=1，l1=0，m2=1，n2=0，l2=0，因而可设方程组具有以下形式的解

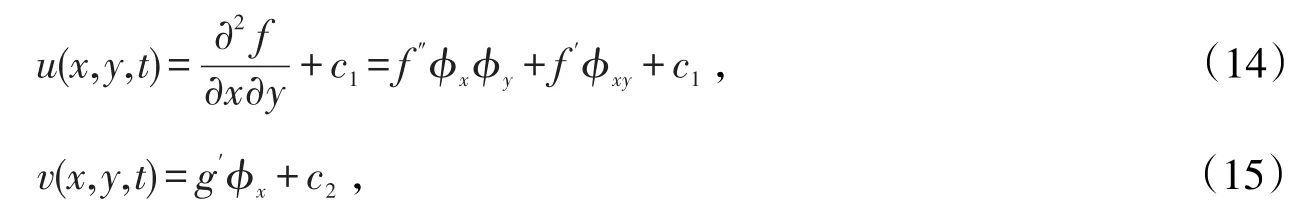
其中c1，c2为常数，φ=φ（x，y，t）是关于x，y，t的函数。

将（14）、（15）代入方程（10）、（11），整理后得到

令（16）、（17）式中φ3xφy的系数为零，得到常微分方程

和

当g=f时，设方程（18）和（19）有形式解：f=rlnφ，r为待定常数，代入方程（18）或（19）后，可解得r=1，即

同时还可以求得下列关系式：

将（18）、（19）、（20）代入方程（16）和（17）的左端，整理后得到方程

和

令方程（22）和（23）中 f的各阶导数的系数为零，得到方程组

假设

其中m，n，l为待定常数，ξ0为任意常数，将（24）代入（25）中，化简后可得待定常数m，n，l满足的方程组

解得

将（20）、（25）、（27）代入（14）、（15），得（2+1）维耗散长水波方程组的第一组精确解（行波解）

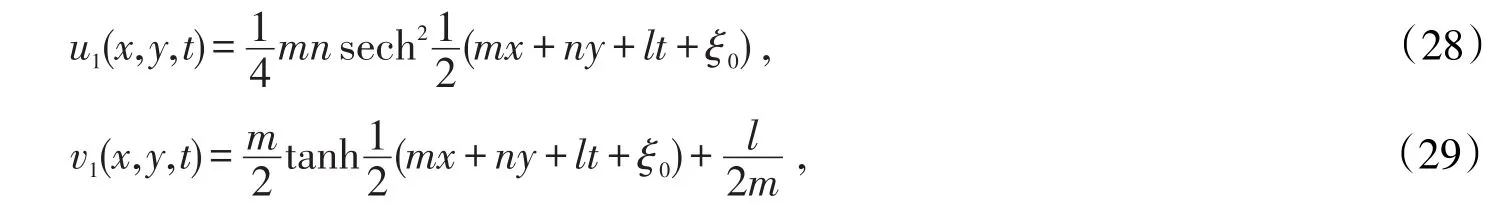
其中m，n，l和ξ0均为任意常数。

设（14）和（15）中的常数c1=c2=0，经过与上面相同的过程，可以得到φ的各阶偏导数所满足的关系式

显然，当

时，（30）式成立。

1）设 φ=c1（y）x2+c2（y）t+c3（y）x+c4（y）（其中 c1（y），c2（y），c3（y），c4（y）为待定函数），代入（31）式，可解得c2（y）=2c1（y），因而

代入（14）和（15），可得（2+1）维耗散长水波方程组的第二组精确解

其中c1（y），c3（y），c4（y）是变量y的任意可导函数。

2）设φ=a（t）c1（y）cosαx+b（t）c2（y）sinαx+c3（y）x+c4（y）（其中α为待定常数，a（t），b（t），c1（y），c2（y），c3（y），c4（y）为待定函数），代入（31）式，可解得a（t）=b（t）=e-α2t，因而

代入（14）和（15），可得（2+1）维耗散长水波方程组的第三组精确解

其中α是任意实数，c1（y），c2（y），c3（y），c4（y）是变量y的任意可导函数。

3）设φ=a（t）c1（y）coshαx+b（t）c2（y）sinhαx+c3（y）x+c4（y）（α为待定常数，a（t），b（t），c1（y），c2（y），c3（y），c4（y）为待定函数），代入（31）式，可解得a（t）=b（t）=eα2t，因而

代入（14）和（15），可得（2+1）维耗散长水波方程组的第四组精确解

其中α是任意实数，c1（y），c2（y），c3（y），c4（y）是变量y的任意可导函数。

4）设φ=c4（y）+ec1（y）x+c2（y）t+c3（y）（其中c1（y），c2（y），c3（y），c4（y）为待定函数），代入（31）式，可解得c2（y）=c21（y），因而

代入（14）和（15），可得（2+1）维耗散长水波方程组的第五组精确解

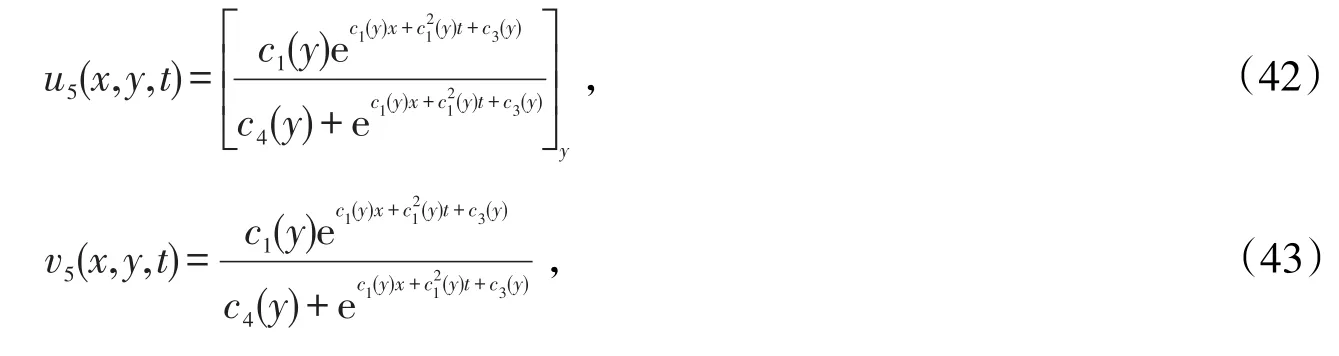
其中c1（y），c3（y），c4（y）是变量y的任意可导函数。

第二至五组精确解为非行波解。

3 （2+1）维色散长水波方程组的精确解

对于（2+1）维色散长水波方程组

经过与（2+1）维耗散长水波方程组相似的计算过程，也可以得到以下4种形式的精确解。

1）第一组精确解为

其中c1（y），c3（y），c4（y）是变量y的任意可导函数。

2）第二组精确解为

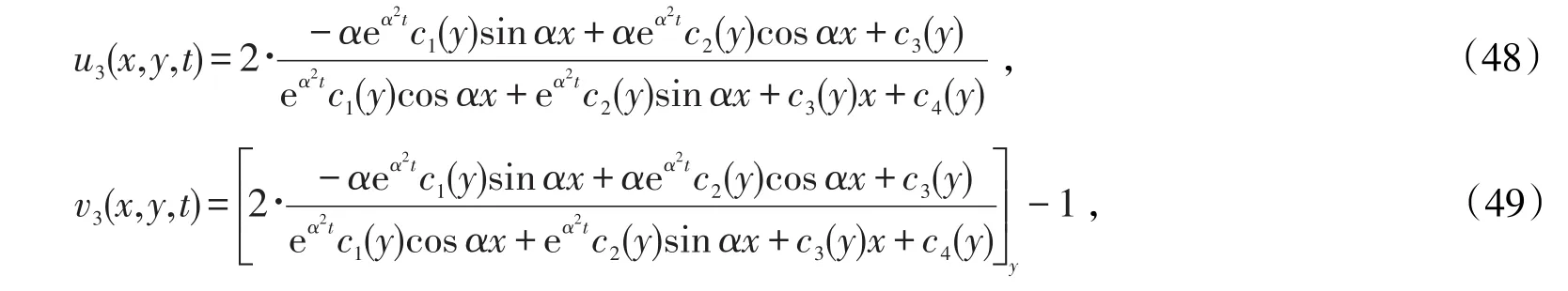
其中α，d是任意实数，c1（y），c2（y），c3（y）是变量y的任意可导函数。

3）第三组精确解为

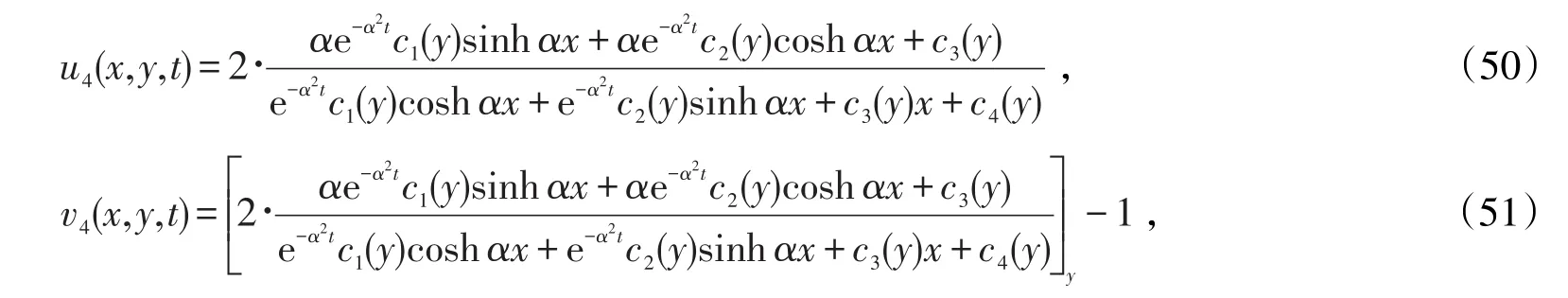
其中α是任意实数，c1（y），c2（y），c3（y），c4（y）是变量y的任意可导函数。

4）第四组精确解为

其中c1（y），c3（y），c4（y）是变量y的任意可导函数。

这4组精确解均为非行波解。

4 结语

在利用齐次平衡原则求解（2+1）维耗散长水波方程组和（2+1）维色散长水波方程组时，对拟解的形式加以推广，获得了一些包含任意函数的非行波解，通过选取适当的函数，可以得到很丰富的孤子结构，使其解系更加丰富了，为进一步研究这两个方程组所反映的非线性现象提供了基础。

〔1〕套格图桑.论非线性发展方程求解中辅助方程法的历史演进〔M〕.北京：中央民族大学出版社，2012.

〔2〕夏铁成，张鸿庆.（2+1）维扩散长水波方程的衰变解和其它精确解〔J〕.甘肃工业大学学报，2003，29（1）：124-127.

〔3〕包志华，斯仁道尔吉，包来友.（2+1）维耗散长水波方程的一般多线性分离变量解〔J〕.内蒙古师范大学学报（自然科学汉文版），2010，39（1）：18-21.

〔4〕何晓莹，赵展辉.（2+1）-维耗散长水波方程的非行波解〔J〕.西北师范大学学报（自然科学版），2013，49（5）：43-46.

〔5〕WANG Mingliang.The Solitary wave solutions for variant Boussinesq equations〔J〕.J Physics Letters A，1995（199）：168-172.

〔6〕王明亮，李志斌，周宇斌.齐次平衡原则及其应用〔J〕.兰州大学学报（自然科学版），1999（3）：8-15.

〔7〕李志斌.非线性数学物理方程的行波解〔M〕.北京：科学出版社，2008.

〔8〕郭玉翠.非线性偏微分方程引论〔M〕.北京：清华大学出版社，2008.

Exact Solutions of Two（2+1）-dimensional Long Water Wave Equations

Zhan Yu1，Hu Jiayuan2
（1.Center of Development Planning and Education Evaluation，Hetao College，Bayannur，Inner Mongolia 015000，China；2.Department of Science，Hetao College，Bayannur，Inner Mongolia 015000，China）

On the basis of the homogeneous balance principle，the exact solutions of（2+1）-dimensional dissipative long wave equation and the（2+1）-dimensional dispersive long wave equation are studied with the aid of Mathematica software.Moreover，by generalizing the form of quasi-solution，new exact solutions of two long wave equations are obtained，and the structure and properties of these solutions are more comprehensive than the conclusions in relevant literature.

long wave equations；exact solution；homogeneous balance method

O156.4

A

1672-2345（2015）12-0001-06

（责任编辑 袁 霞）

内蒙古高等学校科学研究自然科学一般项目（NJZY265）

2015-10-27

詹雨，副教授，主要从事符号计算及应用研究.