影响精确界定我国酸雨区空间分布的因素探讨

胡炳清，易 鹏，段 宁，赵德刚，赵金民，程 轲（.中国环境科学研究院，北京 000；.河南师范大学环境学院，黄淮水环境与污染防治教育部重点实验室，河南 新乡 453007）

影响精确界定我国酸雨区空间分布的因素探讨

胡炳清1*，易 鹏1，段 宁1，赵德刚1，赵金民1，程 轲2（1.中国环境科学研究院，北京 100012；2.河南师范大学环境学院，黄淮水环境与污染防治教育部重点实验室，河南 新乡 453007）

利用酸雨监测网的实测数据对影响精确界定我国酸雨区空间分布的因素进行了深入分析，结果表明：首要影响因素是酸雨监测网的站点数量及其空间分布，可导致在同一插值与地统计方法下所获得的酸雨区的分布存在较大差异；其次是选择正确、合适的空间插值方法及其相应参数的设置，反距离加权（IDW）插值法的重酸雨区分布比克里格（Kriging）插值法多而广；最后是精确的面积比测算方法，网格法计算的酸雨区面积比小于等值面法.建议我国酸雨监测网建设应优先在西藏、内蒙古北部及西部等地区布点，进行酸雨区空间分析时应采用多种插值方法进行比较与分析评估，确保在现有酸雨监测网的基础上获得精确、可靠的酸雨区空间分布.

酸雨区；空间分析；地统计分析；插值效果评价

酸雨，因其危害民众健康、腐蚀文物古迹、破坏生态系统，已成为当今世界上备受关注的重大环境问题之一［1-4］.2013年中国环境状况公报显示，我国473个监测降水的城市中，出现酸雨的城市比例为44.4%，酸雨频率在25%以上的城市占比27.5%，以上公布的酸雨区面积比例是按照环保部门的酸雨监测网的年均pH值通过一定的空间插值方法得到的，这与其它酸雨监测网获得的结果存在差异，甚至有较大的不同［5］.而我国酸雨区的空间分布是客观存在的，如何更加科学、客观地反映我国酸雨区的空间分布显得尤为重要.

1 酸雨监测网站点数量及空间分布

1.1 监测网站点数量影响

影响精确界定我国酸雨区空间分布的首要因素是酸雨监测网布点，主要包括酸雨监测网布点的数量及其空间分布.如果不同的酸雨监测网在酸雨监测（尤其是降水pH值测量）上所采用的测量方法是统一的，造成不同酸雨监测网获得的酸雨区分布与面积比不一致的主要原因就是酸雨监测网的布点［6-7］.由于不同酸雨监测网在测量方法和质量控制与保证上可能存在差异，无法直接用不同酸雨监测网的布点加以比较说明.为此，在同一酸雨监测网布点下采用随机函数选择酸雨监测站点的方法，分别从915个监测站点随机获得了200、400、600和800等4种不同样本数的酸雨监测数据集，监测站点的空间分布见图1.

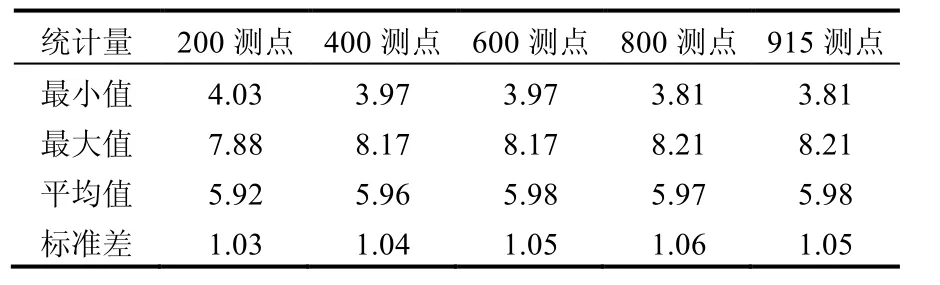
表1 不同随机选择样本与全样本数据集的统计量Table 1 The statistics of different random selected samples and full samples datasets

4种样本与全样本监测数据的统计结果见表1，4种随机样本的降水pH值的频数分布如图2.从图2可见，随着样本数的增加，频数分布集中程度增加，并且呈现双峰的态势，800个监测点的样本已非常接近于915个监测点的全样本.

图1 4种随机抽样下酸雨监测点和年均pH值的空间分布Fig.1 Spatial distribution of four random selected acid rain monitoring sites and annual pH value

将这4个样本与全样本采用统一的空间插值和地统计分析方法进行数据处理和分析（表2），结果表明重酸雨区与酸雨区的面积在不同布点下存在较大的差异，重酸雨区比例最大的为800监测点样本，最小的为200点样本，而轻酸雨区和酸雨区比例最大的为200监测点样本，最小的为800点样本.

图2 不同随机样本降水pH值的频数分布Fig.2 Frequency distribution of pH value of precipitation of different random selected samples

表2 不同随机选择样本下酸雨区面积比（%）Table 2 Area ratio of acid rain area of different random selected samples（%）

2008年A酸雨监测网的样本数为915个，B酸雨监测网的样本数为157个，其酸雨监测点位分布见图3.B网pH平均值为5.36，最小值为4.06，最大值为8.02，标准差为1.02，与A网（表1）相比，平均值小10%，频数分布表现为正偏态，即多数监测点位的pH值位于平均值右侧.A网监测点位多，主要位于城区，B网监测点位少，主要位于郊区.

1.2 监测网站点空间分布影响

反距离加权法是以插值点与样本点之间的距离为权重的插值方法，插值点越近的样本点被赋予的权重越大［8-9］.图4为采用反距离加权（IDW）插值后地统计分析获得的A网与B网的年均pH值空间分布.从图4可知，A网与B网的酸雨区空间分布存在很大不同.对A网、B网和AB网合成的三种酸雨监测数据进行插值与地统计分析，计算酸雨空间分布面积，结果见表3.从表3可见，由于两个监测网在监测点数量、空间分布的不同，在同一插值与地统计方法下所获得的酸雨区的分布与面积存在巨大的差异.

从同一监测网随机抽取不同监测站点样本以及不同监测网酸雨监测数据的插值与地统计分析结果表明，酸雨监测网站点数的多少及其空间分布对确定酸雨区的分布及面积有很大的影响.

图3 2008年不同部门酸雨监测网站点分布Fig.3 Distribution of acid rain monitoring sites of different department in 2008

图4 2008年A酸雨监测网与B酸雨监测网年均pH值空间分布Fig.4 Spatial distribution of annual pH value of Acid Rain Monitoring Network A and B

当酸雨监测网的站点数量足够多时，酸雨监测站点的空间布置显得尤为重要.普通克里格插值方法不仅可以预测空间分布，而且可以对预测的不确定性进行空间分析［10-11］.图5为普通克里格插值预测酸雨发生概率分布与预测标准误差分布.

从图5可知，我国酸雨主要发生在东南部地区，即酸雨发生概率较大的地区，而酸雨监测站点稀少的地方预测标准误差也大.概率≥0.5的面积比为16.38%，概率≥0.2的面积比为25.86%.预测标准误差≤0.8的面积比为42.87%，＞1的面积比为4.84%.若用AB网合成数据可以进一步降低预测标准误差，AB网合成预测标准误差＞1的面积比下降到3.11%，＞0.9的面积比从原先的25.15%下降到22.08%.由图5可知，B网的监测站点与A网的监测站点具有较好的互补效果.今后酸雨监测网站点的建设应优先考虑在预测标准误差大的地方进行布点，以减少空间分析的不确定性，降低预测误差，提高预测精度.

表3 不同酸雨监测网酸雨区面积比（%）Table 3 Area ratio of acid rain area of different Acid Rain Monitoring Network（%）

图5 普通Kriging预测酸雨发生概率分布与预测标准误差分布Fig.5 Prediction probability and prediction standard error of Ordinary Kriging interpolation

2 空间插值方法与参数设置

2.1 空间插值方法

由于环境条件、财力、物力和人力等多种原因的限制，酸雨监测站点的空间分布及数量难于达到一个监测站点所能表征的足够小的空间分辨率，在实际布点上也没有这个必要.酸雨区的空间分布是客观存在的，除了合理布点较好地反映酸雨区的空间分布外，不同的空间插值方法对酸雨区的空间分布的表征与描述也存在差距［12-14］.

本文采用IDW和Kriging两种插值方法进行比较分析.IDW插值综合了泰森多边形的自然邻近法和多元回归渐变方法的长处，在插值时待估点Z值为邻近区域内所有数据点的距离加权平均值.权重函数与待估点到样点间的距离的U次幂成反比，即随着距离增大，权重呈幂函数递减.且对某待估点而言，其所有邻域的样点数的权重和为1，IDW是一种全局插值法和精确插值法.地统计插值引入了概率模型，即地统计插值认为从一个统计模型不可能完全精确地得出预测值，所以在进行预测时，应该给出预测值的误差，即预测值在一定概率内合理［9］.通常所说的地统计插值是指克里格插值法（Kriging），它是以区域化变量理论为基础，以变差函数为主要工具，在保证估计值满足无偏性条件和最小方差条件的前提下求得估计值［10］.无偏是指偏差的数学期望为0，最优是指估计值与实际值之差的平方和最小.

图6为A网分别采用地统计分析的IDW插值法与Kriging插值法获得的年均pH值的空间分布，即酸雨区空间分布.IDW插值采用幂指数优化，幂指数Power为1.57，普通克里格插值采用球形模型，其余采用系统缺省值.从图6可见，IDW插值法的重酸雨分布比Kriging插值法多而广，但酸雨区的分布Kriging插值法比IDW插值法略广而连续.表4为两种插值方法的酸雨区面积统计结果.

在表3中，首先，利用空间分析工具中的IDW插值方法（幂指数为缺省值2），将散点数据通过插值产生栅格数据，栅格大小为0.1度，而在地统计分析中无法对栅格大小进行控制，但可以对幂指数进行优化；其次，利用地统计分析工具，直接对前面产生的栅格数据进行插值，插值方法仍旧采用IDW插值法，并对幂指数进行优化，最终获得A网酸雨区面积.而表4中，地统计IDW插值方法没有进行栅格化，直接用地统计分析的IDW插值法，并对幂指数进行优化处理，最终获得A网酸雨区面积.对比表3的A网与表4的地统计IDW，可以发现首先对数据进行栅格化获得的重酸雨区面积要大于直接用地统计分析方法，这种情况在A网200个随机样本中表现尤为明显，采用地统计分析方法时，A网200个随机样本没有重酸雨区分布，酸雨区占全国的比例为18.59%，而采用先插值栅格化后地统计分析中，A网重酸雨区占全国比例为0.32%，酸雨区占全国比例为18.26%（表2）.由此可见，不同的插值过程也会对插值结果产生影响，地统计分析由于无法对栅格大小进行控制，会导致重酸雨监测站点分布频率小而分散时被忽略的现象（20个监测站点pH≤4.5，占总样本数的10%，分布在广西、湖南、湖北、浙江、江西、江苏、上海、云南等地）.

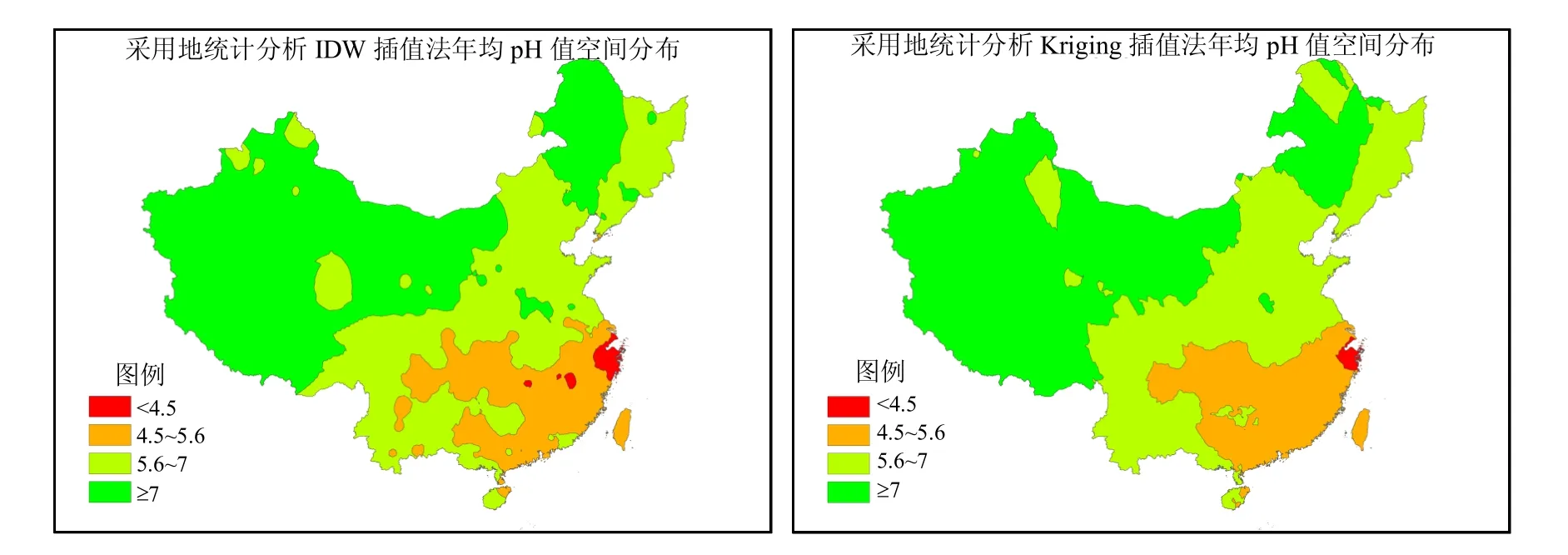
图6 不同地统计分析插值方法下的酸雨空间分布Fig.6 Spatial distribution of acid rain under different geostatistics analysis interpolation method

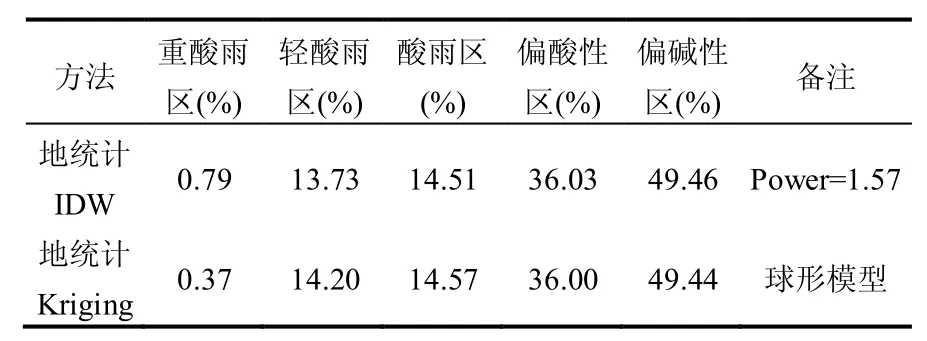
表4 不同地统计分析插值方法下酸雨区面积统计结果Table 4 Statistical result of acid rain area under different geostatistics analysis interpolation method

2.2 不同参数设置

采用地统计分析的IDW插值方法对A网酸雨监测数据进行酸雨空间分布分析，分别设置幂指数值为1、2和3，并利用幂指数优化功能获得优化后的幂指数值为1.57，其余参数均采用缺省值，这样形成了地统计分析的IDW插值方法的4种不同参数设置的空间分析方案，其地统计分析获得的酸雨区面积见表5.

表5 地统计分析IDW插值法4种不同幂指数值的酸雨区面积（%）Table 5 Acid rain area of four different exponential values of IDW interpolation method（%）

从表5可见，重酸雨区面积比差距较大，幂指数值为3的插值方案重酸雨区面积比最大，比最小的幂指数值为1的大1倍多，面积比差值达0.68%；轻酸雨区面积比变化在13.57%～13.87%之间，酸雨区面积比变化在14.51%～14.93%之间.

同时，采用地统计分析的普通克里格插值方法通过选择不同的变异函数模型对A网酸雨监测数据进行酸雨空间分布分析，其余参数均采用缺省值.ArcGIS提供的变异函数模型有Circular（圆形）、Spherical（球形）、Tetraspherical （四球形）、Pentaspherical （五球形）、Exponential （幂）、Gaussian （高斯）、Rational Quadratic（有理二次函数）、Hole Effect（空穴效应）、K-Bessel（K-贝塞尔）、J-Bessel（J-贝塞尔）和Stable（稳定的）等11种模型［15-17］.另外，在球形模型下，选择“显示搜索方向”，设置方向角度为32度.这样形成了地统计分析的普通克里格插值方法12种不同参数的空间分析方案，计算结果见表6.

表6 地统计分析Kriging插值法12种不同幂指数值的酸雨区面积（%）Table 6 Acid rain area of twelve different exponential values of Kriging interpolation method（%）

从表6可见，重酸雨区面积比差距较大，幂指数模型方案重酸雨区面积比最大，比最小的空穴效应模型大1倍多，面积比差值为0.22%；轻酸雨区面积比变化在13.92%～14.63%之间，酸雨区面积比变化在14.35%～14.84%之间.

从地统计分析的IDW与Kriging插值方法不同参数的空间分析结果来看，同一种插值方法下，重酸雨区、轻酸雨区和酸雨区的空间分布及面积没有很大的差异，相比较而言IDW的变化略比Kriging大些.

3 面积比计算方法

面积比计算方法分为网格法与等值面法两种，网格法利用等间距网格插值获得的栅格数据或者利用地统计分析结果导出的网格数据，通过统计每种类型的网格数除于总网格数得到面积比［18-20］.等值面法利用地统计分析结果导出等值面（填充的等值线）数据，再通过投影转换和地图裁切的手段获得整个区域的空间分布的等值面，然后进行各类区域的面积计算除于总面积得到面积比.后者等值面法是精确计算面积比的方法，而前者网格法存在一定误差，造成误差的主要原因是计算区域边界一般是不规则的曲线，边界网格只包含实际区域的一部分，当一个网格代表的面积较大时，误差也随之变大.如果采用的网格是经纬度网而不是公里网的话，由于每个网格所代表的面积不同，网格面积从低纬度向高纬度逐渐减少，在这种情况下，利用网格法计算面积比误差将更大.

表7 不同面积比计算方法与站点类型的空间分析结果Table 7 Statistical result of spatial analysis of different area ratio computational method and monitoring site types

表7为不同面积比计算方法获得的酸雨区比例.从表7可见，在采用城市站点数据时，网格法计算的重酸雨区、酸雨区面积比均小于等值面法，尤其重酸雨区面积网格法只有等值面法的1/2.空间分析样本采用酸雨监测站点数据与综合平均后的城市站点数据，在统一的等值面法下，2006年和2008年重酸雨区城市站点大于监测站点，2006年酸雨区城市站点小于监测站点.将监测站点数据综合平均成城市站点数据容易造成低pH值凸显与高pH值的消失，以及空间位置的不确定性.

4 结语

影响精确界定我国酸雨区空间分布的首要因素是酸雨监测网的站点数量及其空间分布，其次是选择正确、合适的空间插值方法及其相应参数的设置，最后是精确的面积测算方法.我国酸雨监测网建设应优先在西藏、内蒙古北部及西部等地区布点，目前可以整合两个部门的酸雨监测网，统一监测方法，共享监测数据.空间分析插值方法的评价表明，采用先IDW插值形成栅格数据再使用地统计分析的IDW进行预测、插值的空间分析技术路线，交叉验证三项指标均显著好于直接使用地统计分析，进行酸雨区空间分析时应采用多种插值方法进行比较与分析评估，确保在现有酸雨监测网的基础上获得最精确、可靠的酸雨区空间分布.

［1］王文兴.中国酸雨成因研究 ［J］. 中国环境科学， 1994，14（5）：323-329.

［2］刘炳江，郝吉明，贺克斌，等.中国酸雨和二氧化硫污染控制区划及实施政策研究 ［J］. 中国环境科学， 1998，18（1）：1-7.

［3］WANG W X， WANG T. Short communication on acid rain formation in China ［J］. Atmos Environ， 1996，30（23）：4091-4093.

［4］云雅茹，柴发合，王淑兰，等.欧洲酸雨控制历程及效果综合评述［J］. 环境科学研究， 2010，23（11）：1361-1367.

［5］环境保护部.2013中国环境状况公报［EB/OL］. 2014［2014-06-05］. http：//jcs.mep.gov.cn/hjzl/zkgb/.

［6］朱求安，江 洪，宋晓东.基于空间插值方法的中国南方酸雨时空分布格局模拟及分析 ［J］. 环境科学研究， 2009，22（11）：1237-1244.

［7］丁国安，徐晓斌，王淑凤，等.中国气象局酸雨网基本资料数据集及初步分析 ［J］. 应用气象学报， 2004，15（S1）：85-94.

［8］封志明，杨艳昭，丁晓强，等.气象要素空间插值方法优化 ［J］. 地理研究， 2004，23（3）：357-364.

［9］陈欢欢，李 星，丁文秀. Surfer 8.0等值线绘制中的十二种插值方法 ［J］. 工程地球物理学报， 2007，4（1）：52-57.

［10］庄立伟，王石立.东北地区逐日气象要素的空间插值方法应用研究 ［J］. 应用气象学报， 2003，14（5）：605-615.

［11］李 新，程国栋，卢 玲.青藏高原气温分布的空间插值方法比较 ［J］. 高原气象， 2003，22（6）：565-573.

［12］刘登伟，封志明，杨艳昭.海河流域降水空间插值方法的选取 ［J］.地球信息科学， 2005，8（4）：75-79.

［13］HUTCHINSON M F， GESSLER P E. Splines-more than just a smooth interpolator ［J］. Geoderma， 1994，62：45-67.

［14］林忠辉，莫兴国，李宏轩.中国陆地区域气象要素的空间插值 ［J］.地理学报， 2002，57（1）：47-56.

［15］邬 伦，刘 瑜，张 晶，等.地理信息系统-原理、方法和应用［M］. 北京：科学出版社， 2001：89-190.

［16］徐贞元，江 欣.浅谈环境信息中的GIS技术和中介数据 ［J］.环境科学研究， 1997，10（5）：9-13.

［17］张攀攀，王义祥，邬群勇，等.GIS与大气环境模型的集成及其应用 ［J］. 环境科学研究， 2010，23（5）：575-580.

［18］孙英君，王劲峰，柏延臣，等.地统计学的GIS空间分析功能扩展［J］. 华侨大学学报（自然科学版）， 2004，25（4）：435-439.

［19］杜迎燕.基于网格的面雨量实时计算方法研究 ［D］. 南京：河海大学， 2006：7-15.

［20］孟俊贞.克里金插值近似网格算法在栅格数据投影变换中的应用 ［D］. 长沙：中南大学， 2009：11-22.

Study on the influence factors of accurate definition of the spatial distribution of acid rain area in China.

HU Bing-qing1*， YI Peng1， DUAN Ning1， ZHAO De-gang1， ZHAO Jin-min1， CHENG Ke2（1.Chinese Research Academy of Environmental Sciences， Beijing 100012， China；2.Key Laboratory for Yellow River and Huaihe River Water Environmental and Pollution Control， Ministry of Education， School of Environment， Henan Normal University， Xinxiang 453007， China）. China Environmental Science， 2015，35（3）：917～924

The influential factors of accurate definition of the spatial distribution of acid rain area was analyzed based on the monitoring data of Acid Rain Monitoring Network in China. The results showed that the number and spatial distribution of the sites of Acid Rain Monitoring Network were the primary influence factor， which can cause a great difference to the acid rain distribution by using the same interpolation and geostatistical analysis methodologies. The secondary factor was the selection of a proper spatial interpolation method and corresponding parameter settings. As the result， the distribution size of heavy acid rain area that obtained by using the IDW interpolation was larger and wider than that used the Kriging method. Moreover， a precise calculation method for area ratio was another key factor. The ratio of heavy acid rain area got based on the grid method was smaller than that obtained from the isosurface method. The research suggests that some areas should be given a priority consideration for the establishing of Acid Rain Monitoring Network such as Xizang， north and west of Inner Mongolia. In addition， multiple interpolation method should be applied for the spatial analysis of acid rain area so as to obtain the precise and reliable distribution data.

acid rain area；spatial analysis；geostatistical analysis；interpolation effects evaluation

X517

A

1000-6923（2015）03-0917-08

胡炳清（1963-），男，浙江慈溪人，研究员，学士，主要从事环境管理技术、环境系统模拟、环境管理系统与平台研发、环境规划与评价.发表论文28篇，出版专著1部，合作出版专著4部.

2014-07-31

国家“973”计划（2005CB422200）；环保公益性行业科研专项（201209003，201209001）

* 责任作者， 研究员， hubq@craes.org.cn