街道峡谷对称性对污染物扩散的影响

杨 方，钟 珂，亢燕铭（东华大学环境科学与工程学院，上海 201620）

街道峡谷对称性对污染物扩散的影响

杨 方，钟 珂，亢燕铭*（东华大学环境科学与工程学院，上海 201620）

采用数值模拟的方法，研究了行列式和错列式街谷两侧建筑物的对称性对街谷内和下游建筑尾流区污染物浓度的影响，并引入3个用于评价室内空气环境的指标来描述街谷中人员区域内的空气质量.结果表明，平均残留时间（ART）和有效通风率（PFR）可用于评价不对称街谷内的空气质量.街谷的不对称性对街谷内部和下游建筑尾流区污染物浓度分布均有明显影响.下游建筑越低，则尾流区的浓度越高.行列式和错列式街谷中人员活动空间的无量纲平均浓度分别在建筑高度比例为7/3和7/2时最大.为在城市规划中尽可能避免出现最不利比例的街谷，根据平均残留时间和有效通风率等指标，给出了上下游建筑高度比与最不利街谷改善率的关系.

非对称街道峡谷；街谷上下游建筑高度比；最不利比例街谷；有效通风率；平均残留时间

随着我国机动车保有量的逐年增加，道路交通排放已成为导致城市空气环境质量持续恶化的主因之一.城市街道峡谷（简称“街谷”）中的流场性质和机动车尾气扩散特征与街谷结构密切相关.街道两侧的临街建筑高度相等时，构成对称型街谷；道路两侧建筑高度相差较大时，则构成非对称街谷.随着城市规划的多样性发展，不对称街谷越来越普遍.

大量文献针对街谷流场和污染物分布特征进行了研究［1-9］，但大多数都是关于街道两侧建筑物高度相等的情况［1-6］，而关于非对称街谷内部流场和污染物浓度分布特征的研究较少.Xie等［8］研究了街道两侧建筑物高度的比值对街谷内涡流结构的影响.何泽能等［9］通过模拟不同高度比的街谷内流场，指出峡谷的对称性对其内部气流场有显著影响.Hang等［10］的研究表明，在非对称建筑群中，相对于湍流作用，水平和垂直方向的平均流对污染物扩散的影响较大.汪立敏等［11］指出，当下游建筑高度低于上游建筑时，街谷内的流场及浓度场与对称街谷时相似.当下游建筑高于上游建筑时，街谷内的流场较之对称街道峡谷有较大的变化.罗昔联等［12］的研究表明，上游建筑高于下游建筑的非对称街谷中，街谷内颗粒物浓度远高于同类型其它几何尺寸街谷.

尽管上述研究考虑了非对称街谷中的气流运动和污染物空间分布特征，但关于不对称性对街谷内人员活动区空气品质的影响效果尚未涉及，缺乏可供城市规划设计师参考的合理建议.为深入了解街谷不对称性形成的气流特征对机动车尾气扩散的影响，以寻求街谷不对称程度与街谷内空气品质的量化关系，本文利用计算流体力学方法，研究分析三维街谷中上、下游建筑高度比对街谷内以及下游建筑尾流区气流和污染物浓度分布的影响.同时，为了更好地评价气流对街谷中污染物的清除效果，引入相关的通风效率指标对街谷内空气质量进行评价，为城市的合理规划提供理论依据和参考数据.

1 物理模型与计算方法

为获得街谷不对称性对气流和污染物扩散影响的详细信息，对街道边界做了简化，分别对街道两侧建筑为规则排列的行列式布局和错列式布局的街道模型结构进行数值模拟.图1给出了行列式和错列式建筑布局构成的街谷，以及计算域尺寸.图中还给出了随后分析中涉及到的部分几何参数（图中A-A为垂直方向剖面，位于建筑物1/4长度处；L1、L2为街谷呼吸高度处沿街道分布的直线，分别靠近街谷端部和中心）.

图1 不同建筑布局构成的街谷模型和计算域的尺寸Fig.1 Sketch of street canyon models for different building arrangements and the computational domain

设所有临街建筑长60m （L），宽15m （B），街宽为30m （W），街道同侧相邻建筑间距S=20m，因而临街建筑物在y方向成周期性排列.考虑街谷内污染物扩散最不利的情况，设来流风向垂直于街谷轴线.此时，所形成的街谷流场也呈周期性空间分布.因此，为节约计算成本，采用镜像法，通过设置对称面，仅计算图1（a）和（b）中虚线区域.本文针对临街为多层建筑的街谷进行研究，建筑物最大高度为21m.数值模拟中，为尽量消除计算区域有限导致的端部效应，模拟时做如下处理［13-14］，迎风的首排建筑距求解区域上游边界为12H，末排建筑距区域下游出口17H，建筑顶部距上方自由边界面5H.如图1（c）所示.使用非结构网格划分计算空间，为保证给出更细致的近壁面处的计算结果.经过网格独立性测试后，建筑物附近最细网格为0.3m，模拟区域的网格总数为310～370万.

设街谷两侧上游和下游建筑物高度分别为H1和H2，分别针对不同的H1和H2组合进行模拟计算，具体组合情况见表1.

设模拟区域的入口处流速均匀，并将其边界设为速度进口；由于出口处可视为充分发展湍流，故将出口边界条件设为outflow.地面和建筑表面为无滑移壁面，计算域壁面则设为有滑移壁面.

湍流特性和风速的垂直特性受地形的影响，并与地形的粗糙度有着密切的关系.计算域入口风速的垂直特性由幂指数律给出，如下式所示：

表1 上、下游建筑的高度Table 1 Heights of upwind and downwind buildings

式中：z为任一高度，m；Vz为任一高度处的平均风速，m/s；α为地面粗糙度指数，地形越粗糙，地表对气流的阻滞作用越强，α也越大，根据相关文献［16］，这里α=0.25；h为标准参考高度，m；Vh为在此高度处测得的标准参考风速，m/s，在本文中定义最高建筑屋顶高度处（H=21m）的风速为屋顶风速Vr.我国长江中下游地区平均风速通常在1.4～5.3m/s［17］，对应的流动Reynolds为2×106～7.6×106.此时流场处于自模区范围内［18］，即风速的变化不会对研究结论有较大的影响.本文对屋顶来流风速Vr=2.0m/s时进行模拟计算.

为模拟机动车尾气排放，将交通污染源视作连续均匀散发的线源，设置于街谷底部，它的中心轴线与街谷的中心线重合，宽10m，高0.5m.本文研究粒径为1μm的颗粒污染物的扩散和分布规律，污染源强度q0=0.02kg/s.为了便于比较，颗粒物浓度用无因次浓度C*的形式表示：

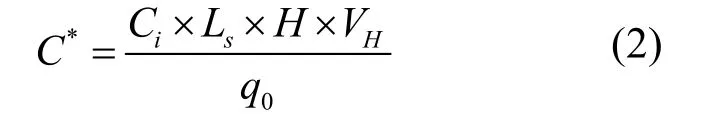
式中：Ci是i点处的颗粒物浓度，kg/m3；Ls为污染源长度，m.

2 模型的合理性验证

为了对所采用的数值模型进行可靠性验证，分别以Li等［19］和Meroney等［20］关于街谷流场和浓度分布的实验参数（包括街谷几何参数、流动参数和污染物参数）为基本数据，利用本文拟采用的离散模式、网格划分方法和计算控制等对二者的实验分别做了数值再现.其中速度场采用Li等［19］的水槽实验结果，并沿水平（x方向）和垂直（z方向）两个方向同时考察风速廓线；在速度场得到验证后，继续求解浓度场，对比数据采用Meroney等的实验结果.图2给出了数值计算结果与上述实验研究结果的比较.由于近年来，有研究建议用大涡模拟分析街谷流动问题，图中也以Liu等［21］的模拟为例，给出了大涡模拟速度场计算曲线.

图2 风速和浓度数值计算结果与实验数据的比较Fig.2 Comparisons of wind speed and concentration between numerical results and the experimental data Vzx和Vzz为分z方向的风速分量

由图2（a）和图2（b）可以看到，本文与Liu等［21］的大涡模拟结果在街谷内大部分区域均与实验结果吻合得较好，这说明本文的湍流模型能够正确计算街谷内流场情况.图2（c）中的背风区浓度计算结果与实测也符合得较好，迎风区则完全吻合.表明本文采用的计算方法可以很好地预测街谷内的气流流动和污染物浓度分布.

3 结果与讨论

3.1 街谷对称性对建筑周围流场和颗粒物平均浓度的影响

街谷两侧建筑物高度不同时，来流受到的阻挡作用不同，从而导致街谷内涡流结构与对称性密切相关.图3仅以行列式的A-A剖面［图1（a）］为例，给出了H1/H2不同时，建筑周围气流的流线和颗粒物浓度分布情况.

图3 行列式街谷中A-A剖面上（y=25m）流场和污染物无量纲浓度分布Fig.3 Flow field and dimensionless concentration distributions at A-A plane （y = 25m） for regular arrangement

从图3可以看出，当H1/H2不同时，不仅街谷内的气流分布和浓度分布不同，下游建筑尾流区域的流场和浓度场分布也不同.对于上阶梯型街谷［图3（a）］，来流在下游建筑的阻挡下，在街谷内存在两个顺时针旋转的涡流，在横向方向上几乎各占街谷的一半.在涡流的作用下，机动车排放的污染物被输送到背风面，再通过背风面屋顶处排出街谷，并很快被来流稀释，已流出污染物几乎没有再次流进街谷，街谷中机动车排放的污染物流入下游建筑尾流区的量很小.在完全对称的等高街谷中，街谷内仅有一个顺时针涡流［图3（b）］，在涡流的作用下，污染物在背风面和地面产生堆积，浓度随着高度的递增而减少.此时从背风面屋顶排出的污染物一部分再次流进街谷，一部分流入尾流区.对于下阶梯型街谷［图3（c）］，街谷中存在一个范围相对较大的涡流，涡流通过下游建筑屋顶延伸至尾流区，因而街谷中污染物容易被带出街谷，进入尾流区，使得尾流区浓度相对较高.

街谷内不同高度处的污染物浓度有很大区别，因此以不同的高度（或高度范围）的污染物浓度数据进行分析讨论产生的结论可能是不同的，降低街谷内行人的呼吸浓度是改善街谷空气品质的根本目的，因此本文针对人员活动空间内（高度在2m以下）的平均浓度进行分析讨论.并统一采用人员活动空间内（高度在2m以下）的平均浓度来评价街谷空气品质.

本文关注尾流区内距离下游建筑背风面30m以内区域的污染物浓度.图4给出了街谷中和下游建筑尾流区的人员活动空间内污染物浓度的无量纲值与建筑高度比（即不对称性）的关系，同时也给出了尾流区和街谷中人员活动空间污染物浓度之比k，即：

从图4（a）可以看出，行列式街谷人员活动空间内平均浓度受对称性影响很大，在H1/H2=7/3时，街谷人员活动空间内平均浓度最大.而尾流区人员活动空间中的平均浓度几乎不随对称性变化而改变，在H1/H2=3/7～7/2，几乎为常数，并且相对街谷人员活动空间内浓度都很小.这使得尾流区和街谷中人员活动空间污染物浓度的比值k几乎完全受控于街谷浓度.还可以看到，当街谷为上阶梯极不对称（H1/H2=1/7）时，下游建筑有效地保护了尾流区；当街谷为下阶梯极不对称（H1/H2=7/1）时，上游建筑对污染物扩散的阻挡作用迫使机动车尾气在近地面区域扩散开，由于下游建筑过低，造成尾流区的人员活动空间浓度相对于街谷内人员活动空间浓度不可忽略.

图4 下游建筑尾流区与街谷人员活动空间的无量纲浓度及其浓度比Fig.4 Dimensionless pollutant concentrations in the downstream building wake regions and street canyons and the ratios between the two

由图4（b）可以看到，对于H1/H2＜1的上阶梯式街谷，错列式街谷尾流区的人员活动空间几乎不受污染；而在下阶梯式街谷中，尾流区浓度随着下游建筑高度的降低而增大，同样是因为下游建筑越低，对尾流区的保护作用越弱.街谷人员活动空间内平均浓度最大值出现在H1/H2=7/2.尾流区和街谷中人员活动空间污染物浓度之比k随着H1/H2单调增大.

3.2 街谷不对称性对街谷内浓度分布规律的影响离地1.5m高度处是行人平均呼吸高度.为了比较街谷不对称性对街谷内颗粒物浓度水平分布的影响，图5和图6分别给出了1.5m高度处行列式和错列式街谷在靠近上游建筑端部和中心［具体位置见图1（a）和图1（b）中的直线L1和L2］处颗粒物浓度的水平变化曲线.

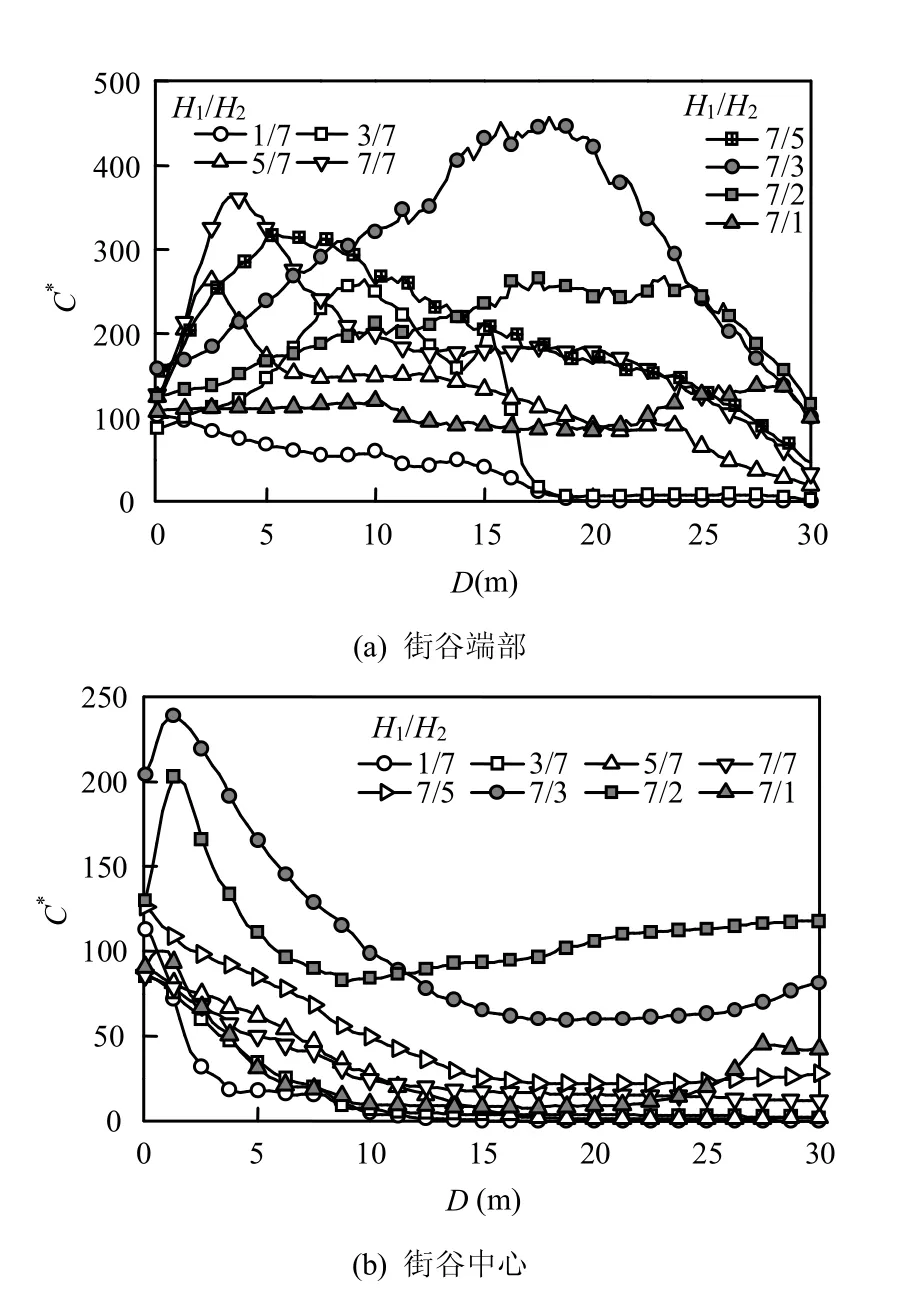
图5 行列式街谷内行人呼吸高度处（z = 1.5m）颗粒物浓度分布Fig.5 Dimensionless pollutant concentration distributions along the streets at the breathing levels （z = 1.5m） inregular canyons

由图5（a）可以看出，在靠近行列式街谷缺口处，H1/H2=7/3是临界点，这时最大浓度值发生在街谷中央附近.当H1/H2≤7/5时，浓度峰值发生在背风面附近.这是由于下游建筑高，对来流产生的较强阻挡作用所诱发的涡流将机动车排放的污染物输送至背风面，如图3（a）和（b）所示.此外还可以看到，H1/H2越接近1，即对称性越强，街谷内浓度最大值越高.当H1/H2＞7/3时，尽管浓度沿街道宽度方向变化较小，但明显可以看到迎风面附近浓度最大.同时街谷越对称，即H1/H2越接近1，浓度越大.

从图5（b）可以看出，不论对称性如何，街谷中心区的浓度分布特征均为背风区浓度高于迎风区浓度.同样，H1/H2=7/3是临界点，此时街谷中的浓度最大值最高，随着H1/H2偏离7/3，最大浓度逐渐变小.

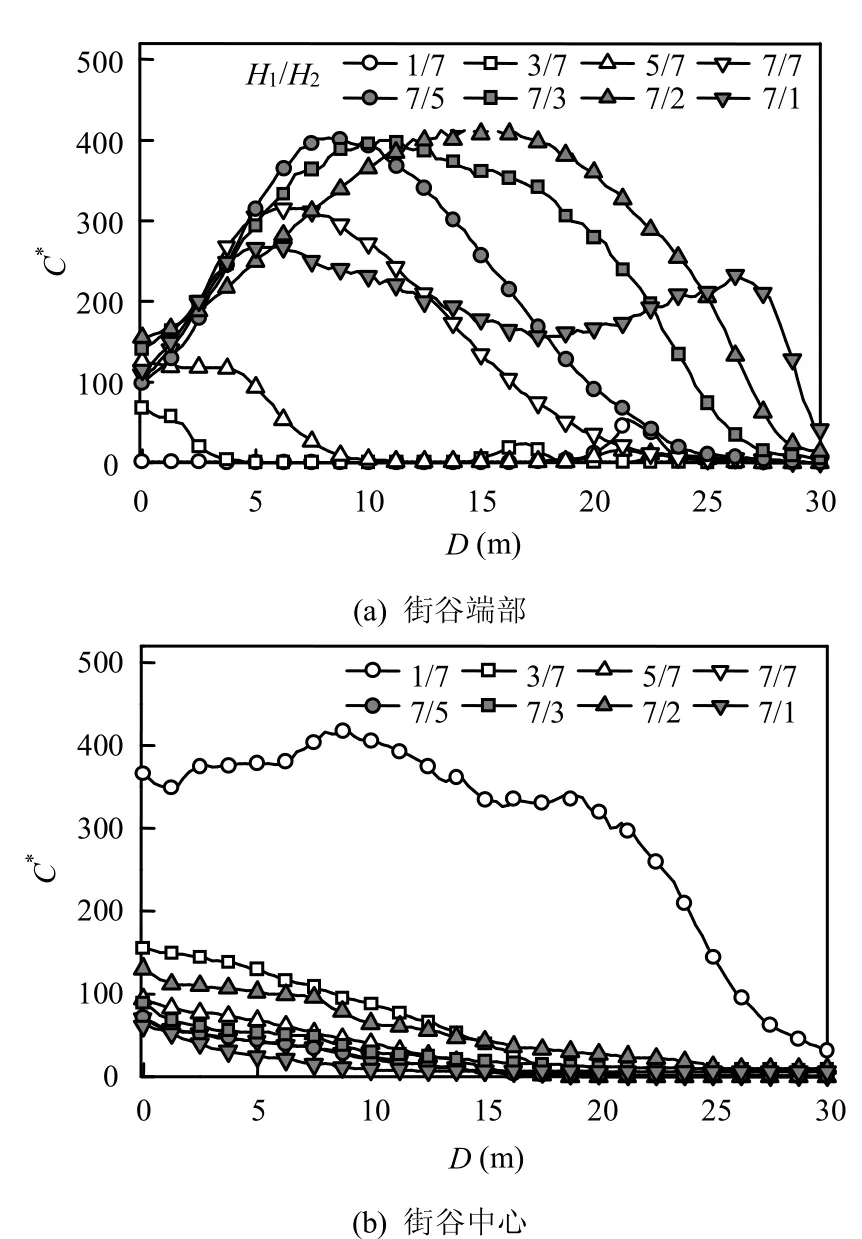
图6 错列式街谷内行人呼吸高度处（z = 1.5m）颗粒物浓度分布Fig.6 Dimensionless pollutant concentration distributions along the streets at the breathing levels （z = 1.5m） instaggered canyons

由图6（a）和6（b）可以看到，错列式街谷中，除了极不对称的下阶梯街谷中靠近上游建筑端部位置外，街谷不对称性不会改变背风区浓度偏高的特性，但浓度最大值会受到对称性的影响.与图5比较，可以认为，街谷不对称性对街道内污染物浓度分布规律的影响，在行列式街谷中的作用明显大于错列式街谷.

为了综合比较建筑布局对街谷行人呼吸域内污染物扩散的影响，引入3种原本用于评价室内空气质量的指标来描述街谷呼吸域内的空气质量.

有效通风率（PFR）：可以理解为将污染物赶出空间所需要的空气量，它反应了空气清除污染物的能力，其表达式为［22］：

式中：qp为污染物的产生速率，kg/s；ρ为空气密度，kg/m3；Cp为空间内污染物平均浓度，kg/kg.

访问频率（VF） 街谷内部分污染物在涡流作用下，可能出现被气流带出街谷后有再次进入街区的情况，访问频率VF用于表示一个污染气体微团进入空间的次数.空间中所有污染空气微团的平均访问次数可用公式（5）计算，VF值越小，表示较少的污染气体返回空间，气流清除污染物的能力较高.

式中：Δqp是颗粒物进入空间的流量，kg/s；Si为空间边界平面i的面积，m2；u是空气进入空间通过边界平面i时的平均速度，m/s；c是边界平面i的污染物浓度，kg/kg；n为空气进入空间通过的边界平面总数，u′是速度的波动量，m/s；c′是浓度的波动量，kg/kg.uc与ρSi相乘代表空间进气量，kg/s与ρSi相乘代表湍流扩散部分的进气量，kg/s.

平均残留时间（ART） 对于一个颗粒物或污染气体微团来说，残留时间被定义为污染物从最开始进入空间到最后离开空间的时间.可用下式计算：

应用平均值的概念，将VF和ART相乘表明空间内所有颗粒物的平均残留时间.V为空间体积，m3.

根据以上公式分别计算H1/H2不同时街谷各项指标的变化，图7分别给出了街谷内平均浓度和以上3种指标随着H1/H2的变化曲线.

图7 H1/H2对街谷人员活动空间内各项指标的影响Fig.7 Effect of ratios H1/H2on indices in the pedestrian domains

由图7可以看到，除了访问频率（VF），行列式街谷中另外两个指标和平均浓度的最不利值都出现在7/3，错列式街谷中另外3个指标的最不利值都出现在7/2，表明平均残留时间（ART）、有效通风率（PFR）和街谷人员空间平均浓度（C）都可以用于评价街谷不对称性对浓度分布的影响.本文中污染物产生速率恒定，此时有效通风率（PFR）与浓度（C）成反比关系，使用浓度（C）评价街谷内空气品质更直接明了，但若颗粒物产生速率或空气密度随时间发生变化，则适合采用有效通风率（PFR）评价街谷内的空气品质.

图7表明，行列式街谷和错列式街谷中，人员空间浓度最大值分别在H1/H2=7/3和7/2时，均为下阶梯式街谷.因此在规划街道时.应结合当地主导风向.尽可能避免这种街谷出现.

3.3 街谷不对称性与最不利街谷空气品质改善率

在城市规划中，应尽可能偏离最不利街谷比例，为此定义相对于最不利街谷时，实际街谷空气品质的改善率ηi为：

式中：Ai为待规划街谷的第i个评价指标的预测值；Ai0为最不利比例街谷内第i个评价指标的预测值.在本文条件下，有效通风率PFR与平均浓度C的改善率完全一致.但为了在污染物强度随时间发生变化时也能够全面反应空气品质的改善情况，图8给出街谷人员活动空间中指标PFR和ART的改善率ηi与建筑高度比的关系.

图8 H1/H2对街谷人员活动空间内各项指标改善率的影响Fig.8 Effect of ratios H1/H2on percentage decrease of the indices in the pedestrian domains

从图8可以看到，结合城市主导风向形成上阶梯式街谷，对街道内空气品质改善作用大于下阶梯式街谷.上阶梯式街谷两侧建筑的最佳比例H1/H2为3/7，此时空气品质改善率高达70～92%.据此，城市规划设计人员可以根据实际环境尽可能地避免出现最不利街谷设计，并明确由此对街谷空气品质的改善程度.

4 结论

利用三维数值模拟分别研究了行列式和错列式建筑布局中上、下游建筑高度比例对街谷内和下游建筑尾流区污染物分布的影响，并引入3种原本用于评价室内空气质量的指标来描述街谷人员活动空间内的空气质量.

4.1 街谷不对称性对街谷内部和下游建筑尾流区污染物浓度分布均有明显影响.下游建筑越低矮，下游建筑尾流区浓度越高.

4.2 尽管平均残留时间ART和有效通风率PFR是为评价对称街谷空气品质而提出的，但本文计算结果表明，在评价不对称街谷空气品质时，平均残留时间ART和有效通风率PFR是适用的.

4.3 当街谷两侧为多层建筑时，行列式和错列式街谷中上下游建筑高度比例分别为7/3、7/2时为最不利于机动车尾气扩散的街谷尺寸，相对于最不利比例街谷，上阶梯式街谷的空气品质改善率高于下阶梯式街谷.为便于城市规划中尽可能避免出现最不利比例街谷，本文给出了上下游建筑高度比与最不利街谷空气品质间的关系.

［1］Huang Y， Zhou Z. A numerical study of airflow and pollutant dispersion inside an urban street canyon containing an elevated expressway ［J］. Environmental Modeling and Assessment，2013，18（1）：105-114.

［2］Wang Y， Zhong K， Zhang N， et al. Numerical analysis of solar radiation effects on the flow patterns in street canyons ［J］. Engineering Applications of Computational Fluid Mechanics，2014，8（2）：252－262.

［3］Ng W， Chau C. A modeling investigation of the impact of street and building configuration on personal air pollutant exposure in isolated deep urban canyons ［J］. Science of the Total Environment， 2014，468-469（15）：429-448.

［4］Vardoulakis S， Fisher B E A， Pericleous K， et al. Modelling air quality in street canyons： a review ［J］. Atmospheric Environment，2003，37（2）：155-182.

［5］胡 伟，钟 秦.壁面加热作用对街道峡谷污染物扩散的影响［J］. 中国环境科学， 2009，29（9）：908-913.

［6］王 乐，张云伟，顾兆林.动态风场及交通流量下街道峡谷内污染物扩散模拟 ［J］. 中国环境科学， 2012，32（12）：2161-2167.

［7］邵 毅，张述文，左洪超，等.榆中县城大气污染物扩散的观测实验与数值模拟 ［J］. 中国环境科学， 2013，33（7）：1223-1230.

［8］Xie X， Huang Z， Wang J. The impact of urban street layout on local atmospheric environment ［J］. Building and Environment，2006，41（10）：1352-1363.

［9］何泽能，高阳华，李永华，等.城市街谷峡谷对称性对内部气流场的影响研究 ［J］. 气象与环境学报， 2008，24（2）：62-67.

［10］Hang J， Li Y， Sandberg M， et al. The influence of building height variability on pollutant dispersion and pedestrian ventilation in idealized high-rise urban areas ［J］. Building and Environment，2012，56：346-360.

［11］汪立敏，王嘉松，黄 震，等.优选数值计算方法用于不对称街道峡谷的研究 ［J］. 水动力学研究与进展， 2005，20（1）：1-7.

［12］罗昔联，顾兆林.基于DPM模型的街谷内颗粒物扩散特性研究［J］. 中国科学院研究生院学报， 2007，24（5）：578-583.

［13］Liu C， Wong C C C. On the pollutant removal， dispersion， and entrainment over two-dimensional idealized street canyons ［J］. Atmospheric Research， 2014，135-136：128-142.

［14］Gromke C， Buccolieri R， Sabatino S D， et al. Dispersion study in a street canyon with tree planting by means of wind tunnel and numerical investigations-Evaluation of CFD data with experimental data ［J］. Atmospheric Environment， 2008，42（37）：8640-8650.

［15］Nazridoust K， Ahmadi G. Airflow and pollutant transport in street canyons ［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2006，94（6）：491-522.

［16］Barratt R. Atmospheric dispersion modelling - an introduction to practical applications ［M］. London： Earthscan Publication， 2001.

［17］GB50736-2012 民用建筑供暖通风与空气调节设计规范 ［S］.

［18］Bird R B， Steuart W E. Transport Phenomena ［M］. 2ndEd. New York： John Wiley and Sons， Inc， 2002.

［19］Li X， Leung D Y C， Liu C H， et al. Physical modeling of flow field inside urban street canyons ［J］. Journal of Applied Meteorology and Climatology， 2008，47：2058-2067.

［20］Meroney R N， Pavageau M， Rafadalis S， et al. Study of line source characteristics for 2-D physical modelling of pollutant dispersion in street canyon ［J］. Journal of Wind Engineering and Industrial Aerodynamics， 1996，62（1）：37-56.

［21］Liu C， Barth M C， Leung D Y C. Large-eddy simulation of flow and pollutant transport in street canyons of different buildingheight-to-street-width ratios ［J］. Journal of Applied Meteorology，2004，43（10）：1410-1424.

［22］Kato S， Ito K， Murakami S. Analysis of visitation frequency through particle tracking method based on LES and model experiment ［J］. Indoor Air， 2003，13（2）：182-193.

Effects of street geometric configurations on the pollutant dispersion around the canyons.

YANG Fang， ZHONG Ke，KANG Yan-ming*（School of Environmental Science and Engineering， Donghua University， Shanghai 201620， China）. China Environmental Science， 2015，35（3）：706～713

The effect of street geometric configurations， i.e.， building height layout， on pollutant distributions in both regular and staggered street canyons and the wake region of the downstream buildings are estimated by using the computational fluid dynamic （CFD） simulations. Three ventilation efficiency indices for evaluating indoor environment are applied to assess the air quality in the pedestrian domain. The numerical results show that average residence time（ART） and purging flow rate （PFR） can be used to evaluate the air quality inside the street canyons. The flow field and pollutant distribution inside and outside the canyon are greatly influenced by the building height layout， and the pollutant concentration in the wake region increases with decreasing the downstream building height. The highest values of the average concentration may occur in the pedestrian domain when the height ratios of the upstream building to the downstream building， i.e.， H1/H2， are 7/3 and 7/2 for regular and staggered canyons， respectively. In order to avoid these unfavorable building height layouts during urban planning， the relationships between H1/H2and the percentage reductions in PFR and ART are analyzed for both the regular and staggered arrangements.

asymmetrical street canyon；height ratio of upstream building to downstream building；worst building height layout；purging flow rate；average residence time

X51， P463， TU119， TU984

A

1000-6923（2015）03-0706-08

杨 方（1988-），女，江苏连云港人，博士研究生，主要从事城市大气环境与室内空气品质研究.发表论文4篇.

2014-07-20

国家自然科学基金（40975093，41275157）；上海市教委科研创新重点项目（14ZZ073）

* 责任作者， 教授， ymkang@dhu.edu.cn