重庆库区钻孔应变与水位相关性分析

李光科 陈 凯 巩浩波

（中国重庆401147重庆市地震局）

重庆库区钻孔应变与水位相关性分析

李光科 陈 凯 巩浩波

（中国重庆401147重庆市地震局）

重庆库区多套钻孔应变仪受到水位或气压干扰，通过分析各地震台应变与水位、气压的关系，得出其相关系数、回归系数，并通过求得的关系式，去除水位、气压对应变观测值的影响。

钻孔应变；相关系数；回归系数；水位；气压

0 引言

2007年以来，重庆市地震局在重庆库区架设多套高精度RZB-2型电容式钻孔应变仪，该仪器采用先进电容式微位移传感器与高精度比率电桥测量技术，具有观测精度高、长期稳定性好、能进行现场标定等优点，并配有辅助水位、气压、井温探头，实现多分量观测，能够记录丰富的地壳动态应力场活动信息，且能清晰记录固体潮。

因为该仪器精度高，应变观测值易受降雨、气压、地下水位、供电等干扰影响，其中井内水位对测值影响较大，而上述干扰对应变值的影响可能掩盖前兆异常信息，给异常资料的提取带来困难。笔者根据重庆库区钻孔应变观测积累的大量连续可靠数据，研究应变与水位的相关性，尝试求出其相关系数和回归系数，从而提供解决重庆库区钻孔应变水位干扰的思路和方法。

1 观测资料质量评价

在研究应变与水位相关性之前，应对各仪器观测资料质量做出评价，选取钻孔元件与围岩耦合状态好、数据质量高的仪器进行分析计算，从而得到可靠结果，本文采用实地相对标定（邱泽华，2009）方法进行资料质量评价。

由于RZB-2型钻孔应变仪为四分量，实际解算平面应变参数只需要相互独立的3路观测值即可，四分量观测提供1路多余的观测结果，其优势在于仪器可以自检，从而提高观测结果的可靠性，所谓自检条件是指，当探头与围岩的耦合处于理想状况时，仪器测量数据满足

式中，可以将任意一个方位的元件观测值记为s1，依次顺时针旋转45°，分别记为s2、s3和s4。式（1）表明，任意两个互相正交元件的测值之和相等。由于探头与围岩实际耦合的情况不同或其他原因，导致4组测值并不完全符合此关系，需要根据一定假设对元件测值进行校正，即实地相对标定。令

式中，ki（k = 1，2，3，4）为各分量的标定系数，Si（i = 1，2，3，4）依次为各元件标定后的结果。假设

利用式（2）对式（3）进行展开，得

计算时，用4路观测值依次表示si（i=1，2，3，4），通过式（4）反演得到标定系数ki（i=1，2，3，4），进而得到相对标定后的结果Si（i=1，2，3，4）。

选取重庆库区巴南、石柱、梁平、垫江、万州、合川、奉节7个钻孔台站2010年1月—2012年10月数据进行计算，反演得到各台4元件的标定系数，计算结果见表1、图1。

由表1、图1可见，巴南台、石柱台、梁平台和垫江台计算结果较理想，标定系数均值在1附近，且偏差不大，反映了探头与围岩耦合较好，仪器格值一致可靠。因主机参数设置、元件故障和台址等固有因素，万州、合川、奉节地震台计算结果较差。

图1 重庆市钻孔应变台站标定系数结果Fig.1 The calibration coefficient result of borehole strainmeters at stations in Chongqing

表1 重庆市钻孔应变台站标定系数计算结果Table1 Calculation results of calibration coefficients of borehole strainmeters at stations in Chongqing

2 钻孔应变和水位（气压）关系分析

RZB-2型钻孔应变仪设计原理是：应变值减小为压，应变值增大为张。辅助水位仪设计原理是：观测值减小，水位降低；观测值增大，水位升高。图2（a）为梁平台2013年整点值曲线，从图中可见，水位与应变呈明显负相关形态（应变值减少为压，应变值增大为张）。这是因为，当钻孔井内水位升高时，钻孔周围岩石中水位相应升高，钻孔应变仪各元件受到的压力随之增大，而当水位降低时，压力相应减小，出现水位升—应变值降、水位降—应变值升的规律。

为了研究水位对应变的影响，排除水位干扰，定量分析二者关系，利用最小二乘法求解相关函数。由水位记录原理可知

式中：P是压强，H是水位值，ρ是水的密度，S是单位面积，F是水产生的压力，σ是应力。根据式（8）可知，应力与水位是线性关系，假设应变与水位关系服从公式（唐小勇，2002）

式中，Ai为各元件观测的应变量值（i=1，2，3，4）；H为水位（单位m）；K表示水位每变化1 m，应变对应变化量，故回归系数K的量纲为m-1；Bi为各元件经水位改正后的值。由此可以根据最小二乘法，求解回归系数K及相关系数R。

在具体分析各台站数据时，发现由于井孔所处地质构造、水文地质条件、探头和井孔耦合程度等因素，各台水位和应变的关系并非呈标准的负相关形态，如：梁平台水位对应变影响具有时间滞后效应，垫江台在不同时段兼有水位与气压影响，奉节台具有水位对应变影响在时间尺度上的不一致现象，需要根据实际情况具体分析。

在长时间段内，应变测值影响因素较多，例如：区域应力场变化、仪器故障、人为干扰等，故选择短时间内水位剧烈变化的几天或者几小时数据进行分析。分析认为，短时间内，对观测值影响最大的因素是水位，从而求得相关系数和回归系数能真实反映两者关系的本构特性。对相对标定结果较好，且受水位影响较大的梁平台和垫江台进行分析。

2.1 梁平台

梁平台水位对应变影响具有时间滞后效应，图2（b）为2011年9月28日—10月10日分钟值曲线，可见水位和各路元件应变峰值不同步，水位对应变值的影响明显滞后。

图2 梁平台应变、水位预处理曲线（a）2013年整点曲线；（b）2011年9月28日—10月10日分钟值曲线Fig.2 The preprocessing hourly mean value curves of strain and water level at Liangping Seismic Station

针对该滞后现象，采用滑动求解水位与应变相关系数极值点的方法。选定9月28日00:00—10月8日23:59的数据，利用相同时间长度的应变数据，滑动求解相关系数，应变数据段起始时刻每次往后滑动1 min，共滑动两天（2 880 min），求得相关系数极小值点（接近-1），即该水位数据段对应变影响的起始时刻，即可求得水位影响的滞后时间。计算结果见图3，可以看出，滑动两天时间内，水位与各路元件应变值的负相关程度均呈现先增大后减小的U型趋势，利用极值点求得4路元件受水位影响的滞后时间，分别为：1 006 min、1 040 min、1 009 min、1 131 min。

利用上述方法，选取52段数据，计算水位对各元件影响的滞后时间，结果显示，各路元件的平均滞后时间较一致，均约1 200 min，计算结果见表2（只列出其中7段计算结果）。

图3 梁平台2011年9月28日—10月10月水位与应变滑动相关系数曲线Fig.3 The preprocessing minutely value curves of strain and water level at Liangping Seismic Station from Sep.28 to Oct.10，2011

表2 梁平台不同时间段各元件水位影响滞后时间Table2 Delay time influenced by water level of elements at Liangping station in different periods

将元件滞后时间近似平均为1 200 min（20 h），利用平均滞后时间，重新整合水位与应变数据，消除水位影响滞后效应，进行相关、回归分析，得出4元件回归系数，计算结果见表3（只列出其中8段计算结果），可以看出，在短时间跨度的数据段中，各元件与水位的相关系数R在-0.99附近，且同一元件回归系数K接近，如2010年4月21—25日、2012年7月10—14日等数据段。上述结果表明，水位与应变相关性较好，可以认为，求得的回归系数K真实反映该台水位与应变的本构特性，4路元件与水位的关系式见式（10）—（13）。随着数据段时间跨度的增长，各元件与水位的相关性呈减弱趋势，求得的回归系数与短时间跨度的数据段具有明显偏差，如2010年7—9月、2012年3—10月。这些结果与上文关于长时间跨度数据会引入区域应力场变化、仪器故障、供电等干扰因素的判断契合。

由应变与水位的关系式Ai= KiH + Bi得到梁平台四元件的应变与水位关系式

2.2 垫江台

分析发现，垫江台2008—2009年应变与水位相关性大，2010年相关性开始减弱，而逐渐与气压呈现负相关形态。调查发现，2010年初仪器厂家对该井孔进行灌浆作业，以消除水位对应变的过度影响，灌入的水泥固结后减小管壁与周围岩石的间隙，减少周围岩石孔隙水的渗入，从而减弱水位与应变的相关性。随后，固结的水泥对已与周围岩石耦合好的探头有下压作用，促使探头与围岩产生微小缝隙，增强气压对应变的影响，从而使气压与应变逐渐呈负相关形态。

表3 梁平台不同时间段各元件观测值应变量与水位相关系数R及回归系数KTable3 Correlation coefficient R and regression coefficient K between observed strain and water level of elements at Liangping station in different periods

表4 梁平复平台应变—水位回归系数KTable4 Regression coefficient K between strain and water level at Fuping station，Liangping

利用2号元件（N60E） 2009年1月—2011年6月的整点值数据，求解应变同水位、气压在一定时间长度上相关系数变化，可以较好反映上述现象。如图4，两条曲线纵坐标第1个值分别代表2009年1月1日0时—2009年1月31日23时水位、气压与应变的相关系数（数据段时间长度为31天，共744小时），以此类推，以后每个值均代表第1个数据段起始时刻往后推移一个整点，数据段长度为744小时的相关系数结果。从图4可见，应变与水位、气压相关系数曲线拐点几乎同时出现在2010年1月，之后应变与气压逐步呈负相关形态，水位与应变的负相关形态则逐渐消失，进一步印证厂家井孔灌浆作业减弱水位影响、放大气压影响的事实。

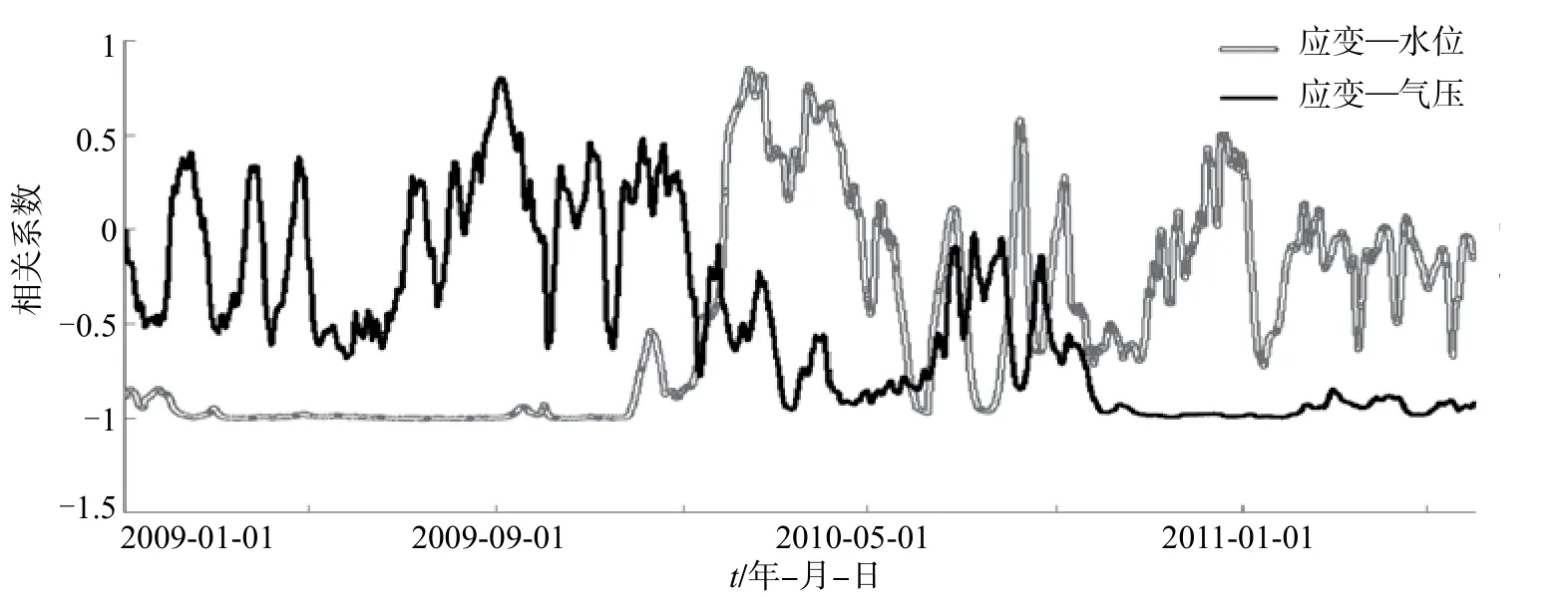
图4 梁平台N60E元件2009年1月—2011年6月水位、气压与应变相关系数曲线Fig.4 The N60E element’s correlation coefficient curves of strain and water level and atmospheric pressure at Liangping station in 2009.1—2011.6

气压和水位对应变值影响原理相似，故选取2008—2009年水位剧烈变化的16个时段和2010—2014年气压剧烈变化的33个时段同应变值，进行相关、回归分析（分析方法和原理同上文梁平台）。结果表明，同一元件不同时段水位、气压与应变的回归系数K接近（K表示气压每变化1 Pa，应变所对应的变化量，量纲为1/Pa），认为K真实反映该台应变与水位、气压关系的本构特性。4元件回归系数见表5、表7（只列出其中7段计算结果），由此可得各元件平均回归系数，见表6、表8，并得出相应关系式，见式（14）—式（17）、式（18）—式（21）。

由应变与水位的关系式得到垫江台四元件的关系式为

由应变与气压的关系式得到垫江台四元件的关系式

表5 垫江台不同时间段各元件观测值应变量与水位的相关系数R及回归系数KTable5 Correlation coefficient R and regression coefficient K of observed strain and water level of the elements at Dianjiang Seismic Station in different periods

表6 垫江新民台应变—水位回归系数KTable6 Regression coefficient K between strain and water level at Xingmin Seismic Station，Dianjiang

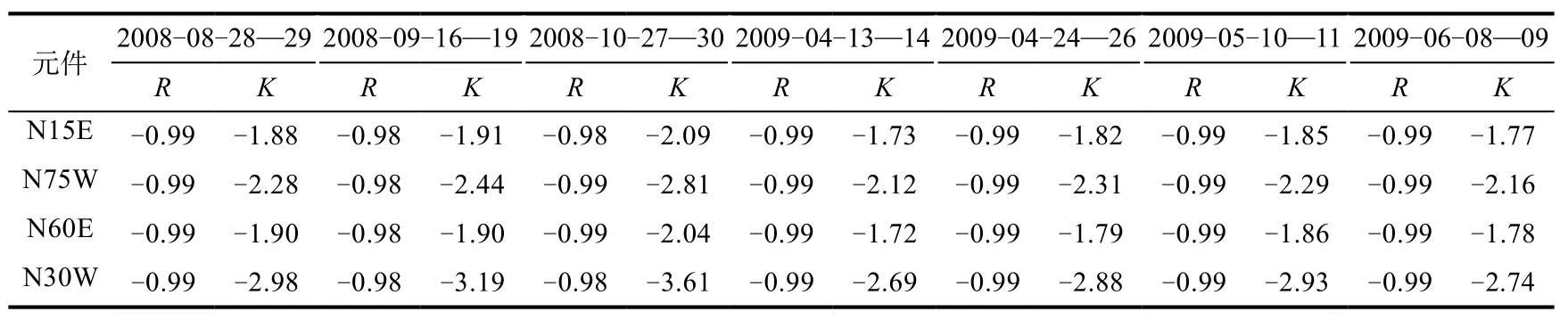
表7 垫江台不同时间段各元件观测值应变量与气压的相关系数R及回归系数KTable7 Correlation coefficient R and regression coefficient K between observed strain value and air pressure at Dianjiang Seismic Station in different periods

表8 垫江新民台应变—气压回归系数KTable8 Regression coefficient K between strain and atmospheric pressure at Xinmin Seismic Station，Dianjian

3 钻孔应变值水位（气压）改正

根据计算得出的应变与水位、气压关系式，求得经水位、气压改正的钻孔应变值，见图5—图7，其中（a）图为相应时间段应变整点值曲线，（b）图为经水位（气压）改正后的曲线。由图5可见，因水位影响造成的干扰明显减小，曲线更加平稳。由图6可见，因水位影响造成的干扰明显减小，曲线趋势更加平稳、光滑。由图7可见，应变曲线在滤除频率较高的气压干扰后更加光滑，噪声显著减小。

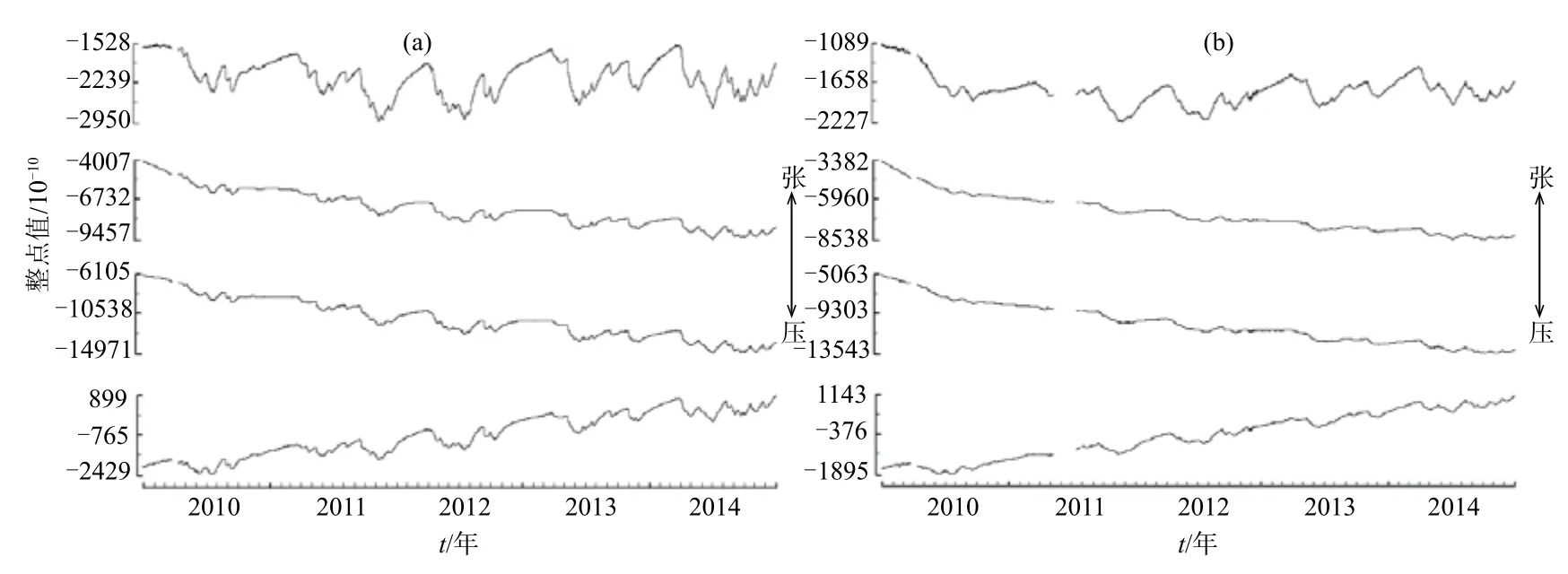
图5 梁平台2010—2014年应变整点值经水位改正前后曲线（a）原始应变整点值；（b）水位改正后应变整点值Fig.5 The hour mean value curves of strain before and after water level correction at Liangping Seismic Station in 2010-2014

图6 垫江台2009年应变整点值经水位改正前后曲线（a）原始应变整点值；（b）水位改正后应变整点值Fig.6 The hour mean value curves of strain before and after throuth water level correction at Dianjiang Seismic Station in 2009

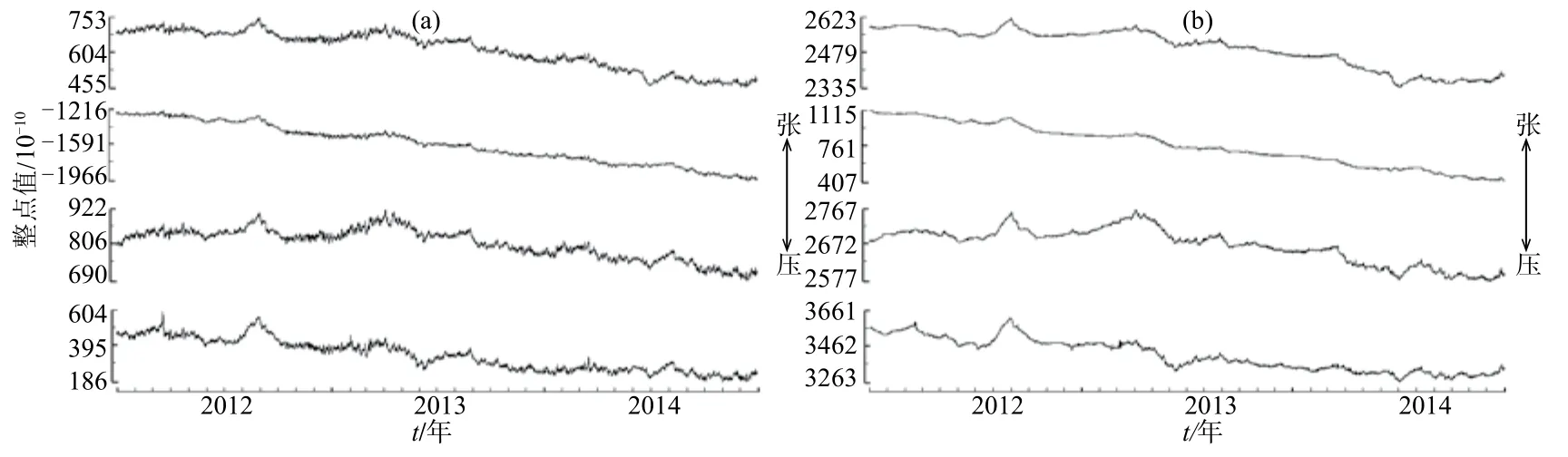
图7 垫江台2012—2014年应变整点值经气压改正前后曲线（a）原始应变整点值；（b）水位改正后应变整点值Fig.7 The hour mean value curves of strain before and after atmospheric pressure correction at Dianjiang Seismic Station in 2012-2014

4 结论

通过对重庆库区钻孔台站数据计算，定量分析各台水位（气压）与应变的关系和特征，认为在短时间段内，水位（气压）与应变回归系数真实反映二者的本构特性。利用得出的关系式，可以为梁平、垫江钻孔应变数据剔除水位（气压）干扰提供一种准确可行的方法。

分析发现，井孔所处地质构造、水文地质条件是影响钻孔水位数据质量的主要因素。在地下水丰富、岩层裂隙发育的钻井内，钻孔水位往往不稳定，数据质量较不理想。另外，破坏井孔地表结构、对钻孔井进行灌浆作业等均会影响或改变钻孔应变与水位的相关性。

本研究撰写得到唐小勇的精心指导和帮助，在此谨表谢意。

蒋静祥，唐小勇.水位相关斜率异常与地震的关系研究［J］.地壳形变与地震，1999，19（4）：68-74.

卢双苓，于庆民，曲保安，冯志军，李杰.山东数字化钻孔体应变观测的干扰异常分析［J］.西北地震学报，2010，32（2）：186-19.

马震，杜鹃，马玉虎.青海省钻孔应变资料典型干扰特征分析［J］.高原地震，2011，23（1）：53-58.

邱泽华，阚宝祥，唐磊.四分量钻孔应变观测资料的换算和使用［J］.地震，2009，29（4）：84-87.

唐小勇，王新刚，王文景，罗洪亮，曹卫东.乌鲁木齐台钻孔应变与水位相关性的初步研究［J］.内陆地震，2002，16（3）：244-251.

朱航.地下水位与应变的相关性分析［J］.内陆地震，2001，15（3）：247-251.

Preliminary research on the correlation of borehole strain and water level at the Three Gorge Sreservoir area of Chongqing Municipality

Li Guangke，Chen Kai and Gong Haobo
（Earthquake Administration of Chongqing Municipality，Chongqing 401147，China）

Since 2007，the earthquake administration of Chongqing Municipality set up multiple sets of high precision RZB-2 capacitive borehole strainmeters in Three Gorges Reservoir area.In order to study the relation between strain and water level，the correlation coefficient and regression coefficient of strain and water level were calculated using the sudden change of water level.It is thought that this relation can be used to remove the influence of water level on the observation value of strain.

borehole strain，correlation coefficient，regression coefficient，water level，atmospheric pressure

10.3969/j.issn.1003-3246.2015.05.010

李光科（1984—），男，重庆市江北区人，助理工程师，现从事重庆市地震台前兆、测震工作。E-mail：77938722@qq.com

重庆市地震局资助

本文收到日期：2015-04-13