HHT变换在地磁数据处理的应用

向 阳孙吉泽，赖爱京史勇军高小其张建国

1）中国乌鲁木齐830011新疆维吾尔自治区地震局

2）中国北京100086中国地震局地球物理研究所

3）中国新疆维吾尔自治区843000阿克苏中心地震台

4）中国河北056000邯郸中心地震台

HHT变换在地磁数据处理的应用

向 阳1）孙吉泽1），2）赖爱京3）史勇军1）高小其1）张建国4）

1）中国乌鲁木齐830011新疆维吾尔自治区地震局

2）中国北京100086中国地震局地球物理研究所

3）中国新疆维吾尔自治区843000阿克苏中心地震台

4）中国河北056000邯郸中心地震台

采用改进的EMD阈值进行分解，将地磁数据进行阈值滤波后重整；做频率域分析，认为EMD阈值滤波可以有效去除高频干扰，尽可能保留低频信息。对磁静日和磁扰日数据进行EMD消噪，做时频分析，在HHT谱和边际谱清晰呈现地磁信号的动态变化特征及对应的能量变化。

地磁；HHT变换；EMD分解；时频分析；阈值滤波

0 引言

大量观测表明，地震的孕育和发生伴随着电磁场的变化（韩鹏，2009；徐文耀，2009；邢西淳等，2005）。采用不同信号处理方法分析地磁信号，提取时频信息，发现数据中蕴含的有用信息是地震地磁学研究的重要内容之一。地震的孕育和发生是一个复杂的物理过程，相关的地震地磁物理机制目前还在探索；以往针对地磁信号的研究（张亮娥等，2007；吴利辉等，2009；谢凡，2012）证明，地磁信号中地震信息微弱，容易淹没在地磁背景场噪声中。因此，研究地磁数据中地震信息的提取方法具有重要意义。

Hilbert—Huang变换（HHT）是近年出现的一种自适应的非平稳、非线性信号处理方法，通过非平稳信号的线性化，建立以瞬时频率为表征信号变化的基本量，创造新的时频分析方法体系（李彦军等，2010），对于在地磁资料中提取有用的地震前兆信息具有重要意义。

1 HHT变换

HHT变换（NE Huang，1998），其核心是利用经验模态分解（EMD），依据自身的时间尺度定出源信号x（t）上的所有极值点，再利用拟合函数将极值点分别进行曲线拟合，得到上下包络线（图1），将两条包络曲线的平均值记为m，定义h=x（t）-m，将h视为新的源信号，重复操作直到h满足给定的终止条件时筛选终止，记c1= h，r =x（t）-c1，由此得到x（t）的分解式

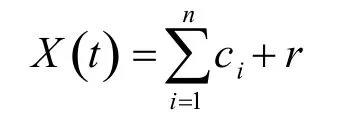
式中r为残余函数，代表信号的平均趋势。

图1 EMD分解示意Fig.1 The schematic diagram of Empirical Mode Decomposition

对给定的源信号x（t）的n阶IMF分量分别进行Hilbert变换，求得瞬时频谱，综合得到H（ω，t），对时间进行积分，获得信号的边际谱H（ω），即

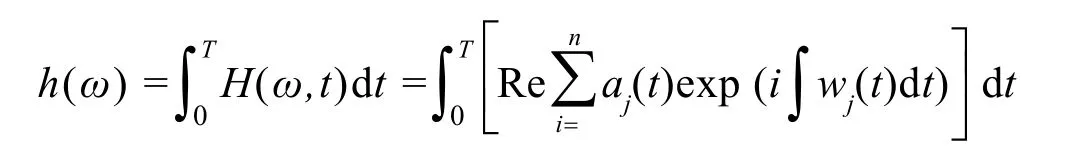
2 改进的EMD阈值消噪

传统的EMD去噪是将含噪的IMF分量在重构时排除，以达到去噪的目的，容易造成某些有价值的频率成分被舍弃。根据小波变化中的阈值去噪，对EMD分解后的IMF进行阈值去噪，去除噪声成分，可以最大程度保留原信号中的频率成分（Donoho D L et al，1995）。

经过EMD分解得到一个或几个IMF分量，按照一定条件滤除噪声，并保证有用信号的完整性。给定信号x（t）经EMD分解后得到n个IMF，对每一层IMF（C1-Cn）选择一个合适的阈值，对每个Ci进行截断，即，然后进行信号重构。

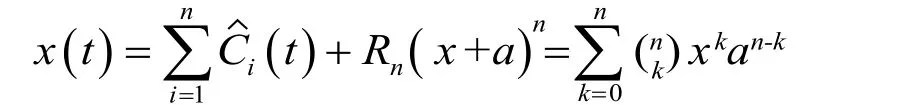
根据Donoho等（1995）的理论，消噪阈值为

式中，σi为第i层IMF的噪声水平，MADi为第i层IMF的绝对中值偏差，定义为

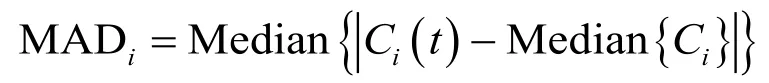
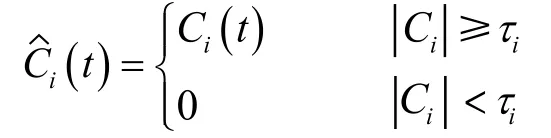
软阈值方法为

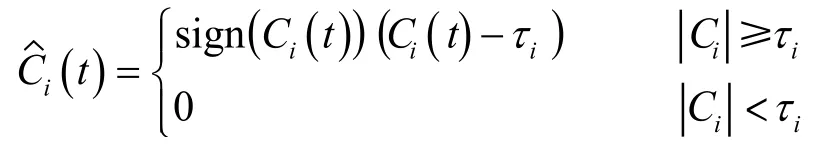
地磁信号去噪时选择软阈值进行处理，得到的波形更接近实际，而硬阈值处理信号比较粗糙。以乌什地震台地磁记录的单日分钟值数据［图2（a）］为例，通过EMD利用信号自身极值进行分解，将一个复杂的信号分解为n个有规律的本征模函数（IMF）和一个残余信号，反映源信号自身频率特征；对每个IMF分量进行软阈值去噪，进行重构，得到去噪后的信号［图2（b）］。为验证EMD阈值滤波的有效性，通过傅里叶变换，对比消噪前后傅里叶谱（图3），结果发现，前后频率无太大差别，优势频率集中在低频段，说明消噪去除高频影响，而对低频段未造成损失，可以作为对干扰抑制效果的一种评判。

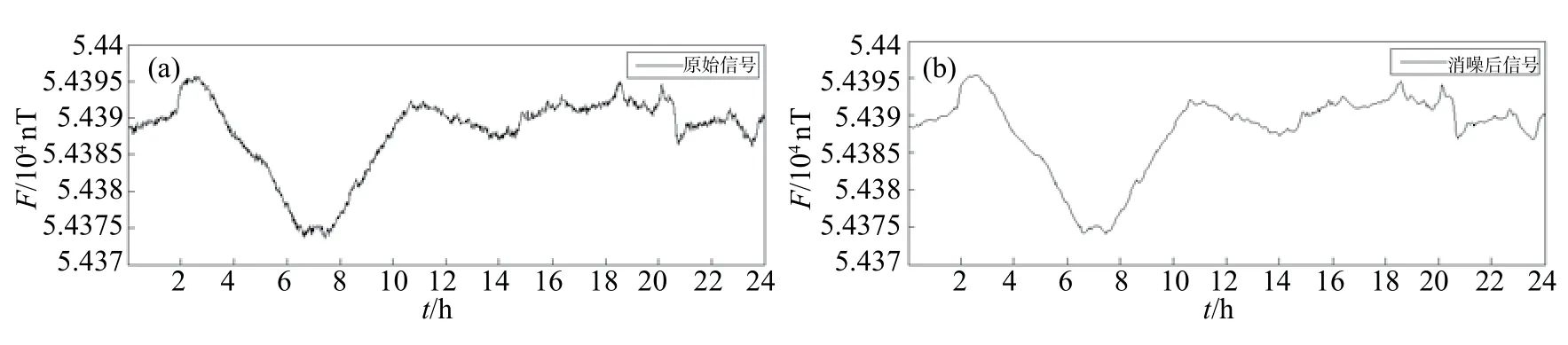
图2 乌什台地磁分钟值EMD阈值消噪（a）乌什台地磁分钟值数据；（b）EMD阈值消噪后重构数据Fig.2 Reconstructed data by EMD threshold fltering at Wushi Seismic Station

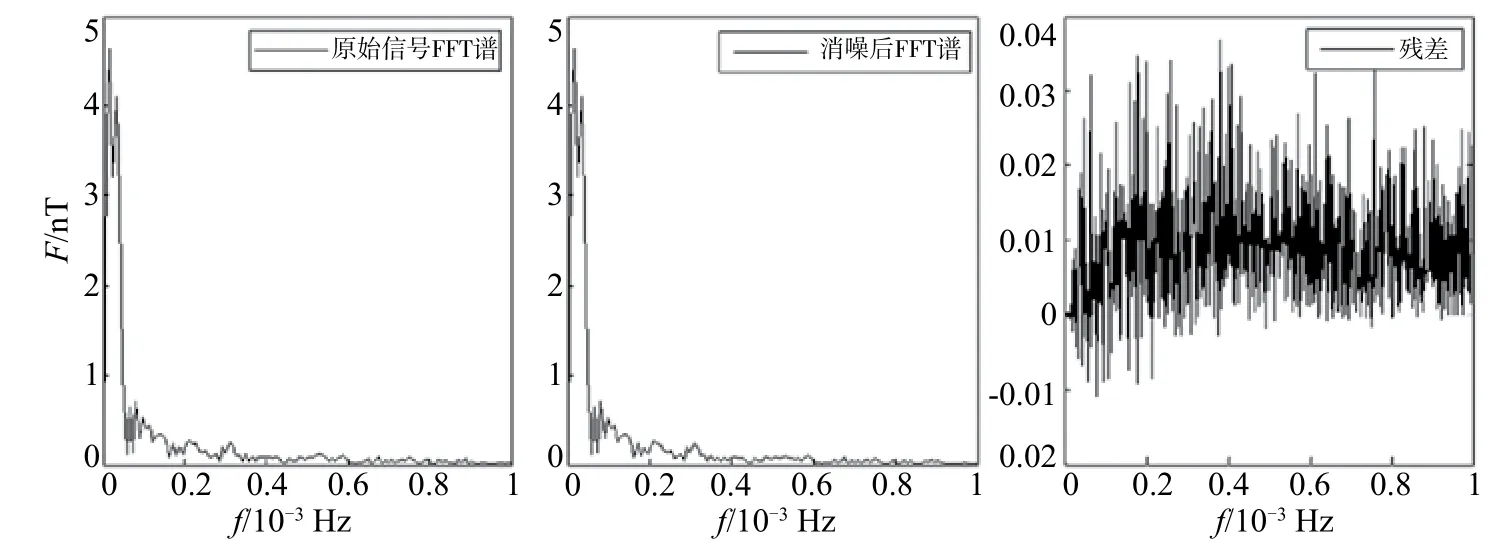
图3 消噪前后傅里叶谱比较Fig.3 The compare of FFT spectra with original data and de-nosing data

3 HHT变换分析

地磁信号各频率成分是分段甚至毫无规律的，建立在稳态信号处理基础上的傅里叶变换必须采用额外的谐波分量来弥补或均衡，采用该方法估计频谱势必带来偏差，造成信号能量泄漏，无法反映各个时段上的频谱变化特征。HHT方法能很好地刻画地磁信号的动态变化特征，信号的每个突跳、持续时段和频带分布能够清晰呈现出来。从时频谱可以看出频率成分及能量变化。选取磁静日和磁扰日连续3天数据，对比分析HHT时频谱。

对磁静日信号消噪后，做HHT时频谱和边际谱分析，见图4。从时频谱上可以看出，通过EMD阈值消噪只是将源信号中蕴含的噪声信号去除，剩余的日变长周期信息保留下来。时频谱中清楚显现信号各时段的不同频率，从边际谱也可以看出信号中存在的优势频率范围（图4），可用于日常地磁数据筛选。

对磁扰日信号，进行消噪处理和时频分析，见图5，可以看出，时频谱能较好反映原始信号中高频干扰时间段。

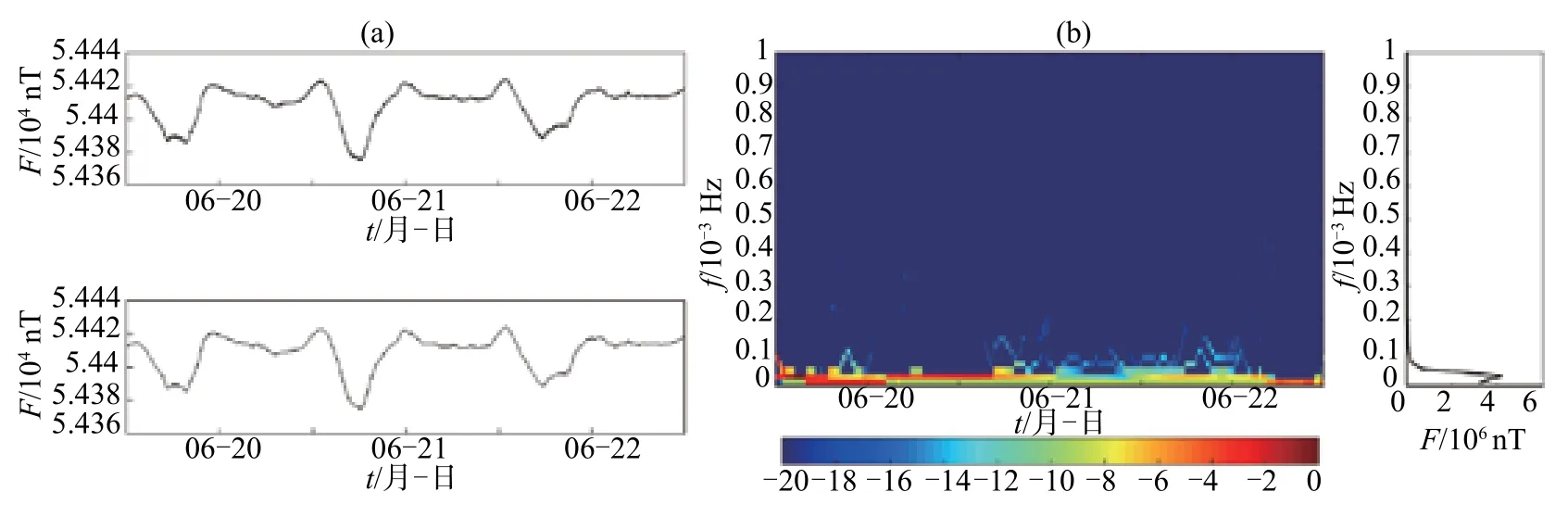
图4 磁静日地磁信号HHT时频谱和边际谱（a）消噪前后信号；（b）消噪后HHT时频谱和边际谱Fig.4 HHT spectrum and marginal spectrum of data of magnetically quiet day

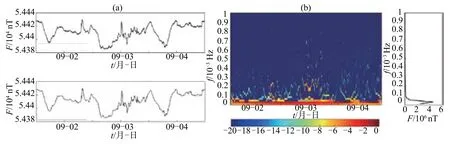
图5 磁扰日地磁信号的HHT时频谱和边际谱（a）磁扰日消噪前后信号；（b）消噪后磁扰日地磁信号的HHT时频谱和边际谱Fig.5 HHT spectrum and marginal spectrum of data of magnetically disturbed day

3 结论

随着断层蠕动和岩体变形，地下压电岩体由于压电效应产生一定电场或磁场，当能量足够大时，被地磁仪记录下来而成为地磁信号中的地震信息，这些信号往往比较微弱且频率较低，容易淹没在地磁背景场噪声中。地磁数据分析是地磁学研究基础，选择合适的分析方法提取信号主要特征，对识别信号中的地震前兆信息意义重大。利用HHT方法，对新疆乌什地震台地磁数据进行消噪处理和频谱分析，得到以下结论。

（1）采用EMD分解，分解地磁数据信号，通过阈值滤波后进行重整，结果与原信号在频率域上比较接近，说明EMD阈值滤波，消噪效果较好，可尽量保留原信号的优势频率成分。

（2）通过对磁静日和磁扰日数据进行消噪处理和时频分析，在HHT频谱中，清楚可见地磁信号的动态变化特征，频谱中信号的每个突跳、持续时段、能量变化和频带分布能够清晰呈现出来。

随着经济发展，地磁台站越来越受到场源的扰动、环境和噪声的干扰，地磁数据中伴随大量噪声和干扰信号，呈现非稳定、非线性特征，利用HHT方法，在地磁数据处理中引入EMD滤波方法，可以有效提高信号利用率，增强数据处理质量。从时频谱上对信号进行分析，寻找大震前信号频谱的相关变化规律和异常特征，以期能将地磁信号更好地用于地震预报。

安张辉，元丽华，等.HHT方法在地电场数据处理中的应用［J］.地球物理学进展，2010，25（2）：525-532.

蔡剑华，汤井田，等.基于Hilbert—Huang变换的大地电磁信号谱估计方法［J］.石油地球物理学报，2010，5（5）：762-767.

蔡剑华.基于Hilbert—Huang变换的大地电磁信号处理方法与应用研究［D］.中南大学，2010.

曹志磊，周琼，等.蒙城地震台地磁Z分量日变化特征分析［J］.地震地磁观测与研究，2008，29（5）：48-51.

韩鹏.地震地磁数据处理方法研究［D］.中国地震局地球物理研究所，2009.

李彦军，胡祥云，等.HHT变换在地球物理中的应用现状及前景［J］.工程地球物理学报，2010，7（5）：537-544.

汤井田，化希瑞，等. Hilbert—Huang变换与大地电磁噪声压制［J］.地球物理学报，2008，51（2）：603-610.

汤井田，蔡剑华，等.Hilbert—Huang变换与大地电磁信号的时频分析［J］.中南大学学报（自然科学版），2009，10（5）：1 399-1 405.

吴利辉，滕云田，等.南京地磁台地铁干扰特征分析与抑制处理［J］.地震地磁观测与研究，2009，30（6）：32-39.

谢凡.地磁观测中干扰抑制方法的发展及展望［J］.地球物理学进展，2012，27（3）：967-976.

解用明，武连祥，等.地磁Z分量日变化特征［J］.地震地磁观测与研究，2004，25（1）：52-56.

熊学军，郭炳火，胡筱敏，等.EMD方法和Hilbert谱分析方法的应用与讨论［J］.黄渤海海洋，2002，20（2）：12-21.

邢西淳，邵辉成，等.小波变换在地磁数据分析中的应用［J］.地震地磁观测与研究，2005，26（2）：38-42.

徐文耀.地球电磁现象物理学［M］.合肥：中国科学技术大学出版社，2009

杨培杰，印兴耀，张广智，等.希尔伯特—黄变换地震信号时频分析与属性提取［J］.地球物理学进展，2007，22（5）：1 585-1 590.

张亮娥，殷志刚，等.太原郝庄5.0级地震前后地磁异常研究［J］.地震地磁观测与研究，2007，28（6）：24-31.

D L Donoho.De-noising by soft-thresholding［J］.IEEE transaction on information theory，1995，41（3）：613-627.

D L Donoho，I MJohnstone et al.Wavelet Shrinkage: Asymptopia？［J］.Journal of the Royal Statistical Society，1995，57（2）：301-369.

NE Huang，Z Shen，SR Long et al.The empirical mode decomposition and the Hilbert Spectrum for nonlinear and

non-stationary time series analysis［J］.Royal Society of London Proceedings，1998，454（1 971）：903-995.

Application of HHT method in geomagnetic data handling

Xiang Yang1），Sun Jize1），2），Lai Aijing3），Shi Yongjun3），Gao Xiaoqi1）and Zhang Jianguo4）
1） Earthquake Administration of Xinjiang Uygur Autonomous Region，Urumqi 830011，China
2） Institute of Geophysics，China Earthquake Administration，Beijing 100081，China
3） Akesu Central Seismic Station，Xinjiang Uygur Autonomous Region 843000，China
4） Handan Central Seismic Station，Hebei Province 056000，China

Using the modified EMD threshold method，geomagnetic data is de-noised by threshold method and then reconstructed.By analysis in frequency domain，EMD threshold method is more effective in de-noise high frequency interference from the low frequency information.After denoising by EMD method，we make time frequency analysis to the data of magnetically quiet day and disturbed day.And the result of HHT spectrum and marginal spectrum displayed the change of dynamic frequency characteristics of geomagnetic data and the change of energy clearly.

geomagnetism，HHT，EMD，time frequency analysis，threshold flter

10.3969/j.issn.1003-3246.2015.05.009

向阳（1989—），女，助理工程师，毕业于喀什师范学院物理系，主要从事地下流体监测、 预报和科研工作

国家自然科学基金（41274079）、财政部行业专项（201408008）和新疆地震科学基金（201309） 联合资助

本文收到日期：2014-07-29