定积分的背景:面积和路程问题
2015-11-15王瑰丽
王瑰丽
(陕西省宝鸡市凤翔县彪角中学)
一、教学内容分析
课题:定积分的背景—面积和路程问题
课型:新授课
教材:《普通高中课程标准数学教科书·数学选修2-2》(北师大版)
教材分析:本节的主要内容是展现定积分的实际背景,形成定积分的概念。教材设计了3个实例:求曲边梯形的面积、根据物体运动的速度求路程、求物体拉力做的功。通过这些问题的解决,总结这些问题的解决思路:即通过分割求和、加细、减小误差,然后再提高精确度的过程,这个过程是定积分思想的核心,为定积分概念的引入奠定了背景和方法的基础。
二、学情分析
从学生的思维特点看,会从物理角度对问题进行解决。这是积极因素,应因势利导。
教学对象是学生,虽然经过一年多的高中数学学习,具有一定的分析问题和解决问题的能力,逻辑思维能力也初步形成,但思维尽管活跃、敏捷,却缺乏冷静、深刻,因此片面、不严谨。
三、设计思想
《新课程改革纲要》提出,要“改变课程实施过于强调接受学习、死记硬背、机械训练的现状,倡导学生主动参与、乐于探究、勤于动手,培养学生搜集和处理信息能力、获取新知识的能力、分析和解决问题的能力以及交流合作的能力”。对这一目标本人认为更加注重培养学生作为学习主体的能动性、独立性、创造性、发展性。
四、教学目标
1.知识与技能:(1)了解定积分的实际背景。
(2)借助几何直观体会定积分的基本思想,初步了解定积分的概念。
2.过程与方法:通过洞察不同背景问题中蕴涵的相同数学内涵的过程,领会如何先考虑得到近似解,然后再研究提高精确程度的定积分的解决问题的基本方法,提高从数学角度分析和看待问题的能力。
3.情感、态度与价值观:通过对不同背景下的问题用统一数学方法的揭示,认识数学与实际生活的联系,以及数学的广泛应用。
五、教学重点与难点
1.教学重点:对实际问题解决的分析(即如何通过分割、求和、取极限求出曲边梯形面积和变速直线运动物体的路程),这个过程是积分思想的灵魂。
2.教学难点:例题的分析及解题思路的总结提炼。
六、教学工具
借助多媒体
七、教学过程
(一)创设情境,提出问题
我们学过如何求正方形、长方形、三角形等的面积,这些图形都是由直线段围成的。那么,如何求曲线围成的平面图形面积呢?
1.曲边梯形定义
我们把如图由直线x=a,x=b(a≠b),y=0和曲线y=f(x)所围成的图形叫曲边梯形。
曲边梯形概念的理解:
(1)曲边梯形是由曲线段和直线段所围成的平面图形。
(2)曲边梯形与“直边图形”主要区别在于前者有一边是曲线段而“直边图形”的所有边都是直线段。
2.问题提出
问题1图中阴影部分由抛物线y=x2,直线x=1及x轴围成的平面图形,试估计这个曲边梯形的面积S。
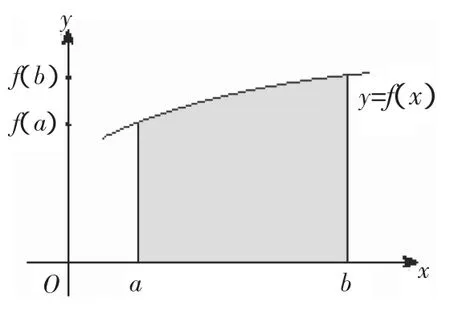
图1

图2
(二)操作探究
活动1:方案提出
引导学生回顾曾经用正多边形逼近圆的方法(即“以直代曲”的思想)求出了圆的面积,让学生初步形成“以直代曲”的思想,在具体“以直代曲”的过程中能通过小组讨论的方式提出多种方案。
活动2:方案落实
方案落实1:将区间[0,1]平均分成5份,如图所示。
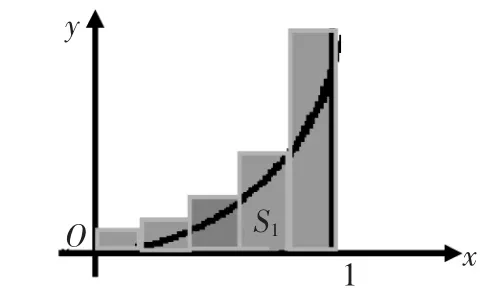
图3

图4
在图3中所有小矩形的面积之和S1显然大于所求曲边梯形的面积,我们称S1为S的过剩估计值,在图4中所有小矩形的面积之和S1显然小于所求曲边梯形的面积,我们称S1为S的不足估计值,有 S1=(0+0.22+0.42+0.62+0.82)×0.2=0.24
我们可以用s1或S1近似表示S,但是都存在误差,二者之差为S1-s1=0.2,但是无论是用s1还是S1来表示曲边梯形的面积,误差都不会超过0.2,如图5所示。
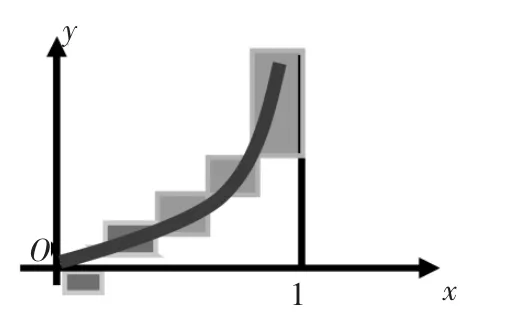
图5
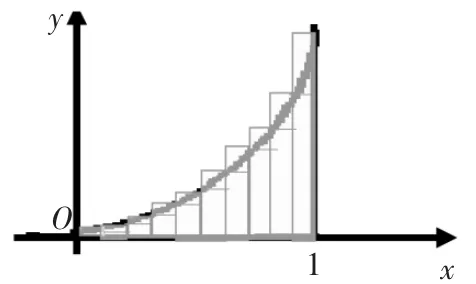
图6
方案落实 2:为减小误差,我们将区间[0,1]10等分,则所求面积的过剩估计值为 S2=(0.12+0.22+…+12)×0.1=0.385的解决过程是相似的,都是通过分割自变量的区间得到过剩估计值和不足估计值,分割的越细,估计值就越接近精确值;当分割成的小区间的长度趋于0时,过剩估计值和不足估计值都趋于要求的值。)
(三)初步应用
1.计算直线x=0,x=1,y=0和曲线y=x3围成的阴影图形的面积。
2.火箭发射 t s 后的速度为 v(t)(单位:m/s),假定 0,对函数v(t)按上式所做的和具有怎样的实际意义?
(四)小结
本节课主要内容是展现定积分的实际背景,通过对实际问题的求解总结出这类问题的解决思路,即通过分割—以直代曲—作和—逼近。
(五)课后作业习题4-1 A组1,2,3
不足估计值为 S2=(02+0.12+0.22+…+0.92)×0.1=0.285
二者的差值为S2-S2=0.1,此时,无论用S2还是S2来表示S,误差都不超过0.1。
活动3:探究总结
将区间[0,1]平均分成许多小区间,把曲边梯形拆分成一些小曲边梯形,对每个小曲边梯形“以直代曲”,即用矩形面积近似代替小曲边梯形的面积,得到每个小曲边梯形的面积,对这些近似值求和,就得到曲边梯形面积的近似值。
可以想象,区间拆分的越细,近似程度就越好,亦即:用化归为计算矩形面积和逼近思想来求曲边梯的面积。可通过以下几个步骤具体实施:(1)分割;(2)近似代替(过剩和不足估计值);(3)逼近。
活动4:动手实践
(1)司机猛踩刹车,汽车滑行5 s后停下,此过程中汽车的速度 v 是时间 t的函数:v(t)=t2-10t+25(0≤t≤5)
请估计汽车在刹车过程中滑行的距离s。
(2)做功问题:一根弹性系数0.4N/cm的弹簧,其拉力F=F(x)=0.4x。弹簧的一端固定在墙上,另一端固定在物体上,在不考虑摩擦的情况下物体在力F作用下匀速移动,从原来位置移动10 cm。估计这一过程中拉力所做的功。
(此过程让学生自己完成,让学生体会:在上面的讨论中,面积问题、路程问题以及做功问题是三个实际意义完全不同的问题,但他们
八、板书设计

1.1定积分的背景—面积和路程问题(一)创设情景,提出问题1.曲边梯形的定义2.问题提出(二)操作探究1.方案落实2.探究总结3.动手实践(三)初步应用
