数理统计方法在海浪灾害特征分析中的应用

任姝彤，张滨

（1.中国海洋大学，山东青岛 266100；2.国家海洋环境预报中心，北京 100081）

1 引言

中国地处欧亚大陆东南岸并与太平洋相通，南北冷暖气流异常活跃[1]，是世界上海浪灾害发生最频繁地区之一，冬季受西伯利亚、蒙古等地冷空气影响，春秋季受温带气旋影响，夏季受台风影响[2]，中国近海4 m以上灾害性海浪过程全年频发。研究表明海上自然破坏力的90%来自海浪，海浪灾害可沉损船只，是海难事故的最主要原因，同时海浪灾害还可摧毁沿岸各类建筑物，它会对航海、海上施工、海上军事活动、渔业捕捞等带来极大危害，是海上经济开发的最大障碍[3]。1990据国家科委全国重大自然灾害综合研究组粗略的统计，我国近海由海浪引起的海难每年平均有70次，损失每年约1亿元，死亡约500人[4]。据《中国海洋灾害公报》统计2013年我国近海共出现43次灾害性海浪过程，造成直接经济损失6.30亿元，死亡（含失踪）121人。近10 a来，灾害性海浪共造成直接经济损失34.47亿元，造成人员死亡（含失踪）1147人[5]。

灾害性海浪的研究方面，管长龙等[6]回顾和总结20世纪80年代初至90年代末我国学者在海浪要素统计分布上进行的研究；杨良华[3]对中国沿海由于热带气旋、温带气旋和强冷空气影响下的海浪活动强度和分布情况进行研究；孙璐等[7]对广海湾内海浪基本要素以及大浪过程与热带气旋活动的关系进行统计分析；张薇等[8]利用渤海周边10个波浪观测站46 a的海浪观测资料,进行了灾害性海浪特征分析和海浪致灾原因分析,给出了渤海灾害性海浪的时、空变化和分布特征,并对海浪灾害致灾原因进行天气学分析。统计方法是海浪研究的一种重要手段，国家海洋环境预报中心海浪组每年都依据有效波高≥4 m的灾害性海浪的历史数据,结合未来副热带高压及热带风暴的分析预测资料,预测下一年海浪灾害活动强度[9-12]，本文通过数理统计方法分析1968—2013年中国近海4 m以上灾害性海浪过程数据样本，对其统计规律进行描述，并使用回归分析法对灾害性海浪过程数进行多年趋势预测。

2 方法说明

数理统计方法主要包括描述性统计方法和推论性统计方法两类，前者是对数据的整理和描述，后者则通过样本数据信息推断总体。本文通过描述性统计方法对中国沿海灾害性海浪年过程数、灾害性台风浪年过程数、灾害性冷空气和气旋浪年过程数的统计规律进行描述，通过利用集中趋势分析、离散趋势分析以及频率分布情况描述灾害性海浪过程年际变化趋势；通过推论性统计方法中的单因子回归分析方法预测中国沿海灾害性海浪年过程数长期变化趋势。其中，集中趋势分析包括计算中国近海灾害性海浪过程、灾害性台风浪过程、灾害性冷空气气旋浪过程46 a平均值和总体均值，二者分别说明46 a间中国近海上述海浪灾害的一般水平以及更长时间范围内中国沿海上述海浪灾害的一般水平；离散趋势分析包括计算中国近海灾害性海浪过程、灾害性台风浪过程、灾害性冷空气气旋浪过程的全距（极差），标准差和离散趋势，表征了中国近海上述海浪灾害年际数据的分散性；频率分布分析利用频率直方图直观的表达中国近海上述海浪灾害灾情程度以及分布情况。

本文还引入了标准分数的概念，其用途是对比两组不同均值，不同标准差的数据样本中的特定数据，并判定他们在各组中的位置，在本文中用以对比特定年份灾害性台风浪过程和灾害性冷空气气旋浪过程的严重程度。

推论性统计方面，本文采用回归分析方法对样本灾害性海浪过程数据进行拟合，本文分别采用一元三次方程模型，和ARIMA模型对中国沿海灾害性海浪年过程数进行长期预测，其中：ARIMA（p，d，q）模型全称为差分自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA)可表示为:

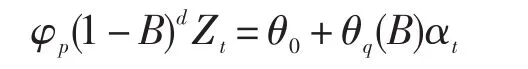
式中，Zt为原序列，αt为白噪声序列，是一列相互之间无关，其均值为0，方差为σ2的随机变量序列；B为后移算子即BZt=Zt-1；φp为自回归算子；P为模型的自回归除数；θq为移动平均算子；q为模型的移动平均阶数；θ0为参数[10]。

3 中国近海灾害性海浪过程统计分析

中国近海灾害性海浪大体可划分为灾害性冷空气气旋浪和灾害性台风浪两类，根据图1中国近海灾害性海浪过程46 a年际变化曲线分析，中国近海灾害性冷空气气旋浪过程数的年际变化曲线波动较大，并直接导致了中国近海灾害性海浪过程总数年际变化波动显著，1972年中国近海灾害性海浪过程出现25次，为46 a最小值，标准分数为-2.05，当年灾害性冷空气气旋浪过程数14次，标准分数-1.73，灾害性台风浪过程数11次，标准分数-1.41。1972年中国沿海海浪灾害为46 a最轻，冷空气气旋浪灾害和台风浪灾害较常年偏轻，相对于台风浪灾害，当年冷空气气旋浪灾害更严重；1980年灾害性海浪过程出现71次，为46 a最大值，标准分数3.31，当年灾害性冷空气气旋浪过程数51次，标准分数3.31，台风浪过程数20次，标准分数1.51。1980年是46 a中海浪灾害最严重年份，也是冷空气气旋浪灾害最严重年份，但台风浪灾害虽较常年偏重但轻于前者。总体来看，20世纪60年代末期到70年代中期，中国近海灾害性海浪过程出现次数少于70年代末期到80年代末期，进入90年代后，中国近海灾害性海浪过程数基本呈现4—6 a的周期性波动。

通过对46 a中国近海灾害性海浪过程样本数据进行描述性统计，46 a间中国沿海灾害性海浪过程总数达到1962次，平均每年发生42.61次，总体均值与样本均值偏差为2.97%，可以得出中国沿海平均每9 d会出现一次4m以上灾害性海浪过程；46年间中国沿海冷空气气旋浪过程总数达到1256次，平均每年发生27.3次，总体均值与样本均值偏差4.14%，可以得出中国沿海平均每13天会出现一次灾害性冷空气或气旋浪过程；46 a间中国沿海共发生灾害性台风浪过程706次，平均每年发生15.35次，总体均值与样本均值偏差2.96%，可以得出中国沿海平均每23 d出现一次灾害性台风浪过程。

由图1可以看出，中国沿海灾害性台风浪过程曲线变化较平稳，其全距可以代表数据的分散程度，但灾害性冷空气气旋浪过程曲线波动剧烈，极端值对全距影响较大，不能反映数据的分散程度。根据表1数据可以看出，灾害性冷空气气旋浪过程数与灾害性台风浪过程数差异巨大，二者标准差受样本数据本身影响较大，为了更准确的比较中国沿海灾害性台风浪过程和灾害性冷空气气旋浪过程的差异程度，使用离散系数（CV）进行分析，可以发现中国沿海灾害性冷空气气旋浪过程数据分散程度小，其过程数各个年份差异较大，灾害性台风浪过程数据分散程度小，其过程数各个年份差异较小，二者对比，灾害性台风浪年过程数较为集中的分布在均值周围，出现较大偏离值的概率更小，因此对灾害性台风浪过程的预测准确率可能更高。

图2给出了中国近海灾害性冷空气气旋浪过程、灾害性台风浪过程以及灾害性海浪总过程数的频率分布直方图，可以看出灾害性海浪总过程数变化幅度大，时间序列稳定性较差，频率呈尖峰态、左偏态分布，说明1968—2013年间，虽然多数年份灾害性海浪年过程数少于平均值42.61次/年，但偏差较小，46 a中，趋近年过程数极大值和年过程数极小值的年份也较少；灾害性冷空气和气旋浪过程数变化幅度较大，时间序列稳定性较差，年过程数少于均值过程数的年份略少于年过程数多于均值过程数的年份，但趋近于最大年过程数和最小年过程数的年份数量较多；灾害性台风浪过程变化幅度最小，但时间序列仍不稳定，多数年份年台风浪过程数少于均值过程数。

根据上文对中国近海灾害性冷空气气旋浪过程、灾害性台风浪过程以及灾害性海浪总过程数的频率分布分析，如果认为超过46 a灾害性海浪过程数平均值的年份为海浪灾害偏重灾年，未超过为偏轻灾年，通过图2可以直观的看出，灾害性冷空气气旋浪过程频率直方图中出现了频率曲线右侧尾部以外的柱形标志，且与灾害性海浪总过程频率直方图一致，说明冷空气气旋浪灾害出现过极重灾年，且直接导致当年中国近海海浪灾害为极重灾年。

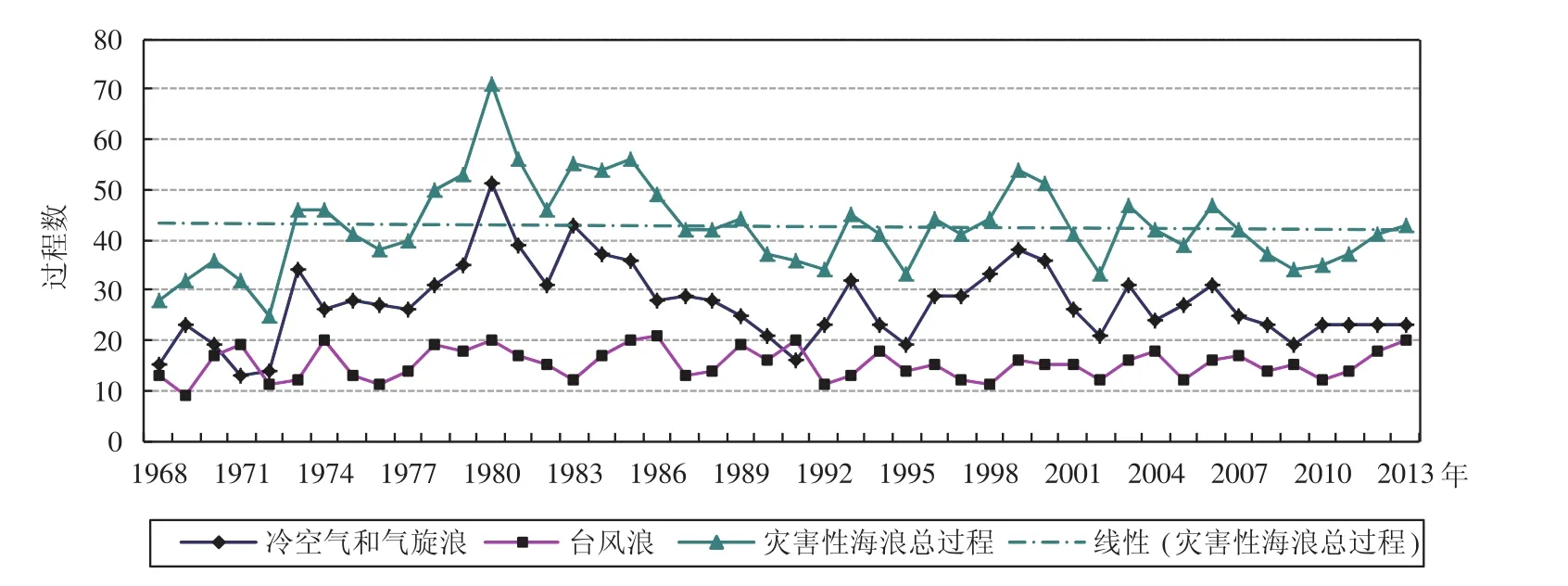
图1 中国近海灾害性海浪过程年际变化

表1 1968—2013年中国近海灾害性海浪过程描述性统计量

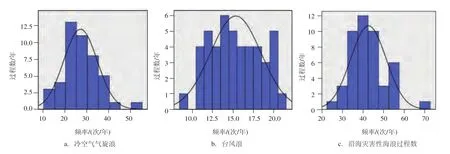
图2 1968—2013年中国沿海灾害性海浪过程频率分布直方图

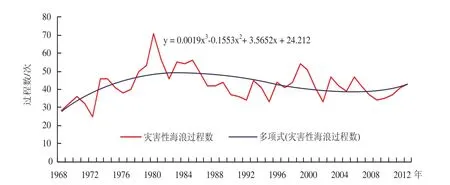
图3 中国近海灾害性海浪过程数一元三次方程模型拟合图

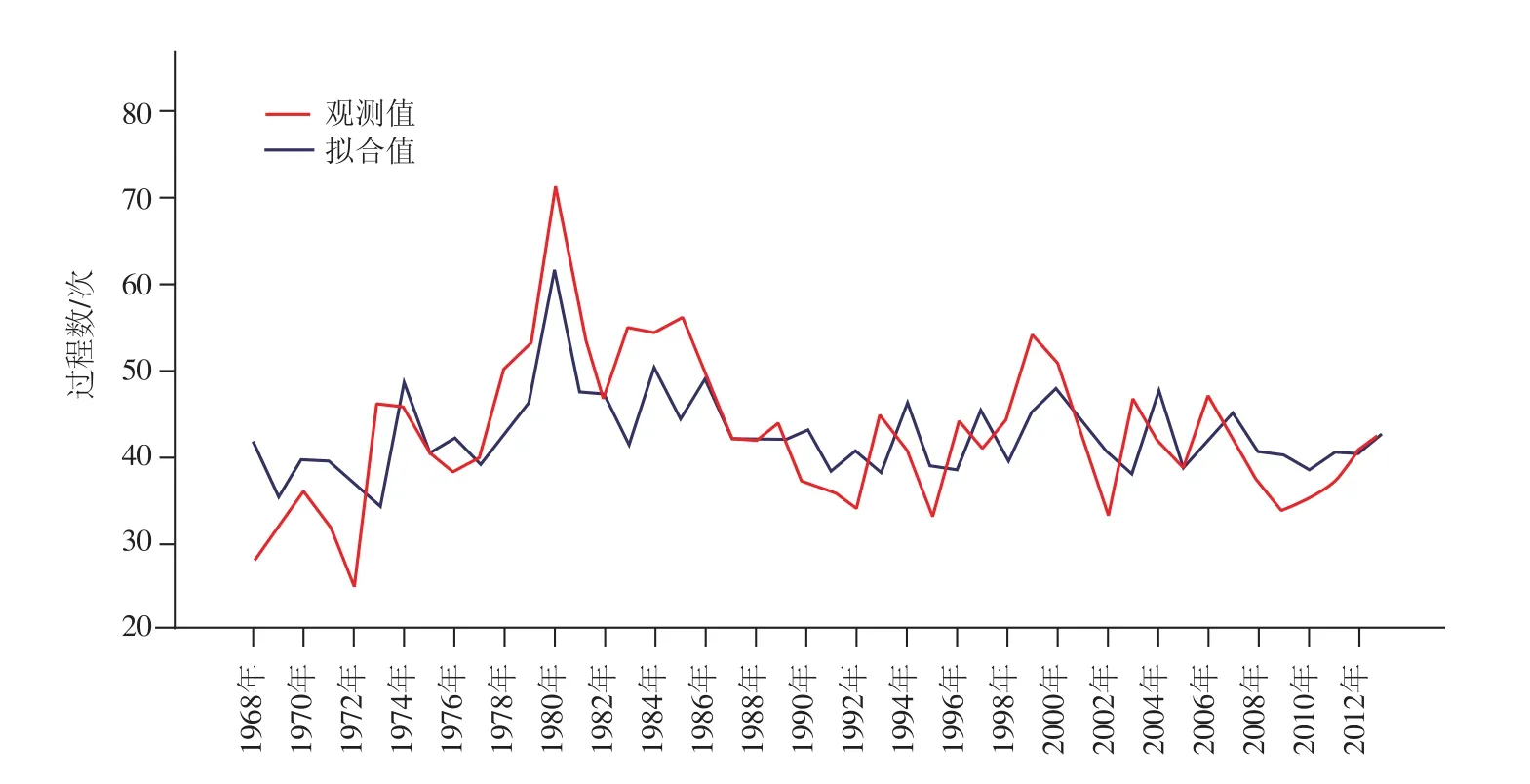
图4 中国近海灾害性海浪过程数ARIMA模型拟合图

根据已得到的中国近海灾害性海浪过程分布特征，引入回归分析方法对中国近海灾害性海浪过程进行预测，分别使用一元三次模型和ARIMA模型进行拟合，将中国近海灾害性海浪过程数时间序列进行指数平滑，依据最小信息量原则选择ARIMA(0，0，1)做原序列预测的最优模型，见图3、图4所示，一元三次方程模型相关系数为0.3448，ARIMA（0，0，1）模型相关系数为0.444，从相关性上比较，ARIMA模型拟合效果更好。

对上述两种模型的预测值进行比较，对于4年数据值，虽然2种模型对变动趋势的预测都为正向，但ARIMA模型相对误差较小，并且如前文描述性统计结论所述，中国沿海灾害性海浪过程年际变化波动显著，对比图3、图4可以看出，ARIMA模型对灾害性海浪过程数年际变化的波动性拟合明显优于一元三次方程模型。

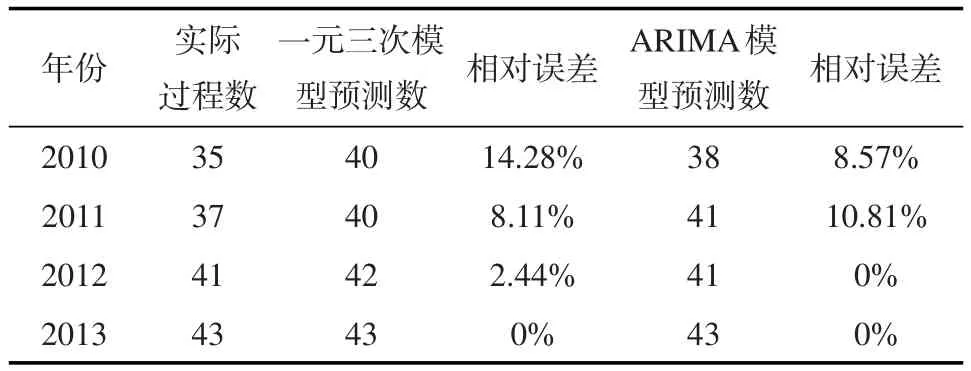
表4 两种模型预测值的比较

4 结论

中国近海灾害性海浪过程频发，平均年过程数大约在40—43次，呈4—6 a周期性波动趋势，其中冷空气气旋浪过程数远高于台风浪过程数，平均每9 d会出现一次4 m以上灾害性海浪过程，平均每13 d会出现一次灾害性冷空气气旋浪过程，平均每23 d出现一次灾害性台风浪过程。灾害性台风浪过程年际变动范围小于冷空气气旋浪年际变动范围，相对更加稳定，偏轻灾年较多，没有出现极重或极轻灾年；冷空气气旋浪过程数年际变动幅度极大，偏重灾年年份较多，既出现过极重灾年，也出现过极轻灾年。结合推论性统计和描述性统计对灾害性海浪过程样本数据分布情况的描述，可以考虑使用ARIMA模型对其时间序列进行预测，得到灾害性海浪年际变化规律趋势。

[1]许富祥,余宙文.中国近海及其邻近海域灾害性海浪监测和预报[J].海洋预报,1998,15(3):63-68.

[2]冯士筰,李凤歧,李少菁,等.海洋科学导论[M].北京:高等教育出版社,1999.

[3]杨良华.主要天气系统影响下中国沿海的海浪分布[J].航海技术,2002,(2):31-32.

[4]叶涛,郭卫平,史培军.1990年以来中国海洋灾害系统风险特征分析及其综合风险管理[J].自然灾害学报,2005,14(6):65-70.

[5]国家海洋局.中国海洋灾害公报[R].1989-2013.

[6]管长龙.我国海浪理论及预报研究的回顾与展望[J].青岛海洋大学学报,2000,30(4):549-556.

[7]孙璐,黄楚光,蔡伟叙,等.广海湾海浪要素的基本特征及典型台风过程的波浪分析[J].热带海洋学报，2014,33(3):17-23.

[8]张薇,高山,阉忠辉,等.渤海灾害性海浪特征分析[J].海洋预报,2012,29(5):73-77.

[9]许富祥.一种台风浪长期预测方法的探讨[J].海洋预报,1995,12(2):67-73.

[10]许富祥.1998~2002年海洋灾害与减灾[J].海洋预报,2004,21(2):9-13.

[11]邢闯,李本霞.中国近海2012年灾害性海浪分析及2013年预测[J].海洋预报,2013,30(3):1-8.

[12]王红瑞,康健,林欣,等.水文序列ARIMA模型应用中存在的问题与改进方式[J].系统工程理论与实践,2008,(10):166-176.