东中国海潮流结构数值模拟与分析
2015-11-14褚芹芹张鑫孙佳
褚芹芹,张鑫,孙佳
(1.国家海洋局秦皇岛海洋环境监测中心站,河北秦皇岛 066002;2.河海大学港口海岸与近海工程学院,江苏南京 210098)
1 引言
近些年来,关于东中国海潮流的数值研究工作颇为普遍。Guo等[1]通过三维海流数值模式的模拟结果分析了垂向湍粘性系数和底摩擦系数的变化对东中国海潮流垂向分布的影响;王凯等[2]利用了球面坐标系下的半隐半显三维数值模式,详细的分析了东中国海的潮流垂向结构并首次提出了圆流点的水平位置不随深度变化的特征;Jong Chan Lee等[3]认为如果底摩擦系数取值接近于近底层的涡动粘性系数,潮流的模拟结果会更加准确;Bao等[4]使用了三维湍封闭的模式对东中国海的M2、S2、K1和O1四个主要分潮流的特征进行了分析和讨论。
关于潮流的垂向结构及其分布特征,方国洪[5]做了详细的研究,认为在深度接近海底时,潮流流速的最大值会逐渐减小,但潮流椭圆率反而随着接近海底逐步增加。叶安乐[6]的研究结果反映了潮波角频率σ和科氏参量f两个参数的取值决定了潮流最大流速的流向变化和潮流最大流速发生时间的变化。
2 模型与数据介绍
2.1 模型设置
本文采用FVCOM(Finite Volume Coast and Ocean Model)海洋数值模式[7],计算区域为 17°—42°N,116°—136.5°E,包括了渤海、黄海、东海、日本海和南海的部分海域。在水平方向上采用了可变分辨率的三角形网格(见图1),近岸的最小网格步长为1 km,在外海靠近开边界处的最大网格步长为50 km,垂向平均分为10个σ层,可以对近海海域复杂多变的海底地形进行较好的拟合。模型水深值采用分辨率为1′×1′的ETOPO1的地形数据内插到计算海域的网格节点上,并利用中国航海保证部编制的海图资料对近岸水深进行补充和订正(见图2)。

图1 计算区域的网格分布图

图2 计算区域的地形和水深分布图(单位:m)

图3 东中国海沿岸验潮站和测流点分布图
岸边界取法向流速为零;在开边界处采用分辨率为 2′×2′的 YS 模型和 OHS 模型(Tidel Model Driver)提供的 M2、S2、N2、K2、K1、O1、P1、Q1八个分潮预报的水位作为开边界的强迫条件。另外,本文参考了前人的工作经验结果[8-11],并通过多次数值试验,得到适合本模型的底摩擦系数,取值为0.0025。初始条件采用零初始条件(水位值和流速值都为零),在正压模型的计算过程中,不考虑温度、盐度随时间和空间的变化,取温度为18°,盐度为35。
2.2 潮流模拟结果与实测数据对比
通过与沿岸23个验潮站(见图3)的实测资料对比,M2、S2、K1、O1四个主要分潮振幅的绝对平均误差为3.69 cm、2.67 cm、1.84 cm和1.50 cm,迟角的绝对平均误差为6.11°、6.46°、7.44°和5.35°,振幅的相关系数为0.9951、0.9755、0.9142、0.9191,迟角的相关系数为0.9355、0.9956、0.9895、0.9937,表明模拟结果与验潮站实测值符合较好,基本上正确的反映了计算海域的潮汐特征。图4为23个测流点表中底层M2和K1分潮流纬向分量(U分量)和经向分量(V分量)的振幅与迟角相关系数分布图,也可以看出模拟值与实测值符合较好。
3 潮流垂向结构分析
3.1 数值模拟结果分析
本文利用的海流资料观测点(122°35.998′E,26°30.052′N)位于东海东南部大陆架边缘海区,根据实测资料的位置在其附近海域选取了122.6ºE的经向断面和26.5°N的纬向断面,对两个断面上的潮流垂向结构进行分析和讨论,其中,前者纬度范围为26°—27°N,后者经度范围为122°—123°E,间隔为0.05°。
3.1.1 经向断面潮流特征分析

图4 M2、K1分潮流纬向分量、经向分量振幅(单位:cm/s)与迟角(单位:°)的相关性(红线表示相关系数;*表示表中底层测流点)
对潮流的模拟结果进行调和分析,得到了M2、K1分潮流的潮流椭圆要素(椭圆的长轴,短轴、倾角和格林威治位相)。图5和图6两个分潮流经向断面的潮流椭圆分布图。可以看出,M2分潮流的流速最大值达到了50 cm/s,远大于K1分潮流的流速,全日分潮流最大流速之和与半日分潮流最大流速的比值小于0.5,表明该海区为正规半日潮流区;在经向断面上,各分潮的潮流椭圆从表层到底层都为顺时针方向旋转(红色椭圆代表顺时针方向旋转,蓝色椭圆代表逆时针方向旋转,下同);表层的流速大于底层的流速,趋向海底时潮流的最大流速逐渐减小;随着深度的增加,潮流的椭圆率逐渐增大,低纬度的椭圆率小于高纬度。
在经向断面上每0.5°选取一个流速值绘制了M2和K1分潮流最大流速和最大流速流向的垂向分布(见图7)。从图中可看出,在经向断面上,随着深度的增加,M2分潮流各层的最大流速值为先增大后减小的趋势,且随着纬度的增大,最大流速值逐渐减小;从表层至底层,最大流速的极值点基本上出现在40—50 m水深处,如纬度增大,极值点出现的深度会逐步增加。M2分潮流最大流速的流向在垂向上为先右旋后左旋的趋势,该流向从低纬度至高纬度呈右旋趋势;流向的极值点分布在10—40 m水深区间,极值点出现的深度随纬度增大会逐步减小。K1分潮流最大流速值在断面的垂向分布是逐渐递减的,低纬度海区的最大流速值高于高纬度海区。随着深度的增加,K1分潮流最大流速的流向则是先右旋后左旋,流向随纬度的增大发生右旋,其极值点基本都出现在40 m左右水深处。
3.1.2 纬向断面潮流特征分析
图8和图9分别为M2和K1分潮流纬向断面的潮流椭圆分布图。从图中可以看出,在纬向断面上K1分潮流的潮流椭圆从都为顺时针方向旋转,M2分潮流大部分为顺时针方向旋转,但潮流椭圆从122.0°—122.30°E都出现了逆时针旋转的情况,即靠近岸边一侧半日分潮为逆时针旋转,随着经度的增加逐渐转变为顺时针旋转;表层的流速大于底层的流速,趋向海底时潮流的最大流速逐渐减小;从底层至表层,椭圆率逐渐减小,但经度增大椭圆率反而减小。

图5 M2分潮流经向断面潮流椭圆分布图

图6 K1分潮流经向断面潮流椭圆分布图
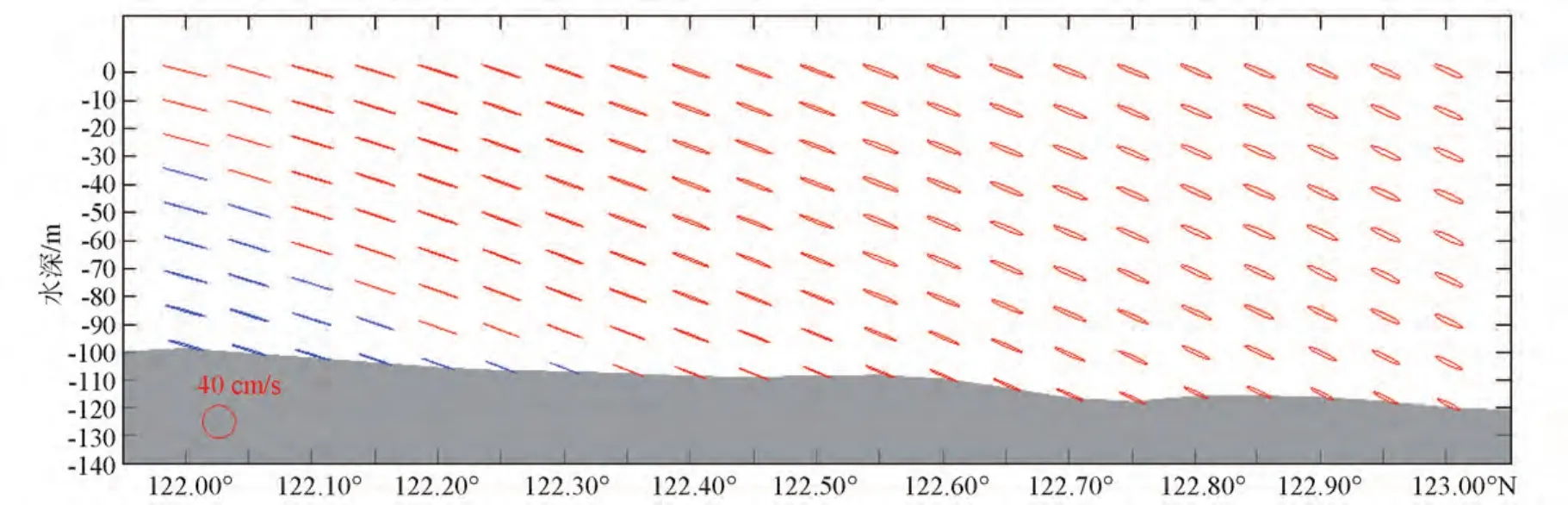
图8 M2分潮流纬向断面潮流椭圆分布图
图10为纬向断面M2和K1分潮流最大流速和最大流速流向的垂向分布图。随着深度的增加,M2分潮流各层的最大流速值为先增大后减小的趋势,且随着经度的增大,最大流速值逐渐减小;从表层至底层,最大流速的极值点基本上出现在50—75 m水深处,如经度增大,极值点出现的深度会逐步增加。M2分潮流最大流速的流向在垂向上是先右旋后左旋的趋势,该流向从低经度至高经度呈左旋趋势;流向的极值点基本都出现在27 m左右水深处。K1分潮流最大流速值在断面的垂向分布是逐渐递减的,但随着经度的增大各层最大流速的变化很小,基本在3—5 cm/s之间。随着深度的增加,K1分潮流最大流速的流向则是先右旋后左旋,流向随经度的增加发生左旋,极值点分布在30—75 m水深区间,极值点出现的深度随经度增大会逐步增加。

图9 K1分潮流纬向断面潮流椭圆

图10 纬向断面M2和K1分潮流最大流速及流向垂向分布
3.2 实测海流资料分析
海流资料观测点处水深约为113 m,垂向空间分辨率为8 m,共取13层,但实际连续并可供分析的资料只有11层,测量水深的范围为24—104 m。有效观测时间是从2008年9月20日6时—2009年4月6日7时,数据采样时间间隔为10 min。
对实测海流数据进行调和分析,得到了每个观测层的M2和K1分潮流椭圆要素。根据各观测层的潮流椭圆要素的分布绘制出了分潮的潮流椭圆的垂向分布图(见图11),其中红色椭圆代表顺时针方向旋转,蓝色椭圆代表逆时针方向旋转。可以看出每一层潮流的最大流速都是M2分潮流远远大于K1分潮流。各观测层上全日分潮流最大流速之和与半日分潮流最大流速的比值都小于0.5,即每一层都是半日分潮占优,潮流为正规半日潮流,与前面分析的结果保持了一致。M2分潮流各观测层短轴皆为负值,表明该观测点半日分潮流主要呈顺时针方向旋转。K1分潮流在80 m层以上是顺时针方向旋转,80 m层以下是逆时针方向旋转。

图11 M2和K1分潮潮流椭圆垂向分布
图12给出了M2和K1分潮流最大流速随深度的变化情况,可以看出在垂向上M2分潮流的最大流速总的变化趋势都是随着深度的增加先增大后减小,但在变化的过程中会发生小幅度的震荡。M2分潮流在各个观测层内都比较显著,最大流速变化比较小,从上层至下层都在40 cm/s左右变动,最大值出现在88 m层为41.09 cm/s,然后逐渐减小至104 m层最小值33.85 cm/s。K1分潮流垂向分布趋势为逐渐减小,最大流速在32 m层达到最大值6.05 cm/s,之后随着深度逐渐递减,至104 m处减小为2.37 cm/s。
M2和K1分潮最大流速流向的垂向分布如图13所示,M2分潮流的最大流速方向在24 m层至32 m层先小量的右旋,达到最大值140.20°,然后在140°附近发生小幅度的震荡(32 m层至64 m层),最后逐渐左旋至104 m层的135.20°,即该分潮流的最大流速流向随着深度的增加先右旋(顺时针),经过微小震荡后在64 m层以下改为左旋(逆时针)。K1分潮的最大流速流向先左旋,从32 m层至56 m层右旋至最大的140.25°,之后随深度的增加大幅度左旋至104 m层的91.82°。
3.3 潮流垂向结构实测值与模拟值对比分析

图12 M2和K1分潮流最大流速垂向分布

图13 M2和K1分潮流最大流速的流向垂向分布
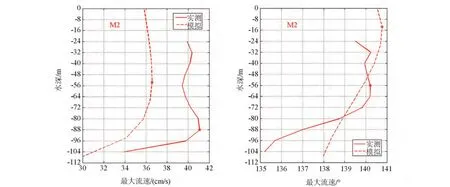
图14 M2分潮流最大流速及其流向垂向分布对比
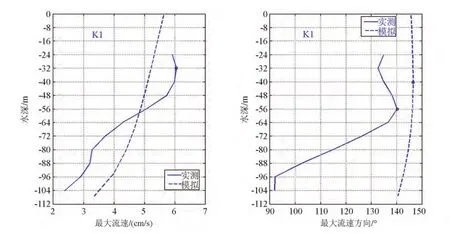
图15 K1分潮流最大流速及其流向垂向分布对比
在断面上选取122.6°E,26.5°N处的M2和K1分潮流的垂向结构与实测点进行对比分析,图14和图15分别为M2和K1分潮流最大流速及最大流速流向的垂向分布。从图中可知,随着深度的增加,M2分潮流最大流速的模拟结果和实测结果的垂向变化趋势比较相似,同为先增大后减小,前者的流速值要稍小于后者,模拟结果最大流速的极值点大约在水深55 m左右,而实测结果出现在88 m处。M2分潮流最大流速的流向在垂向上都为先右旋后左旋的趋势,各层的流向差别不大,模拟的极值点大约在15 m左右,深度15 m以下流向保持了左旋的趋势,而实测资料的流向在56 m层以上右旋,以下左旋。
模拟和实测的K1分潮流最大流速的变化趋势都为随深度的增加递减,两者的流速值比较接近。该分潮流最大流速的流向从表层至底层基本上都是先右旋后左旋,极值点比较接近分别出现在40 m和56 m,但实测结果在56 m层以下最大流速方向变化剧烈,从140°快速左旋至90°左右,与模拟结果的差别较大。
通过潮流的模拟结果与实测结果的对比分析,该海域半日分潮流最大流速随深度的增加先增大后减小,最大流速流向在极值点的上层右旋,在下层左旋;全日分潮流的最大流速在垂向上呈递减趋势,其流向同样是在上层右旋,在下层左旋。表明了模拟结果与实测结果关于潮流垂向结构的总体趋势是比较一致的,但最大流速及其流向的大小略有不同,且极值点出现的深度也有差别,主要原因可能是该海区处于黑潮流经海域附近,实测资料受到黑潮的影响比较大,导致模拟结果与实测结果存在一定的差异。另外,该海域水深较浅,多变的海底地形也应该是两个结果存在差异的影响因素。
4 结论
通过潮流的模拟结果与实测结果的对比分析,研究了海流观测点附近海域的潮流垂向结构,可以得出以下结论:
(1)潮流椭圆基本上为顺时针方向旋转,但靠近岸线处的半日潮流椭圆为逆时针方向旋转;椭圆率随深度的增加逐渐增大,低纬度的椭圆率小于高纬度,但经度增大椭圆率会减小;
(2)半日分潮流的最大流速值随纬度的增加逐渐减小,且极值点出现的深度值增大;最大流速的流向从低纬度至高纬度呈右旋趋势,极值点出现的深度随纬度增大会逐步减小。低纬度海区的全日分潮流最大流速值高于高纬度海区;最大流速的流向随纬度的增大发生右旋,极值点的深度变化不大;
(3)半日分潮流各层的最大流速值随着经度的增大逐渐减小,且极值点出现的深度随经度增大会逐步增加;最大流速的流向随经度增加呈左旋趋势,极值点的深度基本相同。全日分潮流随着经度的增大各层最大流速的变化很小;最大流速的流向随经度的增加发生左旋,极值点出现的深度随经度增大会逐步增加;
(4)该海域半日分潮流最大流速随深度的增加先增大后减小,最大流速流向在极值点深度的上层右旋,在下层左旋;全日分潮流的最大流速在垂向上呈递减趋势,其流向同样是在极值点深度的上层右旋,在下层左旋。
[1]Guo X Y,Yanagi T.Three-dimensional structure of Tidal current in the East China Sea and the Yellow Sea[J].Journal of Oceanography,1998,54(6):651-668.
[2]王凯,方国洪,冯士笮.渤海、黄海、东海M2潮汐潮流的三维数值模拟[J].海洋学报,1999,21(4):1-13.
[3]Lee J C,Jung K T.Application of eddy viscosity closure models for the M2tide and tidal currents in the Yellow Sea and the East China Sea[J].Continental Shelf Research,1999,19(4):445-475.
[4]Bao X W,Gao G P,Yan J.Three dimensional simulation of tide and tidal current characteristics in the East China Sea[J].Oceanologica Acta,2001,24(2):135-149.
[5]方国洪.潮流垂直结构的基本特征— —理论和观测的比较[J].海洋科学,1984,(3):1-11.
[6]叶安乐.分潮流最大流速发生时刻随深度变化的特征[J].海洋通报,1984,3(2):1-8.
[7]Chen C S,Liu H D,Beardsley R C.An unstructured grid,finite-volume,three-dimensional,primitive equations ocean model:Application to coastalocean and estuaries[J].Journal of Atmospheric and Oceanic Technology,2003,20(1):159-186.
[8]李培良.渤黄东海潮波同化数值模拟和潮能耗散的研究[D].青岛:中国海洋大学,2002.
[9]李磊.渤黄东海潮波系统的有限元模拟[D].青岛:中国海洋大学,2003.
[10]林俊.风暴作用下的近岸悬浮泥沙数值模拟[D].青岛:中国海洋大学,2007.
[11]朱学明.中国近海潮汐潮流的数值模拟与研究[D].青岛:中国海洋大学,2009.
