基于MATLAB的机床液体静压导轨油膜厚度控制系统研究

张振东王 菲胡 建

（1 安徽工程大学机电学院，安徽 芜湖 241000）

（2 安徽工程大学机械与汽车学院，安徽 芜湖 241000）

（3 哈特机器人研究院，安徽 芜湖 241000）

基于MATLAB的机床液体静压导轨油膜厚度控制系统研究

张振东1王 菲2胡 建3

（1 安徽工程大学机电学院，安徽 芜湖 241000）

（2 安徽工程大学机械与汽车学院，安徽 芜湖 241000）

（3 哈特机器人研究院，安徽 芜湖 241000）

设计了液体静压导轨油膜厚度的控制系统，据此进行了普通PID控制器和模糊PID控制器仿真分析，结果表明，模糊PID控制器的动态响应性能和控制精度比普通PID控制器更好，更能满足机床开式液体静压导轨油膜厚度控制的要求。

开式导轨；油膜厚度；PID控制；模糊控制；MATLAB

引言

本文通过对导轨—油液数学模型的建立运用MATLAB分析导轨油膜控制的稳定性，设计出普通PID控制器和模糊PID控制器并分别进行了仿真分析，提出了由变频器、电动机、变量泵构成的液体静压导轨改进型供油系统，推导了其数学模型［1］。该系统使用变频器控制异步电动机转速，电动机转速的改变带动变量泵的流量发生改变，使得导轨的油膜厚度随之改变，直至趋于恒定值。其工作原理如图1：

图1中：1—变频器，2—变量泵，3—过滤器，4—进油口，5—动导轨，6—油箱，7—过滤器，8—节流阀，9—溢流阀。

图1 静压导轨油膜厚度控制系统原理图

变量泵将已过滤的油液经节流阀输送到导轨油腔中，油压和中心油腔产生的压力场共同组成承载压力，用来平衡外负载力。当导轨油腔中的压力足以平衡外负载力时，上支撑导轨被浮起，此时油液经过上、下支承的间隙流出，压力降为零。当浮起量大于支承上、下两个平面的表面粗糙度时，即形成纯液体摩擦。如果上支撑表面的外负载W增大时，那么上支撑则会出现下沉的趋势，油膜被压缩，导致导轨面之间的油液外流的液阻增加。节流阀具有调压的作用，使油腔压力增加，平衡外界负载。最终实现油膜厚度的控制。

机床静压导轨油膜厚度控制系统主要由计算机、D/A、变频器、电机、泵、导轨和传感器等。静压导轨油膜厚度控制框图如图2所示，理想油膜厚度h和位移传感器测量的实际油膜厚度h1相比较形成误差△h，对△h经过计算器进行控制算法计算，D/A把数字量信号转化成变频器可以接受的模拟信号，控制变频器的频率，变频器可以改变电机的转速从而改变泵的转速，使泵输出的油液流量跟随油膜厚度的变化而变化。本文主要从导轨油膜厚度控制系统和流量控制系统研究油膜厚度。

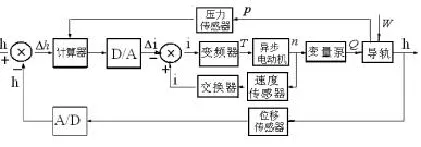
图2 静压导轨油膜厚度控制系统框图

1 导轨—油液数学模型的建立

油膜厚度控制系统模型包括被控对象泵-导轨模型和导轨—油液控制模型两部分，其核心是导轨—油液控制模型。

1.1 导轨—油液耦合模型

导轨—油液的数学模型主要由导轨流量方程和导轨受力方程组成。导轨流量主要由体积压缩导致的填充流量和间隙流量组成，导轨流量方程是在缝隙流动的原理上建立的，其流量方程如式（1）所示：

式中：q—进入导轨的流量；

v1—油液体积（mm3）；

βe—油液体积弹性模量（k/MPa）；

b—导轨宽度（mm）；

h—油膜厚度（μm）；

μ—动力粘度（Pa·s）；

l—导轨长度（mm）；

p—导轨间隙压力。

将流量方程在理想油膜厚度h0处利用泰勒公式展开并进行拉氏变换可得式（2）：

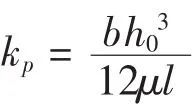
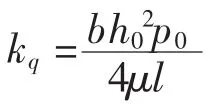
在此控制系统中动导轨主要受自身重力、切削力、油液对动导轨的摩擦力和液体对导轨的作用总力。在分析动导轨的受力方程时，不妨假设油腔缝隙流动为层流，液体对导轨的压力是线性分布，则其受力方程为：

式中：m—动导轨质量；

c—油液阻尼系数；

k—比例系数；

A—导轨与油液接触面积；

Fg—重力及切削力。

对式（3）进行拉氏变换并代入（2）式，可得：

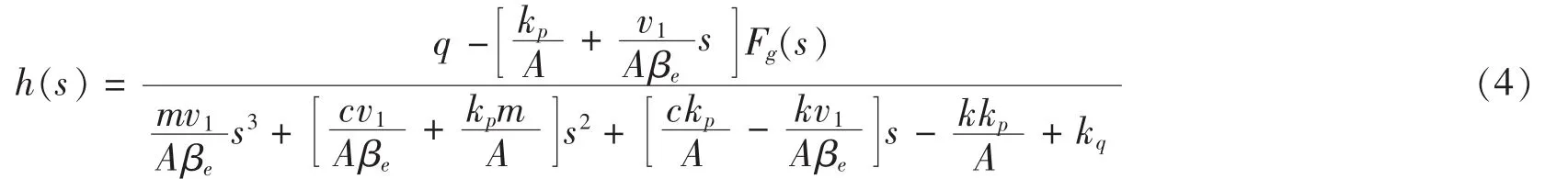
通过实验优化，式（4）中相关参数值如表1所示［2］：

表1 静压导轨油膜控制系统参数值

表1中的相关参数带入式（4）中，经化简可得导轨—油液的数学模型：

式（5）是静压导轨油膜控制系统导轨—油液的数学模型，建立此数学模型，需要对该数学模型的稳定性和控制系统的性能进行进一步的分析研究。

1.2 静压导轨油膜控制系统稳定性分析

静压导轨油膜控制系统稳定性的判断方法有很多种，例如：李雅普诺夫定理、根轨迹法、解析法、Nyquist图和bode图的方法等。本文主要采用根轨迹法、Nyquist图法分析该控制系统的稳定性，根轨迹法表明如果数学模型中所有特征根落在S的左半平面，则此控制系统稳定。Nyquist法表明如果数学模型Nyquist曲线不包围（-1，j0）点，则此控制系统稳定。

根据MATLAB编程的相关知识，得到静压导轨油膜控制系统模型的零极点图和Nyquist图如下：

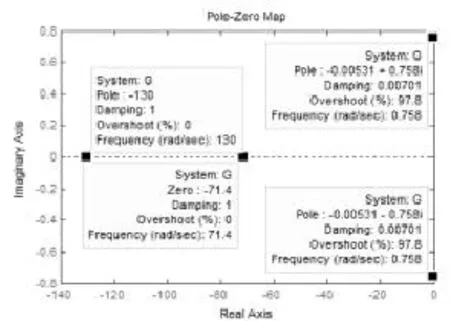
图3 零极点图

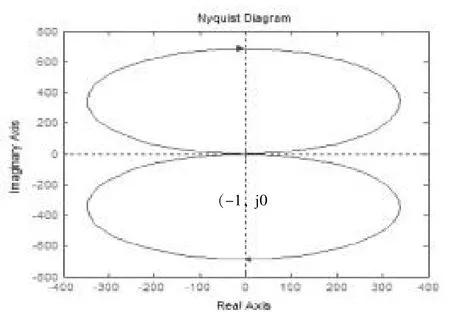
图4Nyquist图

由图3可知静压导轨油膜控制系统特征方程的根全部落在了S的左半平面，该系统稳定，但是由于该系统特征方程的共轭复根-0.00531±0.758i的实部接近于零，且由图4知，（-1，j0）点在Nyquist曲线上，故系统稳定性偏差。

1.3 静压导轨油膜控制系统PID仿真

由于上述静压导轨油膜控制系统的模型稳定性较差，为改善其稳定性，需对该系统增加控制器，本文选用PID控制器，PID控制器中比例环节起着减少控制系统的偏差的作用，积分环节有消除控制系统的静态误差，提高其无差度的作用；微分环节主要是提高控制系统的动态性能。

在系统加入PID控制前后，利用MATLAB中的simulink对系统进行仿真，其模型图5所示：

图5 加入PID前后静压导轨油膜控制系统导轨—油液的数学模型

按照PID中三个参数的调节规律，对各个系数进行不断的调整，得出最佳的三个参数值分别是，kp=-160 ki=-8 kd=-9.6。经过simulink仿真，可得图6所示的加入PID前后静压导轨油膜控制系统的单位阶跃响应图：

图6 加入PID静压导轨油膜控制系统单位阶跃响应图

由图6可知：加入PID后静压导轨油膜厚度控制系统的超调量，得到很大改善，当输入单位阶跃信号时，静压导轨油膜控制系统的输出能达到理想的输出信号要求，与输入信号基本吻合，输出信号稍有波动，由此可得，加入PID控制后使静压导轨油膜控制系统的性能得到一定的提高。

2 静压导轨流量控制模型建立

对静压导轨流量控制系统的研究主要是指对变频器、电机和泵的控制系统的研究。图7是静压导轨流量控制系统框图

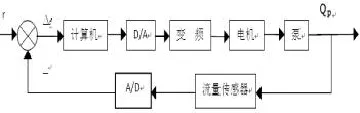
图7 静压导轨流量控制系框图

由图7可知：输入信号r与经过模数（A/D）转换后的数字量之差为Δe，数字量Δe经计算机的优化，经过数模（D/A）转换器将数字信号转化成模拟信号，此模拟信号能使变频器频率发生改变，从而引起电机的转速发生变化，带动泵的转速发生变化，达到改变泵的流量Qp的目的。

下面建立静压导轨流量控制系统的数学模型，静压导轨流量控制系统的数学模型就是变频器、电机和泵的数学模型的有机结合。

2.1 静压导轨流量控制变频器的数学模型

由变频器的相关知识可知，在不考虑低频工作时转矩的补偿电压的情况下，电源频率f1和电机的相电压u1的表达式为［3］：

式中：uc—变频器输入电压（v）；

kint—电压频率系数（Hz/v），由于uc为0-10v，f1为0-50Hz，则取kint为5Hz/v；

kf—转换系数，kf=4.4v/Hz。

将式（6）经过拉氏变换可得变频器的数学模型为：

2.2 静压导轨流量控制电机的数学模型

根据电机的知识可知，电机可以简化为三个环节，两个惯性环节和一个延时环节，经过实验可知电机简化的传递函数为［4］：

式中：K—为系统增益常数

T1—惯性常数

T2—惯性常数

τ—为滞后时间常数

由相关资料和实验可知K=1，T1=32.8s，T2=0.2s

可得电机控制模型为：

2.3 静压导轨流量控制泵的数学模型

根据泵的知识可知，恒压变量泵的流量与转速成正比，有：

式中：Q1—泵的额定流量（m3/s），；

Q2—泵的实际输出量（m3/s）；

n1—电机的额定转速（r/s）；

n2—电机的实际转速（r/s）。

ka为定值，令ka等于1

对式（10）进行拉氏变换可得泵的数学模型：

故此静压导轨流量控制系统数学模型为：

2.4 静压导轨流量控制系统稳定分析

控制系统稳定性的分析方法多种多样，本文采用解析法对静压导轨流量控制系统稳定进行分析，令s=jω，带入式（12）可得静压导轨流量控制系统的频率特性为：

则静压导轨流量控制系统总的对数幅频特性为：

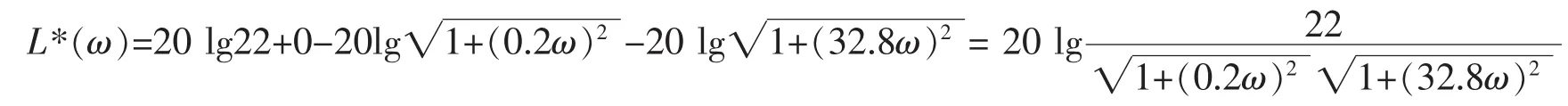
静压导轨流量控制系统总的对数相频特性为：

式中：ωc—剪切频率；

ωg—相角穿越频率。

由式（14）解得：ωc=0.6642，ωg=0.9441

经过剪切频率ωc和相角穿越频率ωg可以求出相角裕度γ和幅值裕度Kg（dB）分别为：

由上述可知，静压导轨流量控制系统的相角裕度和幅值裕度都大于0，故此控制系统稳定。

2.5 静压导轨流量控制系统PID仿真

为了研究静压导轨流量控制系统需对其控制模型进行简化，将简化后所得的静压导轨流量控制系统与加入PID控制后的静压导轨泵流量控制系统进行比较，比较模型如图8所示：

图8 加入PID前后静压导轨泵流量系统框图

利用MATLAB中的simulink对系统进行仿真，其运行结果如图9。

由图9可知：未加PID前系统稳定时间在40s左右，加入PID后系统在15s内达到稳定。由此可知，加入PID控制后静压导轨流量控制系统的性能很大改善。

2.6 静压导轨流量控制系统模糊PID仿真

由于PID校正存在一定的局限性且PID参数需人为校正，十分费时，如果调试者缺乏经验很难整合出合理的参数［1］，即使能调出合理的参数，随着环境和系统运行时间的推移，PID参数也需重新调整。由此本文引入模糊PID控制理论。

模糊PID控制结合了普通PID控制和模糊控制的优点。图10是静压导轨泵流量控制系统的模糊PID控制器结构图，由图10可知，偏差E和偏差变化率EC是模糊PID控制器的输入量，Kp、Ki、Kd是模糊PID控制器的输出量，它可以在线调节出PID最佳的三个控制参数，从而提高静压导轨泵流量控制系统的性能［5-7］

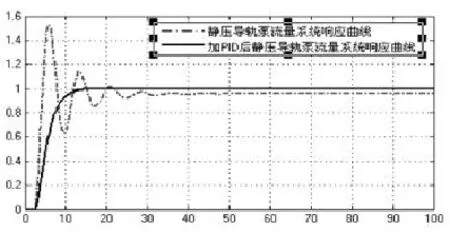
图9 加入PID前后静压导轨泵流量控制响应曲线

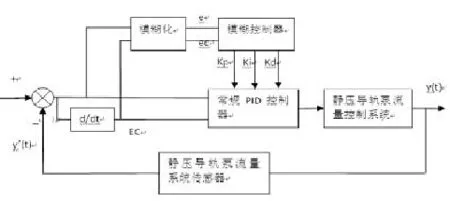
图10 静压导轨泵流量控制系统的模糊PID控制器结构

由图10可知：PID的三个控制参数由偏差e和偏差变化率ec决定。在本文中，输入变量以及输出变量的语言值可以分为7个语言值，即NB、NM、NS、0、PS、PM、PB，也就是负大、负中、负小、0、正小、正中和正大［8］。模糊PID控制器对PID中的三个参数进行在线整定，可以求解出最佳的三个控制参数。偏差e和偏差变化率ec的论域取｛-3～3｝，输出量Kp的论域取｛-0.3～0.3｝，Ki的论域取｛-0.06～0.06｝，Kd的论域取｛-3～3｝，则偏差e、偏差变化率ec、输出量Kp、Ki、Kd的隶属度函数如图11至15所示：

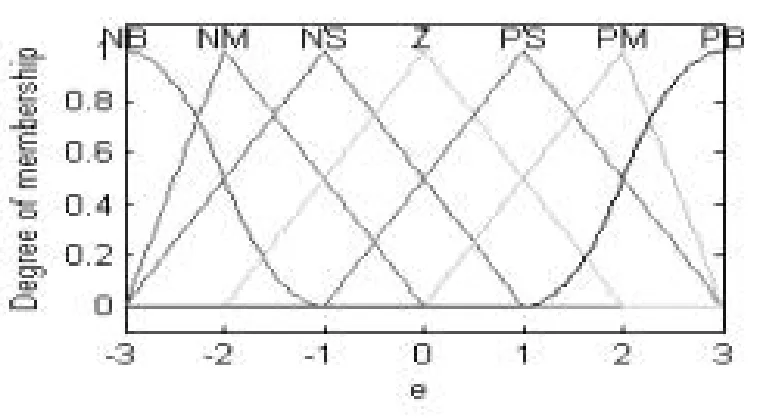
图11e隶属度函数

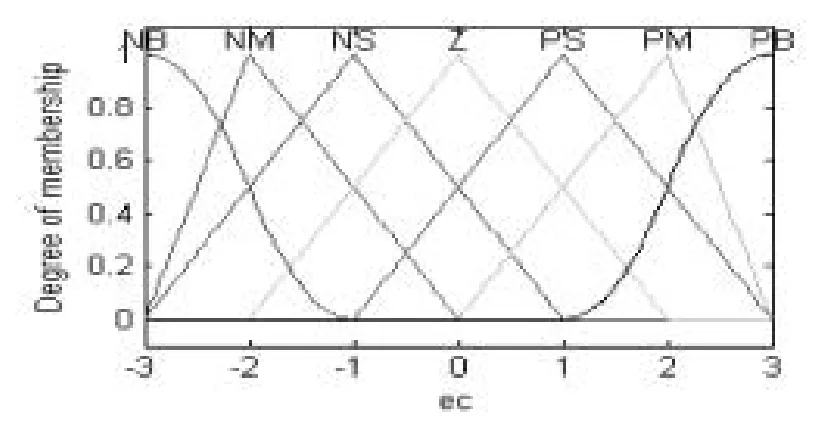
图12ec隶属度函数

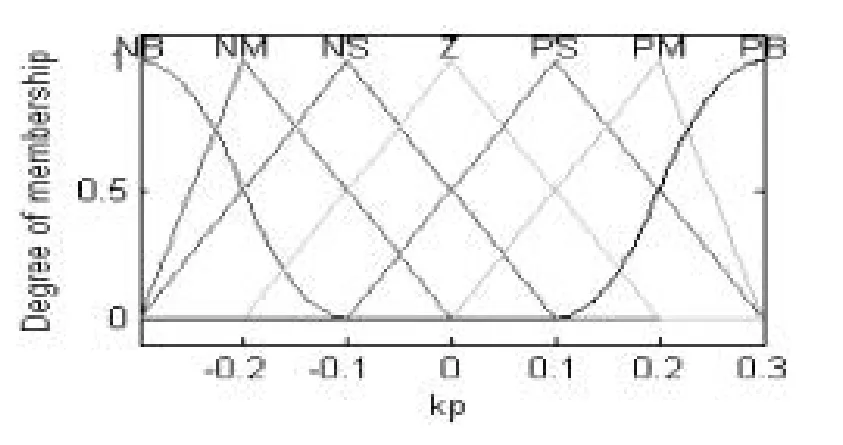
图13Kp隶属度函数

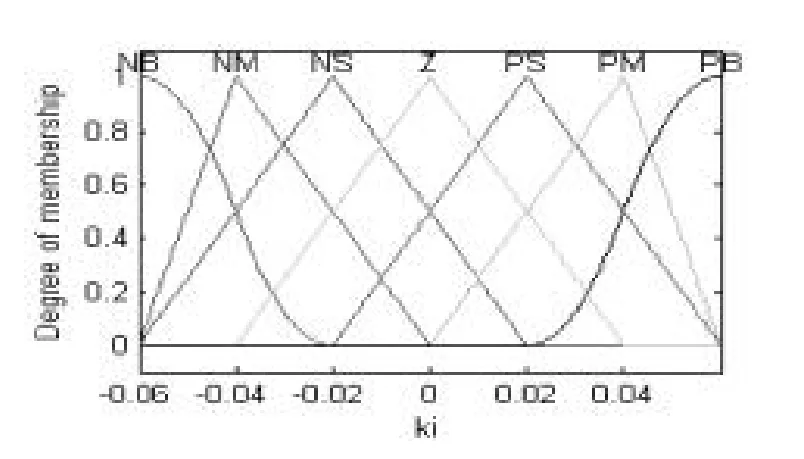
图14Ki隶属度函数

图15 Kd隶属度函数

模糊PID控制的核心是建立合适的模糊控制规则表，PID中的Kp、Ki、Kd三个参数的规则表［9］，如表2、表3、表4所示：

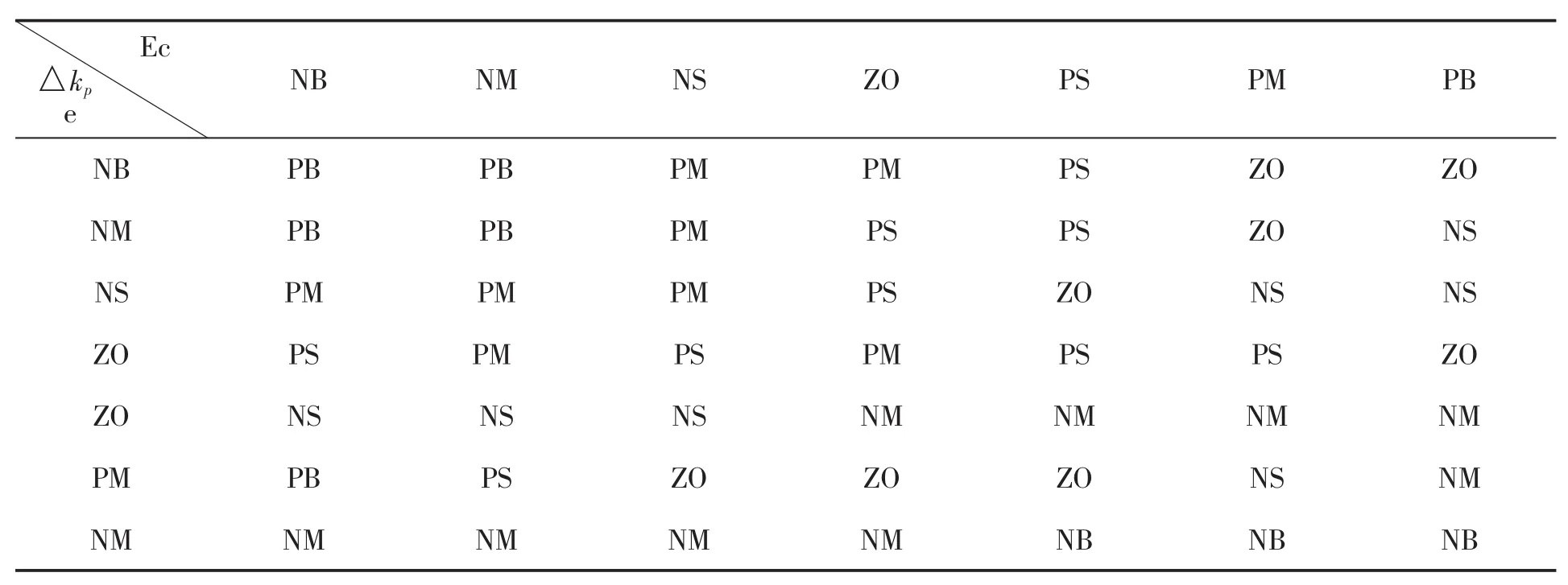
表2 Kp的模糊控制规则表

表3 Ki的模糊控制规则表

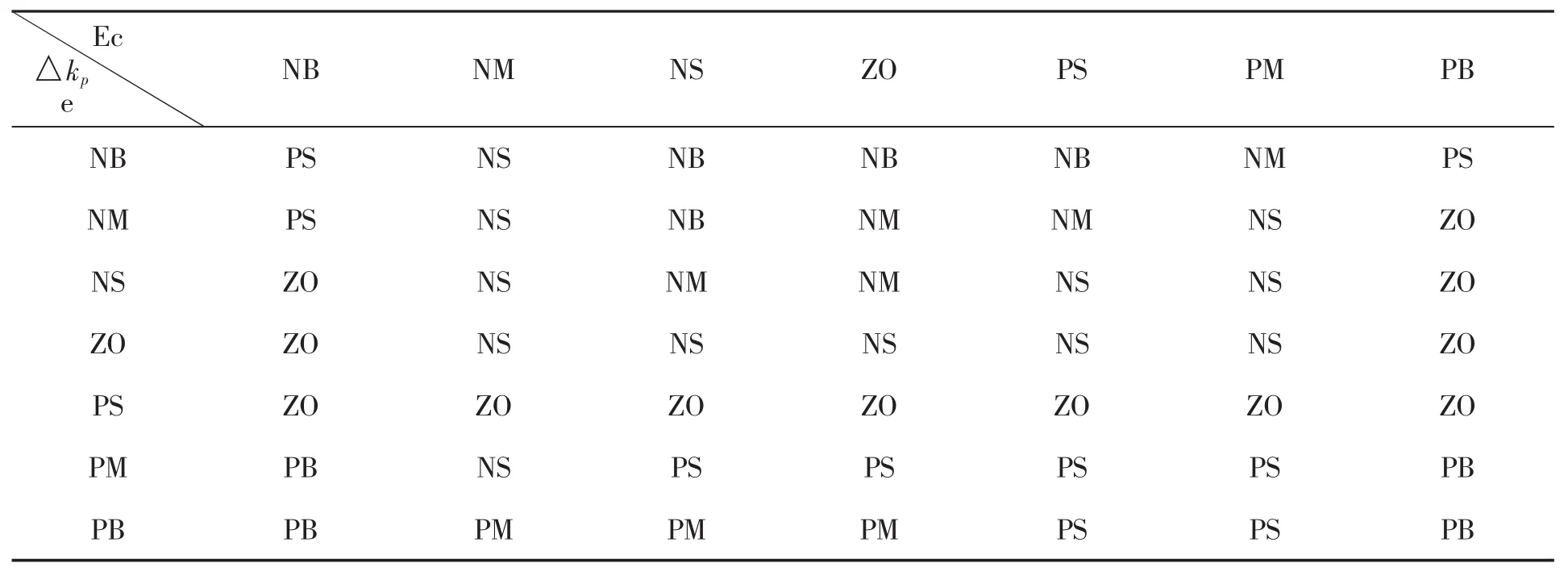
表4 Kd的模糊控制规则表

根据模糊PID控制和MATLAB编程的相关知识，对静压导轨泵流量控制系统进行编程仿真，图16是模糊PID控制系统的阶跃响应图。

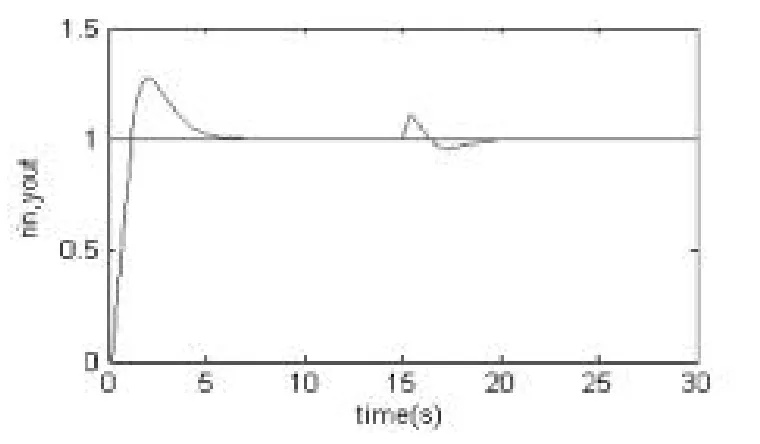
图16 模糊PID控制系统的阶跃响应图

图17 模糊PID控制系统的误差图

由图16可知：静压导轨泵流量给定值为1，在7.5s时静压导轨泵流量控制系统达到稳定，与普通PID控制的静压导轨泵流量控制系统相比，模糊PID控制达到稳定所需要的时间很少。在15s给静压导轨泵流量控制系统加入干扰信号，在20s时此控制系统达到理想的稳定状态，由此可知：模糊PID控制具有很强的抗干扰能力，它不仅提高了静压导轨泵流量控制系统的性能，同时也说明了模糊PID控制方法比普通PID控制方法更加优越。

图17为模糊PID控制系统的误差图，由图17可知：在6s左右静压导轨泵流量控制系统的误差减小为0，在15s时给该控制系统加入干扰信号，在20s左右误差再次减小为0，同样证明了模糊PID控制具有抵抗外界干扰的能力。

模糊PID控制对PID的三个控制参数进行在线整定，可以得到最佳的Kp、Ki、Kd的控制参数，图18至图20是PID的三个控制参数仿真结果图。

图18 模糊PID控制的Kp系数在线整定图

图19 模糊PID控制的Ki系数在线整定图

图20 模糊PID控制的Kd系数在线整定图

由图18至图20可知：模糊PID控制的3个参数经过在线整定均在5S内达到稳定。较之普通PID控制有了很好的改善，工作效率明显提高。

3 结论

本文通过对导轨—油液控制系统和流量控制系统模型的建立，使用根轨迹和Nyquist图的方法分析静压导轨油膜控制系统的稳定性并对其控制系统进行PID优化设计和Simulink仿真，使导轨—油液控制系统达到稳定，在流量控制系统模型的建立中，分别对变频器、电机和泵进行了模型建立，得出流量控制系统模型，使用解析法分析其稳定性，对其系统进行普通PID和模糊PID优化设计，使系统稳定性进一步提升。导轨—油液控制系统和流量控制系统模型的建立能够使变量泵输出的油液流量稳定的随油膜厚度变化而变化，改变动、支撑导轨间流体压力，从而使导轨油膜厚度稳定。

［1］张晓彤.开式静压导轨油膜厚度控制方案研究［D］.哈尔滨：哈尔滨理工大学，2007.

［2］乔金宇.基于MATLAB/SIMULINK的锅炉汽包水位控制策略及仿真分析［D］.兰州：兰州理工大学，2013.

［3］彭天好.变频泵控马达调速及补偿特性的研究［D］.杭州：浙江大学，2003.

［4］XueSong Zhao，Jian Hu，PeiCheng Shi.Hydromechanics Research of Pump Flow Control System Based on BP Neural Network PID［J］.Applied Mechanics and Materials，2013，（327）：222-226.

［5］V.Mukherjee.，S.P.Ghoshal..Inte1ligent particle swarm optimized fuzzy PID controller for AVR system［J］.Electric Power SystemsReseareh，2007，（12）：1689-1698.

［6］Chen G.Conventional and Fuzzy PID Contrpllers.An overview［J］.Int.J.of Intelligent Control Systems，1996，（1）：235-246.

［7］董春宵，赵元黎，张永利，等.Fuzzy-PID算法在气体流量控制中的应用［J］.微计算机信息，2008，（25）：31-33.

［8］王恒.球磨机负荷加权模糊控制算法设计与仿真［J］.电力自动化议备，2009，（2）：117-120.

［9］鲁俊，胡建.湿法烟气脱硫中PH值模糊PID控制［J］.新乡学院学报（自然科学版），2013，（5）：364-367，372.

RESEARCH ON THE CONTROL SYSTEM OF OIL FILM THICKNESS FOR LATHE HYDROSTATIC RAIL BASED ON MATLAB

ZHANG Zhen-dong1WANG Fei2HU Jian3
（1 Anhui Polytechnic University，Mechanical&Electrical College，Wuhu Anhui 241000）
（2 Anhui Polytechnic University，Wuhu Anhui 241000）
（3 Wuhu HIT Robot Technology Research Institute Co.，Ltd.，Wuhu Anhui 241000）

This paper is aimed at designing the control system of oil film thickness for the hydrostatic rail. General PID controller and fuzzy PID controller are simulated and analyzed，and the results shows that the fuzzy PID controller has better dynamic performance and higher precision than general PID controller， and it can meet the requirements of the oil film thickness control for open lathe hydrostatic rails.

open rails；oil film thickness；general PID controller；fuzzy controller；MATLAB

陈小举

TH11

A

1672-2868（2015）03-0068-10

2015-01-11

张振东（1985-）男，安徽阜阳人。安徽工程大学，助教，硕士。研究方向：机械设计制造及其自动化。