一种超音速火箭靶弹程序角优化方法研究

沈冠军, 冯顺山, 曹红松

(1.中北大学 机电工程学院， 山西 太原 030051; 2.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)



一种超音速火箭靶弹程序角优化方法研究

沈冠军1, 冯顺山2, 曹红松1

(1.中北大学 机电工程学院， 山西 太原 030051; 2.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

针对方案制导超音速火箭靶弹平飞段供靶性能优化问题，提出了一种俯仰程序角优化方法。考虑靶弹弹道始末端点约束及平飞段性能约束，在火箭靶弹纵向飞行平面内建立起俯仰程序角优化设计模型。基于Gauss伪谱法将飞行过程约束转化成对俯仰程序角的约束，将最优控制问题转换为对俯仰程序角的非线性规划问题；利用序列二次规划算法求解。仿真结果表明，该方法能够快速获取最优俯仰程序角，并且具有良好的鲁棒性，为实际工程设计提供参考。

兵器科学与技术； 超音速靶弹； 平飞弹道； 程序角优化； Gauss伪谱法

0　引言

超音速靶弹是用于防空武器试验鉴定及日常训练时的模拟靶标，常见的研制方式有：利用现役和退役的火箭或导弹改装；根据供靶指标专门研制新型靶弹。因成本等因素限制，通过对无控火箭弹加装简易控制装置，设计合理的控制程序，使得简易控制火箭弹能够模拟飞机、巡航导弹等目标所具有的平飞和俯冲弹道特性，这种设计方式得到了大量应用。文献[1]提出一种对无控靶弹预置平衡攻角产生升力抵消靶弹重力，并通过陀螺舵等措施防止靶弹旋转形成平飞来模拟巡航导弹的平飞特性。文献[2]提出一种对大射程火箭弹改进实现供靶的简易控制火箭靶弹总体设计方案，通过设计程序俯仰角，在被动段实现有攻角飞行进而实现平飞弹道。

实现平飞或俯冲等弹道特性实质上是对控制变量最优解的求解过程。近年来，运用最优控制理论求解弹道优化问题越来越广泛。文献[3]应用极大值原理求解弹道修正引信弹道优化模型，得到了最优法向控制量。文献[4]针对间接法进行弹道优化时无法获得全局最优解的缺点，提出了一种改进方法。伪谱法作为直接法的一种，通过离散控制变量和状态变量将控制问题转换成为非线性规划问题，具有设置参数较少，计算精度较高等特点，逐渐成为求解最优控制问题的热门方法。文献[5]利用Radau伪谱法将助推- 滑翔飞行器弹道优化问题转换为非线性规划问题，得到了最优规避弹道。文献[6]根据伪谱法将再入动力学微分方程约束转换成代数方程约束，将制导问题转换为不需要积分的最优规划问题。伪谱法种类多，根据配点、节点位置及插值函数的不同而不同，常见用于航空航天领域的有Radau伪谱法、Legendre伪谱法和Gauss伪谱法。Gauss伪谱法在对状态变量、控制变量和协状态变量的近似精度以及收敛速度均优于其他两种伪谱法，同时在对协状态变量边界值的估计精度和处理含有初始和终端约束的问题上具有优势[7]。本文针对超音速靶弹平飞性能优化问题，利用Gauss伪谱法对超音速火箭靶弹程序角进行优化设计，实现靶弹在供靶过程中的最优平飞特性。

1　靶弹供靶弹道方案描述

为模拟超音速飞机与导弹等目标的高空高速特性，需要靶弹能够在预定的高度稳定地平飞，以提供具备上述目标特性的供靶弹道。常见的靶弹飞行弹道形式如图1所示。

图1　供靶方案Fig.1　Scheme for target

本文所研究的火箭靶弹是在常规火箭弹的基础上加装控制机构改装而成，执行机构为两对相互垂直安装的“十字”鸭舵，采用程序控制与位置修正相结合的方式，通过对程序角的控制，实现预定形式的供靶弹道。靶弹在飞行过程中，通过在稳定尾翼上加装气动陀螺舵产生阻止靶弹横滚的阻尼力矩等方式，改善靶弹整体的横滚特性，本文假设靶弹发射后在飞行过程中不滚转。弹载GPS模块及捷联惯性测量装置获得靶弹某一时刻位置及姿态信息，弹载控制系统计算得到当前弹道与预装订的供靶方案弹道之间的偏差量，进而按照既定的控制律经稳定回路计算得出靶弹位置及姿态修正量，并发送给舵机执行，一对方向舵和俯仰舵分别进行靶弹横向和纵向的偏差修正，从而消除靶弹位置及姿态偏差，控制靶弹按既定的供靶方案弹道稳定飞行，实现平飞、俯冲等运动特性。供靶方案弹道设计的好坏，直接影响靶弹供靶性能及飞行稳定性，因此在设计供靶方案弹道时应尽可能在满足供靶指标下，设计合适的程序角优化方法，并结合优化方法收敛的有效性和快速性，以寻求最优平飞或俯冲供靶弹道。

传统的靶弹弹道设计方法是针对弹道不同阶段设置不同的俯仰角来实现的。由图1可将靶弹弹道简单分为升弧段、平飞段和俯冲段。在升弧段，靶弹按照指定的俯仰角进行爬升。当到达预定平飞高度后在程序俯仰角的作用下，火箭靶弹整体形成正向攻角以产生升力平衡弹体自身重力。由于攻角的存在，靶弹飞行速度不断减小，故需要不断改变俯仰角的大小，使得靶弹按照预定的高度进行平飞，当平飞条件结束后，靶弹按照一定的俯仰角俯冲飞行直至落地。经典的程序俯仰角设计满足如下形式：

(1)

式中：ϑ0、ϑp分别为靶弹初始俯仰角和平飞时俯仰角；t1、t2为给定指令起控的时间；Kc为控制参数。那么在已知靶弹的飞行参数时，按照经典的程序角形式需对上述5个参数进行设计组合。在诸多的组合方案中存在一组或多组最优解，寻得最优解的过程十分困难与繁杂，同时由于火箭靶弹弹道设计空间高度不连通，往往存在着多个局部最优解。以最优控制的角度来看，实现平飞弹道实质就是求解满足图1所示形式的弹道约束的控制变量最优值的求解问题。

2　靶弹动力学模型建立

本文建立的火箭靶弹动力学模型满足如下基本假设：

1)飞行过程中靶弹侧偏为0，忽略火箭靶弹横向平面运动，只在纵向飞行平面内建立运动模型；

2)弹体无滚转，整个飞行过程中火箭靶弹只受弹翼整体的阻力、升力，控制舵的阻力、升力，全弹的重力，弹翼整体的稳定力矩、控制舵产生的控制力矩，忽略其他次要力和力矩的影响；

3)控制系统是理想的，能够对连续信号实时做出响应，即无误差，无时间延滞，能随时输出要求的舵偏角。

在满足上述假设条件下，在速度系中建立火箭靶弹纵向平面内有控动力学模型：

(2)

式中:m为靶弹质量；A、v、θ、ω、x、y、φ、δ分别为火箭靶弹赤道转动惯量、速度、弹道倾角、俯仰角速度、射程、射高、俯仰角和攻角；k为诱导阻力系数；α为俯仰舵偏角，即本文所需优化设计的程序角；Cx0、Cx0(α)分别为弹翼整体和舵的零升阻力系数；Cyb′、Cyα′分别为弹翼整体和舵的升力系数导数；m′z、m′zz分别为弹翼整体和舵的俯仰力矩系数导数；Lα为俯仰舵压心到全弹质心的距离；L为弹长；在计算过程中，零升阻力系数、升力系数导数和俯仰力矩系数导数通过数据表形式插值获得；ρ为大气密度，大气模型参考文献[8]。

3　最优控制模型建立

靶弹平飞段平飞高度和平飞时间的优化控制，可以选用射程最大化、平飞段射程占总射程比重最大及平飞段高度与预定平飞高度之间的高度差最小化来进行衡量，选取目标函数如(3)式：

(3)

式中：t0、tf分别为弹道发射点和落点时刻；t1、tf1分别为平飞段开始和结束点时刻；k1、k2、k3分别为目标函数中各项所占的权重系数，不同的权重系数取值对优化结果影响很大，应结合不同的工程实际需要设置不同的权重系数，得到适当的优化结果；Rmax为无控火箭弹所能达到的最大射程；Herr为平飞段平飞高度所能允许的波动误差。通过选取不同的平飞开始时间即可形成如图1(a)和图1(b)所示的弹道形式。

靶弹弹道优化过程中满足如下约束条件：

1)端点约束：以火箭靶弹起始发射点条件为起点约束条件，落点性能条件为终端约束条件。

初始约束：v=v0，θ=θ0，x=x0，y=y0；

终端约束：v=vtf，θ=θtf，x=xtf，y=ytf.

2)过程约束：如(1)式。

3)平飞段约束：简易控制火箭靶弹平飞段可看作以一定的高度等高飞行，或者飞行过程中弹道倾角θ恒为0°. 在平飞过程中，由于速度不断地减小，需实时地改变俯仰舵偏角的大小来获得较大的升力以平衡重力，但是若靶弹严格以一定高度平飞，飞行速度在阻力的作用下衰减较快，为平衡重力需增大俯仰舵偏角而产生较大的飞行攻角，使得火箭靶弹的稳定性改变，不利于控制系统的控制，所以本文近似认为平飞段是在满足一定幅值的平飞高度波动飞行。平飞示意图如图2所示。

平飞段满足约束如下所示：

θpf=0°±θerr,

(4)

Hpf=H0±Herr,

(5)

vmin≤vpf≤vmax,

(6)

式中：θpf、Hpf、vpf分别为平飞时的弹道倾角、平飞高度和平飞速度；θerr为平飞所允许的弹道倾角。

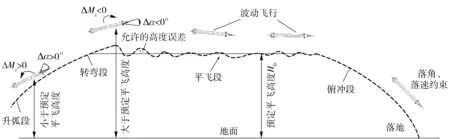
图2　平飞段供靶弹道Fig.2　The trajectory for target of level flight

4)控制量约束：控制量满足控制系统所能提供的控制范围：

|u|≤U，U>0.

(7)

5)为避免俯仰角变换频率较快，引起靶弹飞行失稳，在飞行中需对俯仰角速度进行约束：

|ω|≤W，W>0.

(8)

4　程序角优化问题求解

4.1运动参数化

第3节中最优程序角的优化设计问题可作为一般最优控制问题：寻找控制变量u(t)∈Rm，最小化具有一般性的Bolza型性能指标：

(9)

式中：状态变量x(t)∈Rn、初始时间t0和终端时间tf，满足动力学微分方程约束

(10)

边界条件

Φ(x(t0),t0,x(tf),tf)=0.

(11)

路径约束

C(x(t),u(t),t)≤0.

(12)

将(10)式进行泰勒展开，忽略高阶项，可得

(13)

式中：A(t)=fx(xp,up)，B(t)=fu(xp,up)，xp、up分别为状态变量和控制变量，结合(2)式火箭靶弹纵向平面内动力学模型，A(t)、B(t)可写为

(14)

(15)

δu)+λT(A(t)δx+B(t)δu),

(16)

式中：λ为协态向量；Q、R为n维半正定矩阵。为使性能函数满足最优解的1阶必要条件，则

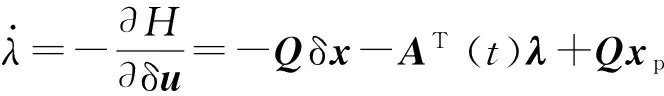
(17)

(18)

靶弹弹道优化设计可转换为两点边值问题,

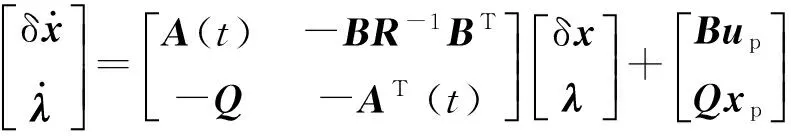
(19)

Gauss伪谱法通过将状态变量和控制变量在一系列的Gauss点上离散，可将两点边值最优控制问题转换为受一系列代数约束的参数优化问题，其求解步骤：

1)时域变换。设火箭靶弹飞行时间t∈[t0,tf]，将时间离散到τ∈[-1，1]，对时间t变换如下：

(20)

2)状态变量与控制变量离散。取K个Legendre-Gauss点为Gauss伪谱法的离散点，即离散点为K阶Legendre多项式PK(τ)的根，

(21)

(22)

(23)

4)离散条件下的终端状态约束。Gauss伪谱法中的节点包括K个配点(τi，…，τk)和初始点τ0≡-1以及终点τf≡1. (22)式未定义终端状态Xf，终端状态也应满足动力学方程约束：

(24)

将终端状态约束条件离散并用Gauss积分近似:

X(τf)=X(τ0)+

(25)

5)动力学方程约束转换为代数约束。对(22)式求导可得状态变量导数，将动力学方程约束转换为代数约束，即

(26)

式中：微分矩阵D∈RK×(K+1)，可离线确定

(27)

式中:τk(k=1，2，…，K)属于集合κ中的点；τi(i=1，2，…，K)属于集合κ0={τ0，τ1，…，τk}.

这样，最优控制问题的动力学微分方程约束即转换为代数约束:

(28)

6)基于Gauss积分的近似性能指标函数。将Bolza型性能指标函数中的积分项用Gauss积分来近似，得到在Gauss伪谱法中的近似性能指标函数：

(29)

综上6个步骤，Gauss伪谱法将连续最优控制问题离散并转换成为非线性规划问题。详细步骤参考文献[9-13]。

4.2参数化求解

图3为弹道优化问题的一般流程，通过4.1节将运动方程进行参数化并转换成一系列非线性规划方程，利用序列二次规划法对此非线性规划方程组进行求解。序列二次规划法的基本思路为：在每一个迭代步通过求解一个二次规划子问题来确定一个下降方向，减少价值函数来取得步长，重复这些步骤直到求得问题的解，其基本形式[14]可表示为

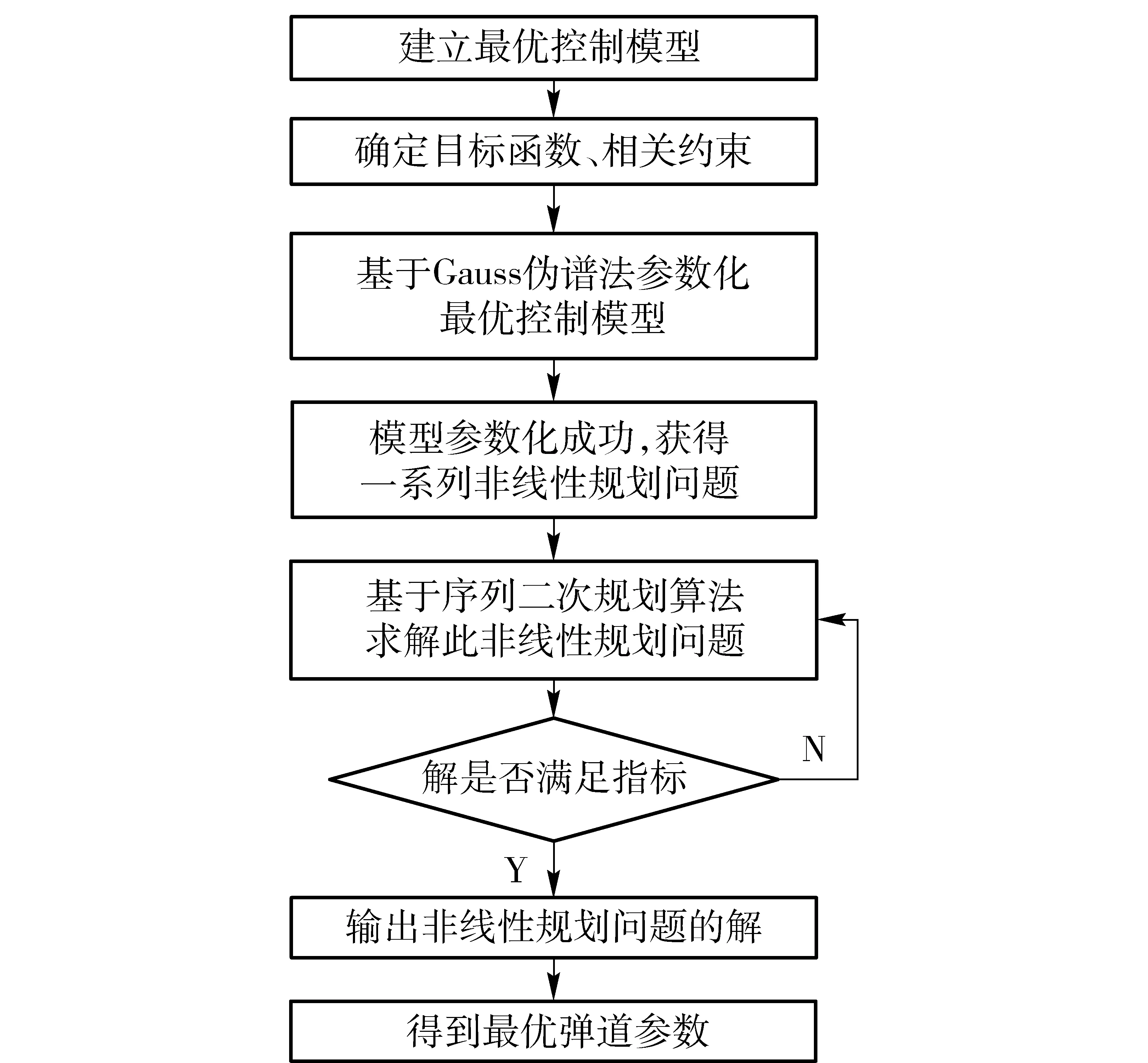
图3　弹道优化流程Fig.3　Optimization process of trajectory

(30)

(31)

sk=xk+1-xk,

(32)

(33)

zk=θkyk+(1-θk)Bksk,

(34)

(35)

5　仿真计算

以某型火箭靶弹的数据为例，将火箭靶弹主动段末速度等效为炮口速度，质量m0=800 kg，出炮口速度v0=1 650 m/s，起始射角35°，气动数据通过气动软件计算获得，飞行最大允许攻角δ<5°，舵偏角|α|≤20°，平飞高度10 km，允许上下浮动100 m，平飞弹道倾角允许上下浮动5°，落角θf≥30°，超音速指标满足飞行速度v≥400 m/s，终端时间自由。

利用上述伪谱法原理，将方程组参数化，编制程序，选取插值点数为160，权重系数k1=10，k2=k3=1，在计算机内存为8 G，主频为2.66 GHz四核环境下，计算耗时10.289 491 s. 表1和图4为相同初始条件下无控弹道和最优程序角作用下的弹道参数对比。

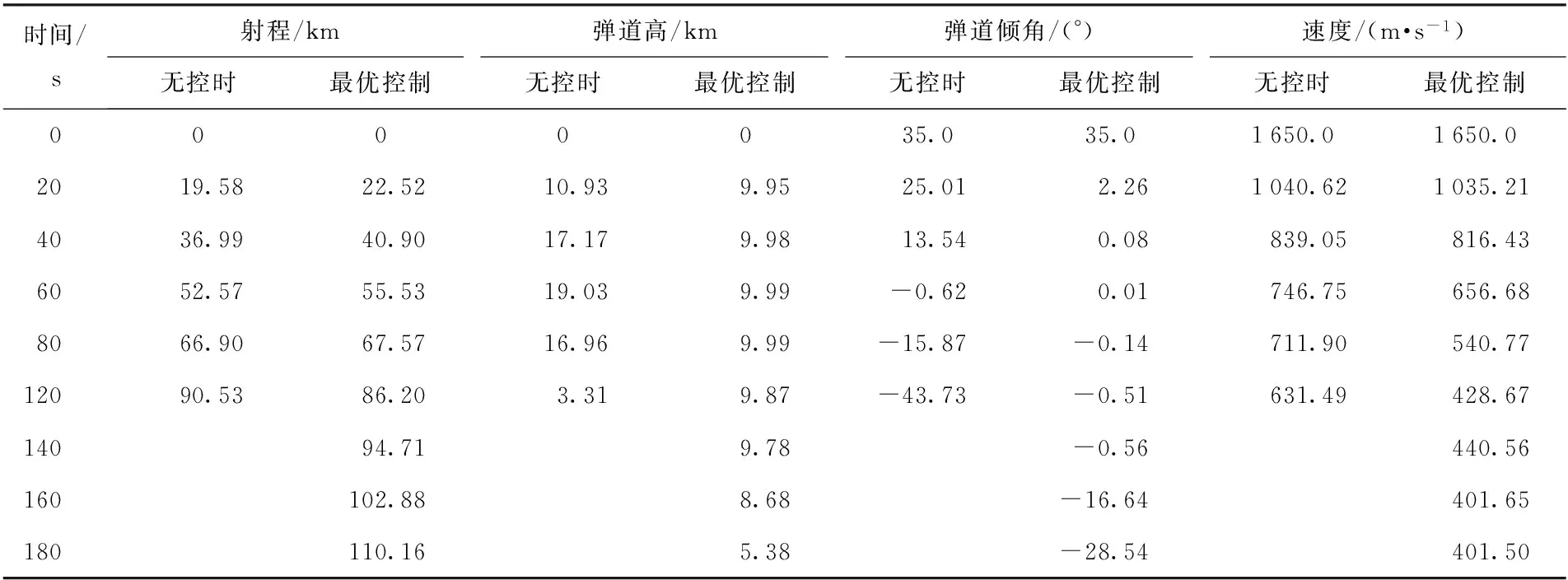
表1　控制前后弹道参数对比

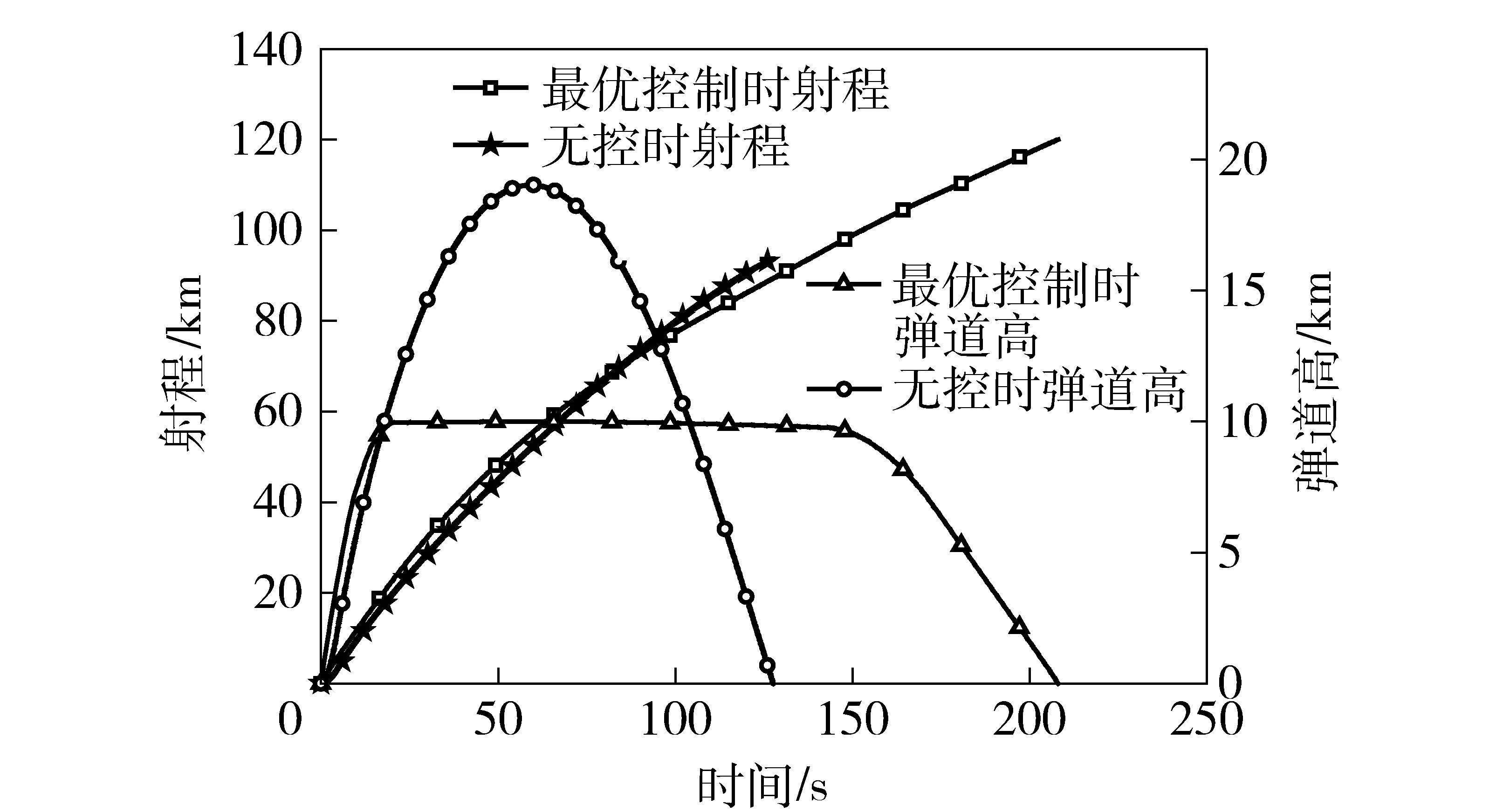
图4　控制前后射程和弹道高对比Fig.4　Comparison of height and range

从图4和表1中数据可以看出，在优化设计后的俯仰舵偏角的作用下，射程和滞空时间相比无控弹道明显增加，弹道高按照预定的高度相比无控弹道更为平直，无控抛物线弹道特性明显被改善。

图5所示为优化设计后的俯仰舵偏角曲线和攻角曲线。结合图4、图5可知，在弹道上升段，火箭靶弹在一个大的负舵偏角下飞行，其目的是使靶弹整体形成一个负攻角产生向下的升力，将弹道在预定的平飞高度尽早拉平。当火箭靶弹进入平飞阶段后，随着速度的减小，俯仰舵以正的舵偏角产生向上的升力抵消重力实现平飞。平飞阶段结束后，俯仰舵在图5舵偏角规律下满足落点速度和落角大小的约束飞行。整个飞行过程中产生的攻角绝对值小于2°，满足飞行稳定性的要求。

图5　舵偏角和攻角曲线Fig.5　Rudder angle and attack angle curves

图6、图7为相同起始条件、飞行约束条件及落点约束条件下，采用本文方法与经典俯仰程序角设计方法所优化得到的弹道结果对比曲线。由图6、图7可知，本文方法优化所得平飞段平飞高度、弹道倾角基本维持在10 km和0°，满足平飞约束条件。落角和落点速度为30°、400 m/s满足落点约束条件。相比经典设计方法，采用本文方法的火箭靶弹供靶弹道更为平直；在满足供靶指标的前提下，其供靶时间136.8 s，也较经典设计方法下87.7 s更长，具有更好的平飞供靶性能。同时，在起始条件、终端约束及飞行指标相同的条件下，本文所述方法仅选取俯仰舵偏角为优化变量，参数设置简单，计算效率高，而经典俯仰程序角设计方法则需对(1)式中5个参数变量组合进行寻优，计算效率明显降低，计算结果是否收敛于最优解难以得到保证。

图6　弹道高和弹道倾角曲线Fig.6　Height and trajectory obliquity curves

图7　弹道高和速度曲线Fig.7　Height and velocity curves

为验证本文方法的鲁棒性，在火箭靶弹质量、炮口条件、飞行约束条件及目标函数相同的情况下，研究参数不确定性对系统控制量变化规律及最优弹道的影响，图8、图9为不同射角下俯仰舵偏角变化曲线和弹道高曲线。

图8　不同射角下舵偏角变化曲线Fig.8　Rudder angle curves at different fire angles

图9　不同射角下弹道高曲线Fig.9　Height curves at different fire angles

任取射角为35°时优化得到的舵偏角曲线和弹道高曲线，并以此舵偏角曲线作为初始射角为36°时的控制曲线，计算得到两种不同起始射角下的弹道高误差曲线，如图10所示。

图10　弹道高误差曲线Fig.10　Height error curve

由图8和图9可以看出，在不同的射角下，其舵偏角变化规律和弹道高曲线分别基本一致。图10表明，利用Gauss伪谱法获得的俯仰舵偏角变化规律用于起始射角变化后所得的弹道高曲线仍满足供靶指标要求，这是因为Gauss伪谱法是一种采用全局配点的优化方法，可以很好地避免了模型等参数不确定性的干扰，具有良好的鲁棒性。

图11是在改变起始发射角及调整平飞段起控时间后，利用本文方法所获得如图1(b)所示的低空供靶弹道，包含弹道高、速度与弹道倾角变化曲线。对比图6所示弹道，图11所示的平飞供靶时间明显小于图6所示弹道的平飞供靶时间，但是在满足速度指标下，图11所示弹道在过弹道顶点后至平飞供靶开始之间，可模拟目标的俯冲特性，从而实现一靶多用。

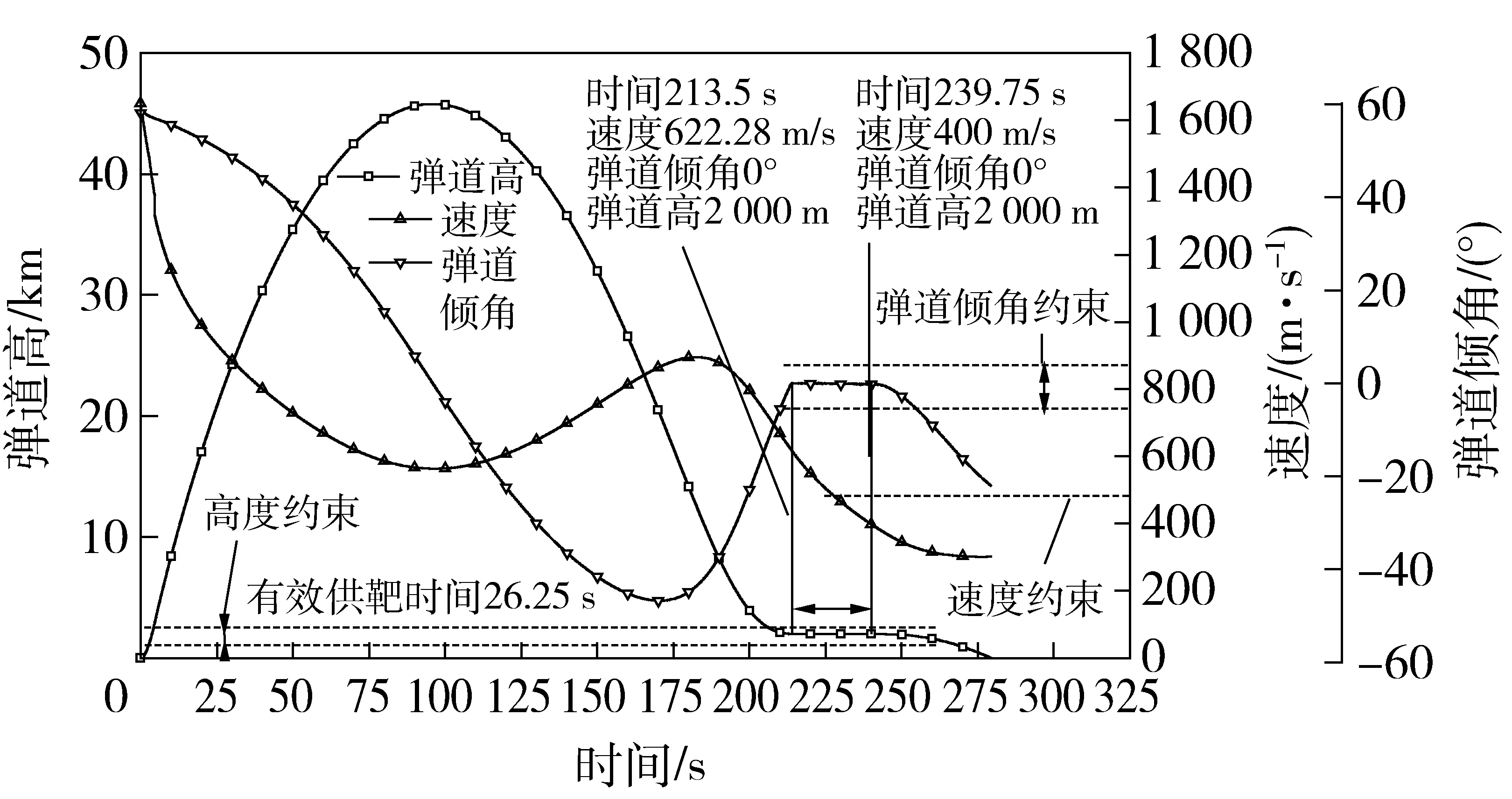
图11　低空平飞供靶弹道Fig.11　Level flight trajectory for target at low-altitude

为简化火箭靶弹升弧段俯仰舵偏角设计，通过采用使靶弹升弧段任意时刻满足升阻比最大，并以平飞滑翔开始时飞行动能最大为优化目标的优化策略，利用成熟的优化方法优化获得火箭靶弹最优射角和升弧段起控时间，进而以此射角和起控时间为初始条件，采用本文方法对俯仰舵偏角进行优化，快速获得满足供靶指标的供靶弹道。因高空舵控效率降低，平飞供靶性能可允许在供靶阶段内具有一定的弹道落差，实现准平飞供靶。采用上述火箭靶弹数据，在15 km高空优化火箭靶弹准平飞供靶弹道，高空供靶落差不大于2 km，其他约束条件及供靶性能指标同上。采用粒子群算法优化在射角范围θ0∈[30°,60°]，升弧段起控时刻tc∈[5 s,8 s]，优化获得起始射角和起控时间分别为50.56°，8 s. 以此为初始计算条件，采用本文俯仰舵偏角优化方法，优化获得15 km高空下准平飞供靶弹道如图12所示，供靶过程优化耗时13.58 s.

图12显示，利用本文提出的方法，能够在高度为15 km下快速优化出满足供靶指标的供靶弹道，供靶时间为122.81 s，同时满足落点性能约束。

图12　高空准平飞供靶弹道Fig.12　Level flight trajectory at high-altitude

6　结论

针对超音速靶弹平飞段平飞性能问题，分析了超音速靶弹平飞段的相关约束，建立了火箭靶弹程序角设计模型，通过Gauss伪谱法将此最优控制问题转换成一系列非线性规划问题。以最大射程、平飞段射程所占总射程的比重及平飞段飞行高度和指定平飞高度差最小为目标，利用序列二次规划法求解得到了实现靶弹平飞的最优程序角变化规律及最优方案供靶弹道，系统具有良好的鲁棒性、相比经典俯仰程序角设计方法具有设置参数与优化变量少，计算时间短等特点，能够为简易控制超音速靶弹平飞供靶方案制导设计提供相关的参考。

References)

[1]张邦楚, 韩子鹏, 范雁飞. 巡航导弹模拟靶平飞弹道设计[J].弹道学报, 2003, 15(2): 28-33.

ZHANG Bang-chu, HAN Zi-peng, FAN Yan-fei. Design of the level trajectory of cruise missile simulated target [J]. Journal of Ballistics, 2003, 15(2):28-33. (in Chinese)

[2]李晓斌, 王永杰, 孙晓峰. 简易控制火箭靶弹总体设计[J]. 弹道学报, 2010, 22(1): 41-44.

LI Xiao-bin, WANG Yong-jie, SUN Xiao-feng.System design of simple control rocket target[J]. Journal of Ballistics, 2010, 22(1):41-44. (in Chinese)

[3]霍鹏飞, 施坤林, 苑伟政. 基于极大值原理的弹道修正引信弹道优化控制研究[J]. 兵工学报, 2007, 27(3): 301-304.

HUO Peng-fei, SHI Kun-lin, YUAN Wei-zheng. Research on trajectory controlled optimization for trajectory correction fuze using maximum principle[J]. Acta Armamentarii, 2007, 27(3): 301-304. (in Chinese)

[4]李永远, 姜毅, 高伟涛, 等. 间接法求解具有最大横程的再入轨迹[J]. 北京理工大学学报, 2013, 33(7): 665-668.

LI Yong-yuan, JIANG Yi, GAO Wei-tao, et al. Indirect method for solving the reentry trajectory with maximum cross range[J]. Transactions of Beijing Institute of Technology, 2013, 33(7):665-668. (in Chinese)

[5]李柯, 聂万胜, 冯必鸣. 助推- 滑翔飞行器规避能力研究[J]. 飞行力学, 2013, 31(2): 148-156.

LI Ke, NIE Wan-sheng, FENG Bi-ming. Research on elusion capability of boost-glide vehicle[J]. Flight Dynamics, 2013, 31(2): 148-156. (in Chinese)

[6]水尊师, 周军, 葛致磊. 基于高斯伪谱方法的再入飞行器预测校正制导方法研究[J]. 宇航学报, 2011, 32(6): 1249-1254.

SHUI Zun-shi, ZHOU Jun, GE Zhi-lei. On-line predictor-corrector reentry guidance law based on Gauss pseudospectral method[J]. Journal of Astronautics, 2011, 32(6): 1249-1254. (in Chinese)

[7]Huntington G T. Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems[D]. MA: Massachusetts Institute of Technology, 2007: 23-49.

[8]林献武. 高空环境下弹箭的弹道特性研究[D].南京: 南京理工大学, 2009: 9-13.

LIN Xian-wu. A research on the ballistic characteristics of projectile flying at high altitude environment[D].Nanjing: Nanjing University of Science and Technology, 2009: 9-13. (in Chinese)

[9]Garg D, Hager W W, Rao A V. Pseudospectral methods for solving infinite-horizon optimal control problems[J].Automatica, 2011, 47(4): 829-837.

[10]Maleki M, Hashim I. Adaptive pseudospectral methods for solving constrained linear and nonlinear time-delay optimal control problems [J].Journal of the Franklin Institute, 2014, 351(2): 811-839.

[11]Rao A V, Clarke K A. Performance optimization of a maneuvering re-entry vehicle using a legendre pseudospectral method[C]∥2002 AIAA Atmospheric Flight Mechanics Conference. Monterey, US: American Institute of Aeronautics and Astronautics, 2002.

[12]Rao A V, Benson D A, Darby C. Algorithm 902: GPOPS, A MATLAB software for solving multiple-phase optimal control problems using the gauss pseudospectral method[J].ACM Transactions on Mathematical Software, 2010, 37(2): 1-39.

[13]Garg D, Rao A V, Hager W W. Gauss pseudospectral method for solving infinite-horizon optimal control problems[C]∥AIAA Guidance, Navigation, and Control Conference.Toronto, Ontario, Canada Toronto: American Institute of Aeronautics and Astronautics, 2010: 1-9.

[14]郑总准, 吴浩, 王永骥. 基于序列二次规划算法的再入轨迹优化研究[J]. 航天控制, 2009, 27(6): 8-13.

ZHENG Zong-zhun, WU Hao, WANG Yong-ji.Reentry trajectory optimization using sequential quadratic programming[J]. Aerospace Control, 2009, 27(6): 8-13. (in Chinese)

Research on a Program Angle Optimization Method for Supersonic Rocket Target

SHEN Guan-jun1, FENG Shun-shan2, CAO Hong-song1

(1.School of Mechatronics Engineering, North University of China, Taiyuan 030051, Shanxi, China; 2.State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)

An optimization method of pitch program angle is proposed for the optimization problems of level flight trajectory of supersonic rocket target. Considering the initiation and impact point of rocket target and the level flight state constraints, the pitch program angle optimization model is built on the longitudinal flight plane of rocket target. The Process constraints are transformed to the pitch program angle constraints, and the optimal control problems are translated to the nonlinear programming problems based on Gauss pseudo spectral method. And then the nonlinear programming problems are solved by sequential quadratic programming method. Simulation results show that this proposed method can quickly obtain the optimal program pitch angle, and has good robustness.

ordnance science and technology; supersonic rocket target； level flight trajectory； program angle optimization； Gauss pseudo spectral method

2014-05-06

兵器“十二五”预先研究支撑基金项目(62201070503)

沈冠军(1987—)，男，博士研究生。E-mail:mmlife@126.com;

冯顺山(1952—)，男，教授，博士生导师。E-mail:ssfeng@bit.edu.cn

TJ013.2

A

1000-1093(2015)04-0644-09

10.3969/j.issn.1000-1093.2015.04.011