固定翼双旋弹动力学特性分析

许诺， 于剑桥， 王亚飞， 王林林

(北京理工大学 宇航学院， 北京 100081)



固定翼双旋弹动力学特性分析

许诺， 于剑桥， 王亚飞， 王林林

(北京理工大学 宇航学院， 北京 100081)

固定翼双旋弹作为一种特殊的弹道修正弹，在飞行过程中其前体弹道修正引信(CCF)和后体以不同转速绕弹轴旋转。根据固定翼双旋弹气动不对称的特性，推导出固定翼双旋弹的动力学模型，经过模型简化，得到其非齐次角运动方程，根据这个角运动方程对角运动特性和飞行稳定性进行了分析。结果显示：当CCF转速固定时，转速的大小和滚转的方向都会影响弹体的角运动特性，由于弹体的共振，不合理的转速可能引起角运动的不稳定；当CCF转角固定时，弹体可以获得与CCF的鸭翼安装角近似呈正比的弹道修正能力。对固定翼双旋弹的飞行稳定性判据进行了研究，飞行稳定性判据为固定翼双旋弹前后体转速和初始射角的设计提供了参考。

兵器科学与技术； 固定翼双旋弹； 弹道修正引信； 非齐次角运动方程； 弹道修正能力； 稳定性判据

0　引言

弹道修正弹是将原来的炮射弹药加装弹道修正模块，使弹丸在空中飞行时可以控制，以提高炮弹命中率的一类新型弹药。其基本原理是在弹丸发射前根据探测到的炮位坐标、目标坐标等信息预先装定标称弹道信息，弹丸发射后探测飞行弹丸的实际弹道，将此实际弹道与预先装定的标称弹道进行比较，结合更新的目标信息计算出弹道偏差，并根据偏差的大小控制弹上的修正机构进行距离和方向修正。弹道修正弹介于无控弹药和导弹之间，没有寻的能力，其成本低、毁伤率高、效费比高，因而发展相当广泛和迅速。

其中双旋修正弹极具发展潜力，其由前体弹道修正引信(CCF)和后体两部分组成，二者间采用滚动轴承连接，飞行中分别以低速和高速旋转。早在2000年Costello等[1]就对双旋弹进行了动力学建模；Wernert等[2-3]和Theodoulis等[4-5]在Costello等[1]所提出双旋弹模型的基础上，对前体鸭舵偏转角可控的双旋弹进行了稳定性分析和控制特性的研究；郝永平等[6]和纪秀玲等[7]提出了固定翼双旋弹的修正模型并进行了气动特性分析；常思江等[8]对固定翼双旋弹进行了初步建模和仿真。相比于鸭舵偏转角可控的双旋弹，固定翼双旋弹具有执行机构简单、修正原理简明等优点，成为当前弹道修正弹研究的热点之一。

目前国内外对固定翼双旋弹的研究相对较少，多集中于修正原理及气动特性的分析，动态特性及弹道特性研究的手段也仅局限于数值仿真或针对特定情况进行简化分析，缺乏进一步的解析分析结果，所得结论不具有一般性。本文基于双旋弹的动力学模型，得到了固定翼双旋弹的非齐次攻角运动方程，并分别针对CCF匀速滚转及停留在任意角位置两种典型运动情况进行了分析。

1　固定翼双旋弹动力学建模

固定翼双旋弹是采用隔离式具有固定偏转角的鸭翼对弹道进行纵向和横向修正的弹道修正弹。其弹体分为两部分：以几百弧度每秒的速度高速旋转并装有战斗部的后体以及与后体分离旋转并装有制导控制硬件、软件的前体CCF. 4片鸭翼布置在炮弹头部的CCF上，其中一对具有固定的差动偏转角，另一对具有固定的同向偏转角，其结构示意图如图1所示。带有4片鸭翼的CCF与后体之间通过轴承隔离开，炮弹发射以后，具有固定差动偏转角的鸭翼使整个CCF减旋，而炮弹主体仍以高速旋转，保证弹体陀螺稳定。减旋后CCF的转速较低，但仍能保证4片鸭翼对弹体的平均作用力和力矩为0. 当需要对弹道进行某方位修正时，通过给电枢供电产生扭矩，将一对具有同向偏转角的鸭翼制动在所需控制力或力矩的方位，从而实现对弹道的修正。

图1　CCF结构示意图Fig.1　The configuration of CCF

动力学建模用到的坐标系有：地面坐标系Oxtytzt、弹道坐标系Oxcyczc、弹轴坐标系Oξηζ[9-10]和修正引信坐标系Oxfyfzf. 修正引信坐标系Oxfyfzf的定义如下：

原点位于弹体质心，Oxf轴沿CCF轴向，与弹轴重合，Oyf轴与同向偏转的鸭翼所产生的附加升力方向相一致，Ozf按右手法则确定。定义δw为翼面偏转角度，表征同向鸭翼平面相对弹轴方向旋转的角度。定义Oyf轴与Oη轴的夹角为前体修正引信滚转角γf，该角度表征同向鸭翼产生的升力相对于竖直平面偏转的角度。方向从弹尾看，由Oη轴顺时针转至Oyf轴为正。示意图如图2所示。

图2　Oxfyfzf坐标系和CCF滚转角γf示意图Fig.2　OxfYfZf coordinate system and roll angle of CCF γf

固定翼双旋弹角运动方程如下所示：

(1)

(2)

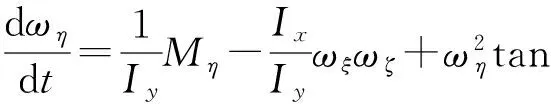
(3)

(4)

式中：ωξ、ωη、ωζ分别为弹体角速度在弹轴坐标系各轴上的投影；ωξ为固定翼双旋弹的合转速；m为弹体质量；v为弹体速度大小；φpg和εpg分别弹轴相对于地面坐标系的高低角和方位角；φvg和εvg分别为速度轴相对地面坐标系的高低角和方向角；Ix为弹体轴向转动惯量；Iy为弹体法向转动惯量；Fyc和Fzc分别为Oyc和Ozc方向的气动力；Mη和Mζ分别为Oη和Oζ方向的气动力矩。其中，气动力和力矩分别为

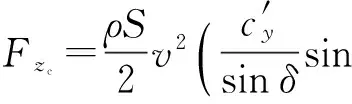
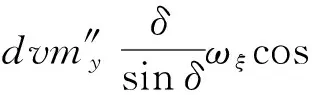
式中：ρ为空气密度；S为参考面积；d为弹体直径；l为参考长度；c′y为弹体升力系数；c″z为马格努斯力系数导数；c′w为翼面升力系数；m′z为弹体俯仰力矩系数；m′zz为弹体阻尼力矩系数；m″y为马格努斯力矩系数导数；m′w为翼面产生俯仰力矩系数；δe为高低攻角；δd为方向攻角；δ为合攻角。

考虑到固定翼双旋弹的角运动是在理想弹道周围进行的，理想弹道的弹道倾角和弹道偏角分别为θ和ψ，其中ψ可近似为0°. 则弹轴相对于理想弹道的高低角和方位角分别为φpc=φpg-θ和εpc=εpg，速度轴相对理想弹道的高低角和方位角分别为φvc=φvg-θ和εvc=εvg.

(5)

(6)

(7)

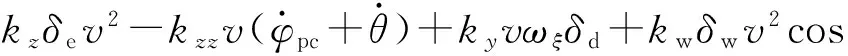
(8)

将(5)式～(8)式写为复数形式，忽略重力侧向力(gsinθΨ=0)，可得

(9)

(10)

(11)

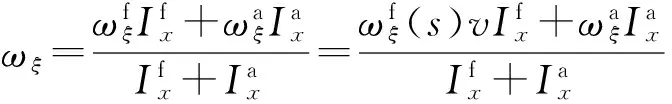
Δ″+(H-iP)Δ′-(M+iPT)Δ=

(12)

2　角运动特性分析

Δ=Δ1+ΔP2+ΔP3，

(13)

齐次方程的通解为

Δ1=C1eiω1s+C2eiω2s，

(14)

由于H≪P，M2≫P2T2，由重力引起的动力平衡角的表达式可近似表示为

(15)

考虑由CCF引起的角运动，角运动方程可写为

Δ″+(H-iP)Δ′-(M+iPT)Δ=

(16)

式中：γf是对弧长s的函数。

可用常数变易法求得(16)式的特解：

(17)

在飞行过程中，固定翼双旋弹的CCF大体处于两种状态：周期旋转状态和转角固定状态。CCF不同的运动状态对应着不同的角运动特性。下面针对CCF的这两种状态对CCF产生的动力平衡角和弹道特性进行分析。

2.1CCF周期旋转

Δ″+(H-iP)Δ′-(M+iPT)Δ=

(18)

(19)

将(19)式代入方程(18)式中，可解出

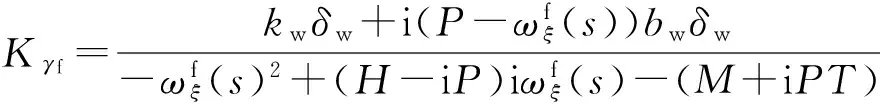
(20)

(21)

图3　|Kγf|随变化趋势图Fig.

(22)

这表示攻角振幅与飞行距离呈正比，攻角运动会随着飞行时间的增加而发散，是一种不稳定的运动状态。

图4　CCF以不同转速旋转时的攻角运动曲线Fig.4　Angle of attack curves when the CCF rolls at different roll rates

攻角的周期变化会引起速度方向的周期变化，进而引起弹道的螺旋运动。若忽略翼面附加升力及马格努斯力对速度的影响，仅考虑较大的弹体升力项，则(19)式代入(9)式可得

(23)

则由ΔP3产生的速度垂直分量v⊥=vΨP3，弹体法向弹道的运动距离为

(24)

(24)式中，排除初始条件的影响，仅保留周期运动项，可得弹体螺旋运动的旋转半径为

(25)

这与前文分析和仿真的结果一致，CCF滚转的角速度及方向对弹道特性具有十分重要的影响。对于滚转稳定弹体，由于by、kw和bw非常小，弹体的螺线运动很难在仿真中表现出来。

2.2CCF转角固定

Δ″+(H-iP)Δ′-(M+iPT)Δ=

(kwδw+iPbwδw)eiγf.

(26)

(26)式中，等号右边是定值，特解ΔP3可写为

(27)

由于ΔP3是CCF的鸭翼在平衡状态下产生的攻角分量，故可把ΔP3叫做鸭翼产生的动力平衡角。将(27)式分母实数化：

(28)

式中：

(29)

将重力产生的动力平衡角和鸭翼产生的动力平衡角相加，则(12)式特解的近似表达式为

ΔP=ΔP2+ΔP3=δeP+iδdP=

(30)

将(30)式分解成实数部分和虚数部分后，可得纵向与侧向的动力平衡角表达式如下：

(31)

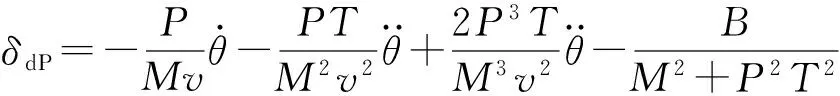
(32)

将由(31)式和(32)式算出的动力平衡角与六自由度弹道仿真得到的攻角进行对比，图5为CCF滚转角分别取0°、90°、180°、270°时的对比曲线，其中δeP和δdP为(31)式、(32)式算出动力平衡角，δeS和δdS为六自由度弹道仿真所得攻角。由图5可见，(31)式、(32)式得出的动力平衡角与弹道仿真得到的攻角差异不大，证明了该计算方法的合理性与准确性。

图5　CCF固定在不同角位置时的攻角曲线Fig.5　Angle of attack curves when CCF is fixed at different roll angles

CCF滚转角固定时，由CCF引起的附加动力可分为两部分：由翼面直接产生的气动力和翼面诱导攻角产生的升力。二力的合力将使得弹丸产生法向加速度，导致弹道弯曲，从而进行弹道修正。

根据前文分析，翼面产生的动力平衡角分量ΔP3为一复攻角，其模值和幅角分别为

(33)

(34)

由(34)式可见，随着γf的变化，ΔP3在复平面上的轨迹近似为以原点为中心的圆。ΔP3的幅角与γf始终相差一个固定角度

(35)

对于轴对称弹丸，ΔP3会产生附加弹体升力

ΔY=mv2byΔP3.

(36)

此外，翼面升力表示在复平面上，可近似表示为

Yw=mv2bwδweiγf.

(37)

附加升力ΔY与翼面升力Yw合力FC的大小表征了弹道修正能力的强弱。通过矢量运算，FC的模值和幅角分别为

|FC|=mv2|δw|·

(38)

γC=γf+arccos

(39)

可以通过调整修正引信滚转角γf，使合力FC在飞行过程中始终指向固定的方向，弹丸在该方向上将具有最大修正能力。

实际上，对于固定翼双旋弹，通常情况下bw、T数值较小，若略去这两项，有

γC=γf+π.

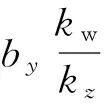
为了验证固定翼双旋弹的最大修正能力，进行了六自由度有控刚体弹道仿真。在δw=2.5°和δw=5.0°两种情况下，从不同时刻开始调整γf使FC指向侧向，侧向修正距离如图6所示。结果表明，侧向的修正距离大致与CCF同向翼面的安装角δw呈正比；起控越早，弹道修正能力越强。仿真结果与前面的理论分析一致。

图6　不同起控时刻的最大修正区域Fig.6　The maximum correction distance of projectile at different starting control moments

3　飞行稳定性判据

为了研究固定翼双旋弹在飞行过程中的稳定性判据，引入陀螺稳定因子和动态稳定因子的概念：

动态稳定因子Sd=(2T-H)/H.

动态稳定因子Sd本质上取决于马格努斯力矩T与赤道阻尼力矩H之比。

(40)

(41)

当弹体合转速满足|ωξ|>ωg时，则弹丸满足陀螺稳定性；当满足|ωξ|>ωd时，则弹丸满足动态稳定性。

当CCF转角固定时，由于固定翼双旋弹是静不稳定旋转弹，动力平衡角过大将使弹体飞行特性变坏，散布增大，甚至射程大减。为让固定翼双旋弹具有良好的追随稳定性，必须限制动力平衡角的大小。因动力平衡角的最大值出现在弹道顶点附近，故只须限制最大射角弹道顶点处动力平衡角的高低分量δeP和方向分量δdP小于限制值δpm即可，即

上式即为固定翼双旋弹的追随稳定性判据，一般δpm取12°～15°.

4　结论

本文建立了固定翼双旋弹的动力学模型，简化得到非齐次攻角运动方程，基于该运动方程进行的角运动特性分析及飞行稳定性分析结果如下：

1) 当CCF匀速旋转时，攻角运动将在二圆运动的基础上叠加一个受迫振动。受迫振动的频率与CCF的转速相同，其振幅则与CCF的转速和二圆运动的两个频率有关。CCF转速的不合理可能引起攻角运动的发散，而保持CCF旋转方向与弹体旋转方向相反则可以有效避免这一问题。

2) 当CCF转角固定时，翼面产生的气动力矩将导致弹体产生附加动力平衡角，进而产生附加升力，附加升力与翼面升力的合力将导致速度大小和方向的变化。因此可以通过调整CCF的滚转角改变弹道落点。文中推导出附加升力与翼面升力合力的方向及大小，仿真结果表明，弹丸的弹道修正能力与CCF上翼面的安装角呈正比，与翼面升力系数和弹体附加升力系数的差值呈正比。

3) 为了使固定翼双旋弹能够稳定飞行，应设计合适的前体转速和后体转速以满足弹体在飞行过程中的陀螺稳定性和动态稳定性；并可根据固定翼双旋弹的追随稳定性判据对初始射角进行设计和优化。

References)

[1]Costello M, Peterson A. Linear theory of a dual-spin projectile in atmospheric flight[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(5): 789-797.

[2]Wernert P. Stability analysis for canard guided dual-spin stabilized projectiles[C]∥Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit. Honolulu, Hawaii: AIAA,2009.

[3]Theodoulis S, Morel Y,Wernert P. Modelling and stability analysis of the 155 mm spin-stabilised projectile equipped with steering fins[J]. International Journal of Modelling, Identification and Control, 2011, 14(3): 189-204.

[4]Theodoulis S, Wernert P. Flight control for a class of 155 mm spin-stabilized projectiles with course correction fuse (CCF)[C]∥AIAA Guidance, Navigation and Control Conference and Exhibit. Portland, OR: AIAA,2011.

[5]Theodoulis S, Gassmann V, Wernert P, et al. Guidance and control design for a class of spin-stabilized fin-controlled projectiles[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(2): 517-531.

[6]郝永平, 孟庆宇, 张嘉易. 固定翼二维弹道修正弹气动特性分析[J]. 弹箭与制导学报, 2012, 32(3): 171-173.

HAO Yong-ping, MENG Qing-yu, ZHANG Jia-yi. Aerodynamic characteristic analysis on two-dimensional trajectory Corrector shell with fixed-wing[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(3): 171-173.(in Chinese)

[7]纪秀玲, 王海鹏, 曾时明, 等. 可旋转鸭翼对旋转弹丸纵向气动特性的影响[J]. 北京理工大学学报, 2011, 31(3): 265-268.

JI Xiu-ling, WANG Hai-peng, ZENG Shi-ming, et al. CFD prediction of longitudinal aerodynamics for a spinning projectile with fixed canard[J]. Transactions of Beijing Institute of Technology, 2011, 31(3):265-268. (in Chinese)

[8]常思江, 王中原, 刘铁铮. 鸭式布局双旋弹飞行动力学建模与仿真[J/EB]. [2013-01-01].http:∥www.paper.edu.cn.

CHANG Si-jiang, WANG Zhong-yuan, LIU Tie-zheng. Modeling and simulation of flight dynamics for dual-spin projectiles equipped with canards[J/EB]. [2013-01-01].http:∥www.paper.edu.cn. (in Chinese)

[9]韩子鹏. 弹箭外弹道学[M]. 北京: 北京理工大学出版社, 2008.

HAN Zi-peng. Rocket exterior ballistics [M]. Beijing: Beijing Institute of Technology Press,2008. (in Chinese)

[10]钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京：北京理工大学出版社, 2008.

QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan. Missile flight mechanics[M]. Beijing: Beijing Institute of Technology Press,2008. (in Chinese)

Analysis of Dynamic Characteristics of Fixed-wing Dual-spin Projectiles

XU Nuo, YU Jian-qiao, WANG Ya-fei, WANG Lin-lin

(School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)

Fixed-wing dual-spin projectile is a class of trajectory correction projectile, of which the forward course correction fuze (CCF) and aft body can rotate at different spin rates during flight. According to its aerodynamic asymmetry characteristics, the dynamic model of fixed-wing dual-spin projectiles is derived. Nonhomogeneous angular motion equations are calculated by simplifying the model. The angular motion characteristics and stability of fixed-wing dual-spin projectiles are studied based on the angular motion equations. The results show that, when the roll rate of the CCF is constant, the angular motion characteristics of projectile are greatly affected by both the roll rate and rolling direction, and an unreasonable roll rate may cause the instability of angular motion because of the resonance; when the spin angle of the CCF stays at any angular position, the projectile has the course correction ability which is proportional to the installation angle of the canard wings. Ultimately the stability criterion of fixed-wing dual-spin projectiles is studied.

ordnance science and technology; fixed-wing dual-spin projectile; course correction fuze; nonhomogeneous angular motion equation; course correction ability; stability criterion

2014-11-14

国家自然科学基金项目(61350010)

许诺(1986—)， 男， 博士研究生。 E-mail: promise_moon@126.com；

于剑桥(1972—)， 男， 教授， 博士生导师。 E-mail: jianqiao@bit.edu.cn

TJ410

A

1000-1093(2015)04-0602-08

10.3969/j.issn.1000-1093.2015.04.005