温度对约束阻尼板振动性能影响分析
2015-11-11陈亚谢天宇海军装备部驻上海地区军事代表局江苏无锡214000
陈亚,谢天宇(海军装备部驻上海地区军事代表局,江苏无锡214000)
温度对约束阻尼板振动性能影响分析
陈亚,谢天宇
(海军装备部驻上海地区军事代表局,江苏无锡214000)
摘要:基于复模量本构关系,推导各向同性约束阻尼板的动力学控制方程,求出了四边简支约束阻尼板的固有频率以及损耗因子的解析解,与利用有限元方法数值计算结果进行了对比验证。根据粘弹性材料特性曲线,插入取样温度点,分析不同温度下约束阻尼结构的减振性能,与数值结果进行了对比验证。结果表明,存在最佳温度,使约束阻尼结构减振效果最好。
关键词:减振;约束阻尼板;有限元法
约束阻尼结构是飞机和舰船主要的舱体隔振结构之一,在减振领域应用广泛。温度对约束阻尼板的减振性能影响明显,但有关温度对约束阻尼板振动特性影响的研究较少。
约束阻尼是在夹芯板出现曲挠时,通过在阻尼层产生剪切力来消耗能量的[1-3]。因为阻尼层位于层合板中间位置,故环境适应性较强,并且减振效果较自由阻尼更加突出。粘弹性材料的弹性模量和阻尼损耗因子随温度变化,不易确定其物理、机械参数。研究中往往把动态多变的参数作为常数处理[4],但在实际工程中,约束阻尼板的减振性能受环境温度影响明显,因而考虑温度因素可以更加精确的分析约束阻尼结构的振动特性。本文从粘弹性材料特性曲线出发,考虑弹性模量和阻尼损耗因子随温度的变化[5],研究不同温度条件下,约束阻尼结构的振动特性。
1 问题描述
约束阻尼板由上下表层板和各向同性阻尼芯层板构成,见图1。

图1 约束阻尼板Fig.1 Constrained damping plate
分析夹层板自由振动问题,其基本假设为:表层刚度较大,其变形采用Kirchhoff假设[6],芯材变形采用Mindlin假设[7];各层之间理想粘结,界面无滑移;忽略厚度方向的变形,振动弯曲函数与z无关;材料层合板的密度为常数,与铺层角度无关;芯材粘弹性采用复模量模型表征[8]。
标志粘弹性材料物理机械性能的指标复弹性模量G′(G′=E′+iE″,E′为实弹性模量,E″为虚弹性模量)和阻尼损耗因子β(β=E′/E″)值,随温度而有很大的变化。
不同温度下,材料性能存在明显不同的3个区域。第1个区域是低温区,称玻璃态区。第2个区域时玻璃态区和高弹态区的过渡区,称为玻璃态转变区。第3个区域是高温区,称高弹态区。图2是某阻尼材料的特征曲线,图中弹性模量和阻尼损耗因子随温度变化剧烈,处在玻璃态转变区。[9]
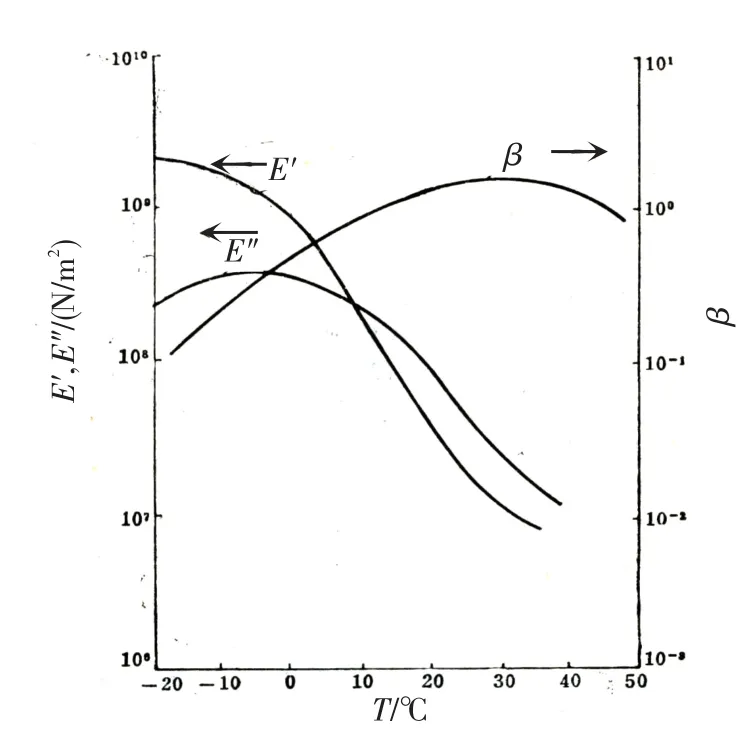
图2 某材料特性曲线Fig.2 Material propertfunction
2 约束阻尼板动力学控制方程
2.1表层和芯材位移场
如图1所示,上下表层位移:
ì
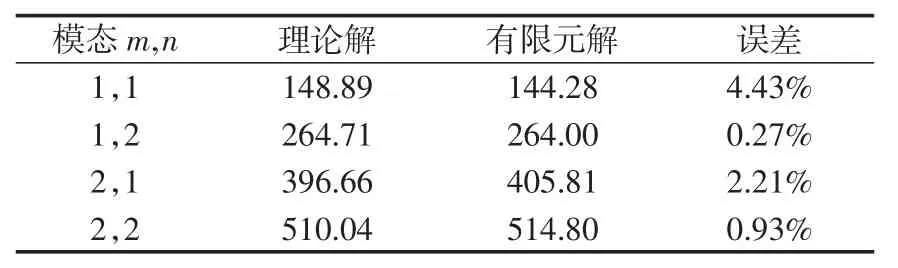
ïu(k)=u(0k)-z ∂∂whh
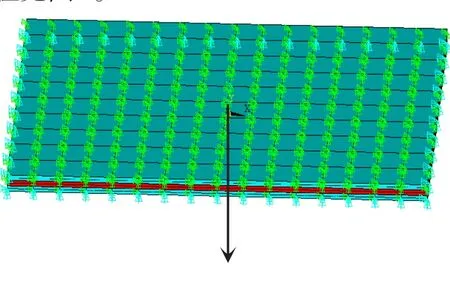
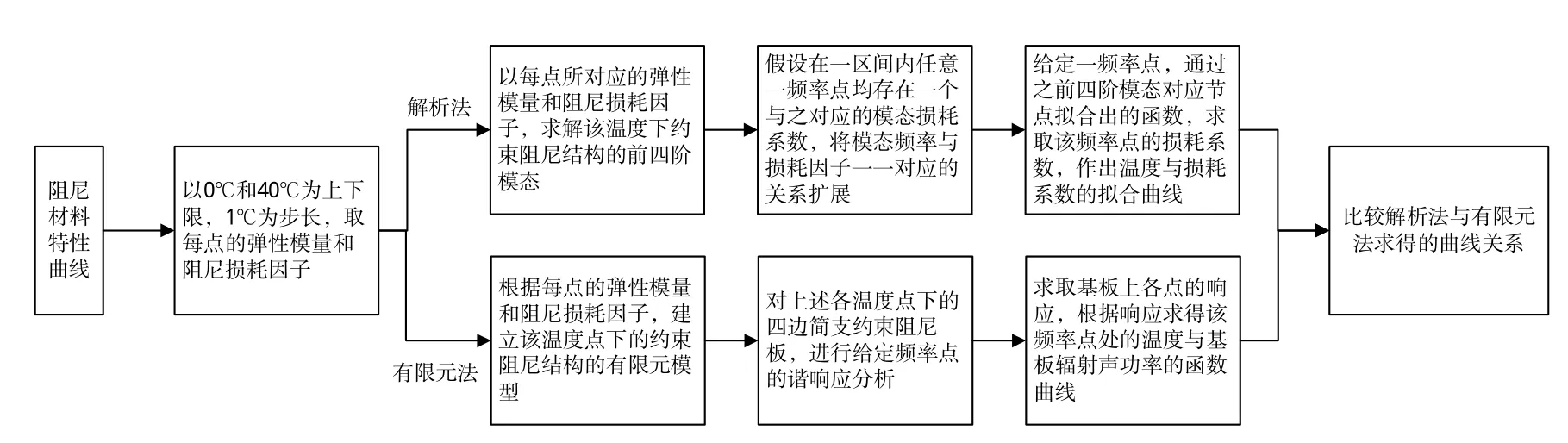
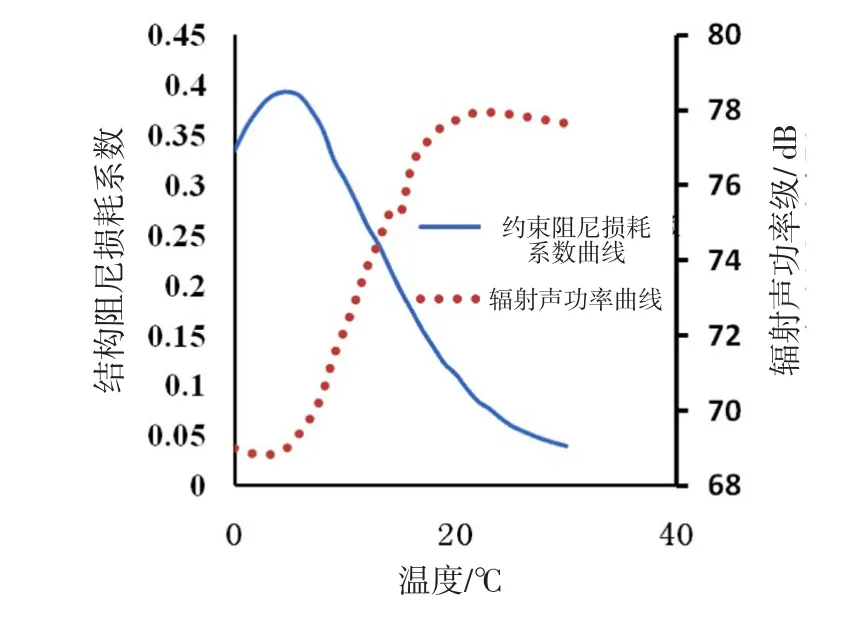
í,-k ï îv(k)=v(0k)-z ∂ ∂w 22式(1)中,坐标z为以各层中面为原点的轴向坐标。 阻尼层位移: 各层板横向位移:式(1)~(4)中:h1、h2、h3分别为上表层、阻尼层、下表层的厚度;α、β是阻尼层在z平面和z平面的附加剪切角;广义位移u、v、w、α、β是、的函数;下标1、2、3分别表示基层、阻尼层和约束层,如图1所示。 2.2阻尼层复模量本构关系 阻尼层采用复模量本构关系,各个方向的应力分量被表示为:式中, 2.3动力学控制方程 列出上下表层和阻尼层的弹性变形能和动能所有项。由于阻尼芯材面内的转动惯性相对轴向影响较小,可以忽略;同时,上下表层面内振动位移较轴向振动位移小很多,其惯性项也可忽略。 根据变分原理中的欧拉公式,得到控制方程: 式(6)中,盖板应力及阻尼层剪切力为: 采用Navier解进行求解: 将微分方程组简为矩阵形式的特性方程:式(9)中:M为质量矩阵;(K+iC)为复刚度矩阵;K、C为系数矩阵;=(U1,V1,U3,V3,W)T。 板的圆频率和阻尼损耗因子按下式计算: 2.4模型验证 采用0.6 m×0.41 m的四边简支约束阻尼结构,基板和约束层厚度均为0.006 33 m,弹性模量211 GPa,柏松比0.3,密度7 830kg/m3,阻尼层厚度0.012 66 m,弹性模量6.1×107Pa,密度1 000kg/m3。 整个约束阻尼结构外围处在空气介质中,基板的四条边界分别施加简支约束,约束层、阻尼层和基层各层之间用胶粘方式进行连接。 分别通过解析法和有限元法计算得到约束阻尼板固有频率如表1所示,两者最大误差<5%。表1中:m表示长边半波数;n表示宽边半波数。 表1 简支约束阻尼结构固有频率Tab.1 Nature frequencies for the simplsupported constrained damping plate 表1 简支约束阻尼结构固有频率Tab.1 Nature frequencies for the simplsupported constrained damping plate 模态m,n 1,1 1,2 2,1 2,2理论解148.89 264.71 396.66 510.04有限元解144.28 264.00 405.81 514.80误差4.43% 0.27% 2.21% 0.93% 由表1可以看出,当处理频率小于510 Hz的薄约束阻尼板时,实际情况基本符合第1节所进行的基本假设,故使用基于复模量和一维剪切理论的解析方法求解其固有频率较为精确。 从粘弹性材料的特性曲线出发,考虑温度对阻尼层弹性模量和损耗因子的影响,通过计算取样温度处约束阻尼结构的振动特性,统计约束阻尼结构振动特性随温度的变化关系。 3.1基本假设 1)相同温度下,阻尼层弹性模量、模态损耗因子在固有频率点到材料特性曲线测定频率点的区间内基本不变; 2)约束阻尼结构在模态频率点到测定点这一区间内存在函数关系。函数的自变量是频率,因变量是结构损耗系数,而结构损耗系数在共振频率点上的值等于约束阻尼板的阻尼损耗因子。 3.2计算过程 根据如图2所示的阻尼材料特征曲线,确定特征频率,划定温度分析区间,在这一区间内按等分原则插入一定数量的温度取样点。 解析法:分析约束阻尼板在温度取样点处的固有频率和结构损耗因子;然后将此温度取样点处,固有频率和结构阻尼损耗因子理解成自变量与因变量的关系,并扩展到全频段;利用函数拟合的方法计算出此特征频率下的结构阻尼损耗系数。依次类推,建立此频率下结构损耗系数与温度的函数曲线。 数值法:根据各温度取样点处阻尼材料的弹性模量和阻尼损耗因子,利用有限元软件建立不同温度点处约束阻尼板的分析模型,对约束阻尼板施加对称载荷,进行特征频率下的谐振分析,将所求结果导入到声学软件中求取此温度下基板的辐射声功率;以此类推,建立面平均振速与温度的函数关系。 最后,比较利用数值方法得到的辐射声功率随温度的变化曲线和之前利用解析法得到的结构阻尼损耗系数随温度变化曲线。有限元分析示意图见图3,整个流程见图4。 图3 有限元模型Fig.3 Finite element model 图4 分析流程图Fig.4 Flow chart of analsis 其中,数值计算模型中激励力施加在约束板中心、方向垂直面板向下,大小为4.448 2 N。特征频率为500 Hz。分析过程中,有限元的建模和分析基于软件ANSS完成,声学分析基于软件SSNOISE完成。 3.3结果分析 通过解析法计算得到结构阻尼损耗系数随温度变化的曲线和通过数值方法计算得到辐射声功率随温度的变化曲线,其结果如图5所示。约束阻尼板的辐射声功率随温度增加首先降低,与之相对应的是,约束阻尼结构的阻尼损耗系数随温度的升高而不断增加,约束阻尼结构耗能随之增大,减振降噪效果提高。随着辐射声功率随温度的升高而降低到4℃附近时,开始逐渐增大,而约束阻尼结构损耗系数在增加到4℃附近时,逐渐降低,约束阻尼结构耗能减少,减振效果减弱。由此可见,利用数值法计算得到的辐射声功率随温度的变化曲线与利用解析法计算得到的约束阻尼结构损耗系数随温度的变化曲线相互对应,求解得到的约束阻尼板振动特性随温度的变化曲线,计算结果真实可信。 图5 500 Hz处,结构阻尼损耗系数和辐射声功率随温度的变化曲线Fig.5 Curve of structure damping loss factor and output power with temperature in 500 Hz 本文基于复模量本构关系模型导出了约束阻尼结构的运动学微分方程。首先,给出了四边简支约束阻尼板的固有频率和阻尼损耗因子的解析解,并对其适用范围进行了讨论。然后,探究了温度对约束阻尼板声振特性的影响。分析结果显示:四边简支约束阻尼结构在受垂直于面板的对称激励时,面平均振速随温度的变化曲线与结构阻尼损耗系数随温度的变化曲线相互对应,结果可信。 参考文献: [1]王旌生,吴有生.考虑芯层横向变形的粘弹性复合材料夹层板结构的声振特性分析[J].振动与冲击,2006,25 (5):6-9. WANG JINGSHENG,WUOUSHENG. VIB- acoustic analsis of viscoelastic composite sandwich plates with transverseldeformable core[J]. Journal of Vibration and Shock,2006,25(5):6-9.(in Chinese) [2]LIN R C,LIANG Z,SOONG T,et al. An eperimental studon seismic behavior of viscoelasticalldamped structure[J]. Materials Science and Engineering,1991,13 (1):75-84. [3]KASAI K,MUSHI J,LAI M,et al. Viscoelastic damper hsteretic model:theor,eperiment and application[J]. Proceedings of ATC-17-1 on Seismic Isolation,EnergDissipation and Active Control,1993,2(2):521-532. [4]GREIF R. A Combined theoretical eperimental approach to dnamic characterization of viscoelastic materials[J]. Journal of Engineering Material and Technolog1992,114(1):77-80. [5]RIVIERE A. Analsis of the low frequencdamping observed at medium and high temperatures[J]. Materials Science and Engineering A,2004(370):204-208. [7]MINDLIN R. Influence of rotarinertia and shear in fleural motion of isotropic,elastic plates,transactions of the american societof mechanical engineers[J]. Journal of Applied Mechanics,1951(18):31-38. [9]戴德沛.阻尼减震降噪技术[M].西安:西安交通大学出版社,1986:41-50. DAI DEPEI. Damping and noise reduction technolog[M].i’an:i’an Jiaotong UniversitPress,1986:41-50.(in Chinese) [10]曹丽丽.分布式粘弹性材料本构模型的理论及应用[D].济南:山东大学,2012:17-19. CAO LILI. Studon the theorand applications of distributed constitutive models of viscoelastie materials[D]. Jinan:Shandong Universit,2012:17-19.(in Chinese) 作者简介:陈亚(1978-),男,工程师,大学。 基金项目:部委技术研究基金资助项目([2012]533-6) 收稿日期:2014-10-20; DOI:10.7682/j.issn.1673-1522.2015.02.009 文章编号:1673-1522(2015)02-0139-04 文献标志码:A 中图分类号:V279 修回日期:2015-01-12




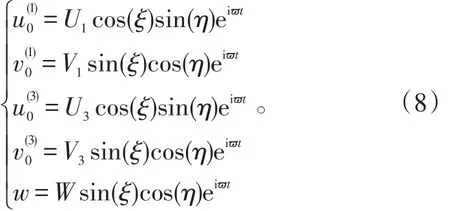

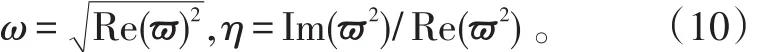
3 温度对约束阻尼板振动特性的影响
4 结论
