旋翼翼型动态失速模型参数识别及应用

柳　泉，胡国才，雷卫东（海军航空工程学院飞行器工程系，山东烟台264001）



旋翼翼型动态失速模型参数识别及应用

柳泉，胡国才，雷卫东
（海军航空工程学院飞行器工程系，山东烟台264001）

摘要：为了拓展Leishman-Beddoes（L-B）动态失速模型的应用范围，以适应特定翼型的动态失速分析，在详细分析L-B动态失速模型特点的基础上，提出一种模型参数的识别方法。以SC-1095翼型为例，采用其静态升阻特性数据，对L-B动态失速模型中的参数进行了识别，并据此对该翼型的动态失速升阻特性进行了数值计算，计算结果与试验值吻合良好。

关键词：旋翼；翼型；动态失速；参数识别

动态失速是指在直升机旋翼旋转过程中，旋翼剖面翼型迎角呈现非定常变化，当迎角超过临界值时，翼型升力系数并不与静态失速模型描述的一样直接发生失速，而是产生失速延迟的现象。这一现象多发生于直升机大速度前飞和高桨盘载荷情况下，对直升机的飞行性能和旋翼载荷具有较大的影响[1]。因此，建立准确的动态失速模型对于直升机平衡特性计算及旋翼载荷计算等方面具有重要意义。

虽然目前用CFD方法可以模拟翼型的动态失速特性[2]，但是该方法计算量大并且将其计算结果用于直升机气动载荷计算还有很大的困难。而Leishman-Beddoes半经验动态失速模型因其方法简单直观，涉及的经验参数少，适于时域求解，被广泛应用于直升机旋翼的气动载荷计算[3]。该模型最初由Beddoes[4-5]在20世纪70年代中期发展起来，随后，Leishman[6-7]对其进行了拓展，使其完整地模拟翼型动态失速过程。文献[7]对需识别的参数及方法进行了简单介绍。

文献[8-10]只是针对给定翼型数据进行了动态失速过程仿真，并没有开展相关参数识别工作。

本文对SC-1095翼型的L-B动态失速模型中所需要的参数进行识别，为某型直升机的气动特性计算打下基础。

1　L-B动态失速模型

1.1附着流

1.1.1法向力系数

环量法向力系数的递推公式为：式（1）中：CNα为法向力系数随迎角变化曲线斜率，可通过翼型静态失速试验得到；αn为迎角；αEn为有效迎角；n、n分别为缺损函数，式（2）、（3）中：A1、A2、B1、B2为给定经验参数，A1=0.3、A2=0.7、B1=0.14、B2=0.53；为Prandtl-Glauert压缩性修正因子，Ma为马赫数；Δαn为样本时间间隔Δt=tn-tn-1内的迎角变化量；ΔS为样本时间间隔内的时间参数变量，式（4）中：V为翼型剖面速度；c为翼型弦长。非环量法向力系数的递推公式为式（5）中：T=c，a为音速；

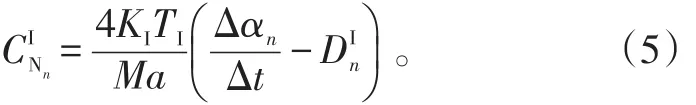
Ia为缺损函数，

迎角变化率引起的法向力系数的递推公式为：式（8）中：Δq为迎角变距率，；Δ为样本

n时间间隔内迎角变化率的变化量；Dqn为缺损函数，

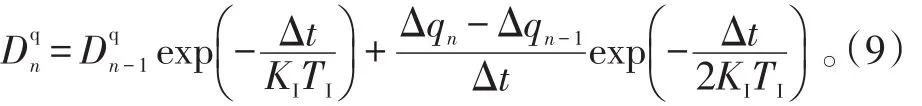
附着流情况下总的法向力系数为

1.1.2俯仰力矩系数

非环量法向力系数引起的1/4弦线处俯仰力矩系数为

迎角变化率引起的1/4弦线处俯仰力矩系数为

式（13）中：

DqMn为缺损函数，

附着流情况下总的俯仰力矩系数为

1.1.3弦向力系数

附着流情况下的弦向力系数为

1.2前缘分离

翼型出现气流前缘分离的条件是动态失速模型的关键。气流发生前缘分离与前缘压力密切相关，而前缘压力又与法向力系数CN有关，所以将法向力系数是否大于气流前缘分离的临界法向力系数CN1作为气流前缘分离的判断依据，CN1可通过翼型静态失速试验得到。

非定常情况下，法向力系数CN的变化滞后于迎角的变化，而前缘压力的变化又滞后于法向力系数的变化，所以须对法向力系数进行一阶滞后补偿处理，引入一个法向力系数替代值C′N，用于表征前缘压力的变化，式（17）中为缺损函数，式（18）中，Tp为与马赫数有关的经验参数。

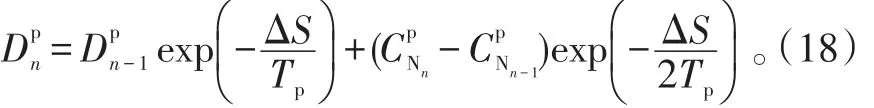
于是，C′N>CN1为非定常情况下气流发生前缘分离的条件。

1.3后缘分离

准定常情况下，由Kirchhoff理论可得后缘分离时翼型的法向力系数为式中，f为后缘分离点，通过翼型静态失速试验可得其与迎角的关系为式（20）中：α0.7为f=0.7时的迎角，通过试验发现[11]大部分翼型静态失速临界迎角处f≈0.7；S1、S2可通过翼型静态失速试验得到。

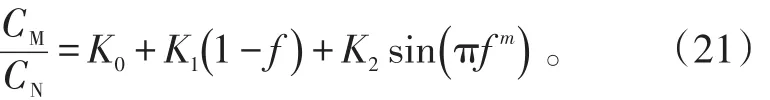
俯仰力矩系数经验公式为式（21）中：K0、K1、K2为与马赫数有关的经验参数；经验参数m=2。

弦向力系数为式中，η为修正因子，η=0.95。

非定常情况下，由于翼型压力分布和附面层响应与分离点之间存在相位差，需对分离点位置进行修正。

定义修正迎角：

该迎角用于确定修正的分离点f′，考虑到附面层响应的滞后影响，对其进行一阶滞后补偿处理，最终的后缘分离点为：式中，为缺损函数，式（25）中，Tf为与马赫数有关的经验参数。

后缘分离情况下，非定常法向力系数、俯仰力矩系数和弦向力系数分别为：

1.4动态失速

动态失速的整个发展过程可描述为：

1）当C′N>CN1时，前缘气流发生分离，此时计无量纲时间τv=0；

2）前缘涡脱离翼型上表面形成脱体涡向翼型后缘传播，在此过程中，τ以无量纲时间步长开始

v累加，当τv=Tvl时，脱体涡到达翼型后缘，Tvl为与马赫数有关的经验参数；

3）脱体涡离开后缘一个弦长，τv继续累加，当τv=2Tvl时，视为整个过程结束。

在τv=0~Tvl过程中，涡诱导升力的变量等于非定常环量升力与Kirchhoff理论近似得到的非定常升力之差，即

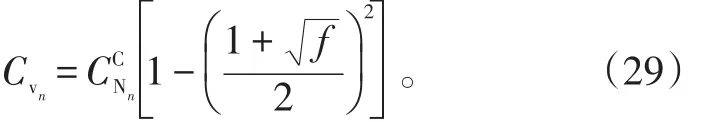
积累的涡诱导升力的递推公式为：式中，Tv为与马赫数有关的经验参数。

在τv=Tvl~2Tvl过程中，Cvn=0。

因此，总的法向力系数为

翼型上的压力中心随涡的运动而改变，其表达式为

由于压力中心变化引起的翼型俯仰力矩系数的变量为因此，总的俯仰力矩系数为在动态失速过程中，即C′N>CN1时，弦向力系数为式中，Df为与马赫数有关的经验参数。

由翼型法向力系数与弦向力系数可得翼型总的升阻系数分别为：

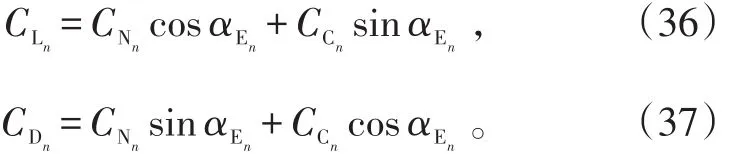
2　参数识别

通过对L-B动态失速模型的分析研究，可知需通过翼型静态失速升阻曲线识别的参数为：CNα

、CN1

、

α0.7、S1、S2。

本文所采用的静态升阻曲线取自参考文献[12]，以Ma=0.3时为例，升阻曲线如图1、2所示。

由翼型法向力系数与升阻系数的关系可得：

图1　升力系数随迎角变化曲线Fig.1 Lift coefficient vs angle of attack

图2　阻力系数随迎角变化曲线Fig.2 Drag coefficient vs angle of attack

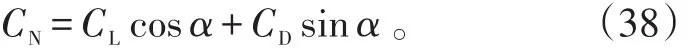
翼型法向力系数与迎角关系曲线如图3所示。由图3可得：CNα

=0.107、CN1

=1.228 1、α0.7=12°。

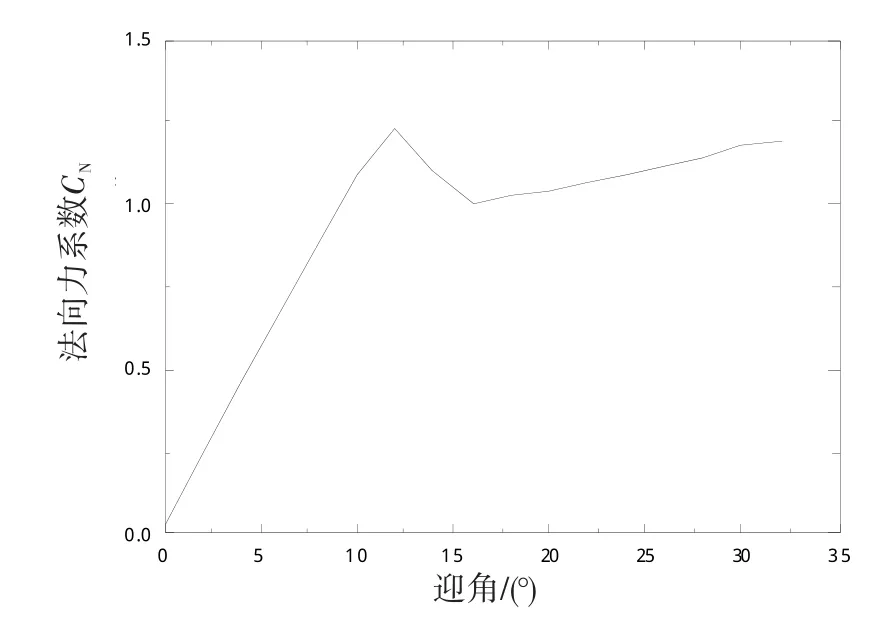
图3　法向力系数随迎角变化曲线Fig.3 Normal force coefficient vs angle of attack

由式（19）可求得α<α0.7、α>α0.7时所对应的分离点f1、f2，再将所得分离点及对应迎角分别代入式（20）求得S1、S2。

至此，所需参数识别完毕。

3　模型验证

为验证模型及所识别参数的正确性，采用以下算例进行验证计算，模型中所有给定经验参数及试验值取自文献[6]，给定经验参数如表1所示。

算例：翼型SC1095，c=0.1，Ma=0.3，

从图4~6可以看出：通过本文所建模型及所识别的参数进行计算得到的升力系数、阻力系数和俯仰力矩系数与文献值吻合较好，验证了本文模型及参数识别方法的正确性。从图4可以看出：动态失速模型计算得到的升力系数与静态失速试验值相比，产生了失速延迟。

表1　经验参数Tab.1 Eperiential coefficients

表1　经验参数Tab.1 Eperiential coefficients

参数K0K1 K2 Df Tp Tf TvTvIMa 0.3 0.0025 -0.135 0.04 8.0 1.7 3.0 6.0 7.0 0.4 0.006 -0.135 0.05 7.75 1.8 2.5 6.0 9.0 0.5 0.02 -0.125 0.04 6.2 2.0 2.2 6.0 9.0 0.6 0.038 -0.12 0.04 6.0 2.5 2.0 6.0 9.0 0.7 0.030 -0.09 0.15 5.9 3.0 2.0 6.0 9.0 0.75 0.001 -0.13 -0.02 5.5 3.3 2.0 6.0 9.0 0.8 -0.01 0.02 -0.01 4.0 4.3 2.0 4.0 9.0

图4　升力系数随迎角变化曲线Fig.4 Lift coefficient vs angle of attack

图5　阻力系数随迎角变化曲线Fig.5 Drag coefficient vs angle of attack

图6　俯仰力矩系数随迎角变化曲线Fig.6 Pitching moment coefficient vs angle of attack

4　结论

根据SC1095翼型的静态失速升阻曲线，对L-B动态失速模型中所需参数进行了识别，并利用识别参数对该翼型的动态失速升阻特性进行了数值计算，计算结果与试验值吻合良好。

参考文献：

[1]陈文轩. CFD法中的动态失速模拟[J].直升机技术，2008（3）：55-68. CHEN WENUAN. Dnamic stall predictions bCFD method[J]. Helicopter Technique，2008（3）：55- 68.（in Chinese）

[2]LEISHMAN J G. Principles of helicopter aerodnamics [M]. 2nd ed. Cambridge UniversitPress，2007：525-526.

[3]王浩文，高正.采用综合气弹分析方法的旋翼非定常气动载荷计算[J].南京航空航天大学学报，2003，35（3）：268-272. WANG HAOWEN，GAO ZHENG. Unsteadrotor airload prediction using a comprehensive areoelastic analsis [J]. Journal of Nanjing Universitof Aeronautics &Astronautics，2003，35（3）：268-272.（in Chinese）

[4]BEDDOES T S. A snthesis of unsteadaerodnamic effects including stall hsteresis[J]. Vertica，1976，1（2）：113-123.

[5]BEDDOES T S. Representation of airfoil behavior[J]. Vertica，1983，7（2）：183-197.

[6]LEISHMAN J G，BEDDOES T S. A generalized model for unsteadaerodnamic behavior and dnamic stall using indicial method[C]//42nd Annual Forum of the American Helicopter Societ. Washington D.C.，1986：243-264.

[7]LEISHMAN J G，BEDDOES T S. A semi-empirical model for dnamic stall[C]//42th Annual Forum of the American Helicopter Societ. Washington D.C.，1986：3-17.

[8]宋辰瑶，徐国华.旋翼翼型非定常动态失速响应的计算[J].空气动力学学报，2007，25（4）：461-467. SONG CHENAO，U GUOHUA. Computation of unsteaddnamic stall response on rotor airfoils[J]. Acta Aerodnamic Sinica，2007，25（4）：461-467.（in Chinese）

[9]刘雄，张宪民，陈严，等.基于Beddoes-leishman动态失速模型的水平轴风力机动态气动载荷计算方法[J].太阳能学报，2008，29（12）：1449-1455. LIUIONG，ZHANGIANMIN，CHENAN，et al. Transient aerodnamic load prediction of horizontal ais wind turbine based on the Beddoes- leishman model[J]. Acta Energiae Solaris Sinica，2008，29（12）：1449-1455. （in Chinese）

[10]刘铮.动态失速对直升机空中共振的影响分析[D].南京：南京航空航天大学，2013. LIU ZHENG. Investigation of the influence of dnamic stall on helicopter air resonance stabilit[D]. Nanjing：Nanjing Universitof Aeronautics and Astronautics，2013.（in Chinese）

[11]LEISHMAN J G，CROUSE G L. State-space model for unsteadairfoil behavior and dnamic stall[C]//30th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dnamics and Materials Conference. Mobile，1989：1372-1383.

[12]HOWLETT J J. UH-60A black hawk engineering simulation program，NASA-CR-166309[R]. Washington D.C.：NASA，1981：5.1-52-5.1-54.

Parameter Identification and Applicatioonn of Rotor Airfoil Dnamic Stall Model

LIU Quan, HU Guo-cai, LEI Wei-dong
（Department of Airborne Vehicle Engineering, NAAU,antai Shandong 264001, China）

Abstrraacctt:: On the basis of the characteristics of Leishman-Beddoes (L-B) dnamic stall model, the method of parameters identification was put forward in order to epand the application range of L-B dnamic stall model and adapt to dnamic stall analsis of specific airfoil. The dnamic stall lift and drag were calculated with the parameters identified from the stat⁃ic stall lift and drag curves of SC-1095, the results agreed well with the eperimental value.

作者简介：柳泉（1986-），男，博士生；胡国才（1964-），男，教授，博士，博导。

基金项目：航空科学基金资助项目（20145784010）

收稿日期：2014-11-26；

DOI:10.7682/j.issn.1673-1522.2015.02.007

文章编号：1673-1522（2015）02-0129-05

文献标志码：A

中图分类号：V212.4

修回日期：2015-01-05