高中物理试题中数学思想研究

戚亚军

摘要：通过对物理试题的学习，人们学到了很多物理方面的知识，更重要的是在学习中，留下了很多科学的方法。大部分的有作为的物理科学家所取得的重大成就和所采用的科学方法是相互协调的。所以，在物理教学中，教师不能够只教给学生物理知识，更要对他们进行学习方法的点拨。

关键词：高中物理 试题研究 思想

一、目前高中物理教学中数学方法的教学存在的问题

在高中的学习中，很多学生都将物理试题和数学学科，放在了首要的地位，因为这两门课程，在学习中，相对较难，可以说，这两门课学好了，其他的科目都很容易。在学生当中，总是将这两门课分开来看待，学生学习了很多关于函数、图像、对数的计算，指数的计算，以及一些极值的计算，还有圆、椭圆等的知识，可以运用这些知识来解答数学中的相关习题，但是，在利用这些知识能解决物理问题的时候，却总是表现出不会，根本不知道怎么使用;还有的学生，会运用数学知识，也是胡乱将数学公式带入到了物理计算题中，不懂得知识之间如何进行迁移、使用，分析出现的这些原因，主要是老师在教学中，没有将物理公式解释清楚，同时数学老师也没有将数学公式进行能力的提升，应该在讲课的时候，将数学方法迁移到物理的相关题型中，这样，学生就会由熟悉到熟练，逐步培养数学思想。

还有的教师在课上遇到关于物理习题中，蕴含着数学的思维的时候，总是一带而过，简单提一下，这是运用的数学的某某计算公式，至于怎么带入，那是数学方面应该解决的问题，你们不会，那是数学没有学好，不会的下去问数学老师。面对这种情况，学生对于遇到的蕴含数学思想的物理题目，依然是听的一知半解，没有深刻的掌握，课后又将之抛之脑后，做别的习题去了。因此，这些方面的问题都要引起重视，只有这样，数学的思想方法才能被运用到物理试题当中，让学生正确认识他们之间的联系，培养他们学习的积极性和主动探索的能力。

二、数学思想在物理问题中的渗透

（一）数学思想

通常所说的数学思想主要是依据现代世界的空间形式和数量之间的关系，对于人的意识之间的影响，通过人的大脑进行思维后，产生的一种结果性的物质，在不断的认识活动中，形成具有普遍规律的方法。建立数学用数学解决问题的思想。运用这些思想，比如方程函数思想，数形结合的思想等，来解答物理中的问题。

（二）相互之间的渗透

数学思想方法具有很强的概括性，抽象的概念经过数学思想方法，可以化繁为简，形成熟练的运用过的程度，这不是一天就能完成的，需要长时间的积累，逐步渗透才可以实现，这就需要教师在教学的过程中，慢慢将数学思想方法进行渗透，教师可以利用现实生活中的实景，进行指导，给学生建立一个生活化的教学，让学生对这门课感兴趣，接受物理概念及相关的现象，适时指导学生利用数学思维方法，进行对物理情景中的数学建模，或者是在物理模型中建立数学方法。

三、具体应用实例

在具体的物理试题的计算中，我们往往利用数学方法进行解答，不只是解决物理问题，更重要的是为了得到一种利用数学思维解答物理问题。采用数学的思维去将问题转化，建立数学模型，运用数学方法进行解答，而后，再通过物理问题的方法去验证结果，最终获得问题的答案。

（一）物理试题中的数学函数模型的建立

数学函数模型，目的是建立一种未知量和已经量之间的关系，通过函数的方法建立一个方程，运用数学方法求解，这样对于物理试题的解决，能够快速解决问题。

例1：十字路口一辆汽车在红灯亮后，停车等待，当绿灯亮后，它以加速度为3m/s2的速度开始行驶，此时，正好有一辆自行车从远处行驶过来，以6m/s的速度行驶，问汽车从路口开始行驶，需要多长时间，两车的最远距离是多少？

解答：倘若汽车开始行驶了一段时间为t，此时，汽车移动了：s1=at2的距离，自行车移动的距离为：s2=vt，他们之间的间距是：Δs=s2-s1=vt-at2。将已经有的数据进行带入，从而能够建立Δs与t之间的函数关系式：△s=-（t-2）+6。

根据这个式子可以知道，当t=2s时，Δs最大的数值是6m。

（二）物理试题中数学不等式模型的建立

一般来说，建立数学不等式模型，就是要依据题目中的要求来建立，通过所给的已知条件和未知条件，建立一个不等式的关系式，从而通过对不等式的求解，最后得出问题的答案。

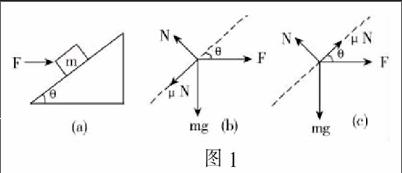
例2：根据图1所示，用一个推力F推动质量为m的物体，物体放在倾斜角为θ的一个斜面上，已知斜面对物体的最大静摩擦力为它们接触面间压力的μ倍，求水平力F的大小？

图1

对解答过程进行分析：当该物体正好要向上滑动的时候，受力分析如图1（b）中所示，再对物体下滑的时候，也进行受力分析，见图1（c）中所示，从图中可以看出，不管物体是向上滑动，还是向下滑动，物体同斜面之间的压力都是N=mgcosθ+Fsinθ。

如果想要让物体不向上滑动，可以建立关系式：Fcosθmgsinθ+μN。

如果想要物理不向下滑动，可以建立关系式：Fcosθ+μNmgsinθ。对这两个式子进行解答，可以得到F的取值范围为：

mg≥F≥mg

综上所述，在物理的试题中，建立数学模型，可以对题目进行巧妙地解答，构建物理试题中的数学模型，显示出数学思维的实用性和重要性，所以，在今后的物理教学中，或者是化学教学中，要不断培养学生这两门课程之间的思维互换，不断拓展学生的物理思维和数学模型的建立，对相关的问题进行解答，提高自己的学习能力和科学方法。

参考文献：

[1]周鹏.“问题生成”教学模式——基于问题为中心的高中物理课研究[J].湖南中学物理，2012（12）.

[2]张开洋.新课标下高中物理教学模式探究[J].教师，2012（34）.

[3]田伶新.高中物理教学模式的研究[J]. 新课程研究：下旬刊，2012（10）

[4]关燕.高中物理教学中运用原始问题培养学生科学探究能力的实践研究[D].西北师范大学，2010

[5]项华阳.“动手做”在初中物理教学中的实践研究[D].上海师范大学，2009.

（责编 张景贤）