曲轴连杆轴颈圆度加工过程的转速优化

2015-11-09李庆涛张校通李纪强

机械工程师 2015年3期

李庆涛，张校通，李纪强

（1.吉林烟草工业有限责任公司，吉林延吉133001；2.东北大学机械工程与自动化学院，沈阳110819；3.95905部队机务大队，辽宁锦州121018）

0 引言

曲轴是发动机的关键零部件之一，其加工内容主要包含三个方面，主轴轴颈的加工、连杆轴颈的加工以及曲轴偏心拐的加工，其中曲轴连杆轴颈的粗加工与半精加工多采用车削或铣削来实现［1-3］。两种工艺相比较而言，铣削工艺的应用更普遍，这主要是由于曲轴连杆轴颈车削加工工艺较为复杂且需要两道工序才能完成，而铣削加工速度高，特别是双刀盘数控外铣工艺，其加工质量稳定，加工效率较高［4-6］。双刀盘外铣是利用两个快速旋转铣刀盘的横向进给实现铣削的，铣削时要求曲轴进行周向转动，双刀盘曲轴铣床机床如图1所示。伺服电机旋转通过滚珠丝杠的驱动，使铣刀盘在水平面上实现横向进给，在铣刀盘进给的时候需要两个减速箱以及滑台同时移动，由于在进行曲轴连杆轴颈的圆度加工时，铣刀盘需要作变速运动，这就对伺服电机的控制以及驱动功率提出了挑战。本文从分析曲轴与铣刀盘运动关系着手，以舒缓铣刀盘进给突变，提高曲轴加工效率为目的，对曲轴连杆轴颈加工过程进行了优化。

图1 双刀盘曲轴铣床结构图

1 曲轴连杆轴颈圆度加工过程分析

图2为铣刀盘在进行曲轴连杆轴颈圆度加工的示意图，表达了铣刀盘与曲轴连杆轴的运动关系，当铣刀盘靠近曲轴连杆轴颈时，由于铣刀盘自身在快速旋转，同时铣刀盘对曲轴连杆轴颈有一定的切深，通过曲轴转角与铣刀盘的横向进给，完成曲轴连杆轴颈的圆度加工［7］。

图2 曲轴连杆轴颈圆度加工示意图

对于双刀盘外铣加工而言，其铣削过程可细分为三个阶段：插入切削、软接近切削以及旋转切削，并且以旋转切削为主。由于此三种切削加工方式比较难界定，并且没有特定的路径，因此本文仅对曲轴转角与铣刀盘的运动关系做详细分析。

对于曲轴连杆的圆度加工，曲轴与铣刀盘之间的运动关系可以看作曲柄滑块机构，如图3所示，图中，L为曲轴轴心与曲轴连杆轴心之间的距离，Q为铣刀盘轴心与曲轴连杆轴心之间的距离，H为铣刀盘轴心与曲轴轴心之间的垂直高度差，y为铣刀盘轴心与曲轴轴心之间的水平距离，θ为曲轴的旋转角位移。若要通过控制铣刀盘的进给来配合曲轴转动完成曲轴连杆轴颈的圆度铣削加工，就必须求出曲轴在任意旋转角度时，所对应的铣刀盘的进给量（位移），也就是要有y与θ的函数关系。通过对图3的分析可建立出如下公式［8］：

图2 曲轴连杆轴颈圆度加工模型简化图

式中：R为铣刀盘的半径；r为曲轴连杆轴颈的半径。

2 曲轴与铣刀盘运动学分析

2.1 曲轴与铣刀盘运动关系

将式(3)进行简化，可得到

式（4）是关于铣刀盘的进给加速度A、曲轴旋转角位移θ、曲轴转动的角速度Vθ以及曲轴转动的角加速度αθ的函数表达式，在已知后三项的前提下，可以求解铣刀盘的进给加速度A。另外当曲轴匀速转动时，即曲轴转动的角加速度αθ为零，此时铣刀盘进给加速度A与曲轴转动的角速度V20成正比例关系。

2.2 曲轴与铣刀盘系统的Adams分析

在进行曲轴连杆轴颈加工时，曲轴与铣刀盘之间的运动关系可近似地看作曲柄滑块机构，其中曲轴的连杆就类似曲柄滑块机构中的曲柄，而铣刀盘则类似于曲柄滑块机构中的连杆和滑块，因为铣刀盘兼有旋转和移动功能。图4则是曲轴和铣刀盘系统在Adams中的运动关系简化图。

图4 曲轴及铣刀盘系统运动关系简化图

图4 中AB段曲柄代表曲轴的连杆，其长度L=150 mm，为连杆轴心与曲轴轴心之间的距离；BC段连杆代表铣刀盘，其中表示铣刀盘轴心到连杆轴心的距离；另外铣刀盘中心轴和曲轴轴心有一高度差H=65 mm。为了直观地了解曲轴转动的角位移θ，曲轴转动角速度Vθ，对铣刀盘移动加速度A的影响，对曲轴进行了多组转速加载，加载速度 Va分别为 10°/s、8°/s、6°/s 和 4°/s，经Adams仿真，得到了在不同曲轴转速下曲轴转角θ与铣刀盘进给加速度的关系，其结果如图5所示。

图5表明，铣刀盘进给的加速度随曲轴转速提高而增大。同时在曲轴转角θm=120°时，铣刀盘的加速度A出现一次峰值，当曲轴转角到达θn≈0°位置时，铣刀盘的加速度A出现一次谷值。以曲轴转速Vθ=10°/s为例，在一个加工圆周内，铣刀盘加速度的峰、谷值分别为Amax=3.77mm/s2和Amin=-6.26 mm/s2，并且绝大部分时间内铣刀盘移动的加速度值都在峰值以内，仅有约23%的时间大于此峰值。对于曲轴轴颈圆度加工而言，如果伺服电机选择时其功率能保证铣刀盘移动时的峰值加速值，这时我们必须为了约23%的加工时间降低曲轴转速，实为可惜，为此提出了曲轴的变速转动方法，仅在单周期内进行一次加减速的变换，这样既能保证铣刀盘的加速度在峰值满足要求，也能保证铣刀盘的加速度在谷值时满足要求（峰值附近采用了降速处理），此方案在一定程度上提高了曲轴转动的平均角速度，即提高了加工效率。

图5 曲轴转速与铣刀盘加速度关系图

3 曲轴转速优化

经上述分析可知，当曲轴匀速转动时，铣刀盘的加速度谷值与峰值的大小之比为1.66，为此我们假定曲轴旋转时的两个基本速度有如下关系：

式中：V1为曲轴转动的最低速度，也是加速阶段的起始速度和减速阶段的终止速度；V2为曲轴转动的最高速度，也是加速阶段的终止速度和减速阶段的起始速度。

3.1 曲轴转速加速过程分析

曲轴与铣刀盘运动学分析表明，在已知曲轴转速、曲轴转角以及曲轴转动的角加速度的前提下，可通过式（3）求解铣刀盘的加速度，反之也可在已知铣刀盘加速度的前提下，求解曲轴的角加速度。假设曲轴的旋转的角加速度都能通过改变驱动功率来实现，建立了加速阶段的运动方程：

式中：Ax为铣刀盘的最大允许加速度；θn为铣刀盘加速度处于谷值时曲轴的转角；θm加铣刀盘加速度处于峰值时曲轴的转角；α为曲轴角加速度；V1为加速起始速度；V2为加速终止速度；θ1为曲轴加速起始角度；θ2为曲轴加速终止角度；T1为曲轴加速阶段旋转半周所用时间。

以铣刀盘允许的最大加速度Ax=3.77 mm/s2为例，应用Matlab软件进行计算优化，获得了加速阶段主要运动参数之间的关系，如图6所示。

通过优化分析可知，当加速的起始角度θ1=23°，曲轴的角加速度α=0.375°/s时，曲轴连杆的轴颈圆度铣削加工耗时最短T1=19.34 s，且此条件下终止角θ2=76.24°恰好满足假定条件（半周期内完成加速）。

3.2 对曲轴减速过程曲轴转速的优化

参照曲轴加速阶段的运动方程，建立了曲轴减速阶段的运动方程：

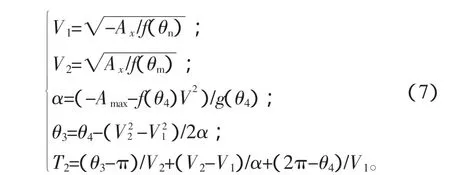
式中：Ax为铣刀盘的最大允许加速度；θn为铣刀盘加速度处于谷值时曲轴的转角；θm为铣刀盘加速度处于峰值时曲轴的转角；α为曲轴角加速度；V1为减速终止速度；V2为减速起始速度；θ3为曲轴减速起始角度；θ4为曲轴减速终止角度；T2为曲轴减速旋转半周所用时间。

图6 加速阶段各运动参数之间关系

图7是减速阶段各运动参数之间的关系，同样减速阶段也假定在曲轴转动半周内完成。

图7 减速阶段各运动参数之间关系

通过优化分析可知，当减速的终止角度θ4=349°，曲轴的角加速度α=-0.244 8°/s2时，曲轴连杆的轴颈圆度铣削加工耗时最短T1=18.97 s，且此条件下减速起始角θ3=267.4°。

3.3 优化结果校验

将Matlab优化的结果，进一步计算得到加速减速阶段的时间节点，并将曲轴在各个时间段内的运动参数加载到分析模型的曲柄上，经Adams仿真分析，获得了优化后的铣刀盘移动加速度与曲轴转角之间的关系，结果如图8所示。

其加速过程中的铣刀盘加速度最小值为Amin=-3.764 mm/s2，减速过中的铣刀盘加速度最小值为Amin=-3.7742 mm/s2，仿真终止角度 θ=359.94°，由于选取的加速起始点和减速终止点都是整数值，如加速阶段的加速起始角θ1=23°和减速阶段的减速终止角θ4=349°，以及在计算结果取值方面都可能存在一定的误差，但仿真结果与理论值比较接近，在可接受范围之内，因此可认为优化过程是正确的。