某航空活塞发动机曲轴振动模态分析

冯世榕

（中国民用航空飞行学院，四川 广汉 618307）

0 引言

某固定翼飞机装用美制水平对置、空气冷却、自然吸气、4汽缸航空活塞发动机，其曲轴为非全支撑式结构，由4个与连杆相连的曲柄和3个与机匣相连的曲颈组成，前端直接与螺旋桨相连，没有减速机构。曲轴与连杆、活塞和飞重等部件组成的曲轴轴系，是发动机振动的主要来源，也是导致发动机性能恶化、齿轮损伤、座舱噪声增大等故障的主要原因，研究曲轴轴系振动特性［1-6］，有助于降低部附件损伤和提高发动机可靠性，对确保飞行安全有主要意义。

1 曲轴轴系振动的分析方法

本文拟采用模态分析理论和成熟的有限元分析软件，对曲轴轴系的振动特性进行分析。将曲轴轴系视为多自由度系统，根据振动分析理论，可得到轴系微分方程的表达式［7-9］为

式中：［M］为质量矩阵；｛x｝、｛x˙｝、｛x¨｝为节点位移、速度和加速度；［C］为阻尼矩阵；［K］为刚度矩阵；［f（t）］为在节点上作用的外载荷向量。

由于运动中产生的阻尼对曲轴轴系固有频率影响小，所以将其可以忽略。因此，可以通过求解结构无阻尼自由振动方程来获得结构的固有特性。线性无阻尼振动系统的振动微分方程为

首先考虑自由振动，即｛f（t）｝=0，式（2）变为

自由振动是由一系列简谐振动叠加而成，因此可以将式（3）分解为

求解方程（6），可得n阶固有圆频率ωr及对应的n阶模态振型｛φ｝r（r=1，2……N）。将N阶振型按照某种标准归一化（通常是对质量进行归一化，对质量归一化获得的模态称为正则模态）后，按各阶顺序排列，便可得到模态矩阵｛φ｝。进行坐标变换，令｛x｝=｛φ｝｛q｝，方程（2）两边同时左乘｛φ｝T，方程（2）变为

利用模态对刚度和质量的正交性，即

式（7）可变为以下形式：

式中：Mr=｛φ｝Tr［M］｛φ｝r为第 r阶模态质量；Kr=｛φ｝Tr［K］｛φ｝r为第 r阶模态刚度；Fr=｛φ｝Tr｛f｝为第 r阶模态力；qr为第r阶模态质量。

式（9）即为模态方程，相当于n个“单自由度”的运动微分方程，即

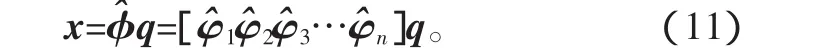
将式（11）代入式（2），用和前面相同的处理步骤，得到的n个“单自由度”运动微分方程为

设式（2）所表示系统的初始条件为 x（0）=x00）=。由式（11）知，可以将模态坐标q的初始条件用q0表示，则

最后，式（2）系统的物理坐标解根据式（11）定义的变换得到，为

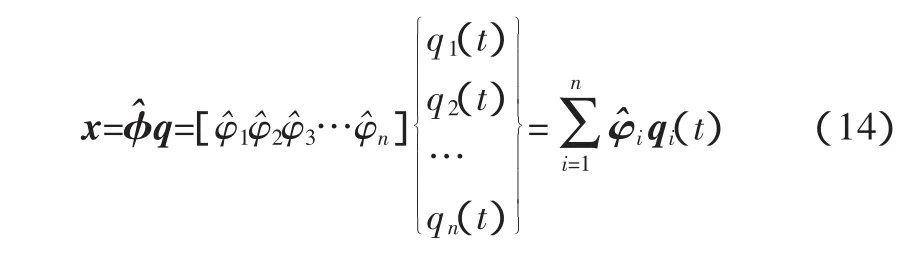
式（14）被称为模态叠加定理，是计算模态分析的理论基础。它表明n自由度系统的物理坐标响应，可由系统本身物理特性所决定的n个模态，通过n个“权系数”叠加得到，这n个“权系数”由系统的初始条件和外界激励确定。

2 曲轴振动模态分析

2.1 曲轴三维实体模型

本文研究的曲轴由曲颈、曲柄、凸肩和螺旋桨连接法兰盘等几部分组成，各部件的结合处都有倒角，以避免出现应力集中，导致曲轴断裂的故障。曲轴上还有不少滑油通道和喷射孔，部分表面不规则，因此在实际计算时进行了一些简化处理。

2.2 建立计算模型

螺旋桨通过一段截面为六边形的轴段与法兰盘刚性连接，为了更好模拟实际情况，建立计算模型时，在法兰盘与螺旋桨之间拉伸了一段六边形的轴，该段轴的与法兰盘刚性连接，同样使用shell 181单元进行表面网格划分，然后使用solid 10node 187单元进行体化分，但该段轴的材料与曲轴材料不同，曲轴材料特性：弹性模量E=2.09×1011Pa，泊松比 μ=0.3，密度 ρ=7.809×103kg/m3；连接轴段材料特性：E=0.7×1011Pa，μ=0.3，ρ=3.305×103kg/m3，这样在将螺旋桨以集中质量加在曲轴上时，需要减去连接轴段的质量和转动惯量，减去连接轴段质量和转动惯量后螺旋桨的数据见表1。

表1 减去连接轴段的螺旋桨的质量和惯性矩

通过分析，认为对曲轴轴系进行模态分析时的网格划分要求不高，故采用solid 187单元，四面体网格，首先使用shell 181单元对表面进行网格划分，用面控制体，然后进行体的自由划分，体化分成功后，需将已经进行网格划分的表面删除，如图1所示。

2.3 自由模态分析

在ANSYS中进行计算模态分析时，由于自由模态分析前5阶是6个方向自由度的零频率刚体模态，对于曲轴轴系的扭振研究没有意义，本文也仅列出前5阶频率，见图2和表2。

图1 曲轴实体网格划分结果

图2 二阶扭转振动模拟计算

表2 轴系固有频率值

2.4 加载状态下的模态分析

实际工作中，曲轴轴系中各受力部件所处的边界条件与自由状态不一样，特别是活塞、连杆等高速运动部件的等效质量与重量完全不同，必须对这些部件的等效转动惯量进行计算。

等效转动惯量的计算公式为

在自由模态计算的基础上更改用于模拟活塞连杆组的质量单元的输入参数并对曲颈施加载荷之后，便可进行加载状态下的模态计算。得到曲轴轴系前5阶固有频率，见表3。

表3 轴系固有频率值

3 结论

将进行试验测试数据与模拟计算结果的对比分析，见表4。

表4 模拟计算与实际测试对比分析

从对比的数据可以看出，一阶扭振误差大于5%，其余均小于5%。造成误差的原因主要有以下几个：1）建模时，省略了工艺倒角和润滑油孔；连杆轴颈是空心的，实际上空心孔的轴线与连杆轴线并不重合，但在建模时按重合处理了；2）使用Pro/E计算各部件转动惯量时，输入的密度值均是估算的；部分部件的转动惯量使用经验公式计算，而经验公式本身就存有一定的误差；3）计算所得各阶扭振振型并非完全是扭转振动，是各类振动耦合后的结果，只不过是扭振在其中占主导地位而已。

［1］ 吴炎庭，袁卫平.内燃机噪声振动与控制［M］.北京：机械工业出版社，2005：239-240.

［2］ 张德文.从约束试验数据提取自由结构模态参数［J］.强度与环境，2005，32（1）：10-15.

［3］ 吕兴才，舒歌群，沈红斌.汽车发动机曲轴纵向振动的研究［J］.汽车工程，2001，23（5）：332-336.

［4］ 梁兴雨，舒歌群，张宝欢,等.基于瑞利法的内燃机曲轴纵向振动研究［J］.中国机械工程，2008，19（6）：648-652.

［5］ 王长荣，谭达明.内燃机动力学［M］.北京：中国铁道出社，1990.

［6］ 李震，桂长林，孙军.内燃机曲轴轴系振动分析研究的现状、讨论与展望［J］.内燃机学报，2002，20（5）：469-474.

［7］ 管迪华.模态分析技术［M］.北京：清华大学出版社，1996：45-46.

［8］ Heylen W，Lammens S，Sas P.Modal Analysis Theory and Testing［M］.Levven:Katholieke Universiteit Levven-Department werktvi gkunde，1997.

［9］ 李人宪.有限元法基础［M］.北京：国防工业出版社，2010：3.