基于Hilbert-Huang变换的FSK信号降噪识别

文捷

（河北医科大学第二医院，河北　石家庄　050000）

基于Hilbert-Huang变换的FSK信号降噪识别

文捷

（河北医科大学第二医院，河北石家庄050000）

Hilbert-Huang变换（HHT）相对于经典的FFT变化，对信号的频率定义做了创造性的改进，HHT理论上能精确给出信号中频率随时间变化的规律，在此基础上，涌现了许多新型信号处理方法。文章对Hilbert-Huang变换进行了理论分析，在此基础上提出了一种基于HHT的FSK信号降噪识别方法，通过运用奇异值分解降噪和HHT边际谱算法，在抑制噪声的同时，突显了FSK信号特征，达到了良好的降噪识别效果。

HHTFSK降噪

1　引言

Hilbert-Huang变换是N.E.Huang等人在1998年提出来的一种新的信号处理方法，简称HHT［1］。这是第一次对傅里叶变换的基本信号和频率的定义做的创造性的改进，HHT中不再认为组成信号的基本成分是正弦信号，而是一种称为内在模式函数（IMF）的信号，也就是满足以下2个条件的信号：①整个信号中，零点数和极点数相等或至多相差1；②信号上任意一点，由局部极大值点确定的包络线和局部极小值点确定的包络线的均值为0，即信号关于时间轴局部对称。HHT包含两大部分：第一部分为经验模式分解（EMD），用于将信号分解成有限个IMF分量；第二部分就是对每个IMF分量进行Hilbert变换，得到瞬时频率和瞬时幅度，从而得到时频平面上的能量分布谱图，而不同于傅里叶变换分析中的全局频率和能量。这是一种以瞬时频率为核心概念的方法［2］，理论上能精确给出信号中频率随时间变化的规律，避免了虚假频率等冗余现象，同时EMD的基随信号自适应地产生，不同信号的基是唯一的，不需要选择。

2　EMD算法

在傅里叶变换分析中，信号分解的方法是傅里叶变换，在HHT中则采用经验模式分解（EMD）方法，其算法步骤介绍如下：

定稿日期：2015-06-12

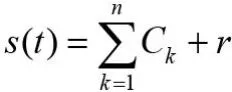
3　边际谱

对上述得到的每个IMF分量进行Hilbert变换，求每个IMF分量的解析信号：

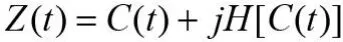
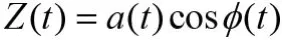
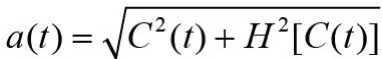
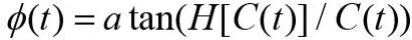
可得到IMF分量的瞬时频率：

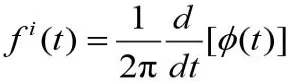
可得信号的每个IMF分量的Hilbert为：

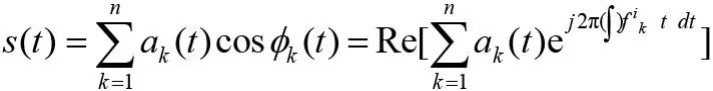
这时记信号的Hilbert谱为：

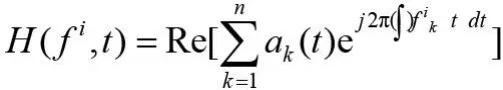
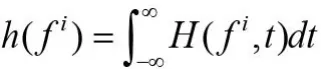
从上式可以看出，信号的边际谱在某个瞬时频率处的能量大小，正是信号Hilbert谱在这个瞬时频率处所有时间上的加权和，真实的反应了信号在该瞬时频率处的存在性。

4　基于HHT的降噪

假设接收到的信号是原始信号加白噪声，为：

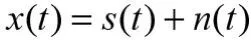
构造信号的自相关矩阵R，由于噪声的存在，所以自相关矩阵R是非奇异的。对矩阵R进行特征值分解，可以得到k个不增序排列的特征值，特征值的个数与自相关矩阵的维数有关。一般而言，在这些特征值中，只有前面若干个具有比较大的值，其余值较小，这些比较大的特征值对应着原始信号中的特征成分，而那些比较小的特征值则对应着信号中的噪声成分［5］。

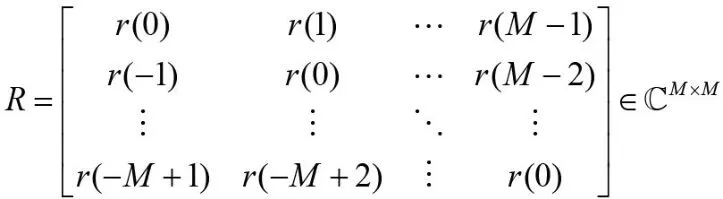
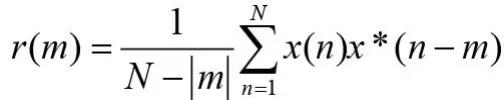
对矩阵R进行特征值分解，可得：

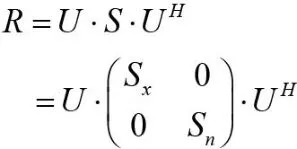
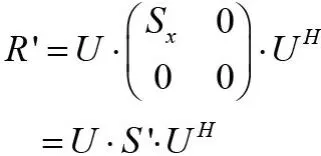
可以发现：

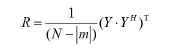
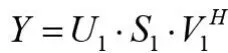
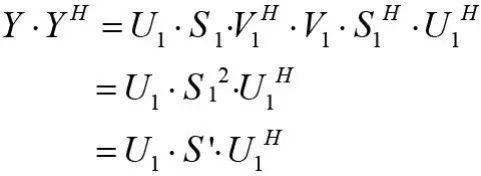
另一方面，对延时矩阵进行奇异值分解，去除噪声子空间后，对信号的重构也是很方便的。可以发现，延时矩阵中每行元素都是信号的延时排列，所以找到相同的信号元素，算出其平均值，就可以完成信号序列的重构。

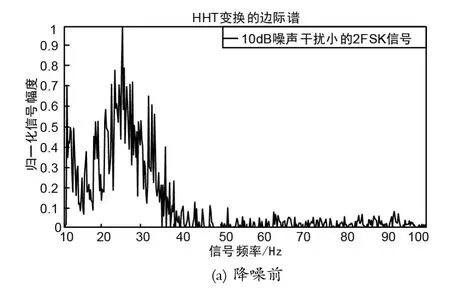
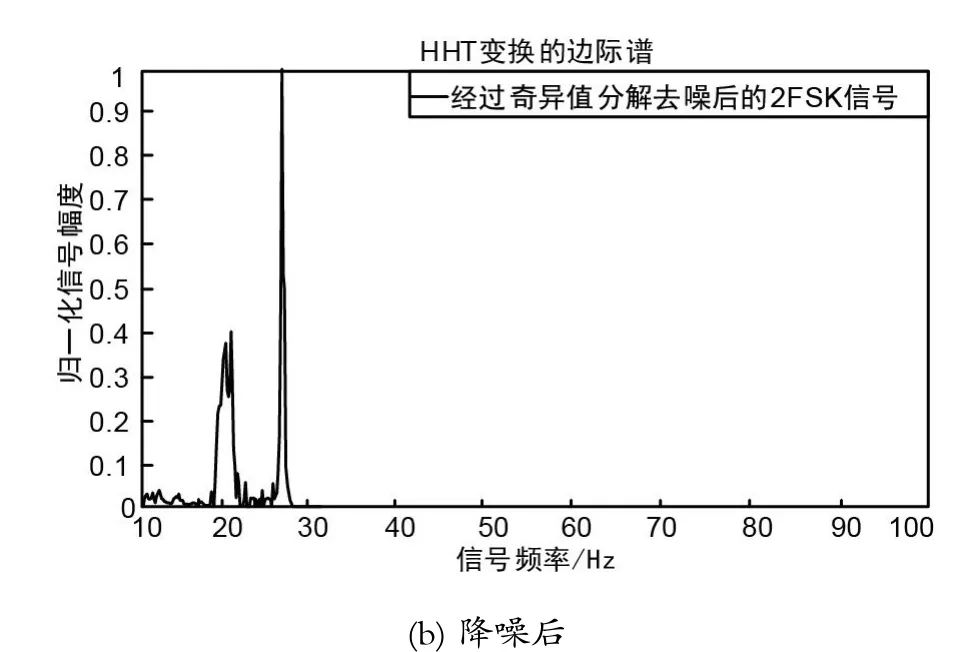
图1　基于奇异值分解2FSK信号边际谱

选取2FSK经过Hilbert-Huang变换，码元速率，采样速率，载波频率，载波频差，信号持续时间，信噪比,对2FSK信号运用HHT变换，降噪前后信号的边际谱如图1所示。

从图1可以看出，经过奇异值分解降噪后的HHT边际谱有了明显的改善，进而可以很准确的识别出信号的调制类型以及完成信号的参数估计。

5　结束语

针对FSK信号的特点，分析了FSK信号Hilbert-Huang变换（HHT）的Hilbert谱和边际谱特征，针对HHT变换对信号的采样率要求比较高并容易受到噪声影响的特点，采用奇异值分解去噪的方法可以去除信号的噪声，获得了良好的信号降噪处理效果。

［1］Huang N.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis［C］//Proc R Soc Lond,1998,454（A）：903-995.

［2］Huang N,Wu M L,Qu W D,et al.Applications of Hilbert-Huang Transform to Non-Stat ionary Financial Time Series Analysis［J］.Applied Stochastic Models in Business and Industry,2003,361（19）：245-268.

［3］Qiu L.Fundamental Frequency Determinati on based on Instantaneous Frequency Estimation［J］.Signal Processing, 1995,44（2）：233-241.

［4］Erden M F，Kutay M A.Repeated filtering in consecutive fractional Fourier domains and its application to signal restoration［J］.IEEE Trans Signal Processing，1999，47（5）：1458-1462.

［5］Boll S.Suppression of Acoustic Noise in Speech Using Spectral Subtraction［J］.IEEE Transactions on Acoustics,Speech,and Signal Processing,1979（2）：113-120.

［6］胡谋法,董文娟,王书宏，等.奇异值分解带通滤波背景抑制和去噪［J］.电子学报，2008，36（1）：111-116.

FSK Signal Noise Reduction and Recognition Based on HHT

WEN Jie
（The Second Hospital of Hebei Medical University,Shijiazhuang Hebei 050000,China）

Compared with classical FFT,Hilbert-Huang Transformation（HHT）has a creative improvement on the definition of signal frequency.HHT gives the precise description of variation rules of frequency with time,based on which many signal processing methods are proposed.This paper theoretically studies the application of HHT,and provides a HHT based FSK signal recognition and noise reduction method.This method can suppress the noise and amplify the FSK features by using singular value decomposition and marginal spectrum algorithms,and achieve favorable noise reduction and signal recognition effects.

HHT；FSK；noise reduction

TP393

A

1008-1739（2015）13-52-4