关于岭参数k的选取问题
2015-11-08张拓卜晓明陈奕含杨忻怡杨璐
张拓,卜晓明,陈奕含,杨忻怡,杨璐
(渤海大学数理学院,辽宁锦州121013)
关于岭参数k的选取问题
张拓,卜晓明,陈奕含,杨忻怡,杨璐
(渤海大学数理学院,辽宁锦州121013)
对岭估计中参数k的选取问题进行了研究,并对Hoerl-Kennard公式进行了改进,使参数k的选取更为准确。
岭估计;参数;均方误差;有偏估计
岭回归估计是应用最广泛的一种有偏估计,其目的在于减小均方误差,所以岭参数k的选取也应使MSE(β^(k))达到最小。k的选取不仅依赖于未知参数β和σ2,而且这种依赖关系也没有明确确定,这都使k的选取存在很大难度[1]。目前关于k的选取方法已有10余种,主要方法包括岭迹法、方差扩大因子法、双H公式法、Hoerl-Kennard公式法等。本文在已有文献基础之上,主要对Hoerl-Kennard公式[2-3]进行研究与改进,以期获得更小误差。
1 岭估计
考虑线性回归模型

参数β的岭估计定义为β^(k)=(X'X+kI)-1X'Y,其中:当k>0时,称k为岭参数或偏参数;当k=0时,β^(0)=(X'X)-1X'y为β的LS估计[4]。
为方便讨论,本研究采取典则形式。
定义设X'X的特征值为λ1,λ2,…,λp,对应的标准正交化特征向量为φ1,φ2,…,φp,记Φ=(φ1,φ2,…,φp),Φ为p×p标准正交阵,即Φ'Φ=Ι。记Δ=diag(λ1,λ2,…,λp),则X'X=ΦΔΦ',线性模型:
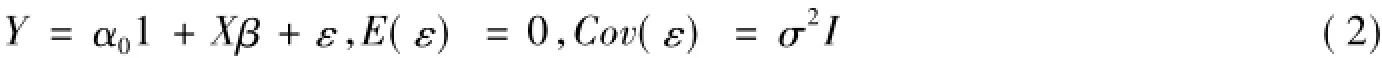
可写为

其中Z=XΦ,α=Φ'β。称式(3)为线性回归模型的典则形式,α为典则回归系数。均方误差在参数与估计的正交变换下保持不变,故典则回归系数和原回归系数拥有相同的均方误差[5],即MSE(^α(k))=MSE(β^(k))。
2 Hoerl-Kennard公式的进一步改进
由前文及文献[1,6]可以得到:
引理1令H(k)=MSE(^α(k)),则H(k)=MSE(β^(k)),有

其中:k≥0;H(k)为光滑函数。又H'(0)<0,H'(+∞)>0,故使H(k)取得最小值的k必然存在。记k0=inf{ k:H'(k)=0},则H(k0)<H(0),α^(k0)改进了LS估计α^(0)。
引理2存在使H'(k0)=0,其中按升序排列[7],且记α(i)=
将λ1,λ2,…,λp中与α(i)相对应的值记为λ(i),i=1,2,…,p,Hoerl-Kennard公式给出的k值估计恰好为。当α的各分量α均相等,即
定理1如果存在2≤r≤p,且α(r-1)<α(r),则存在k0>,使
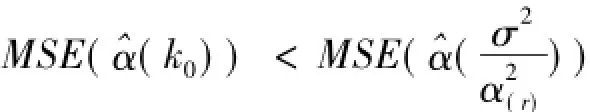
证明因为α(r-1)<α(r),所以若kα


对式(4)与(5)进行加和,则有:
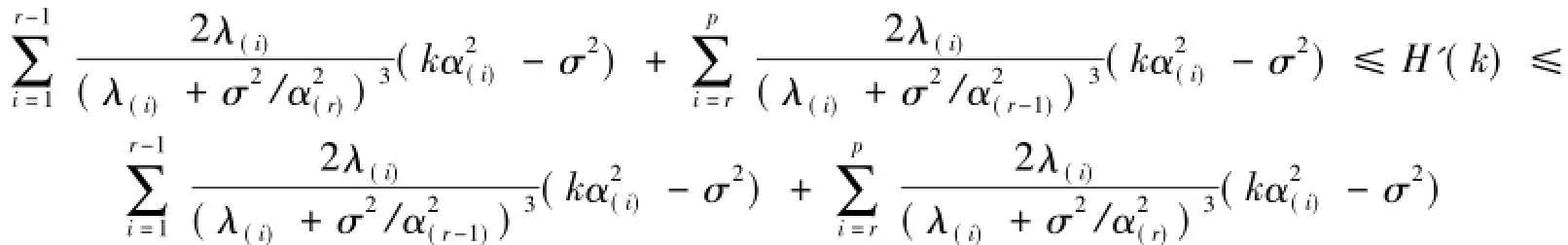

定理得证。
推论若2≤r≤p,且α(r-1)<α(r),则存在ki>k0,使MSE(ki))<MSE(k0))。时,就可以按该定理方法持续进行下去,使均方误差逐渐减少,于是可以得到更进一步的改进。当改进参数取,同样可以得到以下结论。
证明过程可以参考定理1。自此在Hoerl-Kennard公式基础上更进一步改进了关于岭参数k的选取方法,使岭参数k的选取更为准确。
[1]陈希孺,王松桂.近代回归分析[M].合肥:安徽教育出版社,1986.
[2]Hoerl A E,Kennard R W.Ridge regression:biased estimation for non-orthogonal problems[J].Technometrics,1970,12(1):55-67.
[3]Hoerl A E,Kennard R W.Ridge regression:application for non-orthogonal problems[J].Technometrics,1970,12(1):69-72.
[4]王松桂.线性模型的理论及其应用[M].合肥:安徽教育出版社,1987.
[5]Sarkar.Mean square error matrix comparison of some estimators in linear regressions with multicollinearity[J],Statistics and Probability Letters,1996,30(2):133 -138.
[6]王志福.岭估计中参数选择的一种新方法[J].锦州师范学院学报:自然科学版,2003,24(1):47-49.
[7]李明奇,吴旭.回归系数的部分岭估计[J].河南理工大学学报:自然科学版,2011,30(6):749-752.
[8]王浩华,李胜军.岭回归中参数估计的讨论[J].海南大学学报:自然科学版,2009,27(1):5-7.
(责任编辑刘舸)
Selection of Ridge Parameter k
ZHANG Tuo,BU Xiao-ming,CHEN Yi-han,YANG Xin-yi,YANG Lu
(College of Mathematics and Physics,Bohai University,Jinzhou 121013,China)
An in-depth study on choosing parameter k in ridge estimation was researched.At the same time,in order to make parameter k more accurate,we did a proper improvement on Hoerl-Kennard formula.
ridge estimation;parameter;mean square error;biased estimation
O212.2
A
1674-8425(2015)04-0136-03
10.3969/j.issn.1674-8425(z).2015.04.027
2015-01-16
国家自然科学基金资助项目(11371030)
张拓(1989—),男,硕士研究生,主要从事应用概率统计方面研究。
张拓,卜晓明,陈奕含,等.关于岭参数k的选取问题[J].重庆理工大学学报:自然科学版,2015(4):136 -138.
format:ZHANG Tuo,BU Xiao-ming,CHEN Yi-han,et al.Selection of Ridge Parameter k[J].Journal of Chongqing University of Technology:Natural Science,2015(4):136-138.
