基于粒子群算法的偏置进近航段多目标优化

辛 超 吴振亚 范 铮

基于粒子群算法的偏置进近航段多目标优化

辛 超 吴振亚 范 铮

为了提高偏置Ⅰ类精密进近飞行程序的设计精度，对其采用改进型的粒子群算法。在求解过程中对粒子群算法进行了约束改进，提出了符合本文的改进粒子群算法，能更好产生初始解，进而处理个体极值和全局极值的选取问题。根据程序设计理论对优化问题构建约束条件，建立多目标分层优化目标函数求解非支配解，最终通过某机场进行验证。

飞行程序是航空器根据飞行仪表和对障碍物保持规定的超障余度所进行的一系列预定的机动飞行，主要分为传统程序和PBN程序。在某些情况下，由于地形条件比较复杂，机场周边净空环境很差，台址问题，机场施工要求，需要将航向台偏离跑道的中心线，此时航向台的航道波束不能与跑道中心延长线一致，就要建立偏置的精密进近航段。本文依据国际民航组织文件8168的要求对偏执进近航段进行评估分析，并且在计算过程中引入粒子群算法对偏置进近航段进行多目标求解设计。应用分层优化的思想对多目标进行分层优化，产生符合条件的初始粒子建立储存非支配解和没有支配关系解的外部集，通过循环更新和拥挤距离，选择合适的全局极值进行优化。

偏置精密进近

ILS进近程序根据航空器飞行的时间顺序和高度的变化可以分为：进场航线航段、起始进近航段、中间进近航段、精密进近航段和最后复飞航段这五个航段。图1为精密进近航段的示意图，精密进近航段包括最后进近下降过程和起始复飞与中间复飞阶段。

偏置的精密进近程序是在特殊情况下，航向台的航道波束与跑道中心延长线不一致的精密进近航段。

偏置的Ⅰ类精密进近必须满足下列要求：

1. ILS航道与跑道中线延长线的夹角不超过5°；

2. 交点应在标称下滑道到达的高度至少在入口以上55m处；

3. 所有超障面和计算是基于与航向台对正的假想跑道，其长度、入口标高和入口至切入点的距离与真跑道相同，而航向道的宽度和ILS基准高也基于假想跑道入口的数据；

4. 这种程序的OCA/H不得小于切入高度/高+20m。

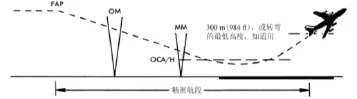
图1　精密进近航段

对比一般的精密进近，可以看出偏置Ⅰ类精密进近航段是精密进近的一种特殊情况。但如何确定具体的最后进近点的位置、偏置角度、下滑角度、决断高等参数因素需要综合考虑。

粒子群算法的多目标求解设计

粒子群算法在于每个粒子在迭代过程中跟随两个极值来调整自己的飞行姿态；一个是粒子本身的历史的最优解Pbest，另一个是整个粒子群的历史的最优解Gbest。在搜索解的过程中，每个粒子向整个群体传递信息，群体将这些信息汇总之后，进行周而复始的信息交换，使得个体经验值使得粒子能快速寻找到单个的局部最优解，通过比较单个最优解获得群体的历史最优解，从而使整个群体快速收敛。

1.群体大小 M ：M是个整型参数。通常选取M=50～200。

2.最大速度Vmax：粒子每次迭代中允许飞行的最大速度。

3.学习因子c1,c2：学习因子c1是每代粒子向前代粒子学习自身最优位置经验能力体现，学习因子c2是每代粒子向前代群体学习最优位置经验的能力体现。通常取c1=c2=2，c1,c2也可以取其他值，c1=c2，[0,4]。

4.停止准则：当迭代次数达到设定值或者解的精度达到满意度时停止算法迭代。对最优解的精度有要求，则将每一代之间差值达到某个特定数值为停止准则。

5.领域拓扑结构：全局版本粒子群优化算法将整个群体作为粒子的领域，整个群体将历史最优解作为唯一的最优解，种群中所有粒子都根据这个唯一解更新自己的位置和速度。

多目标函数分层优化

当有足够数目且满足条件的粒子时，算法将进入目标函数的适应度值的计算。通过分析可以发现，文中多目标函数太过粗糙，对算法的求解可能存在不精确问题，故将目标函数进行拆分，得到：

这四个新的目标函数，进一步明确了优化算法的最终目标是这些参数每一个在可行域范围内尽可能的小这一目标，对应到实际的飞行程序设计中代表着着陆标准最低。将这个新的多目标函数作为第一层优化的多目标，通过第一层优化，得到满足约束条件的非支配解集，在此基础上将下列函数作第二层优化的多目标函数：

通过第二层优化，得到满足约束条件的新的非支配解集，从而实现多目标的分层优化，提高了解的精度。将上述第一层的非支配解集作为第一外部集的一部分，第二层的非支配解集作为第二外部集的一部分，它们统称为外部集。第二外部集是全局极值的候选集合也是最终输出可能的求解结果。如图2为粒子数据流图。

表1　机场资料

表2　跑道物理特性

表3　最优粒子参数

图2　粒子数据流多层优化图

改进的粒子群算法

改进的粒子群算法主要通过改变参数和与其他算法融合。对参数的改进包括对惯性权值ù、学习因子c1,c2、飞行时间t等的调整。

偏置的Ⅰ类精密进近航段设计的最终反映，是通过一张带有偏置角、下滑角、决断高、复飞梯度的等参数的航图展示。根据这些参数就能反推出一个精密进近航段及其保护区，即如果知道这些参数的组合，那么对应着唯一的精密进近航段也就一目了然。将这些飞行程序设计中的基本参数组合起来，并将其构建成向量即一个9维向量粒子作为粒子群算法中的个体。根据多目标函数和约束条件进行求解，过程如下：

步骤 1设置粒子群初始参数，在随机生成M个粒子；

步骤 2 对粒子进行标记，记在可行域范围的粒子为1，其他则为0；

步骤 3评价种群中所有粒子，将当前各个粒子的位置和适应度值储存在自身的Pbest中，比较标记为1的所有Pbest中目标函数值最优的个体的位置和目标函数值，选择强非支配解Pbest存储于Gbest（当有两个以上的Pbest没有支配关系时，随机选取其中之一）；

步骤 4更新各个粒子的速度和位置，公式如下：

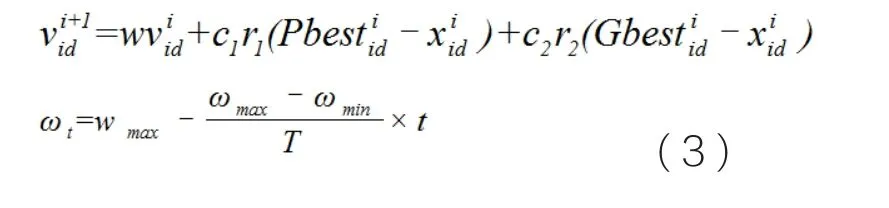
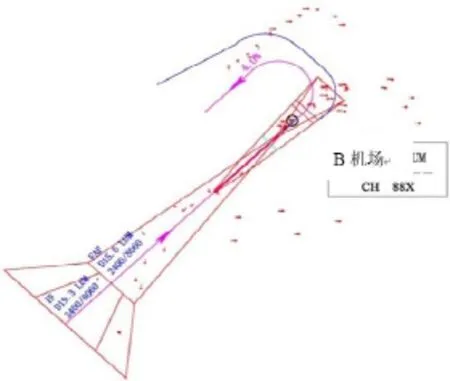
图3　可行方案图

图4　三维仿真图

步骤 5评价更新后种群中所有粒子；

步骤 6个体极值更新：比较种群中每个粒子当前目标函数值与其Pbest的目标函数值。

步骤 7全局极值更新：比较标记为1的所有Pbest和Gbest的目标函数值，当Pbest支配Gbest时，用当前Pbest更新Gbest，当两者没有支配关系时，以50％的概率进行替换。

步骤 8若满足终止准则，则输出Gbest及其目标函数值并停止算法，否则转向步骤2。

应用实例验证

B机场拟在05号跑道方向建立偏置的精密进近航段，提高跑道的起降架次，增强旅客运输能力，满足B市当地经济发展的需要。表1，表2为B机场的部分资料。

将转化后的障碍物数据依据多目标优化函数、改进的粒子群算法，计算得出下列最优粒子参数。

对可行最优粒子进行可行性分析。基于Auto CAD绘制，偏置的Ⅰ类精密进近航段及最后复飞航段的保护区。图3为最优粒子参数所对应的保护区图，依照绘制的二维保护区图，对保护区内的障碍物进行评估。

综上，本文所求的符合多目标函数和约束条件的可行最优粒子，经检查符合实际的超障要求和精密进近航段要求。图4为精密进近航段及其最后复飞航段保护区的三维仿真图像，由图像可以清晰的知道本文可行最优粒子所对应的飞行程序保护的大致走向。

结束语

对于本文所建立的多目标函数和约束条件，基于改进型的多目标粒子群算法的设计，计算得出符合某市机场周边障碍物的可行的最优粒子，即符合条件的飞行程序设计各项参数。将绘制出飞行程序的保护区图，对保护区内的障碍物进行评估，经评估可行的最优粒子对应的飞行程序设计参数满足民航国际组织8168文件的设计要求。初步设计出某机场05号方向偏置的Ⅰ类精密进近方案。

10.3969/j.issn.1001-8972.2015.21.010