30 m预应力简支箱梁受弯极限承载力仿真分析
2015-11-05庞凌志
庞凌志
(中铁四院集团广州设计院有限公司,广东广州510000)
30 m预应力简支箱梁受弯极限承载力仿真分析
庞凌志
(中铁四院集团广州设计院有限公司,广东广州510000)
由于现阶段的桥梁设计局限于运用线弹性理论,无法客观反映桥梁结构材料的非线性行为,而有限元理论可以很好地处理这类问题。现运用ANSYS有限元软件对一片30 m预应力简支箱梁进行极限承载力仿真分析,对预应力箱梁非线性行为进行了全过程跟踪分析,最终得出预应力箱梁极限承载力。
预应力;简支箱梁;钢筋混凝土;有限元;材料非线性
0 前言
预应力混凝土梁桥以其承载能力高、构件截面小、强度大、能充分利用高强材料等优点,在桥梁建设中扮演着日益重要的角色。但是在设计此类梁桥时通常沿用线弹性理论分析其内力,而以极限状态法来确定构件的承载能力、刚度和抗裂性。这种由规范提供的设计方法对常规设计也是行之有效且简单可行的,但不能反映钢筋混凝土箱梁作为闭口薄壁结构的力学特征,不能清晰地给出预应力箱梁在受到荷载作用下各阶段的形态及其发展规律,不能客观地反映钢筋混凝土材料非线性行为,从而也不能十分准确地评估整个箱梁结构的可靠度。因此,有必要对预应力混凝土梁的极限承载力进行全过程跟踪分析。本文运用ANSYS有限元软件对某高速公路上主线桥的一片30 m预应力简支箱梁进行极限承载力仿真分析。
1 预应力简支箱梁模型
某预应力简支箱梁为单箱单室结构,跨径30 m,混凝土设计标号为C50。箱梁底板上设置了2束、腹板上设置了6束,共计8束5股的钢绞线,采用后张法施工。其箱梁横截面构造如图1所示。
2 单元选取及网格划分
混凝土选用SOLID65单元,用整体式模型考虑普通钢筋的作用,按实际纵向配筋率0.6%修改SOLD65单元实常数。设置SOLID65单元的KEYOPT(7)=1,即考虑混凝土压碎时拉应力释放,以便于计算收敛。
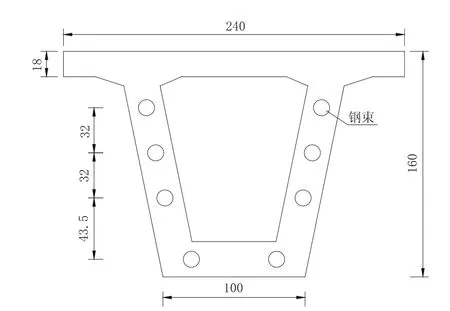
图1 30m预应力简支箱梁横截面构造图
预应力筋选用LINK8单元。由于预应力筋在箱梁内部即设置了平弯,又设置了竖弯,如果按常规的方法——使预应力筋的每个节点与混凝土的节点完全重合,这样建模过程过于复杂。对此,在该项分析中,采用约束方程法,利用CEINTF命令使混凝土的节点对预应力筋节点提供三向约束,这样在建模时不用刻意去考虑两者节点之间的重合,且单元大小也不用划分太小,利于非线性计算时收敛。
为避免在约束处出现应力集中现象,在简支梁两端设置钢垫块。钢垫块选用SOLID45单元。
有限元模型及预应力模型分别如图2、图3所示。
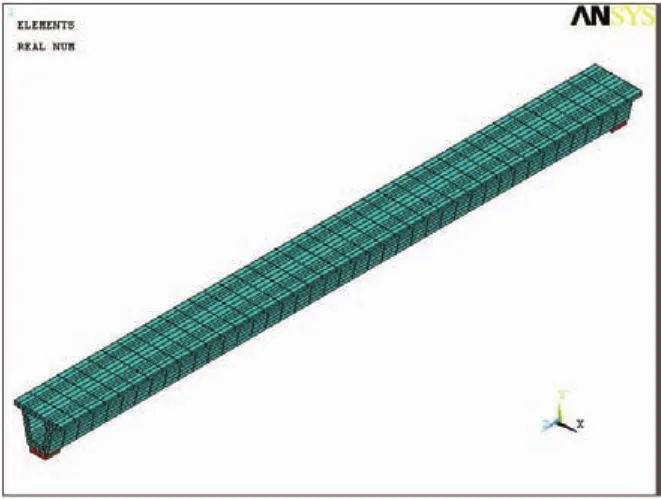
图2 30 m预应力简支箱梁有限元模型

图3 30 m预应力简支箱梁预应力筋模型
3 混凝土的本构关系及破坏准则
国内外研究人员为了准确拟和混凝土的单轴受压应力-应变试验曲线,提出多种形式的数学函数来作为混凝土的受压应力-应变曲线方程。现有的本构模型可以大致分为三大类:线弹性本构模型、非线弹性本构模型、塑性本构模型及其他力学模型。在该项分析过程中,混凝土的本构关系采用非线弹性本构模型中的过镇海建议公式:
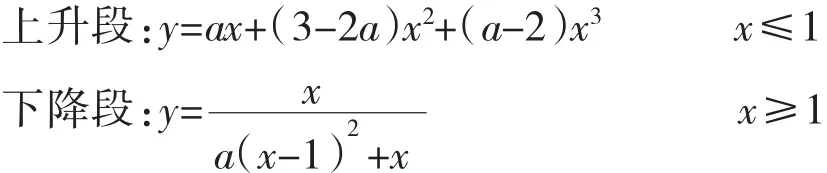
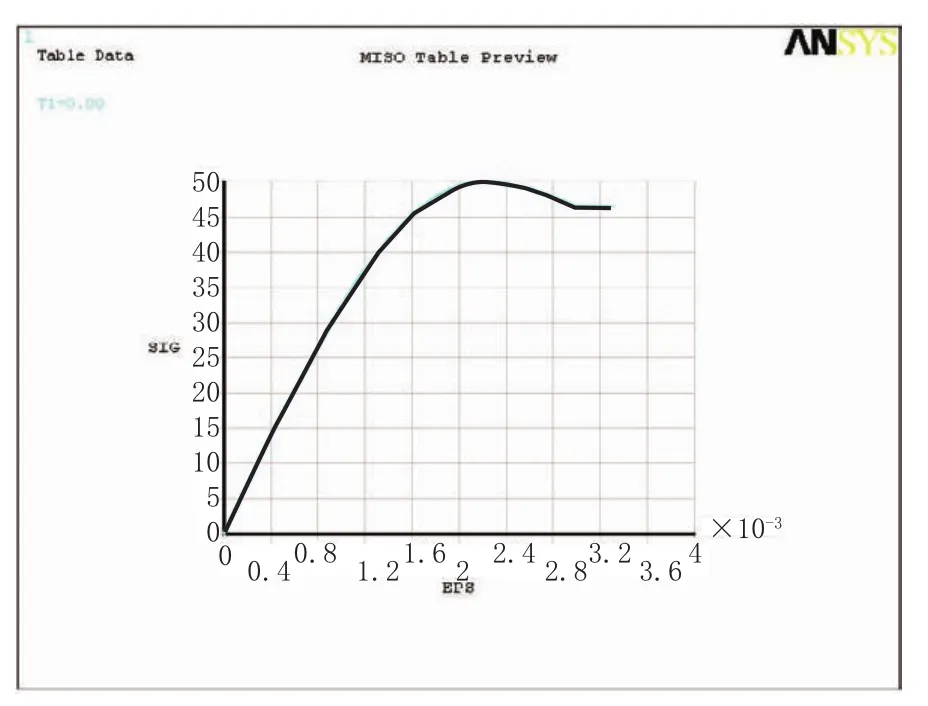
图4 混凝土本构关系图
现阶段具有代表性的混凝土破坏准则有:Willam-Warnke五参数准则、Ottoson四参数准则、Kotsovos五参数准则、Podgorski五参数准则及王传志、过镇海五参数准则等。本文中选用Willam-Warnke五参数准则,其中具体参数分别设为:开裂截面的剪切传递系数βop为0.5;裂缝闭合截面的剪切传递系数βcl为0.95;单轴抗拉强度ft为5;单轴压碎系数设为-1,即不考虑混凝土压碎,以利于计算收敛。
4 加载与求解
为能更好地跟踪预应力混凝土箱梁在荷载各阶段的力学行为,采用多阶段和多子步数进行加载:
(1)张拉阶段:采用等效降温法模拟预应力筋张拉过程。等效降温法不仅可以很好地模拟预应力筋对箱梁的整体作用,也能客观地反映预应力筋各阶段细部的结果。
等效降温法的力学原理为:假设预应力筋只承受温度荷载时发生降温度,则此时预应力筋的形变:
ξ=aΔt,a为材料的线性膨胀系数。
应力:α=Eξ。
本文中预应力筋的张拉应力α=0.75αs= 1 365 MPa,a=0.000 012,E=200 000 MPa,从而得出Δt=-596.15℃。
(2)运营阶段:采用给混凝土箱梁表面加面荷载来模拟承受的汽车、挂车等活荷载,加载直至梁底出现裂缝。
(3)破坏阶段:继续加载,直至混凝土箱梁发生破坏,丧失承受荷载能力。
具体的加载步数如表1所列。
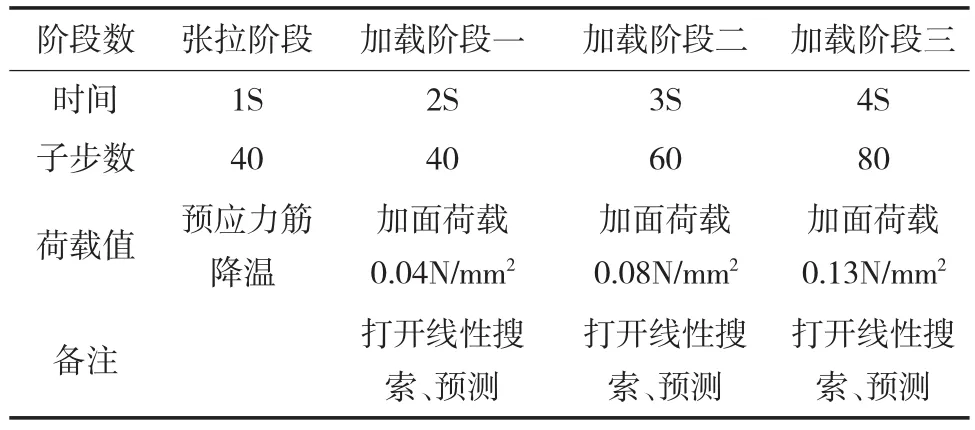
表1 全过程加载情况表
5 结果分析
采用以上有限元模型及加载方案对30m预应力简支箱梁受弯极限承载力全过程模拟分析后,可以得出以下分析结果(具体数值如表2所列):
(1)当对30 m预应力箱梁施加温度荷载后,即达到图5、图6中的A点,此时跨中预应力筋的应力为1 390 MPa,张拉端的预应力筋应力为1 306 MPa;箱梁跨中点的位移达到14.795 mm。预应力张拉的控制应力为1 395 MPa,则损失的预应力为施工过程中的预应力损失值。由于张拉预应力的作用,混凝土箱梁在张拉后形成反拱,见图7所示。最大的反拱发生在跨中节点,为14.795 mm。

表2 特征荷载阶段结果表
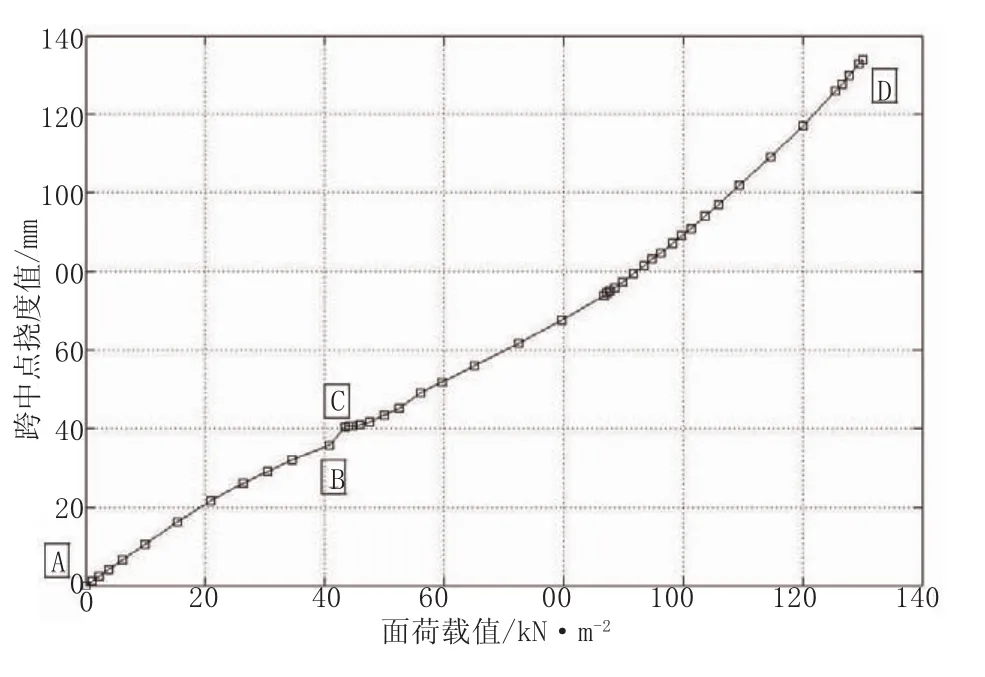
图5 加载全过程跨中点挠度变化图
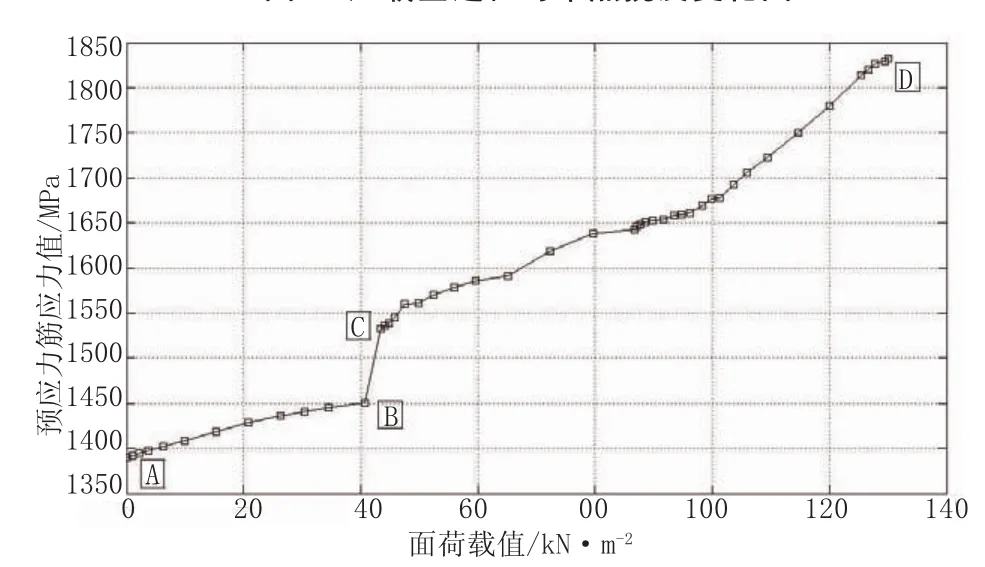
图6 加载全过程跨中预应力筋应力变化图

图7 张拉预应力筋后箱梁形成反拱图示
(2)预应力箱梁张拉完成后,进入箱梁运营阶段,对其箱梁表面加面荷载,当达到图5、图6中的B点时,此时面荷载值为40.735 kN/m2,跨中预应力筋的应力值达到1 450.96 MPa,跨中挠度为35.791 mm。由图5、图6可知从加载阶段A到加载阶段B,荷载值—跨中挠度值及荷载值—跨中预应力筋应力值曲线呈明显的线性关系,说明在此加载阶段过程中,预应力箱梁是处于弹性阶段。
(3)继续对箱梁表面加载,当达到图5、图6中的C点时,此时面荷载值为42.724 kN/m2,跨中预应力筋的应力值达到1 532.66 MPa,跨中挠度为38.851 mm。由图5、图6可知从加载阶段B到加载阶段C,荷载值—跨中预应力筋应力值曲线是一个突变过程,说明在此加载过程中,预应力箱梁底部出现裂缝,拉区混凝土退出工作,拉应力全部由预应力筋承担,预应力筋的应力值由1 450.96 MPa增大到1 532.66 MPa。
(4)当加载阶段由C变化到D点时,此时面荷载值为130 kN/m2,跨中预应力筋的应力值达到1 831.88 MPa,跨中挠度为134.070 mm。由图5、图6可见荷载值—跨中挠度值曲线呈现非线性关系。预应力筋最大应力值为1 834 MPa,达到钢绞线的标准抗拉强度1 860 MPa的98.5%而达到破坏。破坏阶段的预应力筋的应力图及裂纹分布图分别见图8、图9所示。
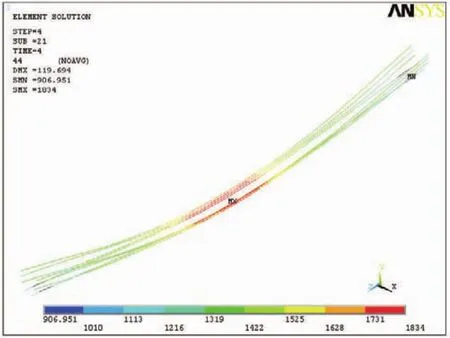
图8 破坏阶段预应力筋应力分布图

图9 破坏阶段预应力箱梁裂纹分布图示
(5)由以上的分析结果可知,在该项仿真分析中预应力箱梁的极限面荷载为130 kN/m2,将箱梁等效为平面梁单元来考虑,取箱梁上表面宽度为2.4 m,则其能承受的极限线荷载为:
U441+4
B
1009-7716(2015)02-0041-03
2014-11-12
庞凌志(1982-),男,山东人,工程师,从事桥梁工程设计工作。
