有限单元法在桩基设计中的应用体会

2015-11-04王根华

建材与装饰 2015年36期

关键词：试桩模拟计算单桩

王根华

（安徽省城乡规划设计研究院）

有限单元法在桩基设计中的应用体会

王根华

（安徽省城乡规划设计研究院）

长期以来，桩基础的设计工作一直是建筑行业的重、难点问题，而确定单桩极限承载力更是桩基设计的关键所在。有限单元法作为确定单桩极限承载力的一种计算方法，因其计算功能强大、方便可靠的特点，在当前已被广泛应用于桩基的设计环节当中，并取得了良好的效果。本文结合钻孔灌注桩现场荷载试验，进行了单桩极限荷载的有限单元的分析，并通过与静载试验结果的对比，证明了有限单元法用于计算和分析单桩极限承载力时具有一定的可靠度与数据精度。

有限单元法；桩基础；设计；应用

在建筑基础选择时，桩基础因其稳定性好、承载力高，沉降稳定、沉降量小而均匀等优点，在建筑工程建设中的得到了广泛的应用与普及，然而由于桩基础属于复杂的力学结构，其工程设计方法至今仍处于半理论、半经验的状态。目前，用于确定桩基承载力的方法主要有弹性理论法、静载试验法和数值分析方法这三种，而弹性理论方法和静载试验法在应用时往往受限条件较多，或者费用昂贵、费时费工。有限单元法作为数值分析方法的主要代表之一，可通过建立逼真的力学与数值模型，包括桩体模型、桩间土几何模型、加载模型以及施工模型等，以较为全面的模拟力的相互作用机理。随着近年来计算机技术的迅速发展，有限单元法在建筑工程中的应用受到了极大的重视，并已显现出了其巨大作用。

1　有限单元法基本理论

随着电子计算机计算的发展和普及，采用数值分析方法研究和计算建筑工程中的各种课题，已成为了近年来建设设计中的一大突破性进展。采用这种方法的最大优点是可以在计算机中，考虑土的实际应力-应变-时间应变关系和复杂的边界条件，把变形、强度和稳定问题综合联系起来进行解决。

使用有限单元法分析计算单桩的沉降与承载力时，可以综合考虑土的非线性应力应变关系与应力水平的影响，还可考虑土体初始应力状态、土的成层性、桩在土中的存在对应力和变形分布的影响，以及成桩工艺对土的应力与变形的影响等等。因此，可以说有限单元法在桩基设计中的应用，是一种综合考虑因素较多，结果较为精确的分析计算方法。

2　工程实例应用研究

2.1工程概况

试验场地为某建筑工程施工现场，场区内地形为南高北低，地面的标高在429.1～432.6m之间。该建筑工程占地面积为150× 90m2，其中建筑总高度为地上十一层，地下一层，基础埋深为7.5m。该试验中的试桩与锚桩均采用的工程桩，试桩数目为三组。

2.1.1场地土质情况

试验场地地基土层主要为：粘土、粉土、壤土及细砂互层。在已勘探深度内，场地地层共有10层土层，层号可用①～⑩进行表述。其中，各层土质的物理力学性质，见表1所示。

2.1.2试桩基本情况

在试验现场选用了3根长度相同的单桩进行垂直荷载试验，标号分别为s1、s2、s3。且每根试桩配置有4根锚桩提供反向作用力，12根锚桩的编号为M1～M12。试桩与锚桩的基本参数值，见表2所示。

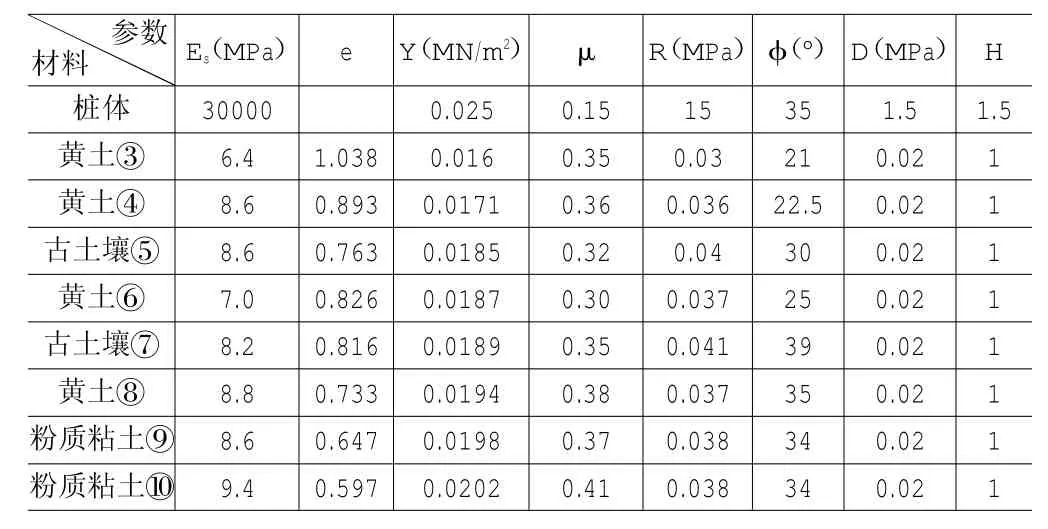
表1　场地各层土质物理力学性质统计表

表2　试桩与锚桩的参数值表

2.2计算方法

2.2.1有限单元模型的建立

由于单桩和周围一定范围的土体是联系在一起的，可作为轴对称体，因此在进行单桩极限承载力分析时，可看作是轴对称问题。在图1中，即为利用计算机程序模拟出的单桩计算模型。从计算模型中可以看出，为有效提高精度，桩端附近的单元划分较细，桩侧水平向与垂直向单元的划分也随之桩轴与桩端距离的接近，而逐渐加密。考虑到桩端侧阻力达到极限以后会出现滑动，以及桩端在应力较大时还会出现拉裂现象，因此在桩端和桩侧分别设置了一维竖向和横向的单元进行模拟。

在图1中，L指桩的入土深度，b为桩的半径，P为垂直荷载。1、2、3、4、5分别是指桩轴线、二维单元、固定边界结点、Z方向接触面单元及r方向接触面单元。

图1　单桩极限承载力有限单元模型

通过单桩计算模型，可以得出荷载-沉降曲线（P-S）、桩身弹性压缩变形曲线（P-H）、桩侧阻力沿深度分布曲线（q-s）、桩端土塑性变形区范围等等。利用有限单元法计算单桩的承载力与沉降，虽然可以考虑到多种因素的影响，但计算结果与计算模型的建立与计算参数的确定有着密切的关系。

2.2.2求解步骤

（1）将估计的单桩极限荷载值分为若干等级，并逐渐添加。由于现场静载试验的加载也是逐级施加的，为方便和静载试验进行比较，在计算过程中也应当与静载试验的荷载情况相一致。

（2）对于每一级荷载的增量P，应先求解出结点荷载值。由于荷载主要作用在桩顶，即所建立的模型网格中有两个结点环，分别在桩轴和桩周。首先加速增量p值均匀分布在桩顶附近，则可按照轴对称原理中的静力等效原则将增量P向结点环位置移动，从而得出桩轴上结点荷载值为1/3P，桩周上结点荷载值为2/3P。

（3）对各单元弹性模量进行求解。若某单元处于破坏状态，则泊松比μ取值0.49，弹性模量Et可认为很小，按照1kg/cm2进行计算；若某单元还没破坏，则泊松比μ值应当为常量，并按照相关方程式计算弹性模量Et。

2.3计算结果分析

2.3.1单桩极限承载能力

在表3中，即为单桩极限承载力的实测值与模拟计算值的对比。经过计算，三个试桩的模拟值误差分别为7.7%、8.9%和7.6%，其误差值在允许的范围以内。证明了有限元法模拟计算时单桩极限承载力时，具有足够的数据精度。

表3　单桩极限承载力的实测值与模拟值对比表

2.3.2荷载-沉降曲线

在图2中，即为现场静载试验值与试桩模拟计算值在荷载-沉降关系曲线的对比图。从图2可以看出，通过有限单元法模拟得到的曲线和静载试验所获得曲线相接近，证明了有限元模型及计算方法的合理性。而且从图2中还可发现模拟计算曲线具有明显的弹性、塑性及破坏这三个阶段的非线性特征。其中，当荷载较小时，曲线近似为直线；随着荷载逐渐增加到极限荷载的过程，曲线逐渐朝下弯曲倾斜，当荷载达到极限荷载时，桩体的沉降急剧加大，模拟曲线也表现为很陡。由此也证明了有限单元法计算模型是满足单桩极限荷载的试验状态的。