香港回归前后中国内地股市与香港股市联动机制的甄别与比较
2015-11-03闫超刘金全王雄威
闫超 刘金全 王雄威


摘要: 本文运用不同方法估计Copula-MGARCH模型,以期在甄别和判断不同估计方法有效性的基础上,选择最优的估计方法透析和测度香港回归前后中国内地股市与香港股市的联动机制。研究结果表明:与IFM估计方法相比较,利用MBP估计方法计算Copula-MGARCH模型更优;与香港回归前相比较,在香港回归至今的17年里,尽管内地股市与香港股市之间的联动显著增强,但是二者之间的联动机制仍然较弱;内地股市在香港回归前呈现显著的波动迹象,但在香港回归后波动态势趋于平缓;与此相反,香港股市在香港回归前的波动幅度较为微弱,回归后波动特征陡然增强,而且这种波动特征持续了近五年之久。
关键词:内地股市;香港股市;Copula-MGARCH模型;MBP估计
中图分类号:F830.59 文献标识码:A
作者简介:闫超(1985-),女,吉林省吉林市人,吉林大学数量经济研究中心讲师,管理学博士,研究方向:宏观经济学、金融计量学、经济计量学;刘金全(1964-),黑龙江密山人,男,吉林大学数量经济研究中心教授,博士生导师,经济学博士,研究方向:宏观经济学、金融计量学、经济计量学;王雄威(1984-),男,江西景德镇人,中国邮政储蓄银行总行职员,经济学博士,研究方向:宏观经济学、金融计量学、经济计量学。
一、引言
近年来,在诸如金融衍生工具定价、投资组合选择、套期保值测算以及金融风险评估等有关金融市场领域的研究当中,金融时间序列数据所呈现出的“波动聚类”现象得到众多学者的空前关注。与此同时,能够刻画和检验金融时间序列“波动性”特征的广义自回归条件异方差(Generalized AutoRegressive Conditional Heteroscedasticity,简称GARCH)模型以及可以描述和测度不同金融市场中“波动性”与“协波动性”之间关系的多变量广义自回归条件异方差(Multivariate Generalized AutoRegressive Conditional Heteroscedasticity,简称MGARCH)模型得到了广泛的应用。
在基于MGARCH模型的大量实证研究当中,学者通常都假设金融时间序列数据服从某个特定的多元椭圆分布类(例如,服从多元正态分布、多元GED分布或者多元Student-t分布等),然而基于多元椭圆分布类的设定,尽管能够简化模型形式,从而更易于模型估计,但是却无法准确描述和刻画金融时间序列数据当中所可能存在的“非线性”、“非对称性”以及“尖峰厚尾分布”等特征。Nelsen(1999)曾强调,在其构建的Copula函数中无需考虑联合分布的具体形式,因此基于Copula函数的相关测度能够较为准确地刻画金融时间序列数据中所具有的非椭圆分布特征。而Patton(2006)通过进一步的研究发现,无论是预测未知样本数据的多变量密度,还是选择已知样本数据的模型标准,与MGARCH模型相比,利用Copula-MGARCH模型可以进一步分析由不同的边际分布和Copula函数共同构成的联合分布函数,从而使得Copula-MGARCH模型的拟合效果明显更优。此外,Palaro和Hotta(2006)通过对美国股票市场在险价值(Value-at-Risk,简称VaR)进行相关研究后,再一次印证,与传统的MGARCH模型相比,由条件Copula-MGARCH模型得到的估计结果更为稳健。在随后的研究中,Chang(2012)以及Li和Yang(2013)基于Copula-MGARCH模型刻画了原油期货市场特征,Wang等(2010)以及Aloui等(2013)基于Copula-MGARCH模型测度了外汇风险情况,Deng(2011)以及Laih(2014)基于Copula-MGARCH模型探讨了股票市场收益率问题。在国内的相关研究中,刘金全和隋建利(2010)以及张自然和丁日佳(2012)探讨了Copula-MGARCH模型在汇率市场中应用的可行性。梁建峰等(2011)以及史美景和赵永淦(2012)分别基于外汇市场以及股指现货、期货市场的研究证明,基于Copula-MGARCH模型估计股指期货套期保值效果更优。此外,吴恒煜和胡根华(2013)基于Copula-MGARCH模型对欧洲气候交易所EUA和CER的现货市场与期货市场之间的动态相依性进行了分析。
与其他MGARCH模型相比较,虽然Copula-MGARCH模型具有较多优势,但我们发现,目前国内却鲜有学者基于Copula-MGARCH模型对我国股票市场进行详尽而深入的探究,更少有学者充分利用Copula-MGARCH模型具有的优势,从香港回归前后的不同时域范围出发,甄别和透析香港回归前后中国内地股市与香港股市联动机制是否存在显著的差异。
此外,就多变量模型的具体估计方法而言,由于精确极大似然(Exact Maximum Likelihood,简称EML)估计方法无法对多变量模型中的所有参数都进行准确估计,因此Shih和Louis(1995)基于两阶段思想而提出的IFM(Inference Function for Margin)估计方法在对多变量模型的估计过程中得到了普遍的应用。总体上,目前在关于多变量模型估计方法选择的相关理论与实证研究文献当中,众多学者大都集中于运用一步修正EML估计方法抑或IFM估计方法。然而Song等(2005)却指出,就具体计算来讲,虽然与EML估计方法相比较,IFM估计方法更加简便,但是当所研究的时间序列数据总体样本容量相对较小时,基于IFM估计方法所获得的最终估计结果会产生相对较大的估计误差,亟需进一步寻求能够有效估计多变量模型参数的有效、可靠方法。
正是鉴于上述多方面的考虑,在本文中,我们首先基于上证综合指数日收盘价和香港恒生指数日收盘价时间序列数据,进一步计算出上证综合指数和香港恒生指数日收益率时间序列数据,随后构建拟合效果相对更优的Copula-MGARCH模型,并分别利用IFM估计方法以及Liu和Luger(2009)提出的MBP(Maximization by Parts)估计方法进行具体估计。我们不仅旨在甄别和判断IFM估计方法以及MBP估计方法的有效性问题,更重要的是,我们要选择最为有效的估计方法来透析和测度香港回归前后,中国内地股票市场与香港股票市场的特征及其联动机制问题。此外,作为比较与参考,在本文中,我们还选取伦敦金融时报100指数日收盘价时间序列数据计算出其日收益率时间序列数据,以期描绘英国股票市场走势。
二、MBP估计方法的描述与Copula-MGARCH模型的构建
作为讨论的起点,在此我们首先简要介绍MBP估计方法,进而简要阐述基于MBP估计方法对Copula-MGARCH模型各参数的具体估计过程。
(一)MBP估计方法的描述
首先我们将完整对数似然函数具体分解为两个不同层面:第一层面是构建一个简单的对数似然函数,第二层面则是基于第一层面所获得的具体结果所进行的后续估计。在此,我们考虑如下形式的对数似然函数:
如果将上述步骤进行重复迭代,那么θ1和θ2的估计量就能够最终收敛于EML估计量。需要特别指出的是,由于IFM估计方法仅涵括了MBP估计方法的Step 1.1以及Step 1.2两个步骤,因此可以将IFM估计方法视为MBP估计方法的一个特殊情况。在本文当中,我们将着重基于MBP估计方法对涵括正态边际分布的双变量Gaussian Copula-MGARCH模型进行系统而全面的估计。
三、香港回归前后中国内地股市与香港股市联动机制的实证检验
基于本文所构建的具体模型以及所介绍的参数估计方法,我们选取上证综合指数日收盘价时间序列数据(PSH)和香港恒生指数日收盘价时间序列数据(PHS),并利用t期和t-1期的指数日收盘价序列Pt和Pt-1进一步计算与其相对应的t期指数日收盘价对数收益率序列Rt,即Rt=100[ln(Pt)-ln(Pt-1)],从而以上证综合指数日收益率时间序列数据(RSH)表征中国内地股票市场运行态势,以香港恒生指数日收益率时间序列数据(RHS)刻画香港股票市场运行特征,旨在详细测度和透析上证综合指数日收益率序列RSH与香港恒生指数日收益率序列RHS之间的联动机制问题①。作为比较与参考,在本文中,我们还选取伦敦金融时报100指数日收盘价时间序列数据(PFTSE),并进而计算出伦敦金融时报100指数日收益率时间序列数据(RFTSE),以期描绘英国股票市场走势。本文所研究的样本区间为1991年1月2日至2014年9月30日。考虑到自1997年7月1日起,经历百年沧桑的香港回归祖国,中国政府对香港恢复行使主权,本文以1997年7月1日为期界,将总样本区间具体划分为两个不同的时域范围,从而具体甄别和比较香港回归前后中国内地股市与香港股市之间的联动机制问题。数据源自于锐思(RESSET)金融研究数据库,文中所涉及的所有程序由EViews 8.0、R、Gauss 9.0及Ox 6.0语言所编写计算完成。
图1至图6分别鲜明地刻画出上证综合指数日收盘价时间序列、上证综合指数日收益率时间序列、香港恒生指数日收盘价时间序列、香港恒生指数日收益率时间序列、伦敦金融时报100指数日收盘价时间序列、伦敦金融时报100指数日收益率时间序列的时间动态轨迹。其中,图1、图3和图5中的“趋势成分”是基于Hodrick和Prescott(1997)提出的H-P(Hodrick-Prescott)滤波技术计算得到的,旨在刻画上证综合指数日收盘价、香港恒生指数日收盘价和伦敦金融时报100指数日收盘价的总体运行态势,而“波动成分”则具体刻画了上证综合指数日收盘价、香港恒生指数日收盘价和伦敦金融时报100指数日收盘价与其“趋势成分”之间的差距,用以表征其波动程度。
由图1、图3和图5我们可以发现,伴随着时间的推移,上证综合指数日收盘价时间序列和香港恒生指数日收盘价时间序列的时间波动路径并不十分相近,例如,从近期的发展趋势而言,上证综合指数日收盘价呈现出总体下行的态势,而香港恒生指数日收盘价却呈现出总体攀升的势头,这一点可以从上证综合指数日收盘价和香港恒生指数日收盘价二者的“趋势成分”时间动态轨迹中得到清晰的印证。此外,通过观察上证综合指数日收盘价和香港恒生指数日收盘价的“波动成分”,我们发现,上证综合指数日收盘价在1993年前后以及2007年下半年至2010年期间(即源于美国次贷危机而引发全球金融危机的期间内)表现出较为显著的大幅波动迹象,香港恒生指数日收盘价在香港回归后的几年内以及全球金融危机爆发期间呈现出剧烈的宽幅波动态势。最后,纵观香港回归前以及香港回归后的总体时间范围,我们发现,伦敦金融时报100指数日收盘价时间序列和香港恒生指数日收盘价时间序列的时间波动路径较为相近,仅在香港刚回归后的几年时间范围内,二者的时间波动路径有所不同。
就图2、图4和图6所示的日收益率而言,无论是上证综合指数日收益率时间序列,还是香港恒生指数日收益率时间序列,抑或是伦敦金融时报100指数日收益率时间序列,均体现出了显著的“波动聚类”特征,而这种“波动聚类”特征则表明收益率的变化常常伴随着相应的价格改变,也就是说,在一定的期限范围内,宽幅的收益率变化通常都伴随着剧烈的价格波动,而小幅的收益率改变所对应的价格波动则通常较为微弱。此外,我们还注意到,在香港回归之前的时间范围内,香港恒生指数日收益率时间序列的波动态势相对较为微弱,而上证综合指数日收益率时间序列的波动态势相对更为剧烈。自香港回归之日起,上证综合指数日收益率时间序列的波动态势陡然削弱,而香港恒生指数日收益率时间序列却骤然呈现出显著并持续多年的波动迹象。在最近十年左右的期限范围内,上证综合指数日收益率时间序列和香港恒生指数日收益率时间序列总体呈现出大体相似的波动路径,例如,在2007年下半年至2010年期间,即在全球金融危机爆发时期,上证综合指数日收益率时间序列和香港恒生指数日收益率时间序列都凸显出剧烈的波动形态。最后,我们还发现,无论是香港回归以前还是香港回归之后,总体而言,伦敦金融时报100指数日收益率时间序列和香港恒生指数日收益率时间序列在剧烈与微弱的波动时机方面、宽幅与小幅的波动程度层面都较为同步。
我们在表1中详细给出了上证综合指数日收益率序列RSH、香港恒生指数日收益率序列RHS和伦敦金融时报100指数日收益率序列RFTSE的描述性统计量计算结果。我们发现,偏度统计量以及峰度统计量的计算结果都一致表明,上证综合指数日收益率、香港恒生指数日收益率和伦敦金融时报100指数日收益率序列均呈现出极为明显的“尖峰厚尾”分布特征;此外,由Ljung-Box Q统计量计算结果可以进一步判断,上证综合指数日收益率、香港恒生指数日收益率和伦敦金融时报100指数日收益率序列均存在显著的条件异方差性特征。因此,本文基于GARCH(1, 1)模型对其进行系统研究科学而可靠。
我们发现,在香港回归前,上证综合指数日收益率RSH和香港恒生指数日收益率RHS序列二者之间的相关系数为ρ=0.028;在香港回归后,上证综合指数日收益率RSH和香港恒生指数日收益率RHS序列二者之间的相关系数为ρ=0.169。在香港回归前,伦敦金融时报100指数日收益率RFTSE和香港恒生指数日收益率RHS序列二者之间的相关系数为ρ=0.249;在香港回归后,伦敦金融时报100指数日收益率RFTSE和香港恒生指数日收益率RHS序列二者之间的相关系数为ρ=0.378。在香港回归前,上证综合指数日收益率RSH和伦敦金融时报100指数日收益率RFTSE序列二者之间的相关系数为ρ=0.011;在香港回归后,上证综合指数日收益率RSH和伦敦金融时报100指数日收益率RFTSE序列二者之间的相关系数为ρ=0.014。这意味着,一方面,无论是香港回归前还是香港回归后,中国内地股票市场与英国股票市场之间的联动机制最弱,香港股票市场与英国股票市场之间的联动机制最强,而中国内地股票市场与香港股票市场之间的联动机制居中。对于这一论断,我们已然有所预判,并且完全可以从现实情况中直接获得解释。另一方面,与香港回归前的时期相比较,中国内地股票市场与英国股票市场之间的联动机制在香港回归后依旧极其微弱,香港股票市场与英国股票市场之间的联动机制在香港回归后呈现出微弱的提高,而中国内地股票市场与香港股票市场之间的联动机制在香港回归后显著增强。然而,尽管联动机制显著增强了,但是亟待我们深入探究和透析的问题却是在香港回归后的17年里,究竟是什么原因导致中国内地股市与香港股市之间的联动机制仍然较为微弱?
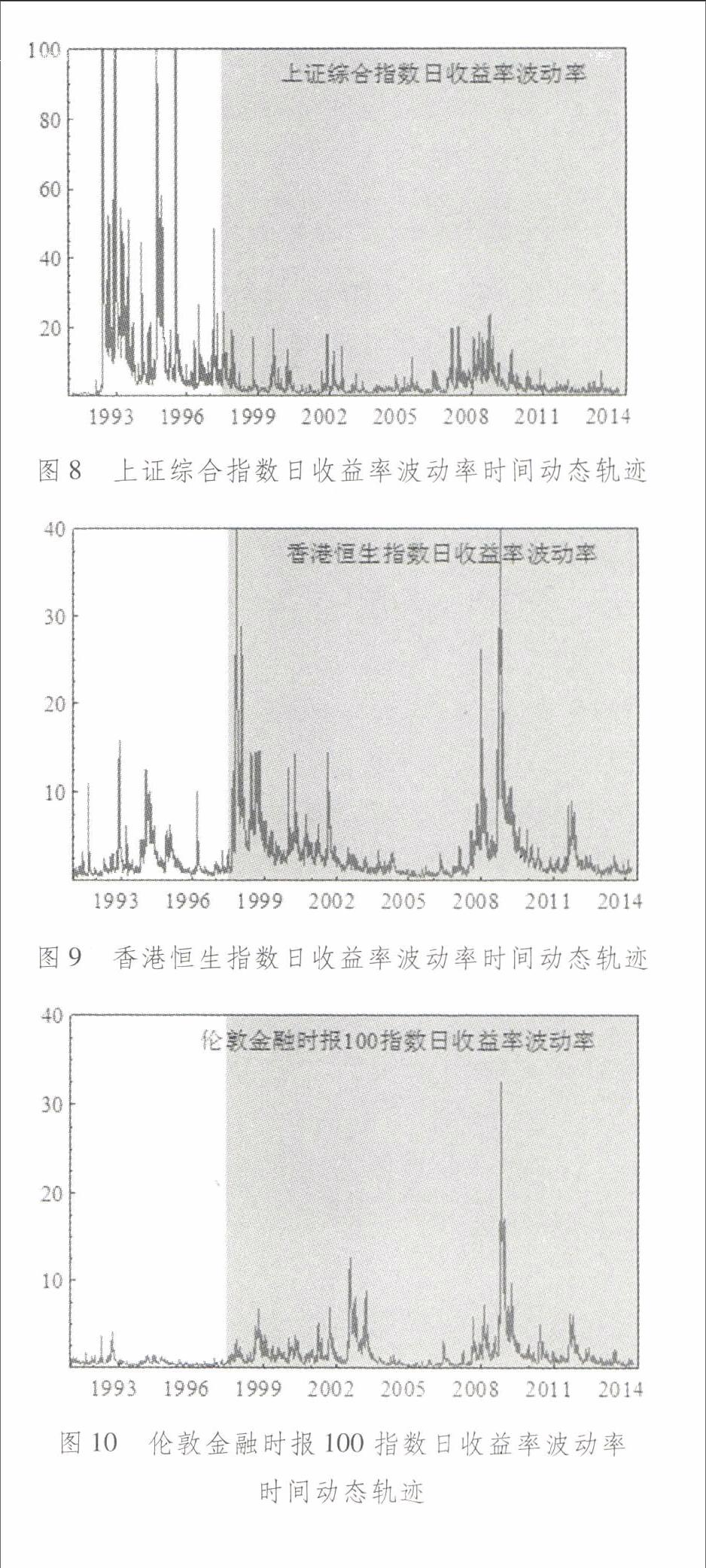
为了深入剖析香港回归前后,中国内地股市与香港股市之间联动机制较为微弱的深层次缘由,我们运用相对更优的MBP估计方法,基于Copula-MGARCH模型对上证综合指数日收益率时间序列和香港恒生指数日收益率时间序列数据进行进一步估计,从而获得如图8和图9所示的上证综合指数日收益率波动率和香港恒生指数收益率波动率的时间动态轨迹。我们可以清晰地发现,与图2和图4所示的直观刻画相吻合,上证综合指数日收益率波动率时间序列在香港回归之前表现出显著的剧烈波动迹象,而自香港回归以来,上证综合指数日收益率波动率时间序列的波动迹象骤然趋于平缓,仅在2007年下半年至2010年期间,即源于美国次贷危机而引发全球金融危机的期间内,其波动迹象有所凸显。香港恒生指数日收益率波动率时间序列在香港回归之前的时间范围内相对较为平缓,但是自香港回归之日起,香港恒生指数日收益率波动率时间序列的波动特征陡然增强,而且,这种相对剧烈的波动特征持续了近五年之久。此外,自2007年下半年起,受国际金融危机的冲击和波及影响,香港恒生指数日收益率波动率序列再一次呈现显著上扬的态势。最后,从步入后金融危机起至今,就发展趋势而言,香港恒生指数日收益率波动率呈现出跌宕起伏的形态,而上证综合指数日收益率波动率却处于相对较为平缓的低位波动。同样,我们在此也基于Copula-MGARCH模型对伦敦金融时报100指数日收益率时间序列数据进行估计,从而获得如图10所示的伦敦金融时报100指数日收益率波动率的时间动态轨迹。可以看出,伦敦金融时报100指数日收益率波动率虽然比香港恒生指数日收益率波动率更为微弱,但大体而言,却与香港恒生指数日收益率波动率的时间波动路径较为相似,尤其是在香港回归之后的期间范围内,二者几乎在相同的时间范围内呈现出较为剧烈的波动态势。这意味着,虽然香港回归至今已有17年,但要真正实现与香港股市之间更为密切的联动发展,中国内地股市在改革、健全与完善等诸多方面依旧任重而道远。
四、主要结论与经济政策启示
本文在构建Copula-MGARCH模型的基础上,通过甄别和判断MBP估计方法和IFM估计方法的有效性,选择最为有效的MBP估计方法透析和测度了香港回归前后,中国内地股票市场和香港股票市场之间的联动机制问题,获得如下重要的认识和判断:
首先,由于MBP估计方法的收敛速度取决于所具体测度的时间序列的样本数量(Liu和Luger,2009;刘金全和隋建利,2010),为了保证实证研究的可靠性和稳健性,我们基于上证综合指数日收益率时间序列和香港恒生指数日收益率时间序列中的前500个样本数据,在估计Copula-MGARCH模型时,通过刻画由MBP估计方法所获得的参数估计值与由EML估计方法所获得的参数估计值之间的平均距离,发现MBP估计方法比IFM估计方法更有效。此外,条件方差与条件协方差矩阵均值估计结果和方差估计结果都表明,与IFM估计方法相比较,运用MBP估计方法所得到的条件方差与条件协方差矩阵的方差值更小,换句话说,IFM估计方法较MBP估计方法过度估计了条件方差与条件协方差矩阵。进一步基于均方根误差(RMSE)判别准则和绝对离差(MAD)判别准则,并通过考虑百分比,即RMSE(%)和MAD(%)指标的检验结果均表明,由IFM估计方法所获得的结果均大于由MBP估计方法所获得的结果,这再一次印证,在具体计算Copula-MGARCH模型时,与IFM估计方法相比较,MBP估计方法更优。
其次,利用MBP估计方法的检验结果表明,一方面,无论是香港回归前还是香港回归后,中国内地股票市场与英国股票市场之间的联动机制最弱,香港股票市场与英国股票市场之间的联动机制最强,而中国内地股票市场与香港股票市场之间的联动机制居中;另一方面,与香港回归前的时期相比较,尽管中国内地股票市场与香港股票市场之间的联动机制在香港回归后显著增强,但是,与香港和英国股市之间的联动性相比,中国内地股市与香港股市之间的联动机制仍然较为微弱,如何提高二者之间的联动机制是我们亟需思考的一个重要问题。
最后,基于MBP估计方法的检验结果表明,一方面,上证综合指数日收益率波动率时间序列在香港回归之前表现出显著的剧烈波动迹象,但自香港回归以来,上证综合指数日收益率波动率时间序列的波动迹象骤然趋于平缓,仅在源于美国次贷危机而引发全球金融危机的期间内,其波动迹象有所凸显。另一方面,香港恒生指数日收益率波动率时间序列在香港回归之前的时间范围内相对较为平缓,但是自香港回归之日起,香港恒生指数日收益率波动率时间序列的波动特征陡然增强,而且,此相对剧烈的波动特征持续了近五年之久。此外,自2007年下半年起,受国际金融危机的冲击和波及,香港恒生指数日收益率波动率序列再一次呈现显著上扬的态势。
注释:
① 我们在锐思(RESSET)金融研究数据库中所获得的深证综合指数日收盘价数据的起始时间为1991年4月3日,所获得的上证综合指数日收盘价数据的起始时间为1990年12月19日,所获得的香港恒生指数日收盘价数据的起始时间为1986年12月31日。考虑到所研究数据的“时间一致性”问题,同时由于论文篇幅有限,在本文中,我们只选取上证综合指数日收盘价序列表征中国内地股票市场运行态势。
参考文献:
[1] 梁建峰,陈健平,刘京军.基于Copula-GARCH方法的LPM套期保值研究[J].系统工程学报, 2011(5): 636-641.
[2] 刘金全, 隋建利.Copula-MGARCH模型及其估计方法在汇率市场中的应用[J].数量经济技术经济研究, 2010(7): 91-104.
[3] 史美景, 赵永淦.基于Copula-TGARCH模型的股指期货最佳套期保值比研究[J].数理统计与管理, 2012(3): 352-362.
[4] 吴恒煜, 胡根华.国际碳排放权市场动态相依性分析及风险测度: 基于Copula-GARCH模型[J].数理统计与管理, 2013(12): 158-169.
[5] 张自然, 丁日佳.人民币外汇市场间不对称汇率变动的实证研究[J].国际金融研究, 2012(2): 85-95.
[6] Aloui, r., Assa, M. S., Nguyen, D. K. Conditional Dependence Structure between Oil Prices and Exchange Rates: A Copula-GARCH Approach[J].Journal of International Money and Finance, 2013, 32(4): 719-738.
[7] Chang, K. L. The Time-Varying and Asymmetric Dependence between Crude Oil Spot and Futures Markets: Evidence from the Mixture Copula-Based ARJI-GARCH Model[J].Economic Modelling, 2012, 29(6): 2298-2309.
[8] Deng, l., Ma, C. Q., Yang, W. Y. Portfolio Optimization via Pair Copula-GARCH-EVT-CVaR Model[J].Systems Engineering Procedia, 2011, 36(2): 171-181.
[9] Hodrick, R. J., Prescott, E. C. Postwar U.S. Business Cycles: An Empirical Investigation[J].Journal of Money, Credit and Banking, 1997, 29(1): 1-16.
[10]Jondeau, E., Rockinger, M. The Copula-GARCH Model of Conditional Dependencies: An International Stock Market Application[J].Journal of International Money and Finance, 2006, 25(4): 827-853.
[11]Laih, Y. W. Measuring Rank Correlation Coefficients between Financial Time Series: A GARCH-Copula based Sequence Alignment Algorithm[J].European Journal of Operational Research, 2014, 232(2): 375-382.
[12]Li, M., Yang, L. Modeling the Volatility of Futures Return in Rubber and Oil-A Copula-Based GARCH Model Approach[J].Economic Modelling, 2013, 35(2): 576-581.
[13]Liu, Y., Luger, R. Efficient Estimation of Copula-GARCH Models[J].Computational Statistics and Data Analysis, 2009,53(6):2284-2297.
[14]Nelsen, R. B. An Introduction to Copulas[M].New York: Springer-Verlag, 1999: 66-96.
[15]Palaro, H. P., Hotta, L. K. Using Conditional Copula to Estimate Value at Risk[J].Journal of Data Science, 2006,86(4): 93-115.
[16]Patton, A. J. Estimation of Multivariate Models for Time Series of Possibly Different Lengths[J].Journal of Applied Econometrics, 2006,21(12): 147-173.
[17]Shih, J. H., Louis, T. A. Inferences on the Association Parameter in Copula Models for Bivariate Survival Data[J].Biometrics, 1995,51(6): 1384-1399.
[18]Song, P., Fan, Y., Kalbfleisch, J. Maximization by Parts in Likelihood Inference[J].Journal of the American Statistical Association, 2005,100(4): 1145-1158.
[19]Wang, Z. R., Chen, X. H., Jin, Y. B., Zhou Y. J. Estimating Risk of Foreign Exchange Portfolio: Using VaR and CVaR based on GARCH-EVT-Copula Model[J].Physica A: Statistical Mechanics and its Applications, 2010, 389(21): 4918-4928.
(责任编辑:张曦)
