A research on film thickness of a typical dynamic seal for hydraulic actuators
2015-11-03ZhigangLIANJuanjuanSUNYanliangDONG
Zhi-gang LIAN, Juan-juan SUN, Yan-liang DONG
(1School of Mechanical and Electrical Engineering, Harbin Institute of Technology, Harbin 150080, China) (2Shenzhen Mindray Bio-medical Electronics Co.,LTD, Shenzhen 518057, China)
A research on film thickness of a typical dynamic seal for hydraulic actuators
Zhi-gang LIAN1*, Juan-juan SUN2, Yan-liang DONG1
(1School of Mechanical and Electrical Engineering, Harbin Institute of Technology, Harbin 150080, China) (2Shenzhen Mindray Bio-medical Electronics Co.,LTD, Shenzhen 518057, China)
This paper studies the film thickness of dynamic seals at the contact of vanes and cylinder which are used in swing motor. A mathematical model is established for the combined seal structure, and the film thickness in sealing gap is gotten by calculating the amount of each part’s deformation. The established mathematical model takes these factors, such as sealing pressure, relative sliding velocity as well as the physical characteristics of the seal on the film thickness, into account, which provides evidences for improving the dynamic sealing performance.
Polytetrafluoroethylene, Contact surface displacement, Thermoelasticity, Film thickness
1 Introduction
Hydraulic system has been widely used in modern engineering, and the reliability of the seals of hydraulic system is of great significance to the hydraulic system. The combined seals, composed of a sealing ring and an O-ring, is a typical sealing form used in modern hydraulic system. However, the way to evaluate the performance of this kind of seals still depends on experience, and which has not yet been studied and verified theoretically.
The study on hydraulic seals began in the 20th century and had a rapid development in the 1960s. White and Denny researched on reciprocating seals and carried out experiments, which made the sealing research a breakthrough, between 1944 and 1947 [1-2]. In the 1960s, Swales and Dowson combined the theoretical predictions with experiment through the elastic hydrodynamic lubrication theory, which made research on hydraulic seals further leaps [3].
In the present study, a mathematical model is established through the elastic hydrodynamic lubrication and the mechanics of the seals, which considers the impact of the sealing environment and the physical characteristics on dynamic sealing performance, and then explores the influence of physical quantities on the film thickness in sealing gap.
2 Mathematical models of dynamic seal
2.1 Seal structure
The present study based on dynamic sealing structure of a swing motor at the contact of vanes and cylinder is shown in Fig.1. The seal is composed of a sealing ring and an O-ring, in which the material of sealing ring is polytetrafluoroethylene, and O-ring is made of nitrile rubber.
2.2 Elastic hydrodynamic lubrication
The film thickness in sealing gap is mainly concerned with sealing pressure, relative sliding velocity and some other factors. Therefore, the calculation of film thickness can take use of Reynolds equation. Assuming that the state of the film is steady and the dynamic sealing structure of this study is a one-dimensional model, thus one-dimensional Reynolds equation is applicable. The basic form of one-dimensional Reynolds equation is taken as the equation (1).
(1)
where, h is the film thickness in sealing gap, V is the relative sliding velocity, ρ is the fluid destiny, and η is the fluid dynamic viscosity.
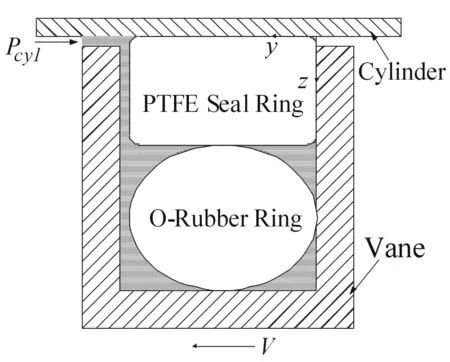
Fig. 1 Seal structure of swing motor
2.3 Kinematical boundary conditions

(2)
where, μ is the boundary friction coefficient of the contact surface of the seal.
2.4 Elastic displacement due to seal pressure and temperature gradient
After adding sealing pressure into the seal tank of swing motor, the seal will be deformed due to the sealing pressure pcy1, and the swing motor will generate heat during the process of operation according to friction and other factors, which will cause the displacement of cylinder and vanes. If ubodyand uvaneare the radial displacement of inner surface of the body and the radial displacement of outer surface of the vane, then
where, Dbodyis the inner diameter of the cylinder; dvaneis the outer diameter of the vane; E, υ, α are the elastic modulus, Poisson’s ratio and the expansion coefficient, respectively; θ is the operating temperature; θ0is the temperature during the installation.
2.5 Surface displacement of the cylinder
At the body-seal contact, the film thickness is governed by pressure and traction from the fluid-solid and solid-solid interaction. A similar method can be used to obtain the displacement of the contact surface of the cylinder, as in Chapter 3 of Johnson [4],
(5)
(6)
then, at the solid-seal contact, the displacement of inner surface of the cylinder is
(7)
2.6 Surface displacement of the seal

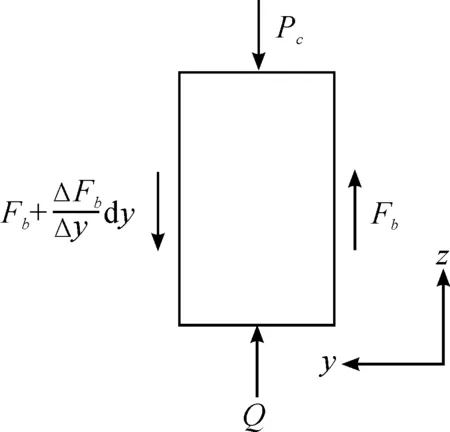
Fig. 2 Stress Analysis of the Seal
The forces from the compression in the sealing house are Pc(at the cylinder-seal contact) and Q (at the housing-seal contact). Forces Fbin Fig. 2 are shear forces. Then
(8)
where, Gsealis the shear modulus of the seal, and uzis the surface displacement of the rectangular strip. Finally, according to the force balance of Oz axis, the equation is worked out to be
(9)
2.7 Thermo-elastic stress of the seal
Due to linear elastic theory, the relationship between stress and strain turns out:
(10)
where, Esealis the elastic modulus of the seal, υsealis the Poisson ratio of the seal, and αsealis the expansion coefficient of the seal.
1) Zero sealing pressure (pcy1=0)
Ifpcy1=0, andσy=-pcy1, thenσy=0. Assuming that ΔR is the initial radial interference of the seal at the temperature of installation, and Dsealis the outer diameter at the temperature of installation, the normal strainεzofthesealiscalculatedastheformula
(11)
Ifp0isthepressureatthecylinder-sealcontact,thenσz=-p0.Takeitintoformula(10),then
(12)
2)Nonzerosealingpressure(pcy1≠0)
Assumingthatpcy1≠0,andσy=-pcy1,thenσy≠0.Ifpconisthepressureatthehousing-sealcontact,pconcanbecalculatedfromthefollowingformulaasinCase(1),
(13)
where,pconisanaveragevalue.
2.8 Film thickness
Thesections2.1to2.7haveanalyzedthekinematicboundaryconditionsandthemechanicaldeformationoftheseal,thecylinderandthevane.Thus,thefilmthicknessinsealinggapcanbecalculatedasfollow,
(14)
3 Applications and results
Themathematicalmodelestablishedtakesmanyfactorsintoaccount,andconsistsofpartialdifferentialequations,thereforethemodelappearstobemorecomplicatedtosolve.Inthispaper,anumericalequationusedthecenterdifferentialisintroducedtogetthediscretevalues.TheflowchatofthemodelisshowninFig. 3.

Fig. 3Theflowchartofthemodel
Thispaperdealswiththefundamentalresultsofthemodelsuchasthecontactpressureandfilmthicknessmaps.TheparametersareshowninTable1.
Table1Solutionparameters
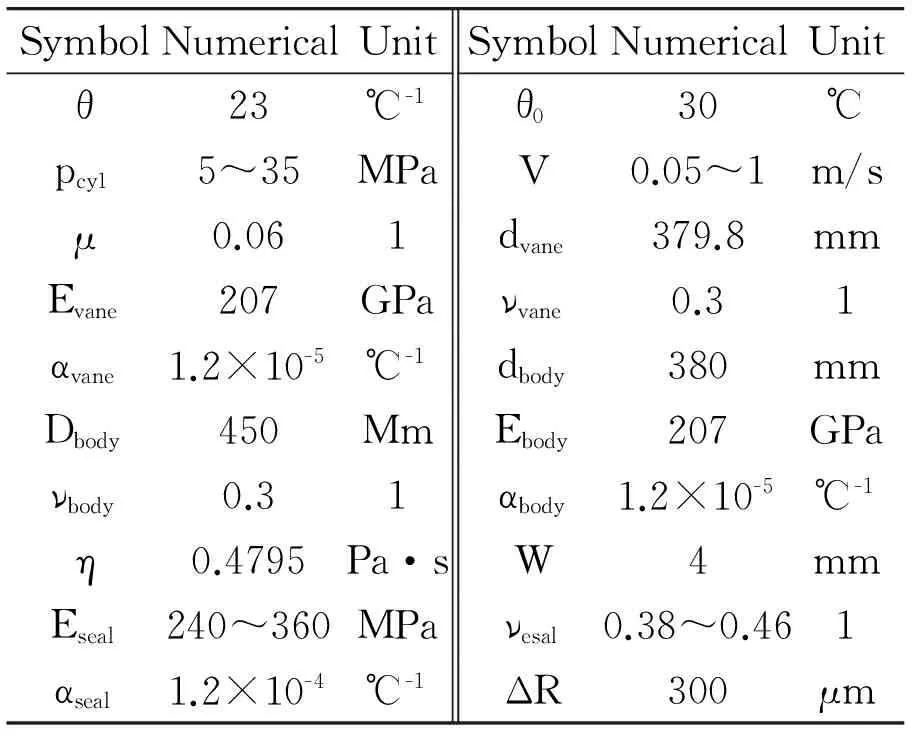
SymbolNumericalUnitSymbolNumericalUnitθ23℃-1θ030℃pcy15~35MPaV0.05~1m/sμ0.061dvane379.8mmEvane207GPaνvane0.31αvane1.2×10-5℃-1dbody380mmDbody450MmEbody207GPaνbody0.31αbody1.2×10-5℃-1η0.4795Pa·sW4mmEseal240~360MPaνesal0.38~0.461αseal1.2×10-4℃-1ΔR300μm
In the hydraulic dynamic sealing, the sealing environment and physical properties of the seal have great impacts on the film thickness. Therefore, the effect of these factors on the film thickness will be discussed in the following chapter.
3.1 The influence of sealing pressure on film thickness
Setting and remaining the initial compression of the seal, assuming that the relative sliding velocity is 100 mm/s, the elastic modulus of the seal is 280 MPa and the Poisson ratio of the seal is 0.4, calculating the film thickness at the sealing pressure 5 MPa, 15 MPa, 25 MPa and 35 MPa, the distribution of the pressure and film thickness in sealing gap is shown in Fig. 4 and Fig. 5.

Fig. 4 The distribution of pressure under different sealing pressure

Fig. 5 The film thickness under different sealing pressure
In Fig. 4, it can be seen that the distribution of pressure at the contact is relatively stable and changes not too much. The pressure at the contact is mainly related to the initial compression and the sealing pressure. Fig. 5 shows that the distribution of film thickness is almost wedge-shaped and the film thickness at the exit of the gap increases as the sealing pressure get increased, but the range is 0-2 μm, which fits to the theoretical value. In summary, the film thickness will increase when the seal pressure is greater, which makes the leakage larger and has a bad impact on the sealing performance.
3.2 The influence of relative sliding velocity on film
thickness
Setting and remaining the initial compression of the seal, assuming that the sealing pressure is 25 MPa, the elastic modulus of the seal is 280 MPa and the Poisson ratio of the seal is 0.4, calculating the film thickness at the relative sliding velocity 0.05 m/s, 0.1 m/s, 0.5 m/s and 1 m/s, the distribution of the pressure and film thickness in sealing gap are shown in Fig. 6 and Fig. 7.
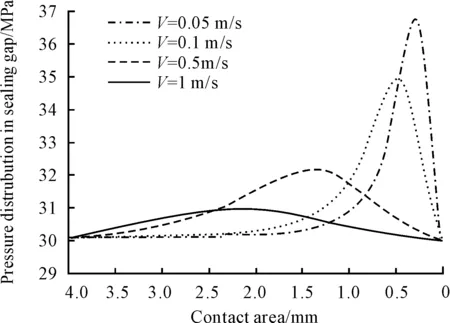
Fig. 6 The distribution of pressure under different relative sliding velocity
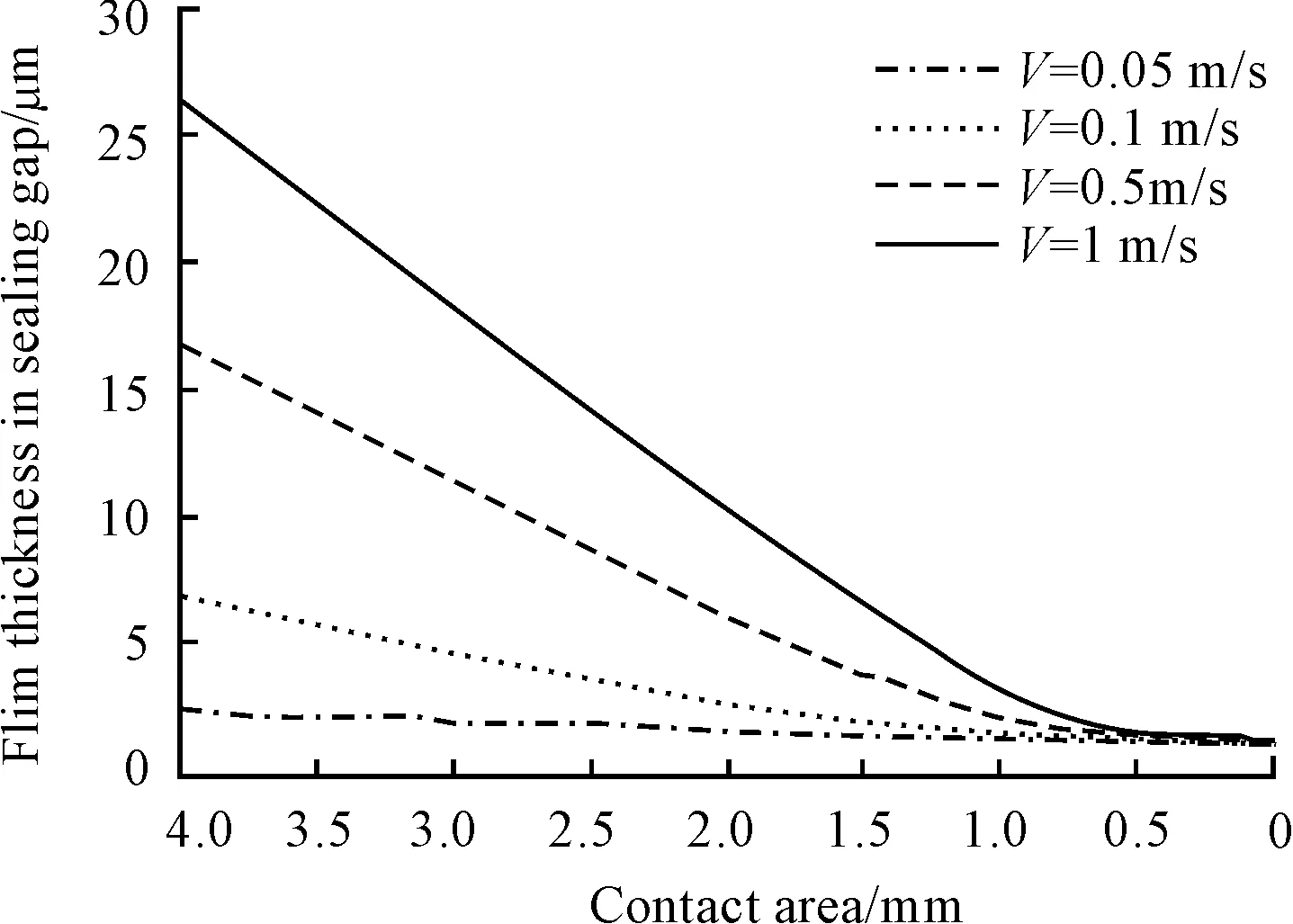
Fig. 7 The film thickness under different relative sliding velocity
In Fig. 6, it can be seen that the pressure peak along the cylinder-seal contact has a trend to move to the entry of film and its value will decrease when the relative sliding velocity grows. While the pressure at the entry and exist is nearly equal. In Fig. 7, the film at the exist changes little, but the average film thickness increases with the rise of relative sliding velocity. In summary, the increasing relative sliding velocity results in the rise of average film thickness. At the same time, the volume of fluid through the cross-section of the sealing gap will expand, which leads to more leakage and has bad impact on the dynamic sealing performance. Therefore, the relative sliding velocity is one of the most important factors that affect the film thickness and the dynamic sealing performance.
3.3 The influence of elastic modulus on film thickness
Setting and remaining the initial compression of the seal, assuming that the sealing pressure is 25 MPa, the relative sliding velocity is 0.1 m/s, and the Poisson ration of the seal is 0.4, calculating the film thickness at the elastic modulus of the seal 240 MPa, 280 MPa, 320 MPa and 360 MPa, the distribution of the pressure and film thickness in sealing gap are shown in Fig. 8 and Fig. 9.

Fig. 8 The distribution of pressure under different elastic modulus
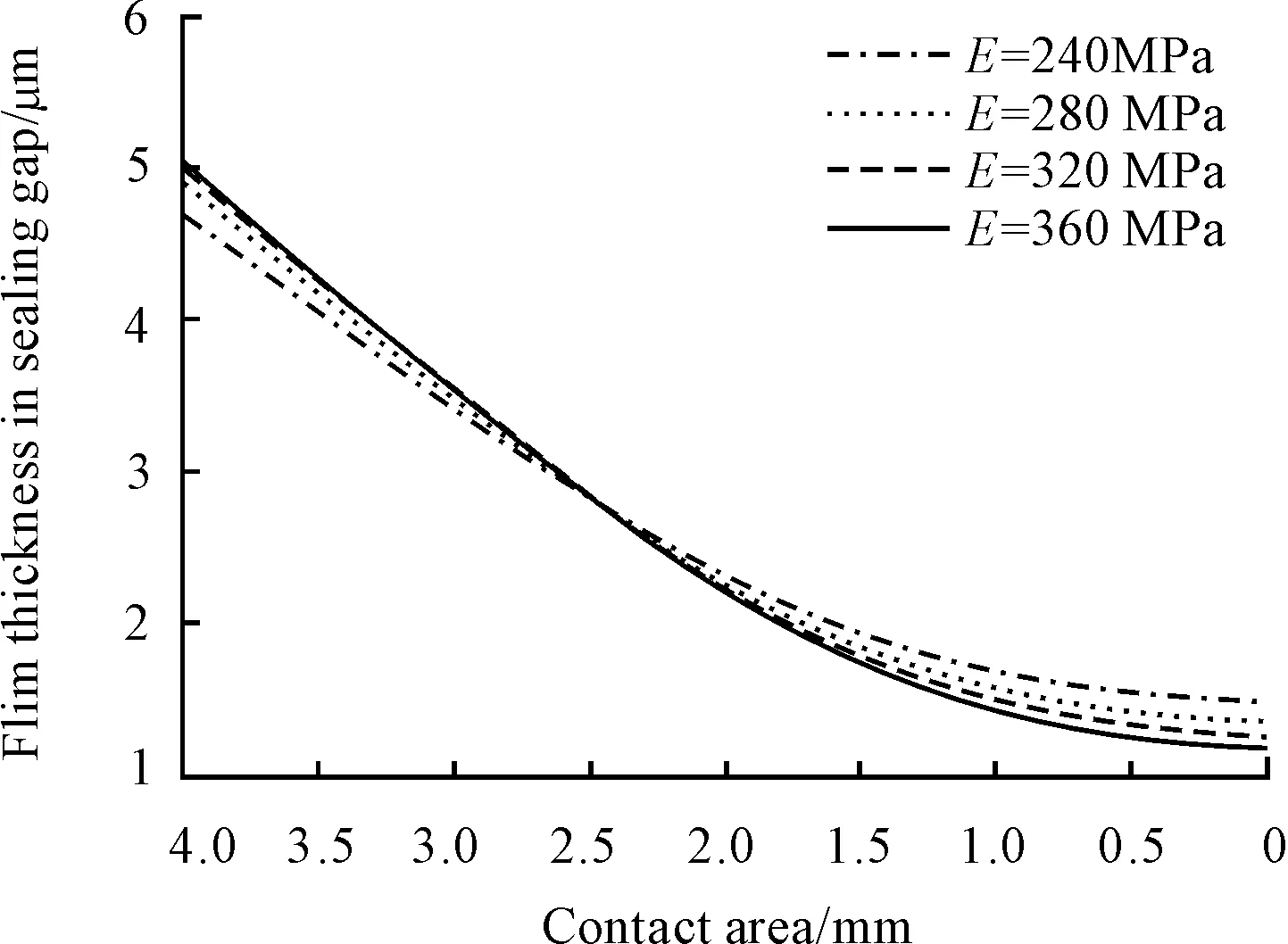
Fig. 9 The film thickness under different elastic modulus
In Fig. 8, the pressure in sealing gap is stable, but it gets higher with the addition of the elastic modulus of the seal. This is because that the contact pressure will grow under the same compression of the seal when the elastic modulus of the seal increases, which leads to the increase of the pressure in sealing gap. Fig. 9 shows that the film thickness at the exist decreased when the elastic modulus of the seal increases, which can reduce the leakage and make the dynamic sealing performance better. In terms of the seal, the elastic modulus is a significant indicator of its physical properties, in the present study, the material of the seal is polytetrafluoroethylene. Thus, the composition and ratio can be adjusted according to the result to get better elastic modulus, which can help obtain better sealing performance.
3.4 The influence of Poisson ratio on film thickness
Setting and remaining the initial compression of the seal, assuming that the sealing pressure is 25 MPa, the relative sliding velocity is 0.1 m/s and the elastic modulus of the seal is 280 MPa, calculating the film thickness at the Poisson ratio 0.38, 0.4, 0.42 and 0.46, the distribution of the pressure and film thickness in sealing gap are shown in Fig.10 and Fig.11.
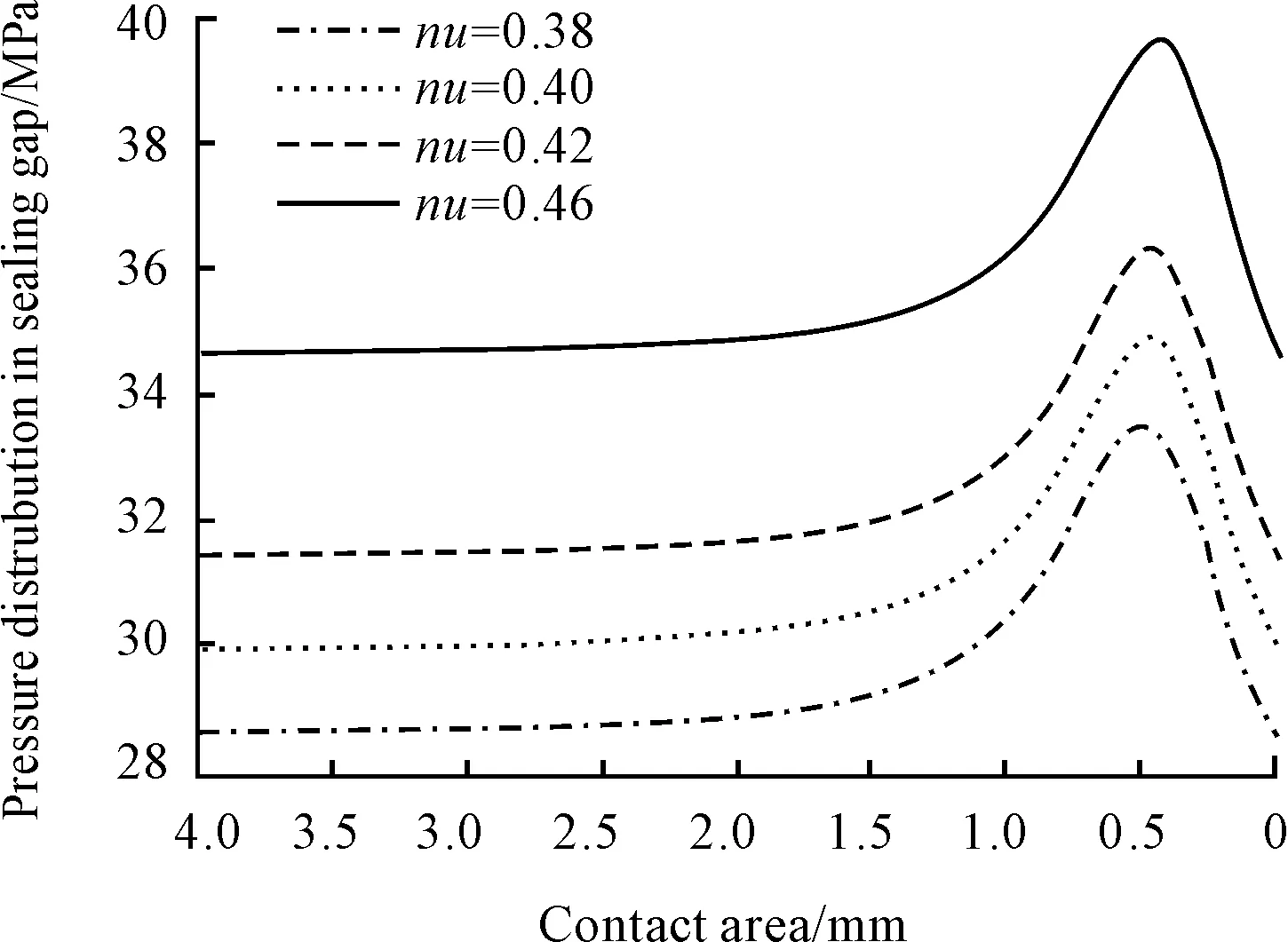
Fig. 10 The distribution of pressure under different Poisson ratio

Fig. 11 The film thickness under different Poisson ratio
In Fig. 10, the distribution of pressure in sealing gap is similar to the one in Fig. 8. Fig. 11 shows that the film thickness at the exist increases with the greater Poisson ratio, which leads to more leakage and is not conducive to dynamic seal. However, the seal’s Poisson ratio changes little, and the physical properties of the seal generally change in a relatively small range. Thus, the physical properties of the seal do not have a significant effect on sealing performance. They can also help to improve sealing performance to some extent.
4 Conclusions
In this paper, the film thickness in sealing gap is calculated through elastic hydrodynamic lubrication and the mechanical deformation in each part of the seal. The mathematical model established takes many parameters into account, which makes the model complex and hard to solve with an analytical method. Therefore, the film thickness is obtained by a numerical method.
This paper mainly discusses the effect of sealing pressure, relative sliding velocity, the elastic modulus and Poisson ratio on the film thickness in sealing gap. According to the analysis results, the film thickness increases with the greater sealing pressure, relative sliding velocity and Poisson ratio, but it will decrease with the increasing elastic modulus of the seal. Meanwhile, sealing pressure and relative sliding velocity has a greater effect on the film thickness, while the elastic modulus and Poisson ratio of the seal affect less. In practical project, the sealing pressure and relative sliding velocity are clearly required. In this case the sealing performance can be improved through making the elastic modulus and Poisson ratio of the seal better.
[1]White C M, Denny D F. The sealing mechanismof flexible packings[J]. MAP Scientific and Technical Memorandum No. 4/45 (interim report), London, UK, 1945.
[2]White C M, Denny D F. The sealing mechanismof flexible packings[J]. Scientific and TechnicalMemorandum No. 3/47, UK Ministry of Supply, 1947.
[3]Dowson D, Swales P D. The development of elastohydrodynamicconditions in a reciprocating seal[C]//In Proceedings of the 4th International Conference on Fluid sealing, 1969: 2-10 (BHRA).
[4]Johnson K L. Contact Mechanics[M]. London and New York: Cambridge University Press, 1985: 53-55.
一种典型液压动密封油膜厚度的研究
廉志刚1*,孙娟娟2,董彦良1
1.哈尔滨工业大学, 哈尔滨150080 2.深圳迈瑞生物医疗电子股份有限公司, 深圳518057
以摆动马达为例,研究了摆动马达叶片与缸套接触处动密封的油膜厚度。针对该处组合式密封结构建立了一个数学模型,通过计算各部分的变形量从而计算出密封间隙的油膜厚度。该数学模型中考虑了密封压力、相对滑行速度以及密封件的物理特性等对油膜厚度的影响,从而为动密封性能的改进提供依据。
聚四氟乙烯; 接触表面位移; 热弹性; 油膜厚度
15 December 2014; revised 15 March 2015;
Zhi-gang LIAN, Postgraduate,
E-mail: lianli8783@163.com
10.3969/j.issn.1001-3881.2015.18.003 Document code: A
TP271.4
accepted 19 May 2015
Hydromechatronics Engineering
http://jdy.qks.cqut.edu.cn
E-mail: jdygcyw@126.com
猜你喜欢
杂志排行
机床与液压的其它文章
- Design and simulation of the hardware in the loop simulation platform for vehicle ACC system
- The design of the hydraulic cylinder test bed based on cartridge valves
- Research on flexible manufacturing system real-time scheduling optimization
- Mathematic modeling method for addendum line of spiral bevel Gear
- Numerical simulation on the aerodynamic performance of ice coating airfoil of wind turbine blade
- Manufacturing of self-lubricating diamond tools with Ni-Cr alloy adding with Ni/C
