基于粒子群优化神经网络自适应控制算法的并联机器人仿真研究
2015-11-03朱龙英陆宝发赫建立
朱龙英,成 磊,郑 帅,陆宝发,赫建立
(1.盐城工学院汽车工程学院,江苏盐城 224051;2.常州大学机械工程学院,江苏常州 213164;3.安徽理工大学 机械工程学院,安徽 淮南 232001;4.江苏大学 机械工程学院,江苏 镇江212013)
基于粒子群优化神经网络自适应控制算法的并联机器人仿真研究
朱龙英1,成 磊2,郑 帅3,陆宝发4,赫建立2
(1.盐城工学院汽车工程学院,江苏盐城 224051;2.常州大学机械工程学院,江苏常州 213164;3.安徽理工大学 机械工程学院,安徽 淮南 232001;4.江苏大学 机械工程学院,江苏 镇江212013)
针对传统控制算法对并联机器人轨迹跟踪精度控制效果不好的问题,提出了一种并联机器人的改进粒子群优化神经网络自适应控制算法,首先对粒子群优化算法进行惯性权重的优化和变异操作的改进,然后用改进的PSO算法优化神经网络的初始权值并进行在线调节PID参数。最后以六自由度并联机器人为研究对象,将传统PID控制与基于改进PSO优化的神经网络自适应控制算法分别进行了仿真实验。仿真结果表明,在快速性和稳定性能上,基于改进PSO优化的神经网络自适应控制算法比单纯的PID控制更加优越,在一定程度上减小了轨迹输出的误差并且提高了轨迹跟踪精度。
并联机器人控制;PSO优化;PID控制;BP神经网络;输出误差;轨迹跟踪精度
0 引言
并联机器人与串联机器人相比具有高刚度、高精度、误差小、承载能力强以及动态响应快等诸多优点而被广泛应用。但作为被控对象,由于并联机器人本身是一个高度非线性、多变量、多参数耦合的复杂系统,使对其精确控制变的尤为困难。因此,并联机器人系统的控制问题成为近年来研究的主要热点之一[1]。
目前,对于并联机器人的控制最常用的是传统PID控制,其结构简单,易于实现,但其控制参数是固定不变的,然而实际工程中需要控制的大多为一些非线性的复杂系统,面对这种环境其控制效果会变的很差甚至不可控[2]。BP神经网络可以实现输入层与输出层之间的任意非线性映射而且具有很强的自学习自适应能力,非常适合控制一些非线性的复杂系统[3]。将传统PID控制与神经网络组合成神经网络自适应控制器,则PID控制鲁棒性好的特点不仅可以继存下来,神经网络的优点又能被融入其中[4]。然而,Rmulhart研究表明,梯度下降的BP算法依赖于初始权值为基础的选择,收敛速度慢,容易陷入局部最优[5]。针对这些缺点,很多学者对其参数进行了优化。文献[6]采用改进粒子群优化的神经网络对电力变压器进行故障诊断,文献[7]用粒子群优化的神经网络对电动汽车SOC进行估算,在动态目标优化问题[8]等实际应用问题也取得了不错的成绩,文献[9]通过对基本模型算法的改进,提高粒子群算法避免进入局部极值的能力,并用仿真实验证明,改进算法比基本PSO算法和惯性权重的PSO算法更好。
本文针对传统控制算法无法对并联机器人轨迹跟踪精度进行精确控制的问题,提出一种改进的PSO优化神经网络自适应控制算法,并以六自由度并联机器人为研究对象将此算法应用于其中,最后通过仿真实验验证其性能。
1 基于神经网络的自适应PID控制
神经网络自适应PID控制器结构如图1所示。控制器由两部分构成:金典增量式数字PID控制器和BP神经网络[10]。
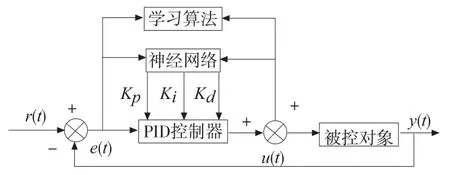
图1 系统结构框图
增量式PID控制率为:
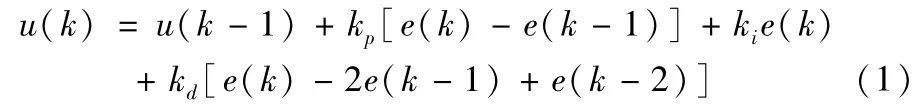
式中,kp、ki、kd为上述PID控制系统的三个可调参数。
三层BP网络结构如图2所示。

图2 BP神经网络结构图
设输入层有节点M个,隐含层节点Q个、3个输出节点。
输入层的网络为:

网络隐含层的输入、输出为:
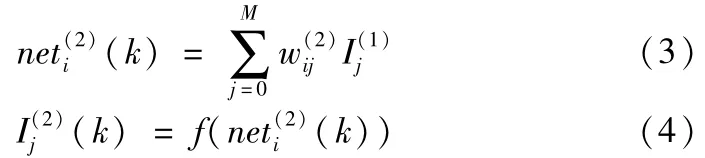
将中间层神经元激活函数进行取双曲正切函数的操作,如下:
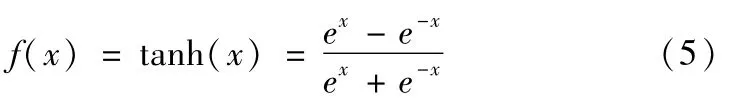
网络输出层的输入、输出为:
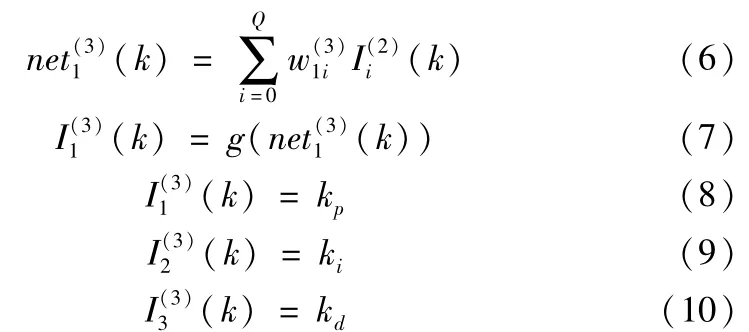
神经网络的3个输出节点分别对应于增量式数字PID控制器的三个可调参数kp、ki、kd,对输出层神经元的激活函数进行取非负的单极性Sigmoid函数的操作:
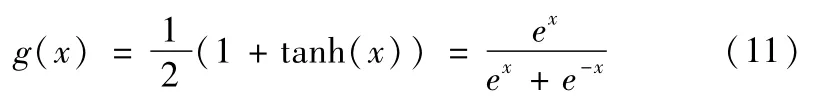
取性能指标函数为:
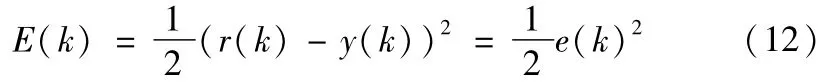
采用神经网络算法修正权系数,同时在权值搜索调整过程中加入惯性项:
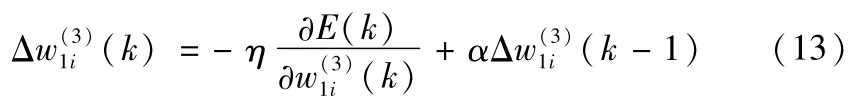
式中,η为学习速率,α为惯性系数。
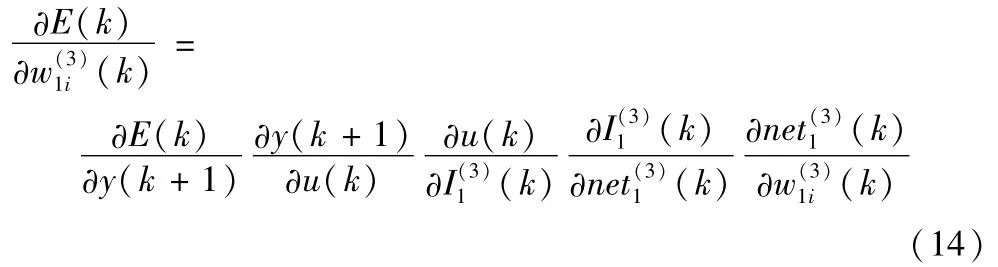
由式(1)可得输出层的学习算法如下式:
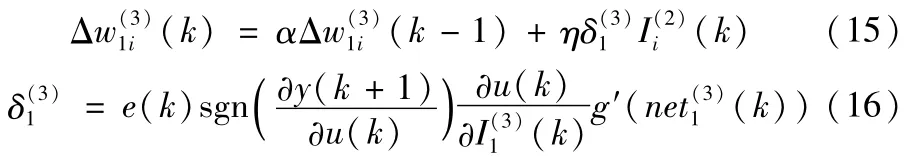
式中,g′(x)=g(x)(1-g(x))。
那么,隐含层加权系数的学习算法如下式:
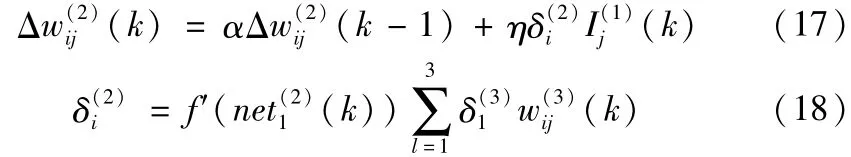
2 改进粒子群优化算法
本文对传统PSO算法进行改进,分别是惯性权重优化和变异操作改进。
2.1 惯性权重的重新调整
为了提高PSO算法的收敛性能,本文对惯性权重w进行了重新调整。实验表明,惯性权重w随着迭代次数的增加而减小,这不仅提高了算法的收敛性能,而且更好地提高了算法的全局和局部搜索能力的目的。
本文提出的自适应惯性权重的调整如下:
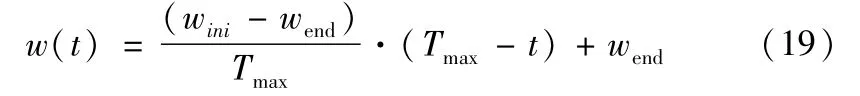
其中,Tmax代表最大的迭代次数;最初的惯性权重为wini;wend代表粒子进化到最大程度时的惯性权重。
根据经验,选取wstart=0.9,wend=0.4时,算法可以表现更好的性能。
2.2 自适应变异操作
本文对粒子群算法加入了自适应变异操作,主要思想是当粒子空间位置每次更新后,可以重新初始化更新的粒子,这样就可以解决原算法在不断迭代的过程中其搜索空间不断减小的问题,使粒子避免进入局部最优。通过加入变异操作使算法的寻优能力变的更为突出。
本文提出的自适应变异操作表达式如下:
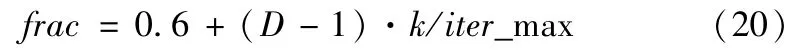
式中,k表示为该时间的迭代次数,iter_max表示为进行的最大迭代数。如果frac>0.9,则令k= ceil(frac),其中ceil函数代表对frac进行正向取整操作,然后再对xik赋一个[-Xmax,Xmax]之间的随机数。
3 改进粒子群优化神经网络自适应控制算法
用改进的粒子群优化算法对神经网络进行优化时,目标函数就是适应度函数[11]。设神经网络的权重为粒子群位置向量X的元素,首先初始化位置向量X,然后用粒子群优化算法搜寻最佳空间位置,这样可以使适应度值取得最小。其表达式为:
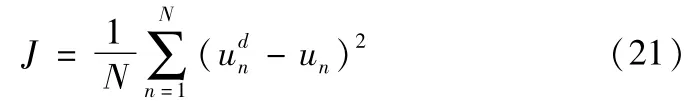
改进的粒子群优化神经网络自适应控制算法由两个部分组成,详细步骤如下:
Step 1:用改进的粒子群优化算法对神经网络的初始权值进行训练。
Step 2:将Step1获得的最佳权值作为神经网络的初始权值,然后用优化后的神经网络进行在线调节PID控制参数。
图3是改进的PSO算法优化神经网络自适应控制算法结构框图。首先,用改进的粒子群优化算法对初始权值进行训练,然后将训练取得的参数代入到神经网络中,最后用神经网络进行在线调节PID参数。
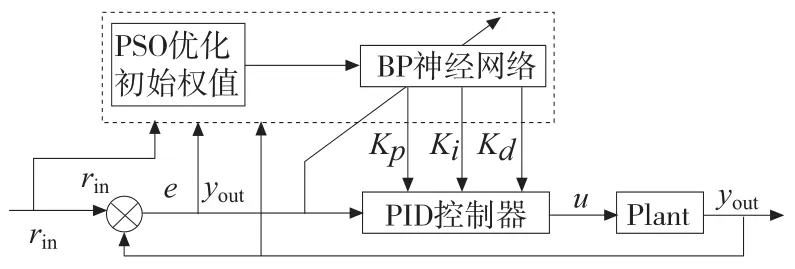
图3 基于粒子群优化的神经网络自适应控制结构图
4 应用实例
4.1 并联机器人模型简介
本文研究的六自由度并联机器人由动平台、静平台和6条结构相同的支链组成,其中上平台为动平台,下平台为静平台,每根驱动杆上下关节分别采用虎克铰与上下平台相连接。机构简图,如图4所示。假设给定并联机器人的结构参数:动平台短边对角θ1= 20°,静平台短边对角θ1=30°;动平台外接圆半径r1=200mm,静平台外接圆半径r1=300mm;当并联机器人处于平衡位置时动平台高度h=440mm;六根驱动杆的最大行程为200mm。
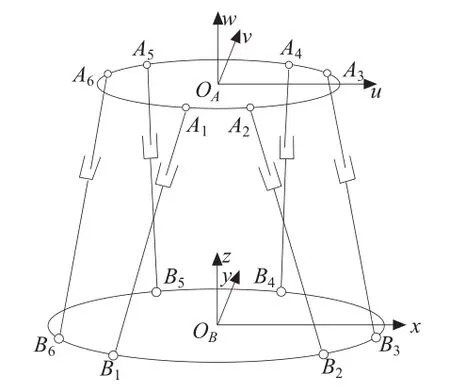
图4 机构简图
本文主要针对当并联机器人为空载的情况下,对并联机器人进行轨迹跟踪控制,假设机器人按照以下给定的轨迹方程进行运动,函数定义如下:
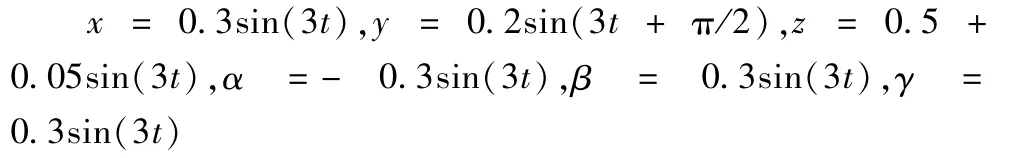
4.2 基于Simulink的并联机器人控制仿真
4.2.1 基于两种控制的并联机器人运动轨迹仿真
图5为当kp=2×105,ki=103kd=-103时,基于传统PID控制下并联机器人动平台中心点沿xyz方向的实际运动轨迹曲线图。
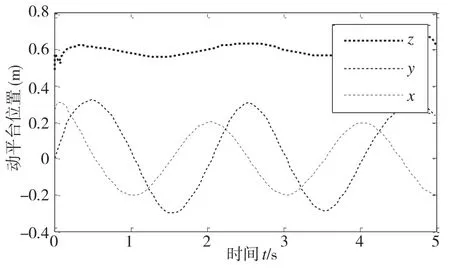
图5 动平台中心点的运动轨迹(PID控制)
本文针对并联机器人模型中的速度进行了简化,并加入基于改进PSO优化的神经网络自适应PID控制器。针对PSO优化算法的关键参数设置为:粒子规模n=25;迭代次数iter_max=100;惯性权重w按式(19)来计算,位置和速度分别限制在[-5,5]和[-1,1]。针对BP算法的参数设置为:网络结构为4-5-3;学习速率η=0.25以及惯性系数α=0.02;输出层的激活函数取单极性Sigmoid函数,取增益A=1,增益B=20,放大增益K=103,图6即为在基于PSO BP PID控制下并联机器人动平台中心点沿xyz方向的实际运动轨迹曲线图。
通过对比两种控制算法对并联机器人轨迹跟踪控制的轨迹曲线可以观察出并联机器人的改进粒子群优化神经网络自适应控制算法比传统PID控制仿真出来的曲线更加平滑稳定,证明本文提出的改进策略优于传统的PID控制。
4.2.2 基于两种控制的并联机器人误差对比分析
以下对并联机器人分别进行传统PID控制和基于改进PSO优化的神经网络自适应PID控制算法分别进行仿真,并对两种控制的仿真结果进行误差对比,其六根驱动杆的控制误差仿真对比如图7所示。通过图中可以准确的观察出并联机器人的改进粒子群优化的神经网络自适应PID控制的稳定性比单纯的PID控制更加优越,在一定程度上减小了轨迹输出的误差并且提高了轨迹跟踪精度。
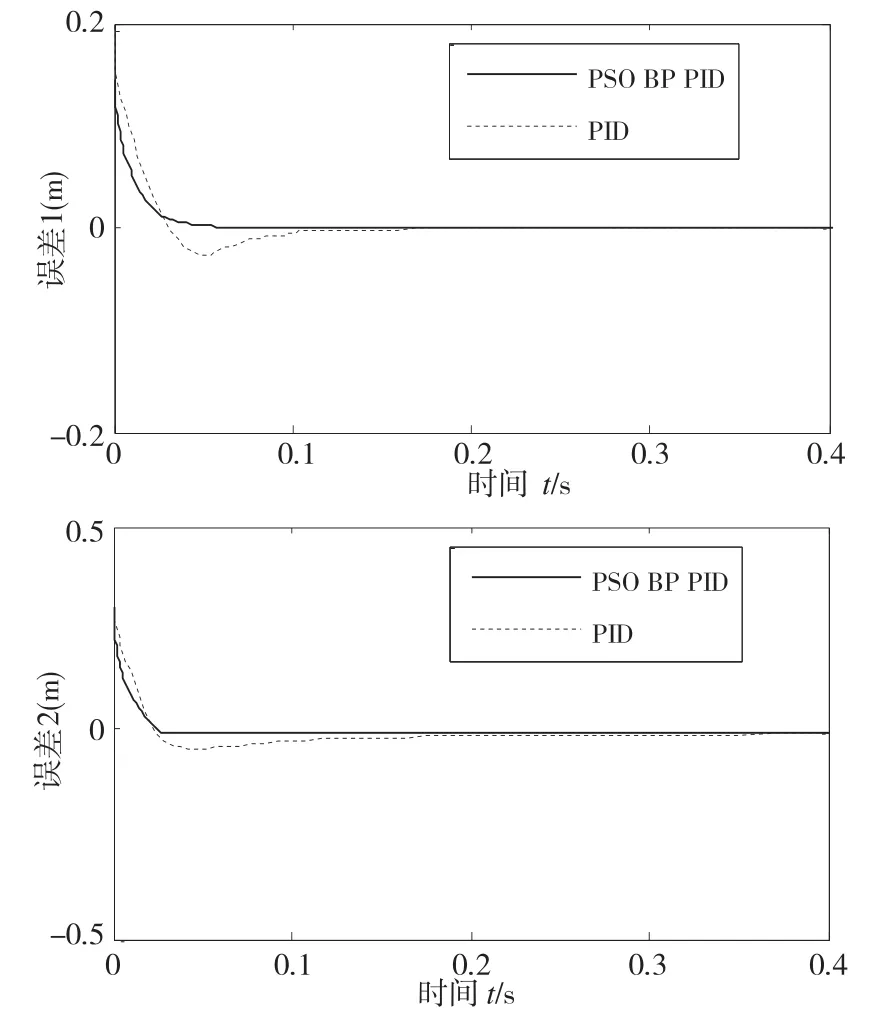
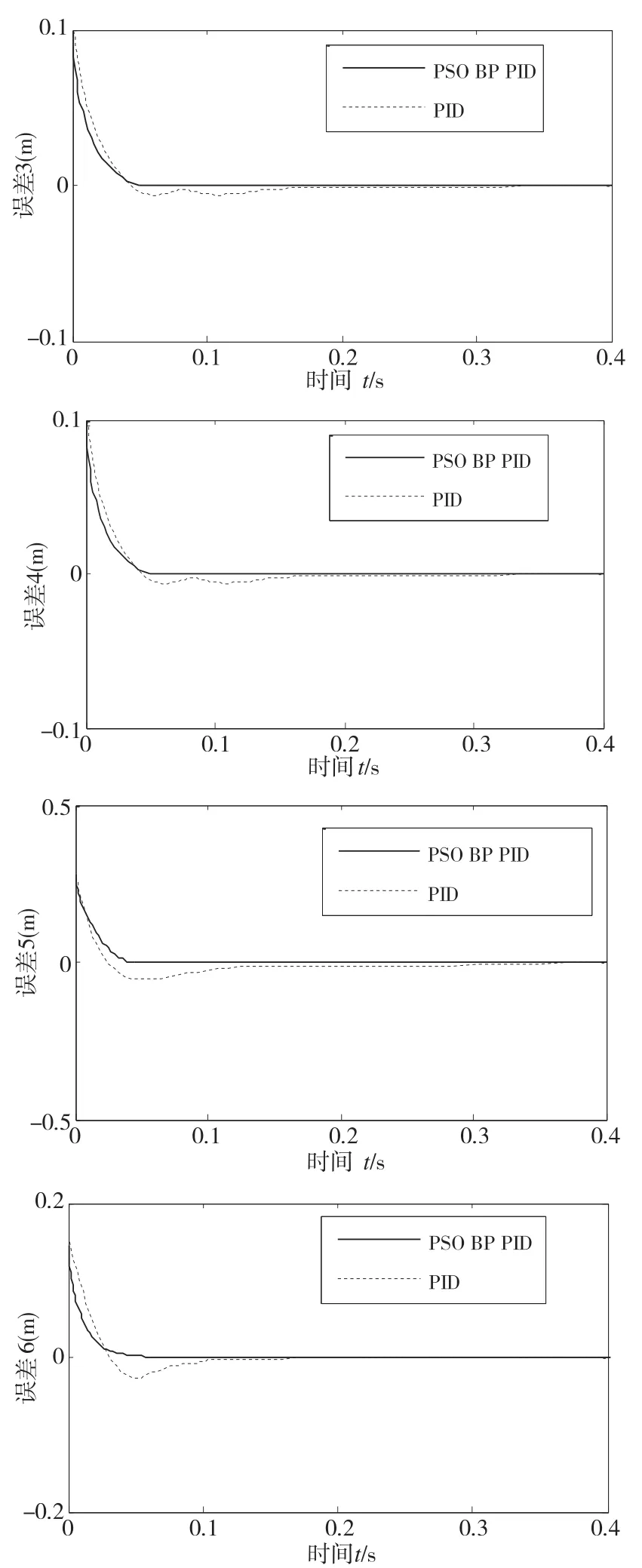
图7 六根驱动杆的控制误差对比图
5 总结
并联机器人的改进粒子群优化神经网络自适应控制算法,解决了传统控制算法对其控制效果不好的问题,并将此控制算法成功的应用到了六自由度并联机器人中,分别用传统PID控制和基于改进PSO优化的神经网络自适应控制算法对机器人进行了轨迹跟踪控制仿真实验,比较了两种控制算法的仿真图形,从仿真结果来看,本文提出的改进算法在性能上远优于传统控制算法,值得推广使用。
[1]刘延斌,张宏敏,赵新华.3-RRRT型并联机器人自适应神经网络滑模控制[J].系统仿真学报,2009,21(11):3398-3400.
[2]高秀兰,鲁开讲,郭旭侠.并联机构非线性PID自适应控制[J].机械设计与制造,2012(12):125-127.[3]昝鹏,颜国正,于莲芝.基于神经网络PID控制的柔性微机器人系统[J].机器人,2007,29(3):219-223.
[4]ZHOU Y,WU X,LIG.Research on PID Controller on BP Neural Networks[J].Journal of Air Force Force Engineering University(Natural Science Edition).2007,4:014.
[5]马兆兴,万秋兰,李洪美,等.基于神经网络的SVC电压稳定性控制[J].电力系统保护与控制,2011,39(18):67-71.
[6]程加堂,熊伟,徐绍坤,等.基于改进粒子群优化神经网络的电力变压器故障诊断[J].高压电器,2012,48(2):42-45.
[7]王业琴,刘一星.粒子群优化神经网络电动汽车SOC估算方法[J].电源技术,2013,37(5):800-803.
[8]赵志刚,张振文,石辉磊.带扰动因子的自适应粒子群优化算法[J].计算机科学,2013,40(12):68-69.
[9]钱雪忠,李静,宋威.改进的粒子群模糊聚类算法[J].计算机工程与应用,2013,49(22):115-118.
[10]Zhang G D,Yang X H,Lu D Q,et al.Research on Pressurizer Pressure Control System Based on BP Neural Network Control of Self-Adjusted PID Parameters[J].Applied Mechanics and Materials,2013,291:2416-2423.
[11]Ying J,Pan H,Dai J.BP network based aeroengine identification using modified particle swarm optimization.Control Conference(CCC),2013 32nd Chinese.IEEE,2013:3321-3325.
The Research of Parallel Robots Simulation Based on Particle Wwarm Optimization Neural Network Adaptive Control Algorithm
ZHU Long-ying1,CHENG Lei2,ZHENG Shuai3,LU Bao-fa4,HE Jian-li2
(1.School of Automotive Engineering,Yancheng Institute of Technology,Yancheng Jiangsu 224051,China;2.School of Mechanical Engineering,Changzhou University,Changzhou Jiangsu 213164,China)
Traditional control algorithm to control the problem of bad effects on trajectory tracking precision of parallel robot,this paper proposes a improved parallel particle swarm optimization neural network robot adaptive control algorithm based on the first PSO algorithm to optimize inertia weight and improved contraction factor,the improved PSO algorithm is then applied to optimize the initial weights of neural network and adjust PID parameters on-line.Finally,a 6-DOF parallel robot is chosen as the study object.The traditional PID control and improved PSO optimize neural network adaptive control algorithm are simulated.Simulation results prove that the performance of improved PSO optimize neural network adaptive control algorithm is far superior to the traditional PID control on the rapidity and stability,and reduce the output trajectory error and improved the trajectory tracking precision to a certain extent.
parallel robot control;PSO optimization;PID control;BP neural network;output trajectory error;trajectory tracking precision
TH166;TG659
A
1001-2265(2015)01-0114-04 DOI:10.13462/j.cnki.mmtamt.2015.01.032
2014-05-04
朱龙英(1962—),女,江苏大丰人,盐城工学院教授,博士,研究生导师,主要从事机器人技术研究,(E-mail)305242634@qq.com。
