球面渐开线齿形的弧齿锥齿轮建模及优化*

李丹红，阿达依·谢尔亚孜旦，丁 撼，冯 广

（新疆大学机械工程学院，乌鲁木齐 830046）

球面渐开线齿形的弧齿锥齿轮建模及优化*

李丹红，阿达依·谢尔亚孜旦，丁 撼，冯 广

（新疆大学机械工程学院，乌鲁木齐 830046）

综合优化以往研究方法的优势和特点，将球面渐开线理论应用于建模中，提出了弧齿锥齿轮球面渐开线齿面的形成原理。从齿面的精确形状出发，利用该理论求导了组成完整齿廓的各部分曲线以及齿线等重要曲线的参数化方程。同时，以扫略创建曲面、从点云创建曲面等CAD曲面设计功能为主体，分别提出了齿轮建模的新方案，即端面齿廓扫略建模、齿面离散点云建模，并就上述方案提出了各自相应优化方法。最后结合算例，表明了其建模及优化方案得到的齿面模型精度高，为弧齿锥齿轮的快速精确建模提供了理论基础和途径。

球面渐开线；弧齿锥齿轮；齿廓曲线；参数化方程；CAD曲面设计功能；快速精确建模

0 引言

弧齿锥齿轮是一种齿面结构很复杂的关键机械动力传动部件，因重合度高具有承载能力强、传动平稳、噪音小等诸多优点［1-2］，被广泛应用于汽车、航空、机床、工程机械等制造工业领域。弧齿锥齿轮的模型设计，为螺旋锥齿轮的数字化制造提供基础，支撑了其中的齿面接触分析（TCA）和齿面误差修正等关键技术，故其一直是研究领域的重点。目前，弧齿锥齿轮的建模研究成果都是以传统的加工方法和齿轮啮合原理为基础，借助三维绘图和数据分析与处理软件完成的齿轮建模，存在着诸多不足，主要表现在建模精度较低：离散点提取过程中存在插值精度误差；忽略了齿廓上的过渡圆角曲面的推导与处理；缺少了仿真加工后齿面的优化与重构；没有进行齿面偏差的测量与修正。

另外，弧齿锥齿轮设计的齿形存在误差，具体表现为：它采用一种近似球面渐开线的齿形，齿轮接触时在齿廓和齿长方向都存在开脱，在任意瞬间为点啮合且接触迹线通过齿面［3］，造成了传动比不稳定啮合不理想的现实问题。而在实际的弧齿锥齿轮传动中，齿廓是为以基锥顶点为球心的球面曲线［4］，并且球面渐开线齿形齿轮副能够弥补近似球面渐开线齿形的不足。因此，本文避开了传统的研究理论和加工方法［5］，利用球面渐开线理论于建模研究中，提出了弧齿锥齿轮球面渐开线齿面形成理论并完成了齿面方程的参数化推导。然后，以计算机辅助设计（CAD）中相关曲面设计功能为准绳，探求了弧齿锥齿轮的多种建模新方案，且一一提出了多种优化方案，以便达到建模的足够精度，同时为弧齿锥齿轮的快速精确参数化建模创造条件。

1 球面渐开线齿面形成理论

如图1所示，借助于球面渐开线理论，弧齿锥齿轮齿面的形成原理可以表述为：当一圆形平面O与基锥面OK0N相切，且在基锥面上做纯滚动时，圆面上的曲线K0Kt在空间轨迹就形成了轮齿的齿面。其中圆面O为发生面，曲线K0N就是发生线，而曲线K0Kt则成为产形线。该产形线上端点K0和Kt所形成的空间轨迹为齿轮大小端的球面渐开线。同时，改变发生面O的半径R和旋转角度θ，就可提供了多种可行的建模方案。其中，球面渐开线K0Kt的方程可用线上任一点K的球面偏角βk表示为［10］：

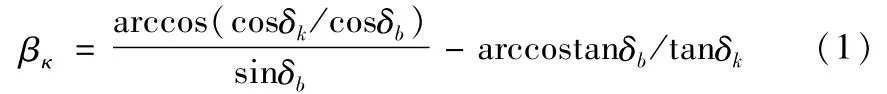
在球面坐标系中，可简化为：

以上各式中，δk为球面渐开线上某点所对应的锥角，δb为基圆锥角。

图1 球面渐开线齿面形成理论图

2 端面齿廓扫掠建模

2.1 球面渐开线齿廓曲线的基本组成

如图2所示，一个完整的球面渐开线弧齿锥齿轮的齿廓至少由四部分组成：S1段齿顶，S2段工作齿廓，S3段齿根，以及连接工作齿廓及齿根的S4段齿根过渡圆角。在弧齿锥齿轮的加工过程中，工作齿廓线所成的曲面由刀具的直线刃部分包络展成，过渡曲线所构成的过渡曲面，根据刀具形状的不同，是由刀具齿顶尖或者齿顶圆角包络形成的。

图2 齿廓曲线的组成

2.2 齿廓曲线各部分的求解

（1）工作齿廓的求解。工作齿廓曲线S2是一段球面渐开线，根据球面渐开线齿面形成理论和推导方程，在齿轮大端可以表示为：

与S2对称一侧的工作齿廓曲线可表示为：

其余参数与S2一致。

（2）齿根和齿顶的求导。齿根曲线S4是齿根圆上的一段圆弧，故可以表示为：

同理，与之对称的一侧齿根曲线为：

其余各参数与与S4一致。而齿顶的求解与齿根类似，只需将根锥角δf变成顶锥角δa，另将根锥齿厚角δfs变成顶锥齿厚角δas即可。

（3）小端齿廓曲线各部分的求解。相对于大端齿廓曲线，小端的齿廓曲线只是矢径ρ和转角φ发生了变化，其参数化方程可表示为：

上式中，B为齿宽。

2.3 齿廓曲线的形成

根据齿廓曲线的基本组成，其工作齿廓曲线为球面渐开线，故其可由球面渐开线齿面形成理论求解。在三维绘图软件中绘制并装配好相切的发生面与基锥模型，利用旋转功能，模拟大端面端点K0和Kt的空间运动轨迹就可得出其大小端面完整的端面齿廓曲线。

至于齿顶和齿根，由于是齿顶圆和齿根圆上的一段圆弧，可以根据相关参数方程直接绘制。而连接工作齿廓和齿根的过渡圆角曲线，其绘图时则需要通过倒角圆方法进行处理：

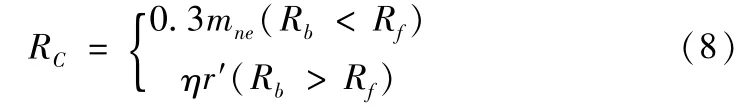
式中，mne为法向模数，Rb为基圆锥半径，Rf为齿根圆半径，r′为最大刀尖圆角半径，系数η≥1。

2.4 引导线的方程求解

弧齿锥齿轮的节锥与齿面的交线称为节线，其表示了齿轮的纵向齿形。在平面内，齿轮的节线称为齿线，真实的反映了齿轮的弧线形状，故可以作为引导线。图3表示了弧齿锥齿轮的齿线，其中左图表示了加工状态时齿线形成过程，而右图是其几何示意图。令r0为刀盘半径，点O到O1表示刀位，β为名义螺旋角，可用节线上任意一点的螺旋角β′和锥距R′来表示齿线方程：

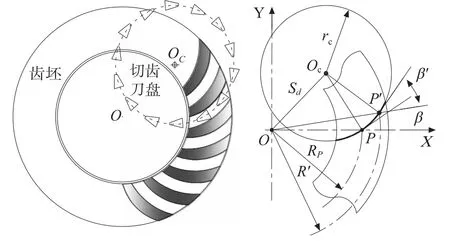
图3 弧齿锥齿轮的齿线

2.5 端面齿廓扫掠建模及优化方案

如图4所示，在绘图软件（如pro/E、UG）中，根据已经求导的参数化方程，由端面齿轮廓曲线的沿齿线方向的扫掠就可完成建模，大致有以下几个步骤：①创建齿轮的基锥。②构造大小端的齿廓曲线。③绘制引导线。④进行扫掠和阵列操作，前者完成单个齿面，后者完成所有齿面的模型。

图4 端面齿廓曲线扫描建模

为了保证模型设计的足够精度，在该种建模方法的基础上可以作如下改进。

（1）截面齿廓曲线串插值。在已经求导的大小端齿廓之间，以齿线为参考基准，可等值改变矢径ρ变化量，使其在齿线方向上存在若干等距离的齿廓曲线，参数改变为：

上式中，ΔL为每次插值的距离改变量，可适当取值，t为所插入曲线的数目。

（2）适当增加引导线。例如在图5中，齿面上一侧齿顶线a和b的求解，可看作是沿齿线点的转动，可表示为：

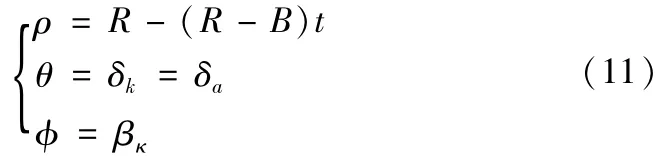
同理，根据过渡圆角和齿根圆的起始点坐标，通过改变矢径ρ的变化量，依次可以求出齿面上相应的齿根圆角线c和d、齿根线e。

图5 添加的引导曲线

3 齿面离散点云建模

3.1 弧齿锥齿轮齿面离散点的求取

基于相关的参数化方程等份求取齿面的U线和V线的方程，然后联立二者方程求取交点，就可以得出齿面网格曲线及其交点构成的均匀分布的离散点。如图6所示，将齿面选取了7×7个均匀分布的离散点，其中U线和V线都是7条。

（1）U线的参数方程。在求取的产形线上根据Rn变化值获取均匀的N等分点，其中，取N等分点可以由以下公式确定：

根据求取的齿廓曲线参数化方程，求取各点在形成齿面的过程中的运动轨迹即为U线的方程表达式。

（2）V线的参数方程。根据以求的端面齿廓中齿面部分的参数化方程，可同样等值等距获取N等分点，然后只需适当改变矢径ρ，即：

就可以快速得到齿长方向的一组等距曲线即为V线的参数方程表达式。

（3）离散点的求取。联立U线和V线的参数方程组，得出其交点的参数方程，然后可输入一些数据处理软件（如MATLAB、CAXA）等，进行齿面离散点信息的求取并输出点的数据，构成一个后缀为“.dat”文件。

图6 齿面离散点的求取与边界

3.2 相关设置及齿面离散点云的边界求解

在创建齿面的过程中，U向和V向阶次可以适当选取，一般选取三次或三次以下的曲线表达式，而补片类型可选单个，沿U向和V向封闭。另外，齿面点云的边界是一个重要环节，可以通过如下方式获得：如图6所示，齿面边界其实就是齿面与大端面、小端面、顶锥面、根锥面等四个面的相交线，而这四条边界曲线可以根据已经求得的参数方程依次求得。

3.3 齿面离散点云建模及优化方法

齿面离散点云创建齿面的建模过程大致为：先通过读取齿面离散点的数据文件获取点信息依次创建出组齿面各个片体，利用缝合技术完成单个齿面的创建，然后利用相关参数快速创建齿坯模型，最后通过单个齿面与齿坯的布尔运算得出单齿，再通过阵列就可完成整个弧齿锥齿轮的建模。为了进一步提高建模的精度，可以通过如下方法进行改进：

（1）完成一体化整个轮齿的齿面离散点求取和建模。点的求取范围不只仅仅包括轮齿凹面或凸面的离散点，而是将齿顶面、齿根面、凹凸面、大小端面一起作为单个齿面载体，根据已经求解的精确方程，完成一体化的均匀分布整个轮齿的离散点信息的提取。这样，减少了各部分齿面的反复提取过程和缝合，提高了效率；也避免了曲面片缝合过程中和数据多次处理中的累积误差，提高了精度。

（2）进行非均匀有理B样条（NURBS）齿面重构处理。在得到齿面模型后，可以利用NURBS蒙皮技术完成齿面重构，然后利用能量法或者小波分析进行光顺处理，以进一步优化齿面，提高齿面的光顺度和精度。很显然，根据齿面离散点求取过程中的U线和V线构成齿面交线网格，可以构成一个NURBS曲面。其中，由U向和V向的两个参数变量（u，v）可以形成分段有理多项式，故其NURBS曲面可以定义为：

4 算例

根据球面渐开线齿面形成理论和CAD曲面设计功能，本文给出了由齿面离散点云建模及优化方案所得出的算例。如图7所示，左图是弧齿锥齿轮的模型，右图是利用NURBS方法［8］重构的一侧齿面，并通过齿面分析得出的高斯云图可以看出，其齿面光顺性好，精度高。另外，利用齿面一系列均匀分布的离散点与理论点值的一一作数值比较，求解出最终的各个方案的建模精度。如图8所示，三种建模都具足够高的建模精度，其中最大的齿面误差为0.00713mm，最小的为0.00434mm，而三种建模方案的平均误差为0.00546mm，0.00603mm，0.00529mm，大大提高了齿面建模精度。

图7 齿轮模型和齿面NURBS重构及高斯云图

图8 三种建模及优化方案的建模精度比较

5 结论

本文提出的球面渐开线齿面形成理论，更加简单快捷，且实用性强。尤其是以CAD曲面设计功能为主进行建模，是对以往的研究方法取长补短并推陈出新，减少了以前繁杂绘图和大量计算的时间。通过球面渐开线齿面形成理论，能快速精确的完成齿面方程的显示表达，并能通过NURBS等方法进行优化和处理，大大提高了建模的精度，也为弧齿锥齿轮参数化和多元化设计提供途径。另外，这些建模方案为更广泛的弧齿锥齿轮加工创造了条件。首先，利用该形成原理将产形线作为刀盘刀刃与工件齿坯做切齿运动，完成球面渐开线的空间运动可切出齿面完成轮齿加工，在此方面有吉林大学的科研团队开始实验研究并以得了成果。其次，其精确地参数化齿轮模型为齿面接触分析（TCA）等数字化加工关键技术提供有效的齿面信息。另外，其NURBS齿面重构中的齿面离散点所在的曲线网格，还可为通用机床的锥齿轮数控加工乃至NURBS加工中刀具路径计算和规划提供基础。

［1］Litvin F L，Wang A G，Handschuh.Computerized generation and simulation of meshing and contact of spiral bevel gears with improved geometry［J］.Comput.Methods Appl. Mech.Engrg.1998，158：35-64.

［2］Faydor L.Ltivin，Alfonso Fuentes，Qi Fan，et al.Computerized design，simulation of meshing，and contact and stress analysis of face-milled format generated spiral bevel gears［J］.Mechanism and Machine Theory2002，21：775-786.

［3］张学成，呼咏，杨兆军.基于齿面发生线的弧齿锥齿轮切齿运动分析［J］.北京工业大学学报，2008，36（11）：1441-1446.

［4］曾韬.螺旋锥齿轮设计与加工［M］.哈尔滨：哈尔滨工业大学出版社，1989.

［5］Litvin F L.Gear Geometry and Applied Theory［M］.USA：Cambridge University Press，2004.

［6］张鸿源.圆锥齿轮测量［M］.北京：中国计量出版社，1988.

［7］朱孝录.齿轮传动设计手册［M］.北京：化学工业出版社，2005.

［8］孙玉文，刘宏军，刘健.基于NURBS的自由曲面精确拟合方法研究［J］.机械工程学报，2005，40（3）：10-14.

［9］李敬财.螺旋锥齿轮数字化制造基础应用技术的研究［D］.天津：天津大学，2008.

［10］Qi Fan，Ron Dafoe.Gleason expert manufacturing system（GEMS）open a new era for digitized manufacturing of spiral bevel gears［J］.World manufacturing engineering&market，2005（4）：87-93.

（编辑 李秀敏）

其中，pij是控制网格上的顶点即交点，wij是顶点的权因子，Ni，ku（u）是在交点区间内的第i个ku次样条基函数，Nj，kv（v）是在交点区间内的第j个kv次样条基函数。

Modeling and Optimizations of the Spherical Involute Tooth Profile for the Spiral Bevel Gears

LI Dan-hong，ADAYI·Xieeryazidan，DING Han，FENG Guang
（School of Mechanical Engineering，Xinjiang University，Urumqi833046，China）

Principle of forming spherical involute tooth surface about the spiral bevel gear was proposed with the application of the spherical involute theory in the modeling，on the basis of comprehensive optimization of advantage and characteristics of previous research methods.From a complete tooth profile curve，the quick and accurate derivations of basic parametric equation of each part of the tooth profile curve were made by the principle.Besides，the important tooth line were done.At the same time，on the base of some CAD features about sculptured surface namely by sweeping to found surfaces，and creating a surface from the point cloud，some new approaches were correspondingly proposed，which were sweeping from tooth profile，and discrete point cloud on the tooth surface.And it accordingly made optimization methods for the program proposed.At last，through the given examples，these approaches have been proven that gear model have high accuracy，fast efficiency that can provide some theoretical foundation and means for fast and accurate modeling of spiral bevel gears.

the spherical involute；spiral bevel gears；tooth profile curve；parametric equations；CAD features about sculptured surface；fast and accurate modeling

TH122；TG506

A

1001-2265（2015）01-0009-04 DOI：10.13462/j.cnki.mmtamt.2015.01.003

2013-12-07；

2014-05-09

国家自然科学基金资助项目（50965017）

李丹红（1990—），女，新疆昌吉人，新疆大学硕士研究生，研究方向为CAD/CAM及先进制造技术，（E-mail）1561179874@qq.com；通讯作者：阿达依·谢尔亚孜旦（1963—），男，新疆阿勒泰人，新疆大学教授，研究方向为特种加工、先进设计及制造技术方法，（E-mail）adayxj@126.com。