永磁同步电机的时间尺度自抗扰控制参数整定
2015-11-03刘小斌赵洛印
刘小斌,张 旭,赵洛印
(东北石油大学电气信息工程学院,黑龙江大庆 163318)
永磁同步电机的时间尺度自抗扰控制参数整定
刘小斌,张 旭,赵洛印
(东北石油大学电气信息工程学院,黑龙江大庆 163318)
针对永磁同步电机(PMSM)复杂、强耦合的非线性特点,同时传统PI控制算法控制精度不高、响应速度慢等特点,提出了一种基于时间尺度参数整定的自抗扰控制(ADRC)PMSM控制策略。在传统的ADRC的基础上分析时间尺度研究参数整定问题,理论分析后得出PMSM的时间尺度,结合时间尺度与ADRC参数的关系进行参数整定。仿真结果表明,该方法在ADRC控制下有良好的动态性能并且对不同的PMSM均具有良好的鲁棒性和抗干扰能力。
永磁同步电机;自抗扰控制;参数整定;时间尺度;MATLAB仿真
0 引言
近些年,新型永磁材料被开发并深度用于电力电子技术的发展,尤其在工生产中的应用极为广泛,集成了新型永磁材料和先进控制技术的永磁同步电机调整系统就是最好的研究成果,永磁同步电机的优点明显,不但利用较小的体积产生较大的转矩外,而且其简单的机械结构和简便的
维护方法更是倍受多个高精尖领域的推广及应用[1]。
以往永磁同步电机的调速方式使用PI[2]控制器来实现,参数易于调整和相对简单的结构特点使得它被广泛的应用。但对不确定性时变多变量关联的非线性复杂系统更是不能达到期望值。因此,在工程控制中智能优化控制器算法受到广泛重视。
本文采取结合时间尺度与自抗扰控制的方法[3],通过MATLAB建立PMSM自抗扰控制系统模型,仿真结果表明ADRC在速度、精确性、抗干扰能力上相对传统PI控制有更好的动态性能,同时对于不同电机在结合时间尺度与自抗扰的条件下可以快速准确的对永磁同步电机进行调速。
1 ADRC数学模型
ADRC由跟踪-微分器(TD)、扩张状态观测器(ESO)和非线性状态反馈控制率(NLSEF)三部分组成[4-5]。对于二阶ADRC原理图如图1所示。

图1 二阶ADRC原理图
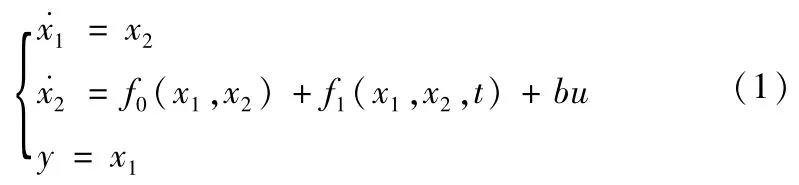
式中:b为系统控制量增益;u为系统控制量;f0(x1,x2)为系统已知部分;f1(x1,x2,t)系统未知部分。
跟踪-微分器数学模型为:

扩张状态观测器:
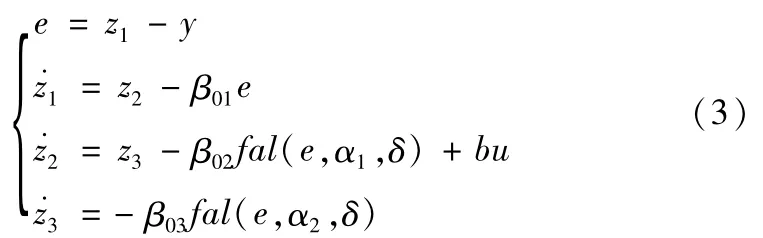
非线性状态误差反馈:
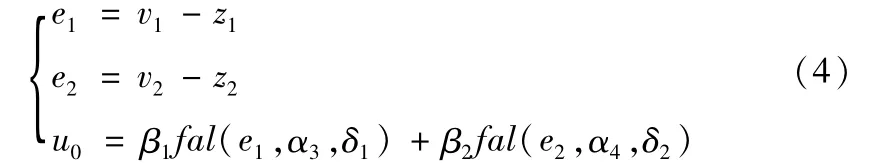
fal(e,a,δ)的函数表达式为:

式中:v为ADRC的给定信号;v1为v的跟踪信号;r为跟踪速度因子;y为被动对象的输出;z2为y的跟踪信号;z3为ω(t)的跟踪值;β01,β02,β03为输出误差校正增益;fal(e,α,δ)为最优综合控制函数;δ表示滤波因子;α为非线性因子;β1,β2为误差增益。
不过谁曾想,25年前,当时华西医院各项指标比较落后,其床位使用率、手术量、门诊量等数据,和成都市的一家市级医院相比并无太大优势。
由于自抗扰控制存在许多参数[6-7],故参数整定成为了不可或缺的部分,本文采用结合时间尺度与自抗扰控制的方法,此方法只需一组已整定好的自抗扰参数就可以对多台电机进行参数整定,既可以快速的计算出各个参数值同时也提高了自抗扰控制的精度。
2 PMSM的时间尺度ADRC参数整定
永磁同步电机构成的调速系统中[8],在旋转(d,q)坐标系中,q轴电流和转速的状态方程为:

式中:Np为极对数,iq为定子电流q轴分量,ψλ为定子磁链,TL为负载转矩,J为转动惯量,B为摩擦系数,R定子电阻,L为d和q轴自感。
将式(6)带入(7)整理可得
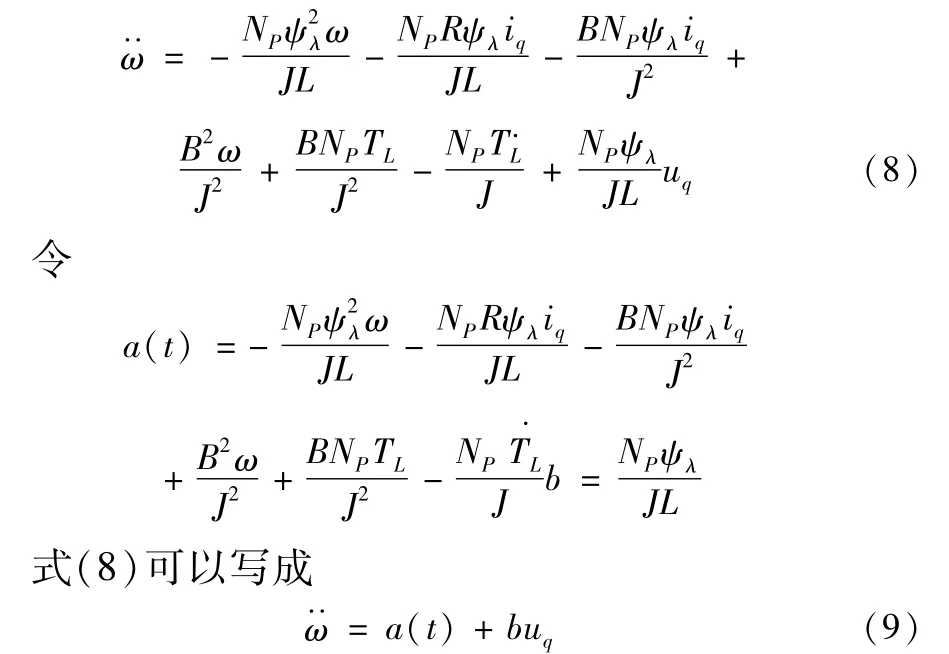
为了抑制负载扰动带来的干扰,结合自抗扰控制器中的扩张状态观测器的特点,将负载扰动归为未知扰动,即可以有效的控制外因的影响。
2.1 PM SM的时间尺度的推导
对于二阶系统[9],记,其中q1,q2为系统工作范围的适当常数,系统的时间尺度为

鉴于ADRC良好的抗扰性,将负载变化归到未知扰动中进行补偿,可有效的抑制负载变化带来的影响,故此处不考虑负载变化,即TL=0。

记极值

其中ω∈[0,n0],n0为额定转速的幅值。
当(k1ψλ-k2)≤0时,化简可知,最大值为0,此时ω=0。
当(k1ψλ-k2)>0时,化简可知,(k1ψλ-k2)ω最大值为(k1ψλ-k2)n0,此时ω=n0

这样就可以根据永磁同步电机的参数算出时间尺度p。
2.2 时间尺度的ADRC参数整定
用U=r0,β01,β02,β03,b0,K0,β0代替ADRC控制器中的参数[10],若已整定好时间尺度为p1的闭环系统的ADRC参数为r1,β11,β12,β13,b1,K1,β1,若跟踪速度因子r0不小于给整定定值r1,同时b1和b0相差不大且关系式≥成立,那么基于时间尺度为p0下的ADRC参数关系如式(14)所示:

根据(13)式可以得到PMSM时间尺度,将一组已调好的ADRC参数和得到的时间尺度带入(14)式中,即可算出此电机自抗扰控制器的各个参数,完成参数整定。
3 仿真结果及分析
在Matlab/Simulink中搭建ADRC的控制系统仿真模型如图2所示。

图2 基于ADRC永磁同步电机转速控制仿真模型
为了验证所提出的ADRC算法和基于时间尺度的ADRC参数整定方法,分别采用PI控制和两台不同型号永磁同步电机进行仿真。第一台电机的额定参数为380V,1.5A,1500r/min,50Hz;电机定子电阻12.9Ω,定子电感0.01H,永磁体磁链0.66Wb,转动惯量8× 10-4kg·m2,阻尼系数0.05,极对数为2。
系统空载启动,0.3s时加入负载转矩,在PI控制器下转速如图3所示。
在相同型号的电机下,采用ADRC,计算得M= 6424938,时间尺度P=1/2535。已整定好的自抗扰控制器参数如表1所示。
系统空载启动,0.3s时加入负载转矩,在ADRC控制器下转速如图4所示。

表1 已整定自抗扰控制器参数
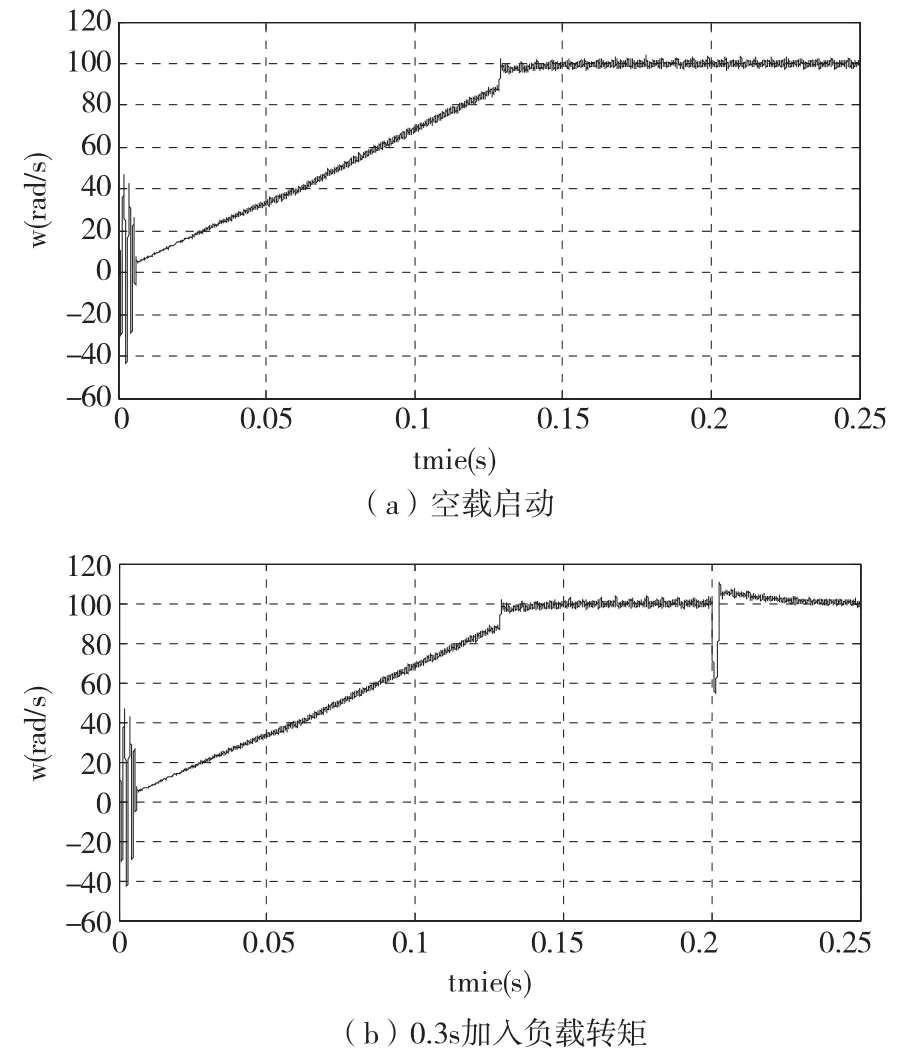
图3 PI控制器作用下速度响应曲线

图4 ADRC控制器作用下速度响应曲线
第二台为额定参数为380V,1.5A,1000r/min,50Hz;电机定子电阻1.9Ω,定子电感0.01H,永磁体磁链0.353Wb,转动惯量7.24×10-4kg·m2,阻尼系数0.01,极对数为2。
计算得M1=1832597,时间尺度P1=1/1354。令m=p/p1=0.53,根据自抗扰参数整定原则可以直接得到控制参数。第二台自抗扰控制器参数如表2所示。

表2 第二台时间尺度整定自抗扰控制器参数
系统空载启动,0.3s时加入负载转矩,在ADRC下第二台电机转速如图5所示。
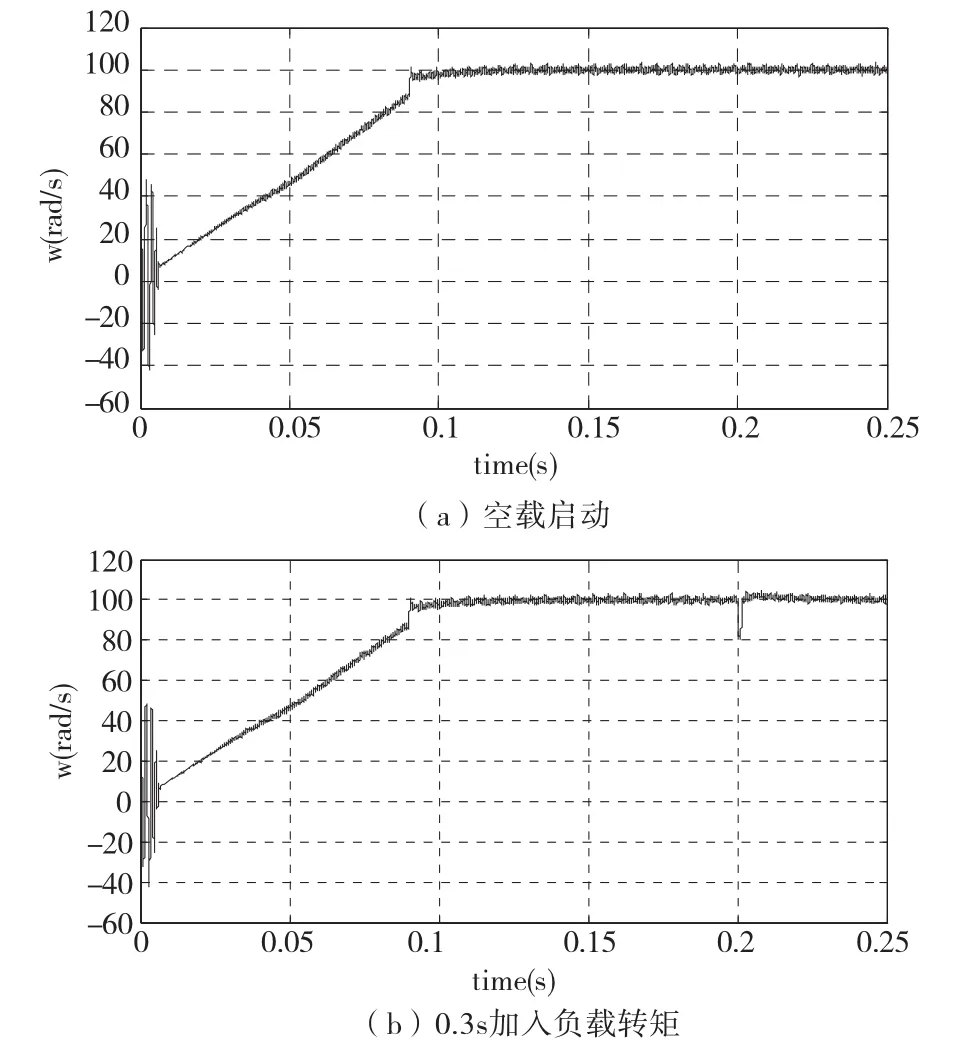
图5 时间尺度参数整定的ADRC速度响应曲线
由仿真结果可以看出,ADRC相对于PI控制的动态性能表现有较小的超调量以及较短的超调时间,在0.3s加入负载时ADRC有较强的稳定性和抗干扰能力。对于不同永磁同步电机通过时间尺度的计算可以高效的得出ADRC的各个参数,避免了传统方法试凑的繁琐以及不确定性因素。
4 结论
本文针对传统PI控制器在永磁同步电机复杂的强耦合非线性的系统下控制精度低反应时间慢的情况,采用二阶ADRC控制器进行转速控制,并结合时间尺度与自抗扰控制器的关系,提出永磁同步电机的自抗扰控制去的整定方法。仿真结果验证了该控制系统转速响应迅速且超调量小具有良好的抗扰动性,整定方法简单高效,此方法可以广泛的应用与永磁同步电机控制系统中。
[1]王礼鹏,张化光,刘秀翀.永磁同步电动机无速度传感器矢量调速系统的积分反步控制[J].控制理论与应用,2012,29(2):199-204.
[2]韩京清.从PID技术到自抗扰控制技术[J].控制工程,2002,9(3):13-18.
[3]侯利民,任志玲,王巍.基于自抗扰控制的永磁同步电机无源调速系统[J].电力电子技术,2011,45(3):37-39.
[4]刘丽英,许镇琳,梅强.基于线性自抗扰控制器的异步电机调速系统[J].组合机床与自动化加工技术,2009(5):56-60.
[5]纪恩庆,肖维荣.二阶自抗扰控制器的参数简化[J].自动化仪表,2007,28(5):27-28,31.
[6]杨巧玲,郝晓弘,张海平.无刷直流电机的新型控制器[J].自动化仪表,2008,29(9):13-15.
[7]张金利,张玉瑞,税冬东,等.永磁同步电机变频调速系统建模与仿真[J].电力电子技术,2008,42(2):67-69.
[8]刘鸣,邵诚.异步电动机的自抗扰控制器及其参数整定[J].控制与决策,2003,18(5):540-544.
[9]白晶,李华德,郝智红.自抗扰控制器ADRC实现的感应电机变频调速系统[J].电工技术学报,2005,20(6):73-76.
[10]李述清,张胜修,刘毅男,等.根据系统时间尺度整定自抗扰控制器参数[J].控制理论与应用,2012,29(1):125-129.
(编辑 李秀敏)
Based on Time Scale Parameter Tuning of Active Disturbance Rejection Control for PMSM
LIU Xiao-bin,ZHANG Xu,ZHAO Luo-yin
(School of Electric Information Engineering,Northeast Petroleum University,Daqing Heilongjiang 163318,China)
According to the permanent magnet synchronous motor(PMSM)complicated,strongly coupled,nonlinear characteristics,to overcome the accuracy is not high and slow response characteristics of the traditional PI control algorithm,given a time scale based on tuning active disturbance rejective control(ADRC)PMSM control strategy.In this paper,based on the traditional ADRC starting from the concept of time scale analysis of the parameter tuning problem,derived from theoretical analysis of PMSM time scales,combined with the relationship between the time scale and ADRC parameters to parameter tuning.The simulation results show that the method under the control of the ADRC has good dynamic performance of PMSM with concurrently on different good robustness and anti-disturbance capabilities.
permanent magnet synchronous motor(PMSM);active disturbance rejective control(ADRC);parameter tuning;time scale;MATLAB simulation
TH166;TG659
A
1001-2265(2015)01-0084-03 DOI:10.13462/j.cnki.mmtamt.2015.01.023
2014-05-05;
2014-06-10
刘小斌(1979—),女,黑龙江讷河人,东北石油大学副教授,硕士,研究方向为电力电子与电气传动,(E-mail)liuxiaobin79@163.com;通讯作者:张旭(1989—)女,黑龙江大庆人,东北石油大学硕士研究生,研究方向控制理论与控制工程,(E-mail)whatever_1025@163. com。
