非正交五轴数控机床旋转轴误差辨识方法的研究*
2015-11-03范晋伟王志远唐宇航
范晋伟,王志远,唐宇航
(北京工业大学机电学院,北京 100024)
非正交五轴数控机床旋转轴误差辨识方法的研究*
范晋伟,王志远,唐宇航
(北京工业大学机电学院,北京 100024)
针对国内外对于非正交数控机床的斜摆轴B轴误差辨识研究较少问题,基于多体系统理论建立非正交五轴数控机床运动误差模型,此模型包含了旋转轴B轴的共计12项静态误差和动态误差,在对此运动误差模型进行数学表达与分析后,结合Renishaw公司的QC10球杆仪测量方式设计了8种不同测量模式。最后结合测量结果可实现斜摆轴B轴的12项误差辨识,快速高效。经试验验证,这种辨识方法测量结果精确,可用于非正交五轴数控机床旋转轴误差辨识。
非正交五轴数控机床;斜摆轴;多体系统;旋转轴几何误差;辨识方法
0 引言
随着数控技术的发展,多轴数控加工中心正在得到越来越为广泛的应用[1]。五轴数控加工中心通常用于加工模具、机械零件与复杂形状以及飞机部件和涡轮叶片[2]。然而,机床误差(如几何误差、载荷误差、热误差)也不可避免地随着加工轴数量的增多而增多[3]。其中,几何误差在整个机床运行时间内都在影响定位精度[4]。按照常规分类,几何误差分为位置相关几何误差和位置无关的几何误差[5]。在实际工况中,机床的各个运动轴存在的几何误差会直接导致机床在加工过程中出现定位误差进而出现加工误差。因此全面准确辨识机床旋转轴的几何误差是实现机床精加工的必要条件。对于五轴数控机床,它的线性轴检测方法已比较成熟和完善[6],目前国内外研究回转轴误差辨识主要针对TTTRR型和RRTTT型机床,且大多数都是正交系列的旋转轴误差辨识[7-9],而对于非正交五轴数控机床的斜摆轴B轴几何误差辨识研究很少,有待加强。
1 旋转轴误差参数
如图1,DMP60U型非正交五轴数控机床的2个旋转轴分别为B轴和C轴。其中单摆头旋转轴B轴与机床坐标系的Z轴存在45°夹角。为研究方便,将基坐标系即体1坐标系选在Y向移动台的零点位置,且取基坐标系的Y轴方向与Y向移动台的理想运动方向一致。取体2、3、4、5的理想坐标系均与基坐标系重合,体6的理想坐标原点系取在B轴轴线与结合面的交点处,方向与基坐标系绕其x轴旋转+45°后一致。刀具坐标系原点选在主轴与端面交点处,方向与基坐标系一致。

图1 DMU60P型五轴数控机床
根据物体空间运动自由度可知,每个旋转轴会产生6项静态误差和对应的6项动态误差,如表1,为书写方便用b1~b6代替这6项位置误差。用bb1~bb6代替对应的6项运动误差。

表1 B轴相关的12项误差项
2 旋转轴误差测量与辨识
2.1 X方向测量模式
如图2,布置X方向测量模式一,布置完成后启动B轴,通过机床多轴联动功能,保持在理想情况下刀具一端的小球在工作台坐标系O中的实时位置保持不变。根据多体系统理论可有:
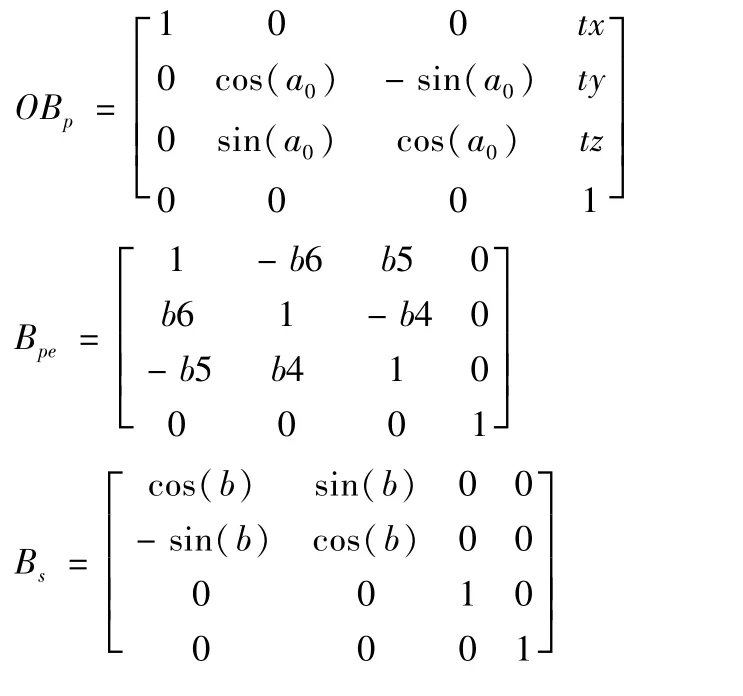
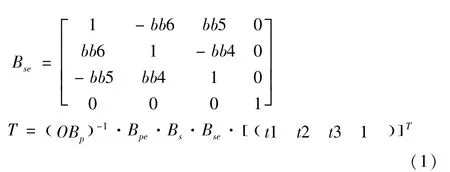
式中,a0=45°;(tx,ty,tz)T表示B轴理想坐标系在基坐标系O中的位置坐标;(t1,t2,t3)T表示球杆仪吸附在刀具端的小球在基坐标系中的位置坐;为研究方便,在B轴理想坐标系中研究球杆仪两端小球的坐标表达以及相对位置变化情况,在X向测量模式中,(t1,t2,t3)T=(0,0,H)T,tx=0。带入(1)后整理得到两球在B轴旋转了角度b后在其理想坐标系中的位置表达。
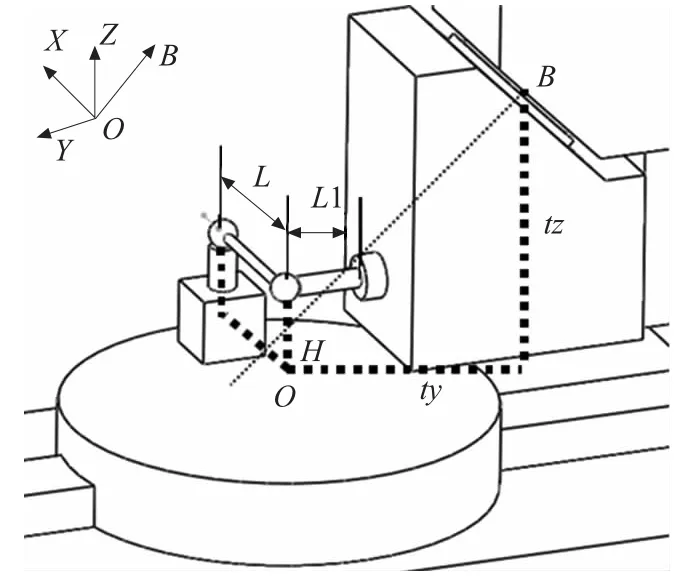
图2 X方向测量模式一
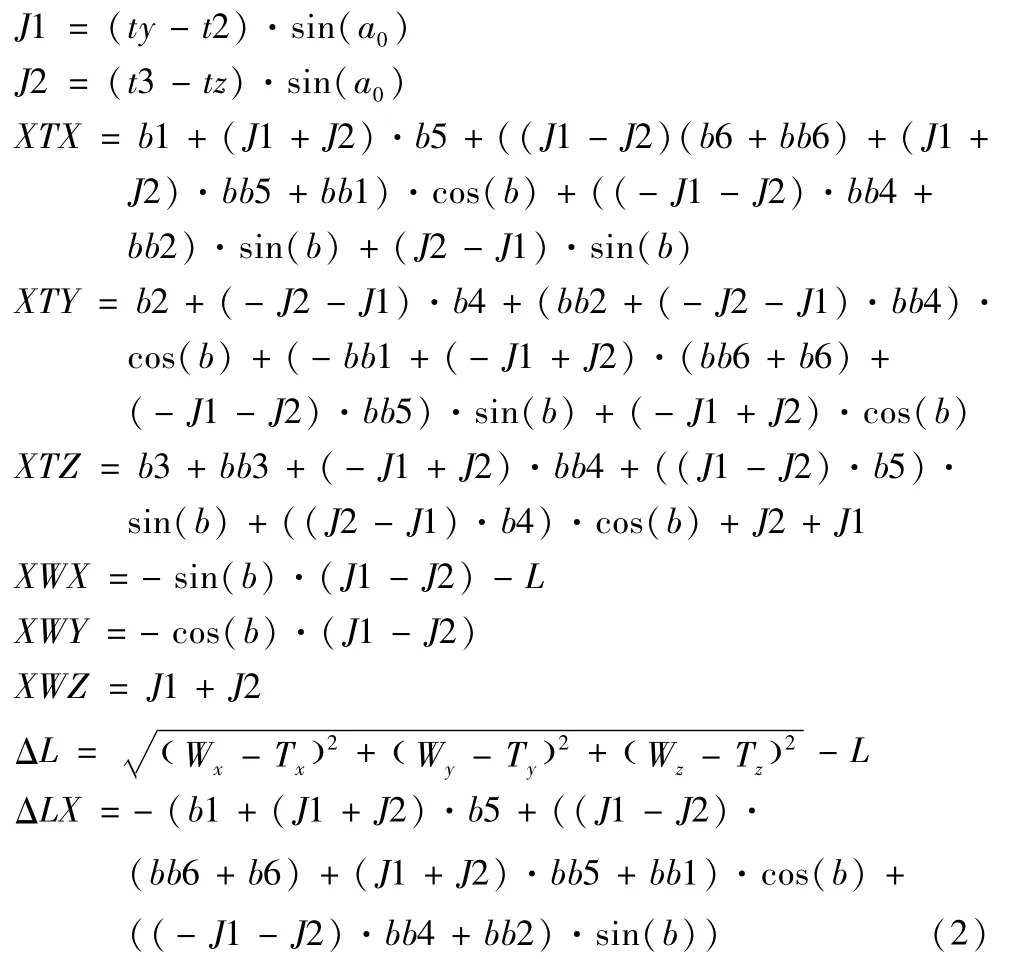
在初始位置,即b=0时,可以视作所有的动态误差值为0。观察发现,当分别在不同的ty和tz模式下测量时,即分别在不同的J1、J2模式下测量(分别进行X方向测量模式一、二)时,可有等式(3)。

根据等式(3)可以解出b5、b6,再结合等式(4)可以解出b1。
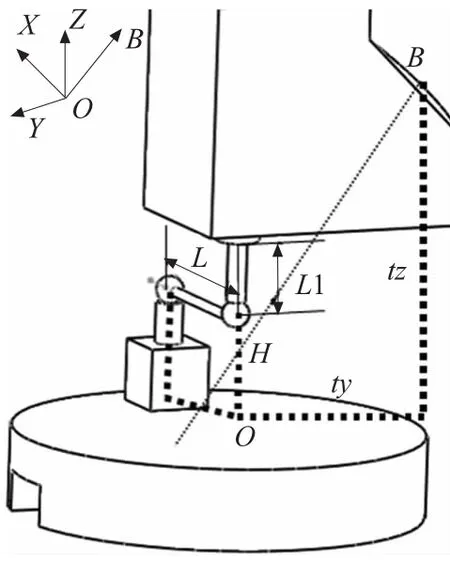
图3 X方向测量模式二
如图3所示,要实现X方向测量模式二,需要将B轴旋转180°后,布置球杆仪等测量装置进行实验测量。
按照图4布置Y向测量模式,在Y向测量模式中,(t1,t2,t3)T=(0,0,H)T,tx=0。同理根据多体系统理论,得到两球在B轴旋转了角度b后在其理想坐标系中的位置表达。

图4 Y方向测量模式
2.2 Y方向测量模式
如图4,进行Y向测量。在Y向测量模式中,(t1,t2,t3)T=(0,0,H)T,tx=0。同理根据多体系统理论,可解得在两球在B轴旋转了角度b后在其理想坐标系中的位置表达为:
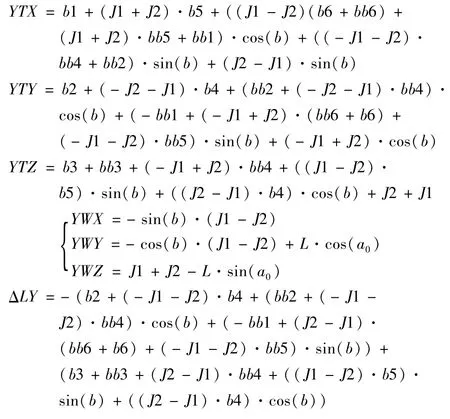
2.3 Z方向测量模式
如图5,进行Z向测量。在Z向测量模式中,(t1,t2,t3)T=(0,0,H+L)T,tx=0。同理在Z向测量模式中,根据多体系统理论,可解得两球在B轴旋转了角度b后在其理想坐标系中的位置表达。
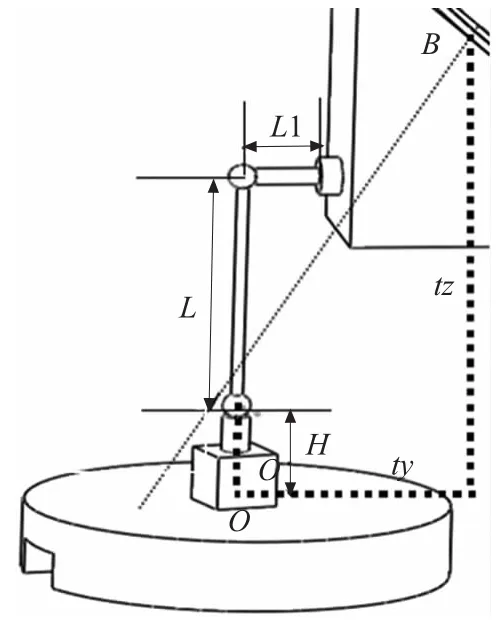
图5 Z轴方向测量模式

对于式子(3),当分别在不同的ty模式下测量时,可以分别解出b4,b2:

同理,结合分别在不同的ty和tz模式下测量结果,即分别在不同的J1,J2模式下测量(分别进行X方向测量模式一、二)时,即可解出bb2,bb4,bb5,bb6,bb1。考虑篇幅有限,不在此给出解答结果。最后结合等式(5)可解出bb3。

3 结论
本文在现今对于普通正交五轴数控机床旋转轴静态误差辨识研究比较成熟的基础上,基于多体系统理论建立分别安装在工件端和刀具端的球杆仪小球的运动误差模型,在对其运动表达式深入分析和归纳后,有针对性的设计8种测量方案,全面实现了对斜摆轴B轴存在的12项包含静态误差和动态误差的辨识,经实验验证,方案可行,测量效率较高,为非正交五轴数控机床旋转轴误差辨识提供了参考。
[1]李吉平.多轴数控加工相关数学模型的建立及应用[J].机械设计与制造,2000(2):43-44.
[2]M.Tsutsumi,A.Saito.Identification and compensation of systematic deviations particular to 5-axis machining centers[J].International Journal of Machine Tools and Manufacture,2003(43):771-780.
[3]Kwang-II Lee,Seung-Han Yang.Measurement and verification of position independent geometric deviations ofa five axis machine tool using a double ball-bar[J].International Journal of Machine Tools and Manufacture,2013(70):45-62.
[4]S.Ibaraki,W.Knapp.Indirect measurement of volumetric accuracy for three-axis and five axis machine tools:a review[J].International Journal of Automation Technology,2012(6):110-124.
[5]D.K.Lee,Z.K.Zhu,K.I.Lee,S.H.Yang.Identification and measurement of geometric deviations for a five-axis machine tool with a titling head using a double ball-bar[J].International Journal of Pecision Engineering and Manufacturing,2011(12):337-343.
[6]韩越梅.加工中心自动换刀装置的研究进展[J].装备制造技术,2010(5):128-129.
[7]M.Tsutsumi,A.Saito.Identification and compensation of systematic deviations particular to 5-axis machining centers[J].International Journal of Machine Tools and Manufacture,2003(43):771-780.
[8]Kwang-IILee,Seung-Han Yang.Measurement and verification of position independent geometric deviations of a five-axis machine tool using a double ball-bar[J].International Journal of Machine Tools and Manufacture,2013(70):45-62.
[9]S.Ibaraki,W.Knapp.Indirect measurement of volumetric accuracy for three-axis and five-axis machine tools:a review[J].International Journal of Automation Technology,2012(6):110-124.
(编辑 李秀敏)
Research on the Geometric Deviations Identification of Nonorthogonal Five Axis NC Machine Tool Rotation Axis
FAN Jin-wei,WANG Zhi-yuan,TANG Yu-hang
(College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology,Beijing 100124,China)
Considering the fact that there is not enough study on the identification of the geometric deviations generated by inclined pendulum shaft axis B of nonorthogonal five axis nc machine tool at home and abroad,establish nonorthogonal five axis nc machine tool motion deviations model based on the multi-body system theory which takes rotation axis B static deviations and dynamic deviations totaling 12 into consideration.After analyzing the mathematical expression of motion deviations model and combining Renishaw company QC10 instrument,eight different measurement model is designed.At last,combined with the measuredment results,the 12 geometric deviations of pendulum shaft axis B can be identified fast and efficiently.This method has been verified by experiments,which can be applied into the identification for nonorthogonal five axis nc machine tool.
non-orthogonal five-axis NC;inclined axis;multi-body system;geometric deviations;identification algorithm
TH132;TG659
A
1001-2265(2015)01-0071-04 DOI:10.13462/j.cnki.mmtamt.2015.01.020
2014-04-01
国家自然科学基金:数控机床加工缺陷成因的逆向追踪理论与实验研究(51275014);国家科技重大专项:中高档国产数控磨床可靠性规模化提升工程(2013ZX04013047)
范晋伟(1965—),男,河南西平人,北京工业大学教授,工学博士,研究方向为数字化精密加工与检测;通讯作者:王志远(1988—),男,山东龙口人,北京工业大学硕士研究生,研究方向为数控曲面加工缺陷逆向追踪,(E-mail)821866169@qq.com。
