数控机床主轴绿色配置设计的不确定优化模型建立与求解*
2015-11-03胡浩平刘电霆
胡浩平,刘电霆
(桂林理工大学a.信息科学与工程学院;b.机械与控制工程学院,广西桂林 541004)
数控机床主轴绿色配置设计的不确定优化模型建立与求解*
胡浩平a,刘电霆b
(桂林理工大学a.信息科学与工程学院;b.机械与控制工程学院,广西桂林 541004)
以MJ-50型数控车床主轴的模块化绿色配置设计为例,将技术性能最优、经济成本低、环境影响最小、能耗最少设为目标函数,建立包含模糊数与区间数的不确定组合优化模型;按三角模糊数和区间数的运算法则将其转换为确定型模型,并采用权重系数法把该多目标优化问题转化为单目标优化问题;采用离散二进制粒子群优化算法进行模型求解,获取最优解。实验证明该方法可行。
绿色配置;多目标优化;不确定优化;二进制离散粒子群算法
0 引言
绿色设计(Green Design)[1]为众多企业走出资源利用率低、能源消耗高、对环境影响大的困境创造了机遇。产品的绿色配置不但能给企业带来强有力的竞争力,更是大势所趋。目前一些研究[2-5]考虑了绿色就没有考虑不确定因素,考虑了优化就没有不确定变量集,考虑了多目标就没有考虑不确定性模型的求解;所以本文结合绿色因素、模糊数以及区间参数、多目标函数规划和粒子群优化算法,就基于模块化的数控机床配置设计进行不确定模型建立和确定模型转换,利用离散二进制粒子群算法求解,结果证明这是可行的。
1 不确定数学概述
1.1 三角模糊数的运算法则
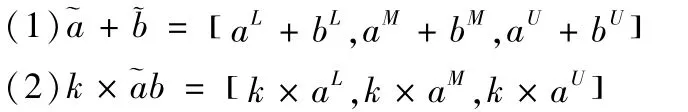
三角模糊数的确定方法有多种,这里采用加权重心法,即利用以下公式:
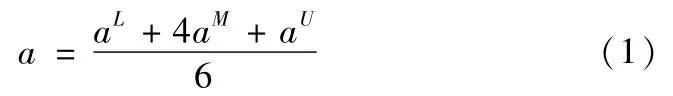
将三角模糊数转化为确定数a。
1.2 区间数的运算法则
类似于实数的二元运算:+,-,×,/,区间数也有自身的二元运算,对于区间数A=[aL,aR],B=[bL,bR],λ为实数,两区间数有下面几种运算[7]。
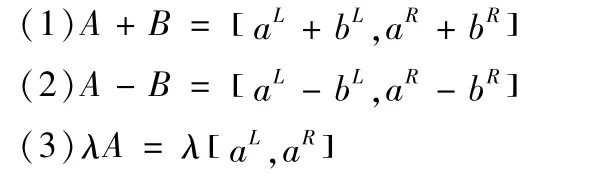
Min f( X,U)为带有区间数的目标函数,清晰化转化过程如下:
目标函数

引入权系数β∈[0,1],目标函数公式(2)可转化为如下单目标形式(5):
2.4 实例的不确定模型规划
在数据库中将会一个部件配有一个表,表结构形式如表1所示,以脉冲编码器表为例子,该表是部件脉冲编码器数据库表,记录数为5条,求其中最优的一条作为结果值,具体的求解权重参数设置如下:ω1=0.25,ω2=0.25,ω3=0.25,ω4=0.25,ω11=0.25/4,ω12=0.25/4,ω13=0.25/4,ω14= 0.25/4,ω21=0.25/4,ω22=0.25/4,ω23=0.25/4,ω24=0.25/4,ω31=0.3564·0.25/5,ω32=0.2296· 0.25/5,ω33=0.2296·0.25/5,ω34=0.2296·0.25/ 5,ω35=0.0922·0.25/5,ω41=0.25/3,ω42=0.25/3,ω43=0.25/3[10]。
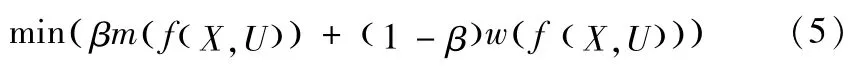
2 数控机床主轴绿色配置设计的不确定模型规划
2.1 模块规划
数控机床模块化一般是指使用模块的概念对产品或系统进行规划设计和生产组织,通过模块的选择和组合可以构成不同的产品,以满足市场不同需求的设计方法,实现最佳的效益和质量,本文是基于数控机床中关键部件主轴装置进行的绿色概念配置设计,设计出绿色最优的产品。以MJ-50型数控车床主轴箱[8]结构为例,如图1所示。
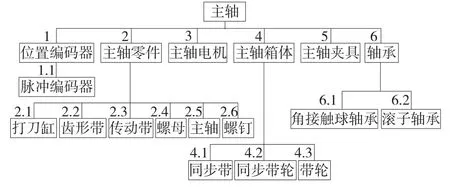
图1 主轴关键部件结构
绿色设计目标如图2[9]:
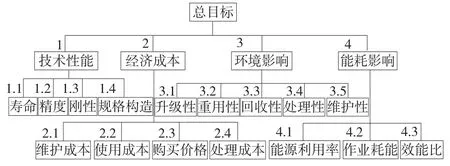
图2 绿色配置设计多目标
2.2 部件属性表构建
每个部件提供多种产品,相关指标属性大部分用“很好”、“好”、“较好”、“一般”和“无”5个语言标度度量,用三角模糊数[0.6,0.8,1]、[0.4,0.6,0.8]、[0.2,0.4,0.6]、[0.0,0.2,0.4]和[0.0,0.0,0.0]来表达,也有部分指标是用区间数来表示。
2.3 总多目标不确定模型规划
本主轴产品有14个部件组成,而且每个部件中的产品都是有且仅有一个被选中,设最后选出的14个部件是{X1,X2,X3,X4,X5,X6,X7,X8,X9,X10,X11,X12,X13,X14},所以总目标可以表述为:

某一部件多目标最优可表示为一四元组,T max为技术最优,C min为成本最优,E max环境影响最优,G max为能耗影响最优,假设各权重系数为:技术性能ω1,经济成本ω2,环境影响ω3,能耗影响 ω4,寿命ω11,精度 ω12,刚性 ω13,规格构造 ω14,维护成本ω21,使用成本ω22,购买价格ω23,处理成本ω24,升级性ω31,重用性ω32,回收性 ω33,处理性 ω34,维护性ω35,能源利用率ω41,作业耗能ω42,效能比ω43。采用加权系数法,将多目标转化为单目标求解:

总多目标数学模型为式(8):
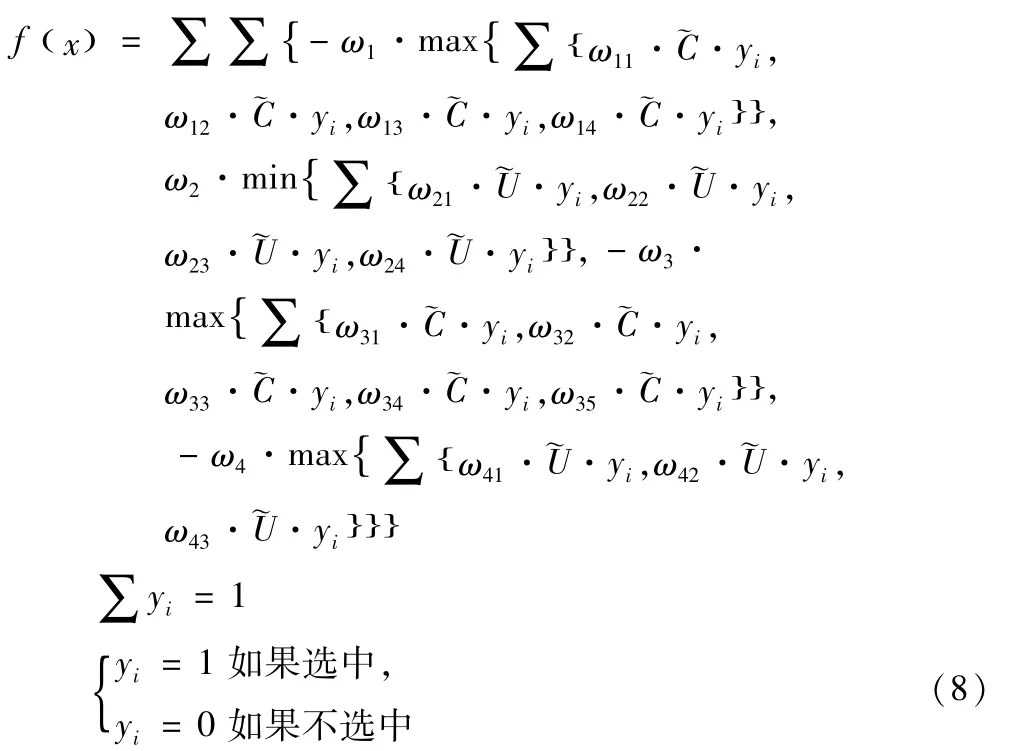

表1 脉冲编码器绿色属性
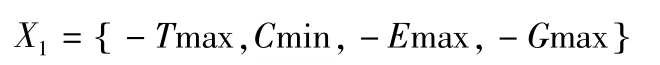
这是X1的多目标优化模型如式(9):

要考虑区间数和模糊数的取值要统一,不能出现区间数过大而导致模糊数忽略不计的情况,一般需要无量纲化。
3 二进制离散粒子群优化算法求解
3.1 二进制离散粒子群算法
1997年,Kennedy和Eberhart为解决工程中的组合优化问题[11-12],提出PSO算法的二进制BPSO离散版,该算法中每个粒子的位置向量用二进制数0和1表示,但是其速度向量仍然属于实数空间R,并且有v[i][j]∈[-v_max,v_max]。这样,算法基本粒子群算法中的速度公式仍然保留,而只修改其位置更新公式得到,Kennedy等提出利用Sigmoid函数在原来位置基础上来得到位置向量的值,Sigmoid函数是常用在神经网络中的一种非线性函数,经过改造每个粒子的速度和位置更新公式为式(10)、(11):

当rand()<1/(1+e-v[i][j]),p[i][j]=1;其他,

3.2 求解算法
本文的BPSO求解步骤如下:
①初始粒子群:将问题每一个解采用二进制编码表示;随机初始5个二进制位,产生10个粒子;比如10010,11111,00100等。
②计算每个粒子的适应值:每个粒子位串解码得到参数,由参数得到目标函数值;在编码中会有一些比如10010、11111等不合格的编码其适应值用一个极大常数表示,而比如01000等合格的编码其适应值为第二个记录的目标函数值。
③更新个体最优值及全群最优:与现有各粒子的适应值作比较更新个体最优和全局最优;
④产生新的粒子群编码:按式(12)计算每位的更新概率,产生新的粒子群;

⑥若迭代条件满足,再输出全局最优粒子的目标值。否则转入②。
采用C_FREE5.0为运行环境,C语言编写程序,粒子数目10,学习因子C1=2,学习因子C2=2,惯性权重0.5,最大迭代次数20次,获得的测试数据如表2。

表2 实验数据表
最后最优值:-0.076395;最后最优编码:00001;最好的记录是第5条;程序收敛很快,同时最后不管迭代多少次都收敛在一个固定的值了。
具体求解过程如图3所示。
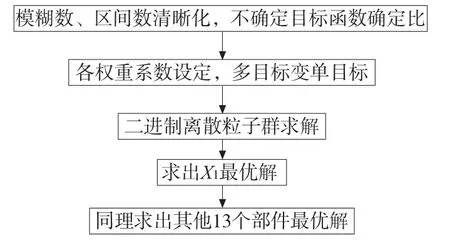
图3 求解流程
4 总结
对脉冲编码器表采用上述二进制离散粒子群优化算法,求得脉冲编码器最优解为:编码器A5;同样道理,得到其他13个部件最优值。本方法速度快,收敛稳定,可以减轻公司企业的劳动负担,具有很好的实用价值。本文采用传统的权重系数法求解有一定的弱点,系数设定反面人为影响因素较大;作者将继续深入研究,直接用离散的多目标粒子群进行求解不确定多目标数学模型将是下一步工作。
[1]刘光复,刘学平,刘志峰.绿色设计的体系结构及实施策略[J].中国机械工程,2000,11(9):965-968.
[2]谢立贰.数控机床模块组合研究[D].沈阳:东北大学,2010.
[3]王力.数控机床模块划分方法研究[D].沈阳:东北大学,2010.
[4]薄瑞峰,黄洪钟.蚁群算法在概念设计方案中求解的应用[J].西安交通大学学报,2005,11(39):1237-1240.
[5]许志力,史明华,肖放.基于模块化产品族的配置设计研究[J].设计与研究,2005,12(12):14-19.
[6]冉静学.三角模糊数排序方法的研究[J].中央民族大学学报(自然科学版),2011,20(4):37-42.
[7]王新端.基于区间数的不确定优化理论及求解方法研究[D].西安:长安大学,2012.
[8]蔡厚道,杨家兴.数控机床构造(第2版)[M].北京:北京理工大学出版社,2012.
[9]王春鹏.构建绿色设计的评价指标体系[J].包装工程,2009,30(12):12-14.
[10]唐涛,刘志峰,刘光复,等.绿色模块设计方法研究[J].机械工程学报,2003,39(11):149-154.
[11]陈自郁,何中市.一种求解集合组合问题的离散粒子群优化模型[J].华南理工大学学报(自然科学版)2010,38(4):141-146.
[12]李兰.改进的离散粒子群算法求解0_1背包问题[D].广州:华南理工大学,2011.
(编辑 李秀敏)
CNC Machine Tool Spindle Green Configuration Design Optimization under Uncertainty and Model Establishment
HU Hao-pinga,LIU Dian-tingb
(a.College of information science and engineering;b.College of Mechanical and Control Engineering,Guilin University of Technology,Guilin Guangxi541004,China)
Taking lathe spindle MJ-50 CNC modular green configuration design as theexample,Take technical performance of optimal,low economic cost,minimum environmental impact,energy consumption as objective function,establish uncertain portfolio optimization model whichIncludes the of fuzzy number and interval;according to the algorithm of triangular fuzzy number and interval number to convert it into a deterministic model,and using the weight coefficient method to the multi-objective optimization problem into a single objective optimization problem;using discrete particle swarm optimization algorithm to solve the model,and obtain the optimal solution.The experiment demonstrated the feasibility of this method.
green configuration;multiobjective optimization;uncertainoptimization;discrete particleswarm algorithm
TH122,TG65
A
1001-2265(2015)01-0038-04 DOI:10.13462/j.cnki.mmtamt.2015.01.011
2014-03-31;
2014-04-02
国家自然科学基金项目(51265008);广西自然科学基金项目(2012GXNSFAA053193);广西矿冶与环境科学实验中心重点项目(KH2011ZD003);广西汽车零部件与整车技术重点实验室项目(2013KFMS10)
胡浩平(1981—),男,湖南汨罗人,桂林理工大学讲师,硕士,研究方向为智能计算、制造业信息化,(E-mail)1628619275@qq.com。
