基于热—结构耦合的精密车床机械主轴热变形仿真的分析

史清华，张丽秀，吴玉厚，李金鹏

（沈阳建筑大学机械工程学院，辽宁 沈阳 110168）

基于热—结构耦合的精密车床机械主轴热变形仿真的分析

史清华，张丽秀，吴玉厚，李金鹏

（沈阳建筑大学机械工程学院，辽宁 沈阳 110168）

论文是以A2-6-200精密车床机械主轴为研究对象，通过使用SoildWorks建立主轴实体模型，简化后导入到有限元分析软件中，利用有限元法对其进行热分析，得到主轴温升和温度场分布情况，以求得温度场为依据进行热—结构耦合分析。通过在不同工况下的仿真结果分析，为预测机械主轴的热变形状态，提供了良好的参考依据。

机械主轴；温度场；热变形；热—结构耦合

0 引言

随着现代机械制造技术的发展，对机床的加工精度的要求越来越高，热变形导致机床误差问题也日益突出。研究实验表明，热误差是机床的最大误差源，占机床总误差的40%～70%［1］。主轴作为机床的重要组成部件，其性能的好坏直径影响机床整体水平。因此，主轴系统的热特性研究与分析对机床精度的保证至关重要。

日本的Moriwaki等通过实验研究了超精密机床的空气主轴系统的热特性，得出了热变形与主轴转速和环境温度之间的传递函数［2］。韩国的choijin Kyung等用有限元方法对主轴轴承系统进行了热特性研究［3］。上海理工大学建立了数控螺纹磨床主轴系统的有限元模型，分析了主轴系统的温度分布，通过“热-结构”耦合分析主轴系统瞬态热变形［4］。

本文是针对A2-6-200精密车床机械主轴，利用有限元法，建立“主轴—轴承”系统的仿真模型，并分别在粗、精加工两种不同方式的极限转速下进行“热-结构”耦合分析，从而能够有效地预测机械主轴的热变形情况。

1 机械主轴内部结构

主轴系统主要是由主轴、壳体、轴承端盖和前后圆柱滚子轴承及中间角接触球轴承等零件组成。车床进行粗加工时，主轴转速为0～1200r/min；精加工时，转速为1200～5000r/min。主轴右端是电机通过皮带带动轴上安装的皮带轮为其提供驱动力，左端与法兰盘相联接，从而夹紧工件进行车削加工。图1为精密车床机械主轴系统结构简图。

2 主轴的温度场计算

2.1热源分析

主轴系统热源主要有：电机发热、切削热、轴承摩擦发热。主轴是由电机通过皮带带动的，电机距离主轴较远，可以忽略电机发热对主轴系统的影响。切削热被冷却液和切屑带走，故主轴系统的主要热源是前中后轴承的摩擦热。

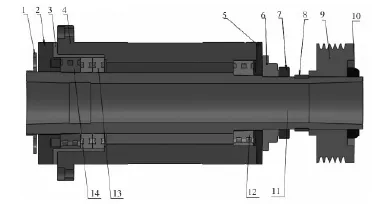
图1　主轴系统结构简图Fig.1 Structure diagram for spindle system

2.2发热量的计算

滚动轴承发热量主要是由轴承的摩擦力矩产生，其计算公式为［5］：

式中：Hf—轴承发热量（W）；n—轴承转速（r/min）；M—轴承摩擦力矩（N·mm）。轴承摩擦力矩的计算公式为：

式中：M0—与载荷无关的摩擦力矩（N·mm）；M1—与载荷有关的摩擦力矩（N·mm）。

（1）M0主要与轴承类型、润滑剂的黏度和数量、轴承转速有关，在高速轻载时，起主要作用。

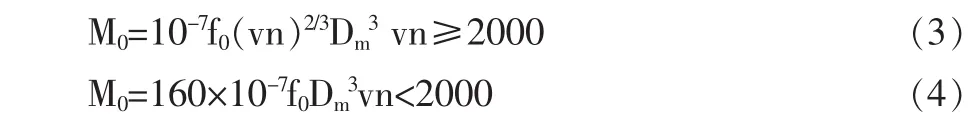
式中：v—在轴承工作温度下润滑剂的运动黏度（mm2/s）；n—轴承转速（r/min）；f0—与轴承类型和润滑方式有关的系数；Dm—轴承平均直径（mm），Dm=0.5（D+d）。

（2）M1是弹性滞后和接触表面差动滑动的摩擦损耗，低速重载时起主要作用。

式中：f1—与轴承类型和载荷有关的系数；P1—计算轴承摩擦力矩的轴承载荷（N）。

由公式（1）～（5），计算得到转速分别为500～5000r/min时各轴承的发热量，图2为各轴承在不同转速下的发热量情况。

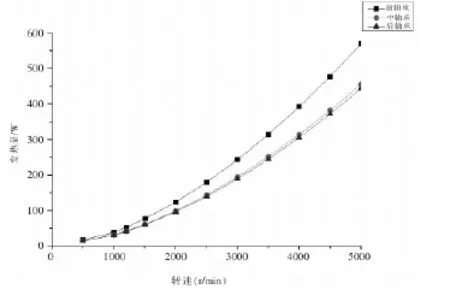
图2　各轴承发热量情况Fig.2 Each bearing calorific value

2.3换热系数的计算

此处主要是主轴旋转带动周围空气的流动形成的强迫对流换热。决定对流换热的换热系数的努谢尔特准则［6］：

式中：hc—对流换热系数（W/（m2·k））；λ—空气导热系数（W/（m·k）），环境温度为20℃时取2.67×10-2；Nμ—努谢尔特数；lc—特征尺寸（m）。强迫对流的努谢尔特计算公式为：

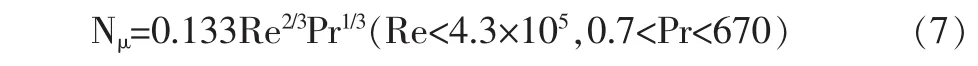
式中：Re—雷诺数；Pr—流体普朗多数，取0.707。由式（6）～（7）可得到在环境温度为20℃，转速为1200r/ min时，主轴内外表面对流换热系数分别为22.01W/（m2· k）、25.81W/（m2·k）；转速为5000r/min时，主轴内外表面对流换热系数分别为56.9W/（m2·k）、42.1W/（m2·k）。

3 主轴系统的热—结构耦合分析

使用SoildWorks建立实体模型，将其导入到有限元软件中进行温度场、热变形分析，定义材料为合金钢，环境温度为20℃。图3为不同主轴转速为条件的主轴温度。

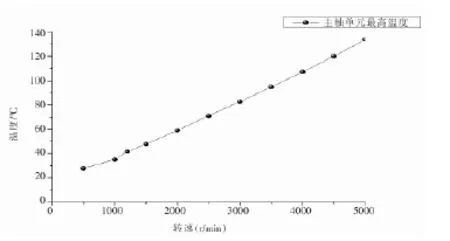
图3　不同转速条件下的主轴温度Fig.3 Spindle temperature under different speed condition

在车床进行粗、精加工条件下，此时分别以主轴的极限转速为1200r/min和5000r/min的情况为例，主轴的最高温度分别为41.562℃、133.9℃，都出现在中轴承内圈处，如图4所示。这主要是因为中轴承支撑的载荷比较大，发热也很大，而且轴承外圈的表面积比内圈大，内圈散热条件与外圈相比也比较恶劣。而主轴后端的温度相对较低，这有利于减少热变形，保证加工精度。

图4　主轴温度分布云图（转速为1200、5000r/min时）Fig.4 Spindle temperature distribution（Speed of 1200，5000r/min）

在主轴温度场的基础上，通过有限元分析中的热—结构耦合分析，可以求解其热变形。图5是转速为500～ 5000r/min时的主轴变形量及变化趋势，图6、7、8分别是主轴转速为1200r/min和5000r/min时主轴综合、轴向和径向位移变形云图。

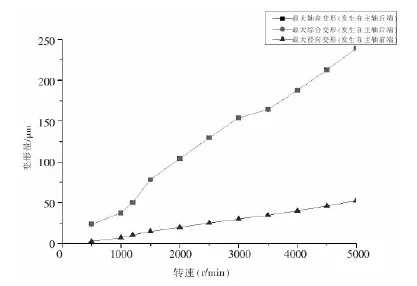
图5　不同主轴转速下的主轴变形Fig.5 The deformation of the spindle under different speed

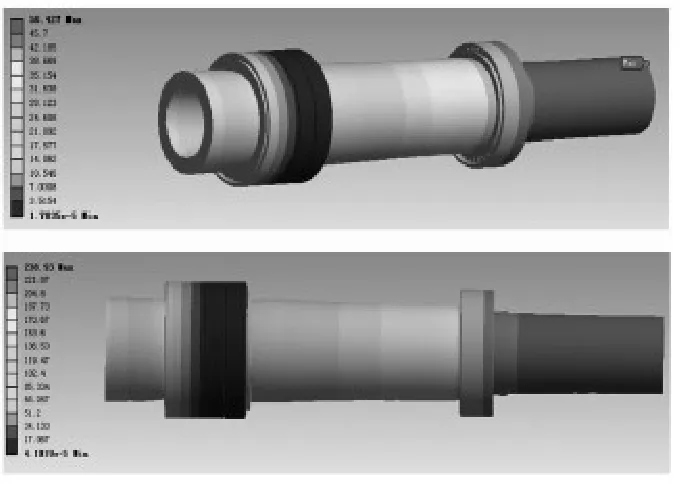
图6　主轴综合位移变形云图（转速为1200、5000r/min时）Fig.6 Deformation nephogram for spindle comprehensive displacement（Speed of 1200，5000r/min）

图7　主轴轴向位移变形云图（转速为1200、5000r/min时）Fig.7 Deformation nephogram for spindle axial displacement（Speed of 1200，5000r/min）

图8　主轴径向位移变形云图（转速为1200、5000r/min时）Fig.8 Deformation nephogram for spindle radial displacement（Speed of 1200，5000r/min）

由图5可以看出，随着主轴转速的增加，主轴前后端产生的各方向上的变形位移也随之增加。主轴的综合变形和主轴轴向变形明显后端比前端大，主轴径向变形也小于轴向变形，符合提高加工精度的要求。

4 结论

（1）通过有限元分析可知，主轴转速越高，轴承产生的发热量就越大，由此产生的温升变化对主轴热变形也越大，且与温度无关，这与实际情况相符。

（2）车床主轴在低速重载时进行粗加工时，随着转速升高，载荷要比转速对主轴热变形影响要大；而在高速轻载进行精加工时，转速对主轴热变形的影响要大得多。

（3）主轴热变形的最终结果是使前工作端抬头，主轴沿着轴向方向伸长，位移主要发生在主轴末端，它有利于加工精度的保证。而当主轴达到稳态时，主轴前端热变形是影响主轴精度的主要因素。

［1］D.A.Krulewich，Temperature integration model andmeasurement point selection for thermally induced machine tool errors，Mechantronics，1998，8.

［2］Moriwaki，Toshimichi，Shamoto.Analysis of thermal deformation of an ultraprecision air spindle system［J］.CIRP Annals-Manufacturing Technology，1998，47.

［3］Choi jin-Kyung，Lee Dai-Gil.Thermal-characteristics of the spindle bearing system with a gear located on the bearing span［J］.International Journal of Machine Tools and Manufacture，1998，38.

［4］应杏娟，李郝林.数控机床主轴系统热特性有限元分析［J］.工具技术，2010，1.

［5］秦大同.轴承（单行本）［M］.北京：化学工业出版社，2013.

［6］朱珍，等.主轴三维温度场及热变形分析［J］.工具技术，2008，4.

Thermal Deformation's Simulation Analysis of Precision Lathe Mechanical Spindle Based on the Thermal-structure Coupling

SHI Qing-Hua，ZHANG Li-Xiu，WU Yu-Hou，LI Jin-Peng
（School of Mechanical Engineering，Shenyang Jianzhu University，Shenyang Liaoning 110168，China）

The article was based on precision lathe mechanical spindle of the A2-6-200 as the research object.The three-dimensional physical model was builded and simplified on the using of SoildWorks.The thermal analysis and thermal-structure coupling analysis were conducted based on finite element method．The thermal analysis was conducted in the different kinds of condition.It can provide good reference predicting in the thermal deformation's state of the mechanical spindle．

mechanical spindle；temperature field；thermal deformation；thermal-structure coupling

TP391.9

A

10.3969/j.issn.1002-6673.2015.02.045

1002-6673（2015）02-120-03

2015-02-27

国家自然科学基金（51375317）；辽宁省科技创新重大专项（201301001）；教育部创新团队计划（IRK1160）

史清华（1989-），男，黑龙江黑河人，硕士研究生。研究方向：数控机床关键技术；张丽秀（1970－），女，辽宁沈阳人，教授，博士，硕士研究生导师。研究方向：电主轴单元关键技术及机电一体化。