齿轮图的孤立断裂度
2015-11-02张明瑜王世英
张明瑜,王世英
(1.山西大同大学数学与计算机科学学院,山西大同037009;2.山西大学数学科学学院,山西太原030006)
齿轮图的孤立断裂度
张明瑜1,王世英2
(1.山西大同大学数学与计算机科学学院,山西大同037009;2.山西大学数学科学学院,山西太原030006)
本文给出了齿轮图和它的补图的孤立断裂度。
可靠性;二部图;孤立断裂度
本文仅考虑简单图。设图G=(V(G),E(G)),其中V(G)和E(G)分别为图G的顶点集和边集。若|V(G)|=1,则称G为平凡图。设S⊂V(G),当G是完全图时,若G-S是平凡图,称S是G的一个点割。当G是非完全连通图时,若G-S是不连通的,则称S是G的一个点割。G的点割集:C(G)={S:S是G的一个点割}。二部图又称为偶图,如果图G的顶点集可以分为两个非空子集X和Y,使得每一条边都有一个端点在X中,另一个端点在Y中。设V'是V的一个非空子集,以V'为顶点集,以两端点均在V'中V的边的全体为边集所组成的子图称为G的由V'导出的子图,记为G[V']。G的孤立顶点数用i(G)表示。V(G)的一个子集S称为一个稳定集,若S中任意两个顶点在G中都不相邻。G的最大稳定集的顶点数称为G的稳定数,记为α(G)。其它未给出的定义见文献[1]。
轮图Wn是由一个n-圈和一个孤立点u组成,并且圈上所有点都和此孤立点相邻,圈上的点和此孤立点之间的边称为轮辐。设Wn是轮图且V(Wn)={v1,v2,…,vn,u} ,其中u是中心点,若Wn的n-圈上的每条边被剖分,则得到的新图称为齿轮图,记为Gn,每条边剖分时新加入的点构成的集合记为{u1,u2,…,un} ,显然v(Gn)=2n+1,ε(Gn)=3n。
定义1[2]设G是一个连通图。图G的孤立断裂度
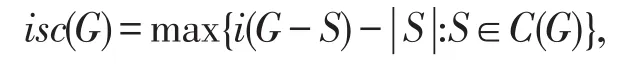
设S*是G的一个点割,若i(G-S*)-|S*|=isc(G),则称S*为一个孤立断裂度集。
引理1[2]若G是一个阶为n的连通图,则
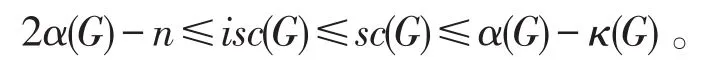
引理2[2]设G是一个连通二部图,那么isc(G)≥0。
定理1设Gn是一个齿轮图,那么isc(Gn)=1。
证明因为v(G)=2n+1,α(Gn)=n+1,则由引理1,有
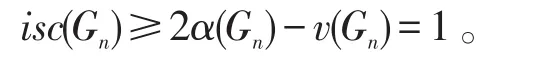
另一方面,设S是Gn的一个使|S|为最大的孤立断裂度集,V1是Gn-S的孤立点集。假设。那么令G1是Gn-S-V1的一个分支,S1是G1的一个孤立断裂度集,由于齿轮图是一个二部图,而二部图的任意导出子图也是二部图,所以G1是一个二部图。此外,由引理1,isc(G1)≥0。令。由于,所以有
Gn-S*不连通。因此
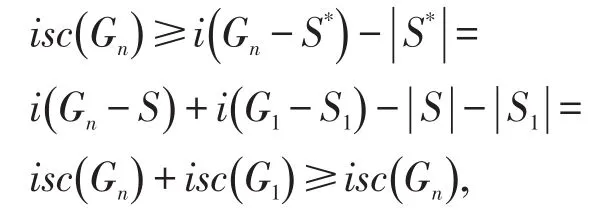
上式取等式,故S*也是一个孤立断裂度集且满足,与S的最大性矛盾。从而,进而。因为,
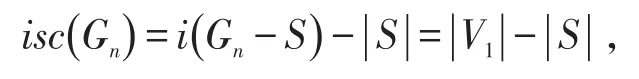
所以,
定理2设n是齿轮图Gn的补图,那么
证明因为齿轮图Gn是一个二部图,所以图n有两个完全图作为它的子图,记为Kn1,Kn2。
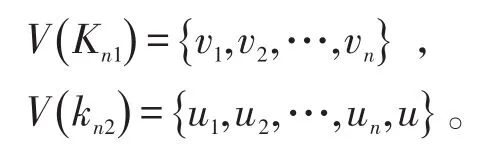
其中u和Kn1中的每个点都不相邻,u1,u2,…,un中的每个点都和Kn1中的n-2个点相邻。设S是的一个点割,则|S|≥n。否则,设|S|≤n-1。如果|S|=n-1时,S不是点割,那么|S|≤n-2时,S也不是点割。因此,设。再设则
情况1u∈S。
情况2u∉S。
在这种情况下,在u1,u2,…,un中,存在i+1个点不在S中。如果i≥2,在情况1中已经讨论过,-S连 通 ,所 以 设i=1 。 这 时|。当≥3时,由于V(Kn2)中的点u1,u2,…,un每个点都和v1,v2,…,vn中的n-2个点相邻,所以存在中的点在n-S中是相邻到中的点,n-S仍然连通。因此下面讨论i=1和n=3。在图1中,容易验证-S连通。
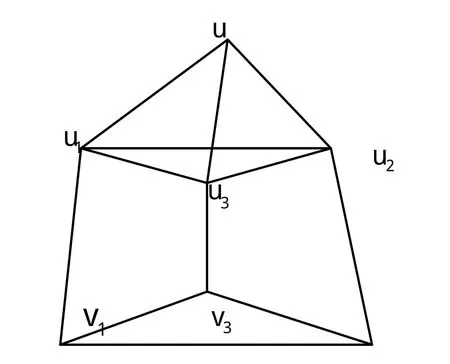
图1 ˉ3
因为Kn1,Kn2是的子图且,所以设有。再设且,则有设。因为Kn1,Kn2是的子图,,所 以。 取S=则S是点割且,因此
[1]Bondy J A,Murty U S R.Graph Theory[M].New York:Springer,2007.
[2]王世英,杨玉星,林上为,等.图的孤立断裂度[J].数学学报,2011,54(5):861-874.
〔责任编辑 高海〕
The Isolated Scattering Number of the Graph with Shape of the Gear
ZHANG Ming-yu1,WANG Shi-ying2
(1.School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009;2.School of Mathematical Sciences,Shanxi University,Taiyuan Shanxi,030006)
In this paper,we present the isolated scattering number of the graph with shape of the gear and its complement graph.
vulnerability;bipartite graph;isolated scattering number
O157.5
A
1674-0874(2015)03-0009-02
2015-03-24
张明瑜(1983-),女,山西应县人,硕士,讲师,研究方向:图论及其应用。
