一阶脉冲微分方程组周期边值问题正解的存在性

郭彦平，韩迎迎，李春景

（河北科技大学理学院，河北石家庄050018）

一阶脉冲微分方程组周期边值问题正解的存在性

郭彦平，韩迎迎，李春景

（河北科技大学理学院，河北石家庄050018）

研究一类一阶脉冲微分方程组周期边值问题正解的存在性问题。首先定义合适的线性空间以及范数,再给出恰当的算子,在非线性项和脉冲值满足一定的条件下，利用Krasnoselskii不动点定理,得到上述问题具有一个正解的充分条件。

Krasnoselskii不动点定理；正解；脉冲；微分方程组；周期边值问题

近年来，由于脉冲微分方程具有广泛的应用背景，已经成为一个重要的研究课题。

文献[1-2]对脉冲微分方程理论作了系统的研究和论述，建立脉冲微分方程的基本理论、周期解理论、线性系统、扰动系统、稳定性理论、解的渐进理论等。

由于脉冲微分方程自身特点，使其与一般常微分方程有明显不同。同时，一个简单的脉冲微分方程也会出现许多新的现象，例如，有规律的撞击现象、解的合并、解的不连续性等。有许多文献对其进行了研究[3-15]。

文献[16]研究了非线性一阶脉冲微分方程周期边值问题：

正解的存在性。

受上述文献的启发，研究如下非线性一阶脉冲微分方程组周期边值问题：

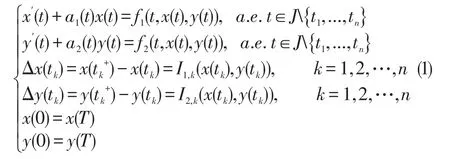
正解的存在性。

其中

1 预备知识

定义如下Banach空间：

定理1[16](Krasnoselskii不动点定理)设E是Ban⁃ach空间，P∈E是E的一个锥，Ω1,Ω2⊂E是开集，且若是全连续算子，满足下面两个条件之一：

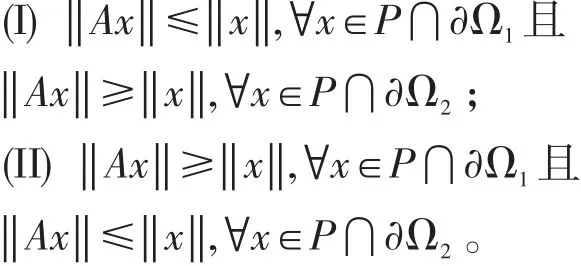
则A在上存在一个不动点。

定义1设E是Banach空间，P是E上的一个锥，称α是E上的非负连续凹泛函，如果是连续的，且对所有满足

定义2设0＜a＜b和r＞0，α是P上的非负连续凹泛函，定义凸集Pr和P(α,a,b)为

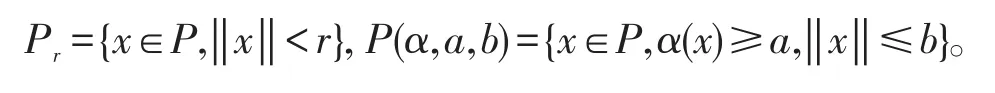
引理1[16]假设，满足，其中

则

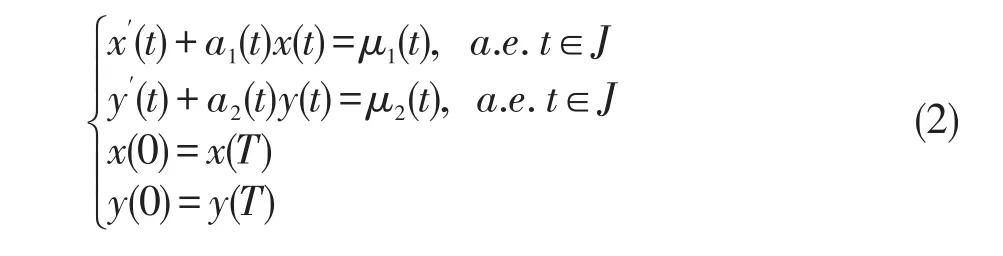
有唯一解为(x(t),y(t)),即

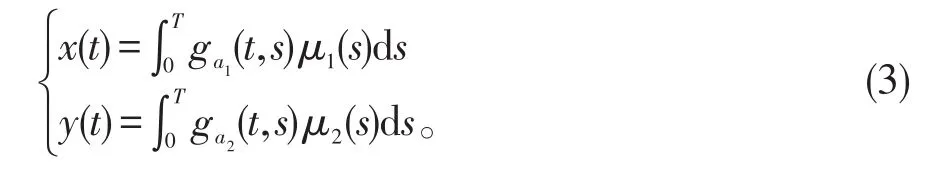
其中

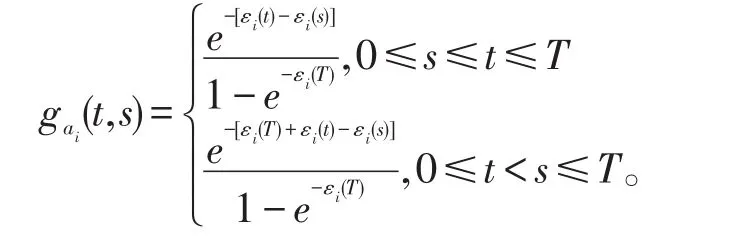
εi(T)≠0， 其中

则

引理2[16]假设满足

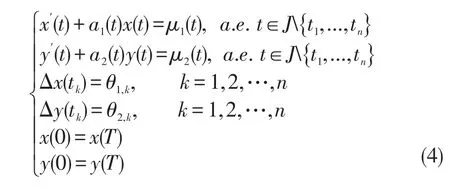
有唯一解为(x(t)，y(t)),即

引理3[16]设和满足，且

则线性脉冲微分方程组（4）的唯一解满足

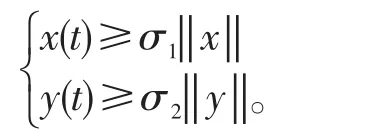
2 主要结果

定义X2=X×X,其中范数为

易知X2是Banach空间。

假设εi(T)≠0，i=1,2。根据引理2，(x,y)∈X2是非线性一阶脉冲微分方程组周期边值问题(1)的解的充分必要条件为

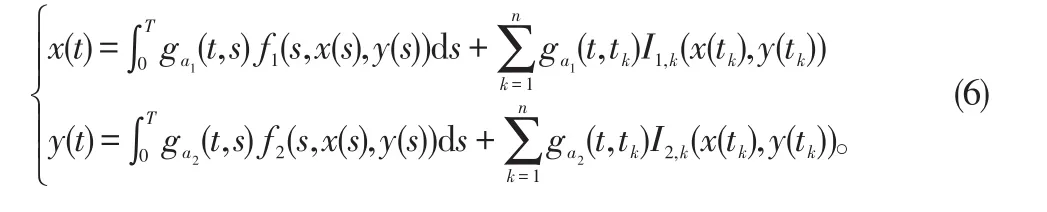
定义 算子

其中

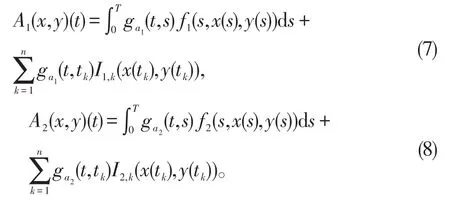
则算子A的不动点就是方程组(1)的解。

定义3称f(t,u,v)是脉冲Caratheodory函数,如果满足：

假设下面条件成立：

(A1)：fi,i=1,2.是脉冲Caratheodory函数，且

(A2)：Ii,k(k=1,2,...n,i=1,2)是 连 续 的 ，且 对)有

令

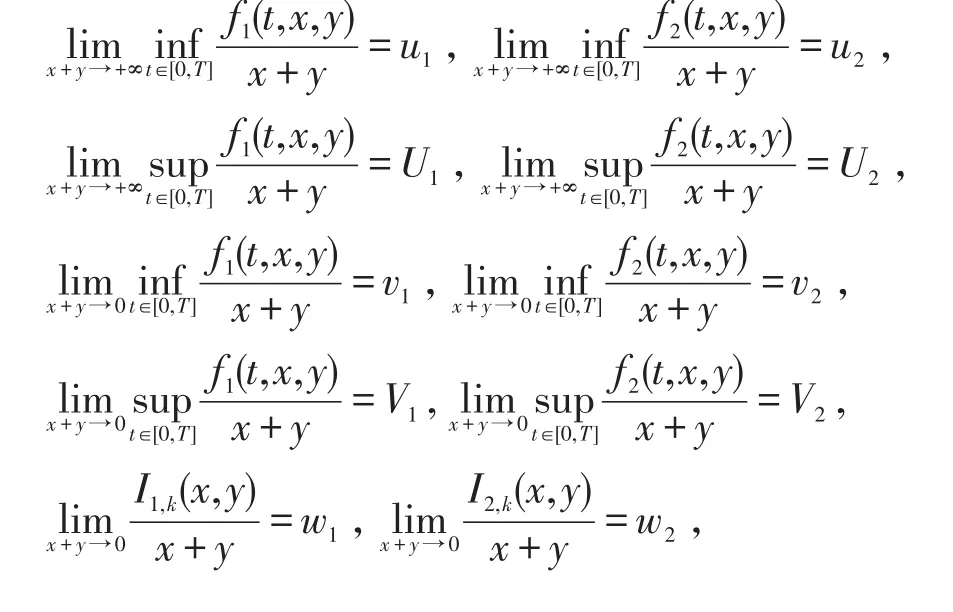
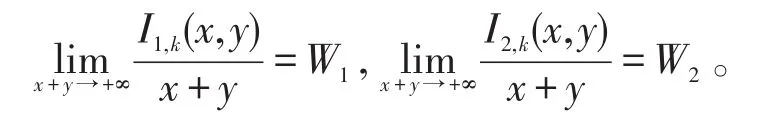
定理2假设 (A1)，(A2)成立，εi(T)＞0,i=1,2。U1,U2,v1,v2,w1,w2,W1,W2如上面所定义，并且满足：

和

则非线性一阶脉冲微分方程组周期边值问题(1)至少存在一个正解。

证明定义X2上的锥P:

易得(I)：

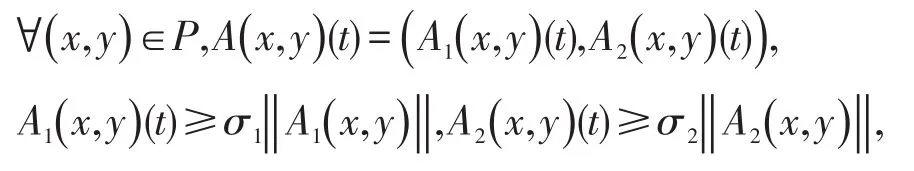
所以AP⊂P；

(II)：A是全连续的。

令η＞0满足，

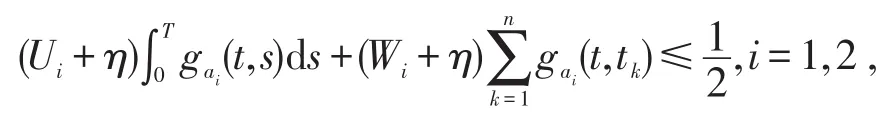
和

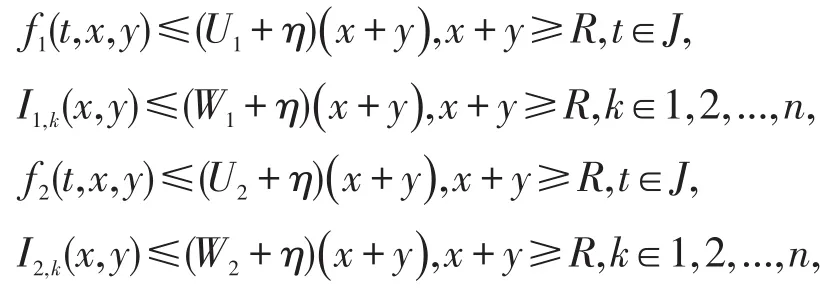
所以

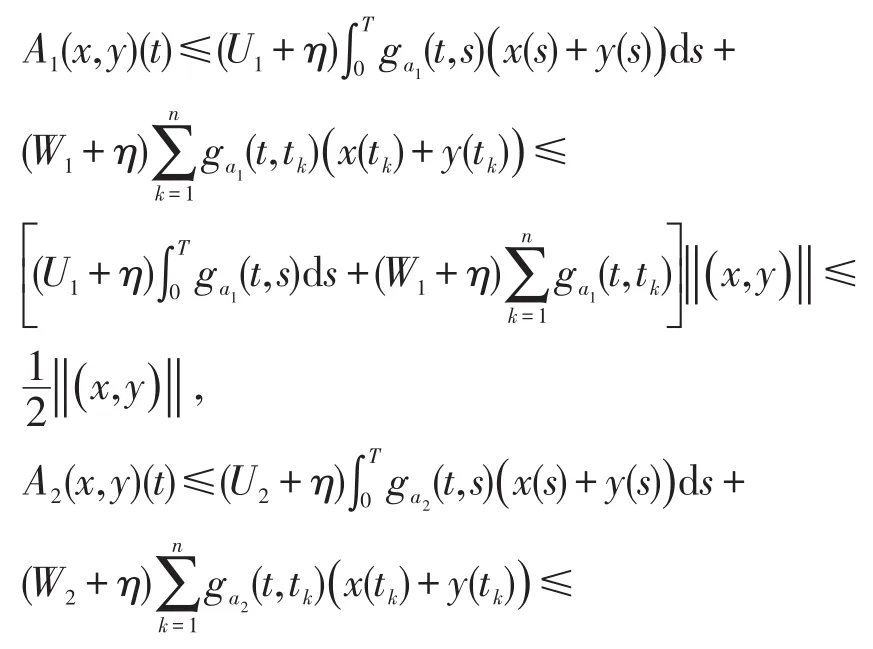
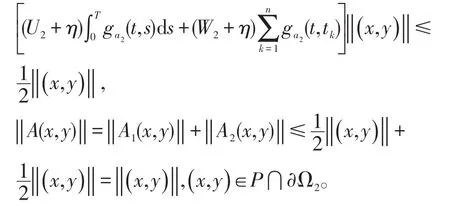
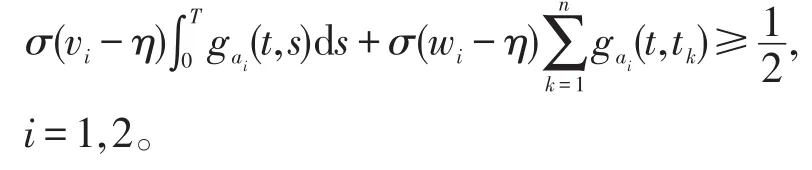
和

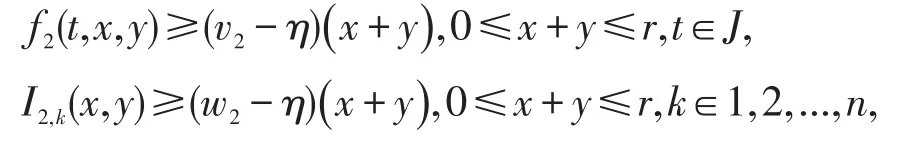
所以

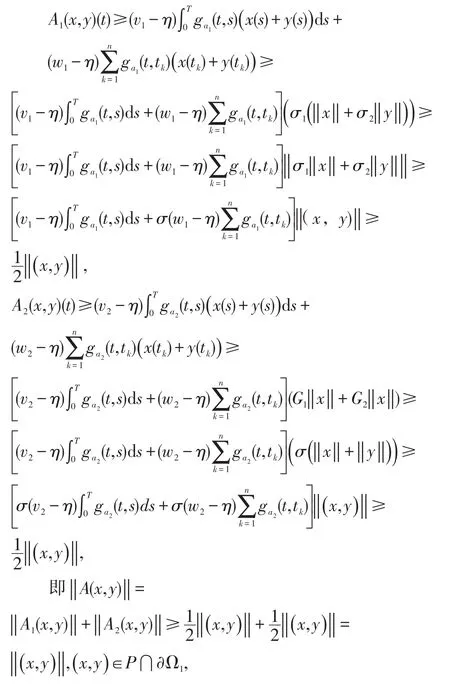
则利用定理1得A在上存在至少一个不动点，即是非线性一阶脉冲微分方程组周期边值问题(1)的一个正解。

推论1由定理2得当Wi=Ui=0，vi=wi=+∞,i=1,2时，非线性一阶脉冲微分方程组周期边值问题(1)至少存在一个正解。

定理3假设 (A1)，(A2)成立，εi(T)＞0,i=1,2。u1,u2,V1,V2,w1,w2,W1,W2如上面所定义，并且满足：

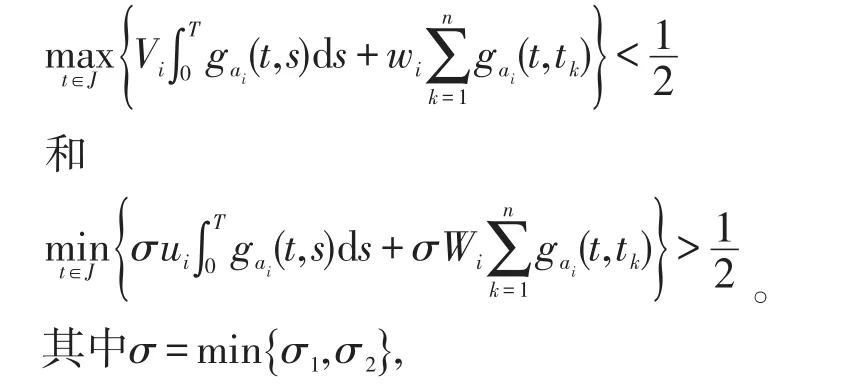
则非线性一阶脉冲微分方程组周期边值问题(1)至少存在一个正解。

类似定理2的证明，可得结论。

推论2由定理3得当ui=Wi=+∞,wi=Vi=0,i=1,2时，非线性一阶脉冲微分方程组周期边值问题(1)至少存在一个正解。

推论3如果存在和M,N,m,n满足

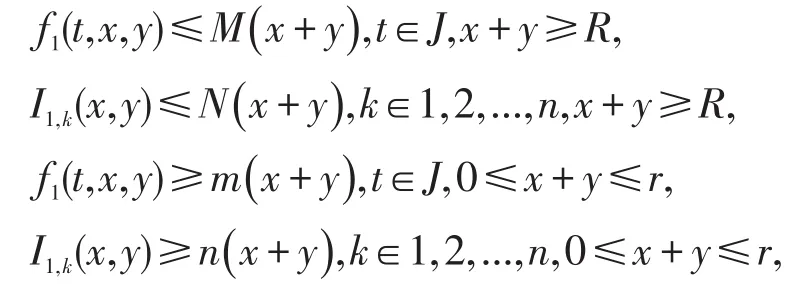
则非线性一阶脉冲微分方程组周期边值问题(1)至少存在一个正解。

推论4如果存在和M,N,m,n满足

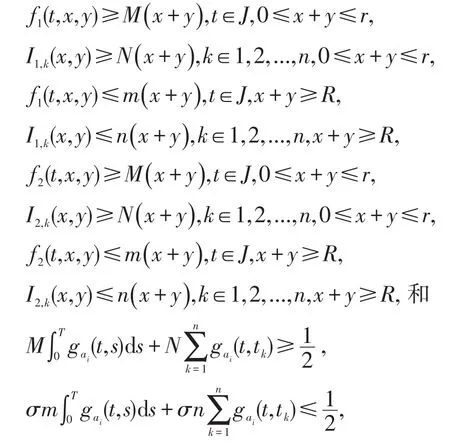
则非线性一阶脉冲微分方程组周期边值问题(1)至少存在一个正解。

[1]Lakshmikansam V,Bainov D D,Simeonoy P S.Theory of Impulsive differential equations[M].World Scientific:Singapore,1989.

[2]BAINOV D D,Simeonov P S.Impulsive differential equation:Periodic solutions and applications[M].Longman:Harlow,1993.

[3]Luo Z g,Shen J h,Nieto J J.Antiperiodic boundary value problem for first-order impulsive ordinary differential equations[J].Com⁃puter and Mathematics with Applications,2005,49(2):253-261.

[4]Chen L j,Sun J t.Nonlinear boundary Value problem of first-order impulsive functional differential equation[J].Journal of Mathe⁃matical Analysis and Applications,2006,318(2):726-741.

[5]李建利,申建华.一类脉冲泛函微分方程正周期解的存在性.应用数学,2004,17(3):456-463.

[6]Nieto J J.Periodic boundary value problems for first order impulsive ordinary differential equations[J].Nonlinear Appl,2002:51.

[7]Liu Y.Further results on periodic boundary value problems for nonlinear first order impulsive functional differential equations[J].J Math,Anal Appl,2007,327:435-452.

[8]Li X,Lin X,Jiang D,etal.Existence and multiplicity of positive periodic solutions to functional differential equations with impulse effects[J].Nonlinear Anal,2005,62:683-701.

[9]Liu Y,Ge W.Stability theorems and existence results for periodic solutions of nonlinear impulsive delay differential equations with variable coefficients[J],Nonlinear Anal.2004,57:363-399.

[10]He Z,Yu J.Periodic boundary value problems for first order impulsive ordinary differential equations[J].J Math Anal Appl,2002，272:67-78.

[11]Jiang D,Nieto J J,Zuo W.On monotone method for first order and second order periodic boundary value problems and periodic so⁃lutions of functional differential equations[J].J Math Anal Appl,2004，289:691-699.

[12]Hakl R,Lomtatidze A,Puza B.On a boundary value problem for first order scalar functional differential equations,Nonlinear Appl.2003，53:391-405.

[13]Li J,Nieto J J,Shen J.Impulsive periodic boundary value problems of first-order differential equations[J].J Math Anal Appl,2007，325:226-236.

[14]Jankowski T,Nieto J J.Boundary value problems for first order impulsive ordinary differential equations with delay arguments[J].Indian J Pure Appl Math,2007，38:203-211.

[15]Nieto J J,Rodriguez-Lopez R.Periodic boundary value problem for non-Lipschitzian impulsive functional differential equations[J].J Math Anal Appl,2006，318:593-610.

[16]Liu Yuji.Positive solutions of periodic boundary value problems for nonlinear first-order impulsive differential equations[J].Non⁃linear Analysis,2009，70:2106-2122.

〔责任编辑 高海〕

The Existence of Positive Solutions for Periodic Boundary Value Problems of First-order Impulsive Differential Equation Systems

GUO Yan-ping，HAN Ying-ying，LI Chun-jing
(College of Science,Hebei University of Science and Technology,Shijiazhuang Hebei,050018)

We study the existence of positive solutions for periodic boundary value problems of first-order impulsive differential equation systems.Firstly,appropriate linear space and norm are defined,and appropriate operator is given.Under the certain condi⁃tions of nonlinear term and pulse value,by the Krasnoselskii fixed point theory,we provide sufficient conditions under which the above boundary problem system has at least one positive solution.

Krasnoselskii fixed point theorem;positive solution;impulsive;differential equation;periodic boundary value prob⁃lem

O175.8

A

1674-0874(2015)03-0001-04

2015-03-24

国家自然科学基金资助项目[111371120]；河北省自然科学基金项目[A2013208147]

郭彦平（1965-），男，河北人，博士，教授，研究方向:微分方程边值问题。