高中数学解题思路多元化探析
2015-11-02江雪怡
江雪怡
(武汉外国语学校高一2班 湖北武汉 430022)
高中数学解题思路多元化探析
江雪怡
(武汉外国语学校高一2班 湖北武汉 430022)
数学是高中学习中的重点科目之一。受应试教育的影响,目前国内高中生学习数学时普遍采用题海战术,但这种方法容易造成学生解题思路被禁锢、思维能力和创造能力受到限制。一旦遇到新的题型,学生无从下手。探索高中数学的多元化解题思路,形成一题多解的思维模式,对于培养学生的发散性思维、逆向思维和创新思维帮助非常大。本文通过几个高中数学解题思路多元化的实例对上述观点进行了论证。
高中 数学 多元化
数学是高中学习的重点和难点科目。在解决数学问题的过程中,主要是对题目中的数量结构和数量关系进行学习和探索,找到最佳的解题方法和最佳的解题思路。一般的情况下,高中生会通过做大量的习题来寻找探索解题的方法。但是,这样容易造成解题思路被固定到一个模式,从而导致学生对题目给出的信息难以快速分析和反应,解题思路受到限制。同时,目前高中数学教材中的例题,普遍只提供一种解题思路或一种解决方法。学生长期局限于单一的解题方法,思维模式易被禁锢。在遇到新问题时,不容易从多个角度思考探索,在一定程度上限制了学生的思维模式,不利于学生对于问题的发散性思考和知识网络的建立。因此,我们高中生在数学学习中,应当注重探索一题多解,形成多元化的解题思路,这对于提高我们的逻辑思维能力,培养发散性思维、逆向思维和创新思维非常重要。[1]
思维能力提升了,我们的解题能力就会有质的飞跃。下面,本人就通过几个实例对高中数学解题多元化思路进行一些粗浅的探索。
一、一题多解培养高中生发散思维
数学科目对于我们学生来说是比较抽象的学科,在学习数学的过程中我们通常都是通过做大量的习题来寻找和熟悉解题思路。但是通常学习和找到的都是一种解题思路,经过大量的练习之后就熟悉了这种解题思路,导致在遇到类似的问题,只会用这一种思路解决问题,我们的思维被固定化了,没有过多的思考空间,在遇到与之不相同的问题时,就不能快速的找到其他的解题方法。个人认为,与做大量的习题比起来,培养锻炼我们的发散性思维是比较重要的。这样,我们也可以掌握多种解题思路和方法,可以应对多种题型,真正提升数学解题能力。[2]
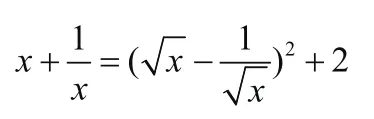

所以f(x)的值域是[2,)+∞。
上面的举例,一个题目、两种方法,给学生多提供了一种解题思路。探索“一题多解”,可以帮助我们从多个角度考虑问题,提高发散性思维和解题能力。
二、一题多解培养高中生逆向思维
思维过程的方向性也可以分为逆向思维和传统思维方式,也就是正向思维,它们是相辅相成的两种思维方式。但是,目前我们所学习的教材上很少涉到逆向思维,一般情况在数学学习过程中大部分我们只会用正向思维思考问题,限制了我们思维的发展。在数学学习中,实际遇到的一些问题用正向思维思考也比较麻烦,这就需要我们找寻和学习另外的思维方式。[3]
例题2:已知a2+b2=1,x2+y2=1,求证

因为a2+b2=1,x2+y2=1
即(a-x)2+(b-y)2≥0
由于最后等式不成立,且步步可逆,所以原不等式成立。解法三:用反证法
因为,a2+b2=1,x2+y2=1
显然上式不成立。
解法一采用的是正向思维解题,但第一步和第二步这两个步骤难想得到;解法二和解法三都是采用逆向思维解题,在思维上却较顺理成章,较容易想到。因此,在高中数学解题过程中,如果采用三、一题多解培养高中生创新思维
传统方法有困难时,可尝试采用逆推法和反证法。
“一题多解”可以改变解决问题的方法和形式,对于提升我们的创造性很有帮助。如我们在解不等式2<|2x-1|<6时,可以采用多种解题方法。
解法二:变换不等式,去除绝对值,即2<2x-1<6或-6<2x -1<-2,从而得出结果{x|-5<x<-1/2,或2/3<x<7/2}。
从上述例题可以看出,高中数学解题思路多元化,可以帮助我们找到多种解题途径和方法,帮助我们从各种不同角度思考问题,提高我们的思维活跃程度,让我们主动的对题目进行研究和探索,从而培养我们的创新力。
结语
数学是高中学习中的重中之重。在学习过程中,我们高中生不能沉湎于题海模式,要注重探索“一题多解”的解题方法,形成多元化的解题思路,以培养自己的发散性思维、逆向思维和创新思维,全面提升数学解题能力。
[1]许诺.关于高中数学函数解题思路多元化的方法举例探索[J].科学大众(科学教育),2016,(2):25.
[2]丁聪.高中数学多元化策略变革分析--以函数内容为例[J].数学教学通讯,2016,(12):46-47.
[3]旷昕宇.关于高中数学函数解题思路多元化的方法举例探讨[J].科学大众(科学教育),2016,(3):27.
