连续变量量子保密通信技术

王怀胜， 杨杰

(中国电子科技集团公司第三十研究所，四川成都610041)

0 引言

现代社会对信息资源、信息技术、信息产业的依赖程度越来越大，信息安全问题日益突出。信息安全问题是关系国防安全的战略问题，关系着国家和民族的根本利益，单纯依靠现有经典技术很难从根本上解决这一难题。量子保密通信，即量子密钥分发(Quantum Key Distribution，QKD)，是目前科学界公认的无条件安全(unconditional secure)保密通信方式，具有极高的军用和民用意义，是当前国际高科技竞争的前沿热点问题。

QKD技术主要分为离散变量(即单光子)和连续变量两大技术途径。经过近三十年的发展，单光子QKD技术发展已经较为成熟，却依然存在如下局限性。第一，单光子量子信号产生困难。实际系统中一般采用微弱激光脉冲来代替单光子，该方法效率较低，而且有一定几率产生多光子，产生潜在的安全漏洞，必须结合诱骗协议才能抵御光子数分离攻击。第二，通信波段单光子检测成本高、速率低、效率低，技术相对不成熟，未达到商用水平。第三，成本高昂。与单光子技术相比，连续变量技术一般以高斯态变量作为信号载波，利用光场的振幅和相位分量作为信号载体，采用平衡零差探测技术对经强度和相位调制后的光信号进行检测从而获得信息，无需单光子源和单光子探测器，大部分器件与经典相干光通信通用，具有高重复频率和高密钥速率的发展潜能，在成本和性能方面具有突出优势，发展前景光明。2013年之前，连续变量量子保密通信的无条件安全性证明和数据后处理存在较大难度，其受重视程度和发展成熟度远不如单光子技术。

2013年以来，连续变量量子保密通信(CVQKD)在理论研究和实验技术上有了巨大的飞跃:利用相空间上的旋转不变性，连续变量相干态CVQKD协议的无条件安全性首次被严格证明;高性能连续变量纠错码方案被提出并实时实验实现。上述两项工作为CVQKD的实际应用扫清了障碍。2013年，法国高等光学所法布里实验室的研究人员实现了80km传输距离的光纤CVQKD系统，将之前的最远传输距离世界纪录提升三倍，大大提升了CVQKD技术的实用性。CVQKD技术是未来量子保密通信技术的重要发展方向，虽然当前的CVQKD技术相关成果仍然主要停留在实验室阶段，但在关键基础理论和实验技术已基本解决的情况下，相信CVQKD技术将在不远的将来迎来快速发展，实用化进程得到极大促进。推进CVQKD技术的实用化与产品化、关注CVQKD的实际安全性正当其时。

本文将综述CVQKD的技术发展历史和现状，分析技术发展趋势，探讨未来重点突破方向，提出发展建议。

1 连续变量量子保密通信技术的发展里现状

1.1 澳大利亚

CVQKD技术研究起源于澳大利亚。1999年，澳大利亚国立大学的T.Ralph首次提出CVQKD协议，并简要分析了其安全性［1，2］。随后，昆士兰大学的M.Reid提出了一个基于连续连续变量纠缠态的离散调制CVQKD协议［3］。2004年，澳大利亚国立大学的C.Weedbrook提出了基于高斯调制相干态和外差检测的无开关协议(no－switching protocol)［4］，该协议可在保证无条件安全性的前提下提高安全密钥产生速率，是主流CVQKD协议之一。次年，国立大学的A.Lance等首次实验验证了无开关协议［5］。2013年，昆士兰大学的N.Walk等完成了高斯后选择条件下CVQKD协议无条件安全性证明［6］。

1.2 欧洲

法国在CVQKD技术的理论研究与实验技术上代表了当前世界最高水平。2002年，法国高等光学研究所法布里实验室的F.Grosshans和P.Grangier首次提出基于高斯调制相干态和平衡零差检测的CVQKD协议——GG02协议［7］。GG02协议是首个现有技术条件下切实可行的CVQKD协议，是当前最主流的CVQKD协议。2002年，F.Grosshans等改进了CVQKD协议数据协调算法，首次提出了反向协调思想，解决了正向协调算法的3dB极限问题［8］。2003年，F.Grosshans等提出了CVQKD协议的纠缠等价模型(见图1)，建立了CVQKD协议安全分析理论框架［9］。

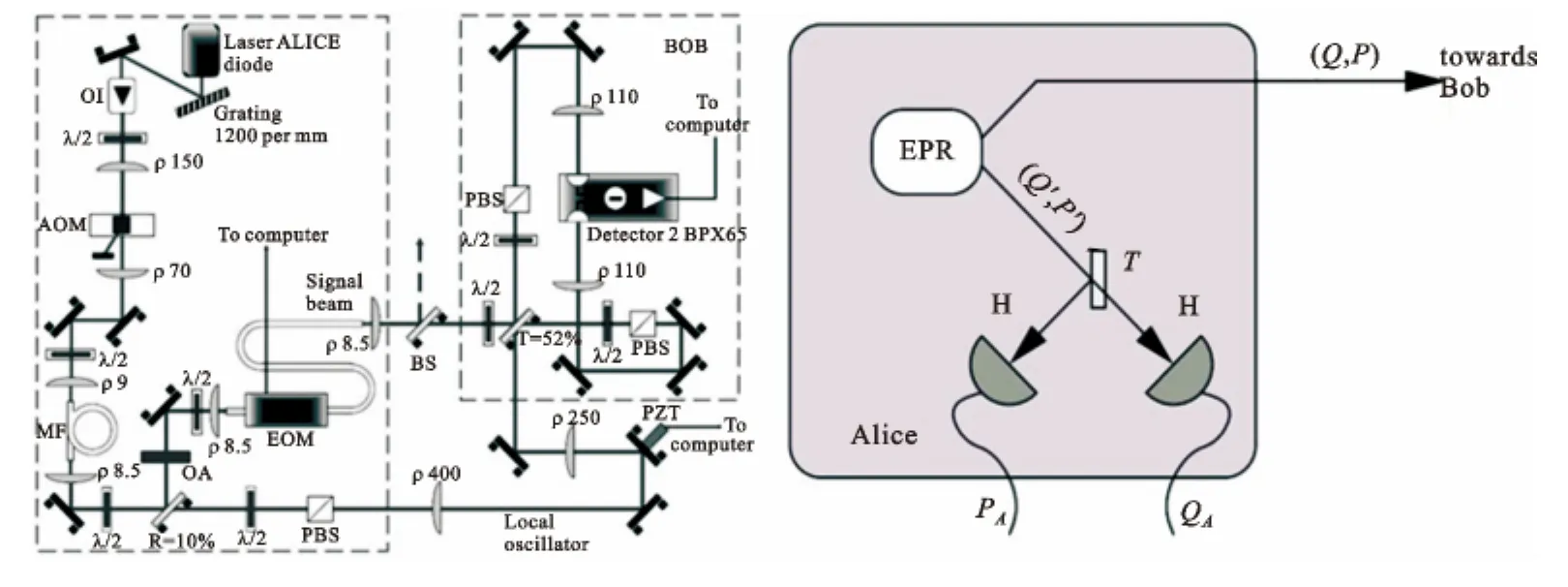
图1 GG02协议的自由空间演示实验和纠缠等价模型

2003年，法国法布里实验室与比利时布鲁塞尔自由大学合作，首次实验实现自由空间信道GG02协议CVQKD系统(见图1)［10］，该成果发表于《Nature》。2005 年，法布里实验室的 J.Lodewyck等设计了基于光纤信道的CVQKD系统方案，为实现CVQKD技术的光纤网络化做出了大胆尝试［11］。2007年，J.Lodewyck等实验演示了25公里全光纤GG02协议CVQKD系统，系统采用了时分复用的方式将本振光和信号光在同一光纤信道中传输，并利用高效LDPC码来实现实时的数据反向协调，系统的重复频率为500 KHz，安全码率 2.2kbit/s［12］。2009 年，法布里实验室的S.Fossier等进行了CVQKD系统外场测试，该系统采取时分复用和偏振复用并用技术，利用LDPC码实现反向协调，并通过自动反馈控制技术调节系统稳定性，在15公里的光纤信道中生成8kbit/s的量子密钥，稳定运行时间达57小时［13］。

2011年，巴黎高等电信研究院的A.Leverrier等针对低效率连续变量密钥协商算法严重影响CVQKD安全传输距离的问题，首次提出高效多维协商算法［14］。随后，A.Leverrier等又提出基于离散调制的CVQKD协议——四态协议，大大缓解了协调效率对CVQKD系统的限制［15］。2012年，巴黎高等电信研究院的P.Jouguet等分析了非理想高斯调制，探测器校准误差、激光器相位噪声等实际非理想因素对系统性能的影响［16］，并设计实现了基于CVQKD技术的点对点对称加密链路，在17.7公里的光纤信道中稳定运行时间长达六个月［17］。同年，法布里实验室的R.Blandino等指出，在反向协调下，新型线性无噪光放大器(NLA)可提升基于高斯调制相干态的CVQKD协议的安全距离和噪声抗性，这无疑对CVQKD技术的推广具有重要意义［18］(见图2)。

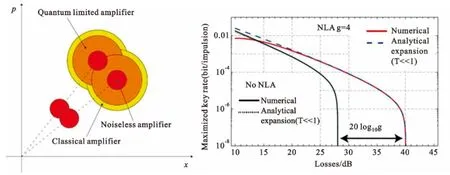
图2 线性无噪光放大器及其对CVQKD的改善作用

2013年，P.Jouguet等大幅度改善了GG02协议CVQKD系统(见图3)，利用多维协商算法和GPU技术将CVQKD系统的数据协调效率提高到95%左右，进而将光纤CVQKD系统实验传输距离大幅提升至80公里，在此传输距离下安全码率接近1kbit/s［19］。

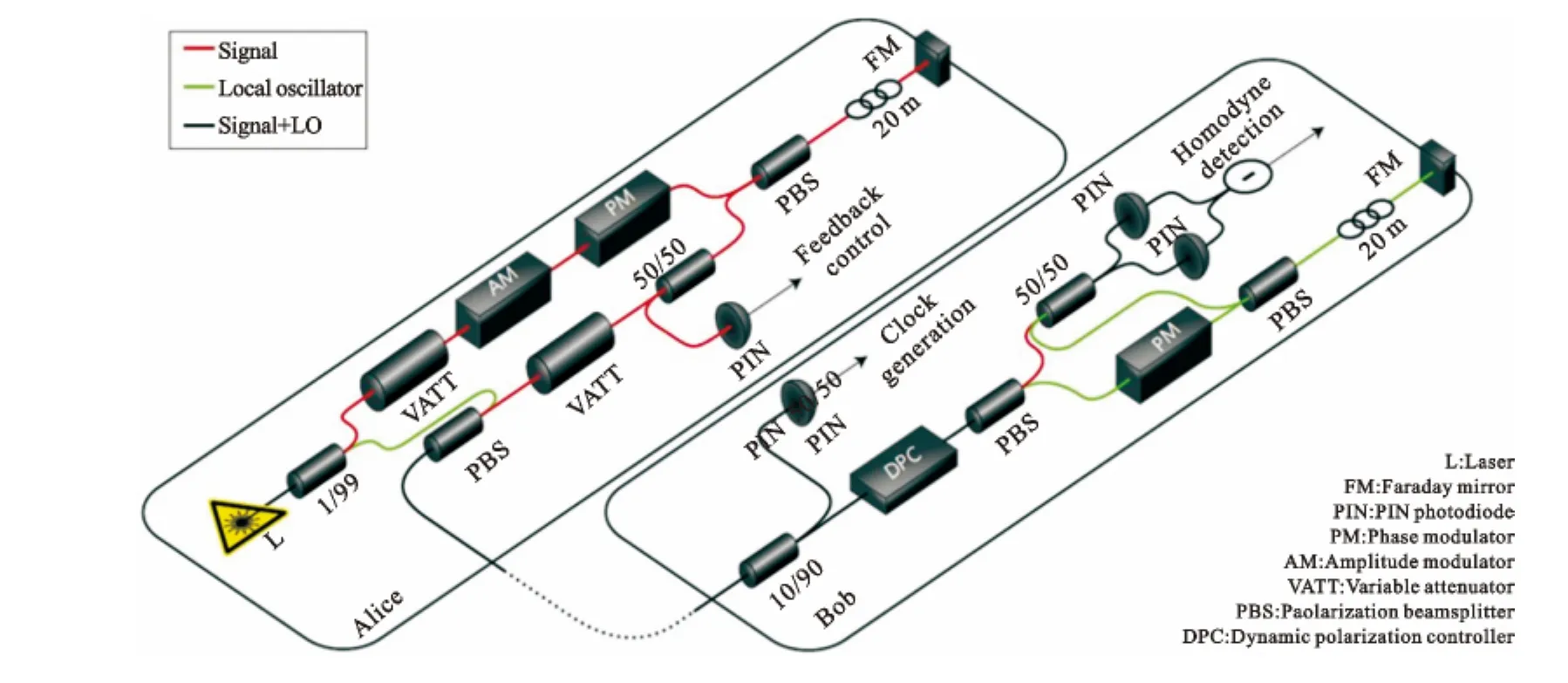
图3 长距离CVQKD传输实验原理图

1.3 加拿大

2007年，加拿大多伦多大学Bing Qi等实验实现了全光纤信道GG02协议 QKD 系统［26］。2011年，该团队 Y.Chi等对CVQKD系统的平衡零差探测器的噪声分析与设计实现做出了详尽的论述［27］。2012年，C.Weedbrook等设计了基于热场态的CVQKD协议，分析了微波频段CVQKD技术的可行性［28］。随后，C.Weedbrook证明了当纠缠源不受合法通信方控制时，CVQKD协议的安全性依然可以保持［29］。

1.4 美国

美国的CVQKD成果报道主要集中于2010年之前。近年来，美国对包括单光子技术在内的所有QKD技术都极少报道。据分析，美国很可能已经开展了QKD技术的实际应用。

2000年，美国纽约城市大学亨特学院的M.Hillery首次提出了一个基于压缩态的连续载波离散调制的保密通信方案［30］。次年，加州理工的D.Gottesman和微软公司的J.Preskill提出了一种基于压缩态的CVQKD协议，并利用量子纠错码首次证明了CVQKD协议的无条件安全性［31］。

在协议优化方面，麻省理工的S.Pirandola等于2008年首次提出了双路CVQKD协议［34］，大大提高了CVQKD协议可容忍噪声阈值。2009年，乔治亚理工的Q.Xuan等实验实现了光纤信道四态 CVQKD协议，传输距离为24.2公里时安全码率达3.45kbit/s［35］。

1.5 中国

在国内，基于光纤的对连续变量量子密钥分发的研究也在逐渐展开，并在一些理论问题上取得了重要成果，这些成果主要集中在光源噪声的建模、双路量子密钥分发协议、连续变量协议安全性等一些方面。主要研究单位有北京大学、北京邮电大学、上海交通大学和中国科技大学等。

2 连续变量量子保密通信技术发展趋势

受限于发展时间短，当前CVQKD系统的技术成熟度不高，但其在量子态制备、探测以及和经典光纤通讯网络融合方面有更大的发展潜力。2013年，法国的P.Jouguet等人在连续变量系统后处理纠错技术上取得突破，完成了80km的CVQKD实验，充分验证了CVQKD技术的发展潜能，具备了构建城域网能力。同年，CVQKD协议理论安全性证明取得巨大飞跃，Furrer和Leverrier等人严格证明了有限码长条件下高斯CVQKD协议的无条件安全性，为CVQKD技术的应用扫清了障碍。

然而，连续变量量子密钥分发技术要真正走向实际应用，当前面临的主要问题如下:第一、技术成熟度相对较低，性能指标有待提升。尤其是，CVQKD系统的安全码率和传输距离有待提高，与实际应用要求有差距。要真正提升CVQKD系统的实际性能，可从两方面着手——实验技术方面提升光源、调制、探测、稳定控制、后处理等关键器件模块的性能指标，理论研究方面改进协议、数据后处理方法以提升协议性能。CVQKD系统性能在很大程度上取决于协议优化和数据后处理理论的进展，如采用后选择技术或提升数据协调的效率和速率等都可有效提升系统性能。现阶段从协议层面、理论层面提出改进，优化协议数据后处理方法等对提升CVQKD系统性能十分重要。第二、实际安全性有待进一步提升，针对量子黑客攻击的防御手段不足。CVQKD协议在理论上被证明具备无条件安全性，但并不完全等价于实际CVQKD系统的安全性。研究实际CVQKD系统的安全漏洞及相应的量子黑客攻防，对保证CVQKD系统的实际安全性具有重要意义。上述两点是现阶段制约CVQKD发展的瓶颈问题，是当前CVQKD领域的学术研究热点，也代表着CVQKD技术现阶段的发展趋势。

此外，相对于业界领先的法布里实验室，国内研究单位基本具备了部分关键技术，但在后处理算法的协调效率、实时性及探测器性能上落后比较明显，需要重点研究和开发，对连续变量量子密钥通信系统的各关键技术进行整体协调和优化、加强工程化研究很有必要。

3 连续变量量子保密通信技术建议

3.1 重视连续变量量子保密通信技术研究

第一，连续变量量子保密通信技术具有良好的发展潜能，是未来量子通信技术必不可少的重要分支。与单光子系统相比，连续变量系统无需单光子源和单光子探测器，大部分器件与经典相干光通信系统通用，具有高重复频率和高密钥速率的发展潜能，在成本和性能方面具有突出优势。第二，连续变量量子保密通信技术近年来发展迅速，可行性得到充分验证，推进其实用化正当其时。第三，连续变量技术与单光子技术可形成优势互补，开展连续变量保密通信技术工程化研究很有必要。2013年，法国法布里实验室将安全传输距离提升到了80公里，该距离虽然对于城际之间的保密通信还稍嫌不够，但对于城市内部重要节点的保密通信来说已经足够。而单光子技术传输距离远，但成本高，适用于城际通信。第四，中国在连续变量量子保密通信系统研发上投入不足，研究水平落后于国外。相对于业界领先的法布里实验室来说，国内研究单位初步具备了各关键技术，主要在后处理算法的协调效率、各关键技术工程化、各关键技术进行整体协调和优化等方面落后。

基于上述原因，我国应抓住当前CVQKD技术的发展热潮，大力开展CVQKD技术研究，占领技术高地。

3.2 加强连续变量量子保密通信系统关键技术研究、整体优化、工程化

要真正做好CVQKD技术，其关键是突破如下关键技术:连续变量量子保密通信系统量子信号产生、传输控制(含偏振态保持、相位漂移补偿、时钟同步及时序对准等)、探测(接近量子极限的高灵敏平衡零差探测技术)以及高效率数据后处理等。

在突破上述关键技术基础之上对系统进行整体协同优化，加强相应工程化研究，将大大推进CVQKD技术的实用化进程。

3.3 加强连续变量量子保密通信实际安全性研究及量子黑客攻防技术研究

QKD的安全性可分为两个层次:理想QKD协议安全性和实际QKD系统安全性。理想QKD协议的安全性是量子密码理论研究的核心内容，是QKD安全性的基石。实际QKD系统是理想QKD协议的物理真实实现。理想QKD协议安全性证明建立在系统物理模块(如光源，编码器，探测器等)的简化数理模型基础之上。实际QKD系统的非理想物理器件往往不完全满足理想模型假设，将导致安全隐患。窃听者可以利用上述安全隐患(或称之为侧信道)窃取信息而不被发现，此即所谓量子黑客攻击(Quantum Hacking Attacks)。如果通信双方忽略系统侧信道，则实际QKD系统的安全性不能得到完全保障。真实的QKD系统只有经过深入的量子黑客攻防研究后，才能确保实际安全性，此研究是QKD走向实用化的必由之路。设计现有技术条件下切实可行的量子黑客攻防技术，是当前的学术研究热点。同时，此项研究是制定实际QKD系统安全标准的重要依据，欧盟已率先开展此项工作。

针对单光子技术，人们已经深入开展了实际安全性及量子黑客攻防技术研究，如光子数分离攻击、相位重映射攻击、非可信光源攻击、多激光器侧信道信息泄露、时移攻击、伪态攻击、探测致盲攻击等量子黑客攻击。而在CVQKD研究中，相应研究处于起步阶段，应着重加强研究。

3.4 加强连续变量量子保密通信后处理技术研究

在CVQKD系统中，量子态传输结束后，发送方和接收方需要通过后处理来生成安全密钥。后处理包括基选择，参数估计，数据纠错、私钥放大四个步骤。其中，数据纠错一直是技术难点和核心。高斯连续变量误码纠错对系统性能影响体现在如下方面:第一，连续变量数据纠错效率大大限制CVQKD系统的安全码率和传输距离。随着通信距离变长，接收方接收到的量子态幅度变弱，信噪比低(约0.1)，误码率增高(可达20%—30%)，数据协调的效率降低(仅约80%)，直接减小系统安全码率。尤其是，通信双方的互信息量与窃听者所获取的信息量大小比较接近，低纠错效率将直接导致系统码率为零。所以，研究低信噪比下高斯随机变量纠错技术是连续变量QKD系统的核心关键问题之一。第二，纠错算法的方向对连续变量QKD系统性能影响重大。根据纠错方向的不同，CVQKD系统的后处理过程可分为正向协调和反向协调。如果系统采用正向协调，则当量子信道的传输损耗大于3 dB时(即通信距离≧15 km时)，连续变量QKD系统的安全码率为0，被称为3 dB极限。正向纠错使用范围较窄，当通信距离较长时必须选用反向纠错。第三，连续变量QKD系统数据纠错速率是限制连续变量QKD系统工作频率的最重要因素。经过长距离传输后，接收方接收到的量子态幅度很弱，信噪比降低，误码率增高，必须选取比较特殊和复杂的纠错算法对其进行纠正，故纠错所需计算资源增加，极大影响了后处理的实时性。

高效率、高速、实时的数据后处理模块，是提升CVQKD系统性能的最有效手段之一，应着重研究。

4 结语

连续变量量子保密通信技术具有良好的发展潜能，是未来量子保密通信技术必不可少的重要分支。受限于发展时间较短，当前CVQKD技术成熟度相对较低，性能指标有待提升。通过进一步加强连续变量量子保密通信系统量子信号产生、传输控制(含偏振态保持、相位漂移补偿、时钟同步及时序对准等)、探测(接近量子极限的高灵敏平衡零差探测技术)以及高效率数据后处理等关键技术，并开展整体优化和工程化研究，连续变量量子保密通信技术有望真正走向实用。

［1］ Ralph T C.Continuous variable quantum cryptography［J］.Physical Review A，2000(61):334－458.

［2］ Ralph T C.Security of continuous－variable quantum cryptography［J］.Physical Review A，2000(62):1125－1136.

［3］ Reid M D.Quantum cryptography with a predetermined key using continuous－variable Einstein－Podolsky－Rosen correlations［J］.Physical Review A，2000(62):495－503.

［4］ Weedbrook C，et al.Quantum cryptography without switching［J］.Physical Review Letters，2004(93):100 －118.

［5］ Lance A M，et al.No－switching quantum keydistribution using broadband modulated coherent light［J］.Physical Review Letters，2005(95):236 －252.

［6］ Walk N，et al.Security of continuous － variable quantum cryptography with Gaussianpostselection［J］.Physical Review A，2013(87):21－34.

［7］ Grosshans F，Grangier P.Continuous variable quantum cryptography using coherent states［J］.Physical Review Letters，2002(88):1246－1252.

［8］ Grosshans F，Grangier P.Reverse reconciliation protocols for quantum cryptography with continuous variables［J］.arXiv:quant－ph，2002(0204127):813－825.

［9］ Grosshans F，et al.Virtual entanglement and reconciliation protocols for quantum cryptography with continuous variables［J］.Quantum Information ＆ Computation 3，2003(535):45－61.

［10］ Grosshans F.Quantum key distribution using gaussian－modulated coherent states［J］.Nature，2003(421，238):331 －352.

［11］ Lodewyck J，et al.Controlling excess noise in fiber－ optics continuous－variable quantum key distribution［J］.Physical Review A，2005(72):440－451.

［12］ Lodewyck J，et al.Quantum key distribution over 25 km with an all－fiber continuous－variable system［J］.Physical Review A，2007(76):523－531.

［13］ Fossier S，et al.Field test of a continuous－variable quantum key distribution prototype［J］.New Journal of Physics，2009(11):1011－1023.

［14］ Leverrier A，et al.Multidimensional reconciliation for a continuous－ variable quantum key distribution［J］.Physical Review A，2008(77):771－780.

［15］ Leverrier A，Grangier P.Unconditional security proof of long－distance continuous－variable quantum key distribution with discrete modulation［J］.Physical Review Letters，2009(102):172－187.

［16］ Jouguet P，et al.Analysis of imperfections in practical continuous－ variable quantum key distribution［J］.Physical Review A，2012(86):182－191.

［17］ Jouguet P，et al.Field test of classical symmetric encryption with continuous variables quantum key distribution［J］.Optics Express，2012(20，14030):153－162.

［18］ Blandino R，et al.Improving the maximum transmission distance of continuous－variable quantum key distribution using a noiseless amplifier［J］.Physical Review A，2012(86):1701－1712.

［19］ Jouguet P，et al.Experimental demonstration of long－distance continuous－variable quantum key distribution［J］.Nature Photonics，2013(7，378):431－440.

［20］ Cerf，N J，Levy M，VanAssche G.Quantum distribution of Gaussian keys using squeezed states［J］.Physical Review A，2001(63):51－59.

［21］ Garcia － Patron R，Cerf N J.Unconditional optimality of Gaussian attacks against continuous－variable quantum key distribution［J］.Physical Review Letters，2006(97):610－623.

［22］ Garcia－Patron R，N J Cerf.Continuous－ variable quantum key distribution protocols over noisy channels［J］.Physical Review Letters，2009(102):223 －231.

［23］ Renner R，Cirac J I.de finetti representation theorem for infinite－dimensional quantum systems and applications to quantum cryptography［J］.Physical Review Letters，2009(102):123－127.

［24］ Furrer F，et al.Continuous variable quantum key distribution:finite－key analysis of composable security against coherent attacks［J］.Physical Review Letters，2012(109):256－261.

［25］ Leverrier A，et al.Security of continuous－ variable quantum key distribution against general attacks［J］.Physical Review Letters，2013(110):310 －315.

［26］ QI B，et al.Experimental study on the Gaussian－modulated coherent－state quantum key distribution over standard telecommunication fibers［J］.Physical Review A，2007(76):380－385.

［27］ CHI Y M，et al.A balanced homodyne detectorfor highrate Gaussian－modulated coherent－state quantum key distribution［J］.New Journal of Physics，2011(13):41－51.

［28］ Weedbrook C，Pirandola S.Ralph T C，Continuous－variable quantum key distribution using thermal states［J］.Physical Review A，2012(86):67－78.

［29］ Weedbrook C.Continuous－variable quantum key distribution with entanglement in the middle［J］.Physical Review A，2013(87):106－112.

［30］ Hillery M.Quantum cryptography with squeezed states［J］.Physical Review A，2000(61):634－640.

［31］ Gottesman D，Preskill J.Secure quantum key distribution using squeezed states［J］.Physical Review A，2001(63):551－556.

［32］ Silberhorn C，et al.Continuous variable quantum cryptography:Beating the 3 dB loss limit［J］.Physical Review Letters，2002(89):611 －616.

［33］ Navascues M，Grosshans F，Acin A.Optimality of Gaussian attacks in continuous－ variable quantum cryptography［J］.Physical Review Letters，2006(97):111 －118.

［34］ Pirandola S，et al.Continuous－ variable quantum cryptography using two－way quantum communication［J］.Nature Physics，2008(4，726):20 －27.

［35］ XUAN Q D，ZHANG Z S，Voss P L.A 24 km fiberbased discretely signaled continuous variable quantum key distribution system ［J］.Optics Express，2009(17，24244):71－75.