基于双向运输的集装箱物流系统的优化研究∗
2015-11-02司玉军郑宗浩翁凌韬段国林
司玉军,郑宗浩,翁凌韬,段国林
(1.河北工业大学 机械工程学院,天津,300130;2.曹妃甸港集团股份有限公司 通用码头分公司,河北 唐山,063000)
近年来国内外学者对码头港区内集卡的优化调度做了深入的研究,提出了相应的理论,李广儒等从整体调度的角度出发,应用蚁群算法,分析了整个码头集卡作业面的动态调度方案[1];魏宏磊等以集卡行驶路径最短为优化目标,建立基于装卸同时进行的集卡路径优化模型[2];Ruiyou Zhang等涉及多个集装箱堆场的多发地和多目的地问题,考虑空箱调运,求解集卡运输的最短距离[3];杨静蕾等建立“作业面”下路径优化模型,计算集卡的最优行驶路径[4];Niraj Ramesh Dayama等将集装箱的堆存位置与起重机的调度结合,优化整个作业过程的最小成本[6];俞涛等综合考虑集卡与前沿岸桥和堆场场桥的制约关系,优化集卡的运输路径和最小配置数量[6];王启航等将码头生产作业模式分为三种,以集卡行驶路径最短和码头生产作业成本最低为目标函数建立优化模型[7];Narges Kaveshgar等建立岸桥调度与集卡行驶路径结合的整数规划模型,采用遗传算法求解[8];张银利等着重整个港区与港口腹地的结合,应用遗传算法,建立集卡调度优化模型,求解港口到经济腹地的优化路径[9];Daganzo CF等针对装卸设备的优化配置研究做了优化[10];上述这些研究为集装箱码头的实际生产运营提供了一定的支持,推动了码头效率的提高,但由于码头实际作业条件制约造成理论适用性不强,主要原因是建立理论模型时将很多实际因素量化甚至忽略导致与港口实际情况不符,本文综合考虑道路通行能力的限制约束,建立混堆模式下装卸同时进行的港口集卡路径优化模型,对港口运营效率的提高更具有实际意义.
1 基于优先级别属性的集装箱堆取方案设计
进口箱在堆场的堆存时间一般不超过三天,按堆存天数划分为三级,属性值为1、2、3.考虑内陆客户的运营成本,方便客户提箱,保持港方与客户间的良好关系,将客户离堆场距离的远近分为三级,属性值为1、2、3.两种属性相乘得出进口箱的综合属性值.对于出口箱,考虑船舶的稳定性,重箱放下面轻箱放上面,使船舶重心尽可能低,将出口箱按重量级别分为三级,其属性值为1、2、3.由于船舶是班轮运输,针对其卸货港的远近,近距离的放上面,远距离的放下面,防止卸载时翻箱.国内的港口之间距离一般不超过10 000km,国际港口之间的距离在15 000km左右,由此根据卸货港距离分为三级1、2、3.两项属性相乘得出口箱的综合属性值.虽然堆场箱区是混堆模式,但为了提箱方便,同一箱区内进出口箱一般也是分开堆放,所以进口箱与出口箱的属性一般不同且不能交叉比较.箱区的属性值取不同集装箱属性值的综合平均值.船舶上的进口箱卸箱时,如果进口箱的属性值小于等于箱区的综合属性值,那么就可以在该箱区堆存,同理对于装载到船舶的出口箱同样遵循属性值低的集装箱压属性值高的集装箱的原则,见表1、表2.
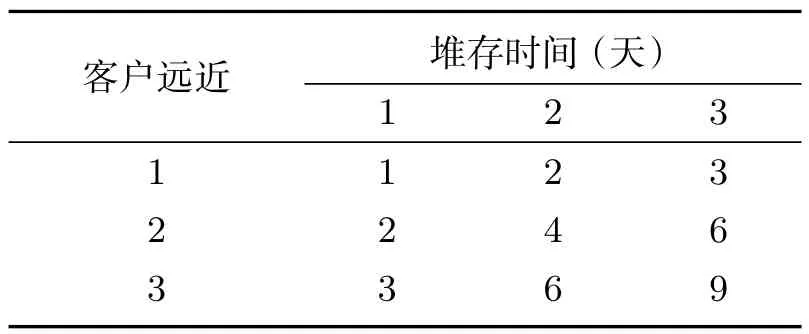
表1 进口集装箱属性表
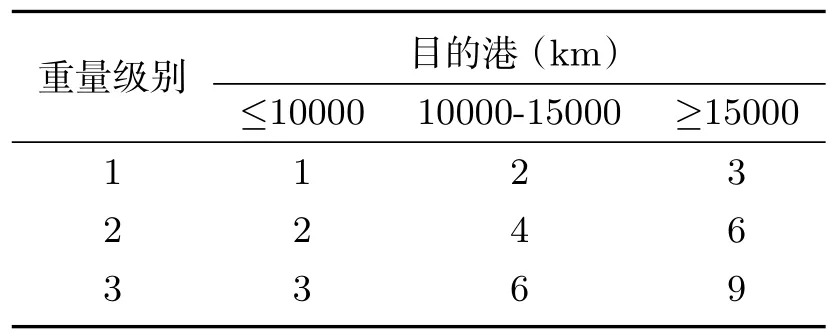
表2 出口集装箱的属性表
2 基于码头集装箱堆取方案下的集卡路径优化模型
2.1 集卡运输过程中道路限制问题
以往堆场内集卡路径的研究没有考虑到道路通行量的限制,造成实际中集卡运输集装箱时某一路线上运输的集卡数量太多造成道路拥挤集卡、不得不停车等待.而其他的路线上集卡数量较少造成该路线利用率不高,达不到降低作业成本的效果,反而延长了集卡的等待时间.由于堆场的道路宽度是一定的.决定了道路的通行能力也是一定的.道路通行能力的限制主要分为每条路线上能容纳的最多同时运输的集卡数目和工作班时间内每辆卡车在每条路线上所能运输的最大车次数两个方面.T为一个工作班次;t1为场桥服务一个集装箱的单位时间;t2为岸桥桥服务一个集装箱的单位时间;集卡在箱区i和船舶贝位j间的运输时间为:
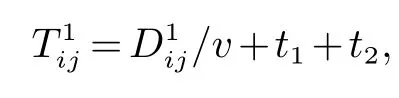
集卡在箱区i和箱区j间的运输时间为:
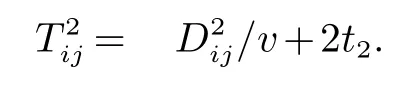
同一时刻岸桥或场桥只能为一辆集卡服务,其他的集卡同时刻只能是在路线上行驶或等待,所以每条路线上同一时刻的集卡数目是受限制的.装箱时箱区i到贝位j作业线路上能容纳的最大集卡数量为:
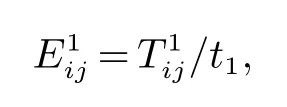
卸箱时贝位j到箱区i作业线路上能容纳的最大集卡数量为:
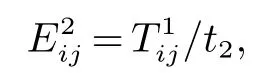
集卡从箱区i到箱区j装载出口箱的作业线路上能容纳的最大集卡数量为:
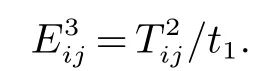
堆场道路是集疏运双向车道,可以分为装箱运输路线车次和卸箱运输路线单独考虑,每条路线上集卡的最大运输车次为工作班时间与岸桥或场桥从开始服务第一辆集卡到服务最后一辆集卡前的时间差再除以集卡在该路线上的运输时间,装箱时集卡从箱区i到贝位j作业线路上最多可以行驶的车次为:
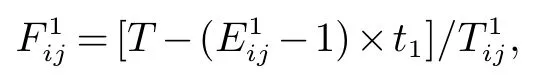
卸箱时集卡从贝位j到箱区i作业线路上最多可以行驶的车次为:
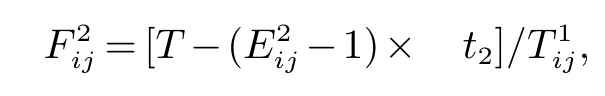
集卡从箱区i到箱区j装载出口箱的作业线路上集卡最多可以行驶的车次为:
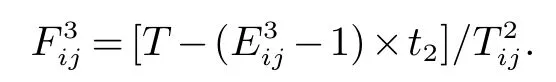
根据集卡在每条运输路线上的数量约束和车次限制可以很好的解决实际运输中的车辆堵塞问题,为集卡的运输路径选择更合适的路线,提高集卡的运输效率.
2.2 模型建立
为了降低船舶的运营成本,装卸箱作业时卸载完集装箱后还要装载部分出口箱,设定堆场各箱区的出口箱数量和船舶中各个贝位将要卸载的进口箱数量已知,船舶到港从卸箱开始,集卡装载进口箱到箱区卸箱后,再行驶到指定的箱区,装载出口箱运往岸边装箱,由此集卡完成一个完整的作业回路.
码头有M个箱区;船舶有N个贝位;为箱区i运往船舶贝位j的出口箱量;为箱区i装载的船舶j的进口箱量;为集卡从箱区i到箱区j装载出口箱的箱量;为箱区i到船舶贝位j的距离;为箱区i到箱区j的距离;C为箱量A与B差值的绝对值,即作业线模式下运载的集装箱量;A为堆场中要装船的出口箱数量,B为船舶上要卸载的进口箱数量;W、Z分别为箱区和船舶贝位的容量;xij为0-1变量,表示箱区i的出口箱是否装载到船舶贝位j上,当出口箱的属性值不超过船舶贝位的属性值时xij为1,否则为0;yij为0-1变量,表示箱区i是否堆存船舶贝位j的进口箱,当进口箱的属性值不超过箱区的属性值时yij为1,否则为0;zij为0-1变量,表示集卡是否从箱区i到箱区j装载出口箱,集卡从箱区i到箱区j装载出口箱则zij为1,否则为0.
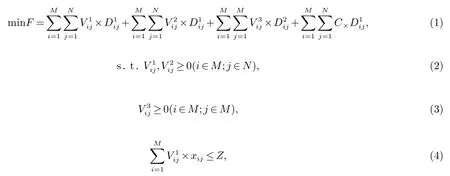
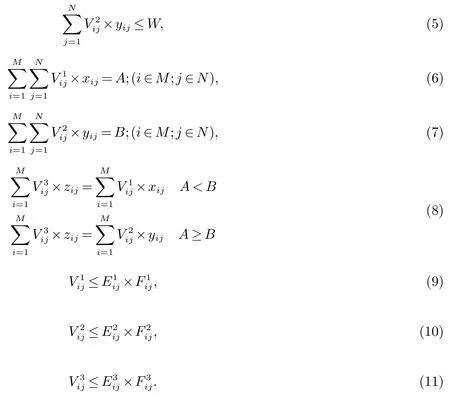
目标函数式为求解集卡总的行驶路径最短,将整个集卡的作业面过程分为4个部分:第1部分为集卡从箱区到船舶贝位运载出口箱过程;第2部分为集卡从船舶贝位到箱区间运载进口箱过程;第3部分为集卡从箱区到箱区运载出口箱的过程;第4部分为进出口箱量不平衡条件下.多余箱量集卡的空载过程,由于集装箱堆场的道路为双向车道,集卡的集疏运道路是独立互不影响的,求解各部分的集卡最短行驶路径,即求得集卡总的最短行驶路径;约束式2和3为正整数约束;约束式4保证卸载的箱区的进口箱数量小于箱区的容量;约束式5为装载到船舶贝位的出口箱数量小于该贝位的容量;约束式6和7表示运完所有的出口箱和进口箱;约束式8为保证作业面模式的约束;其中约束式9装船时从箱区i到船舶贝位j运载的箱量不能超过该作业线路上总的运行车次;约束式10为当卸船时从船舶贝位j到箱区i运载的箱量不能超过该作业线路上总的运行车次;约束式11为集卡从箱区i到箱区j装载的出口箱量不能超过该作业线路上总的运行车次.
2.3 案例分析
当前大部分港口根据卸货港目的的远近确定出口箱在船舶贝位中的具体位置.根据堆存时间的长短确定进口箱在堆场箱区的堆存位置,一般出口箱有出口舱单,进口箱有进口舱单,舱单上有对应的集装箱属性.本文通过集装箱的一些属性制定进出口箱的属性表,根据属性表来确定集装箱堆放位置.
设堆场有9个箱区,到港船舶有6个贝位,集卡的平均行驶速度为20 km/h,岸桥服务一个集装箱的单位时间为3 min,场桥服务一个集装箱的单位时间为2 min;滚动计划方案为每4 h为一个工作班次,即每4 h堆场信息更新一次,具体数据见表3—表7.

表3 各箱区要提走的出口箱量及其综合属性值

表4 各箱区已有箱量的综合属性值

表5 船舶各贝位要卸载的集装箱量及其综合属性值

表6 船舶各贝位现有箱量的综合属性值
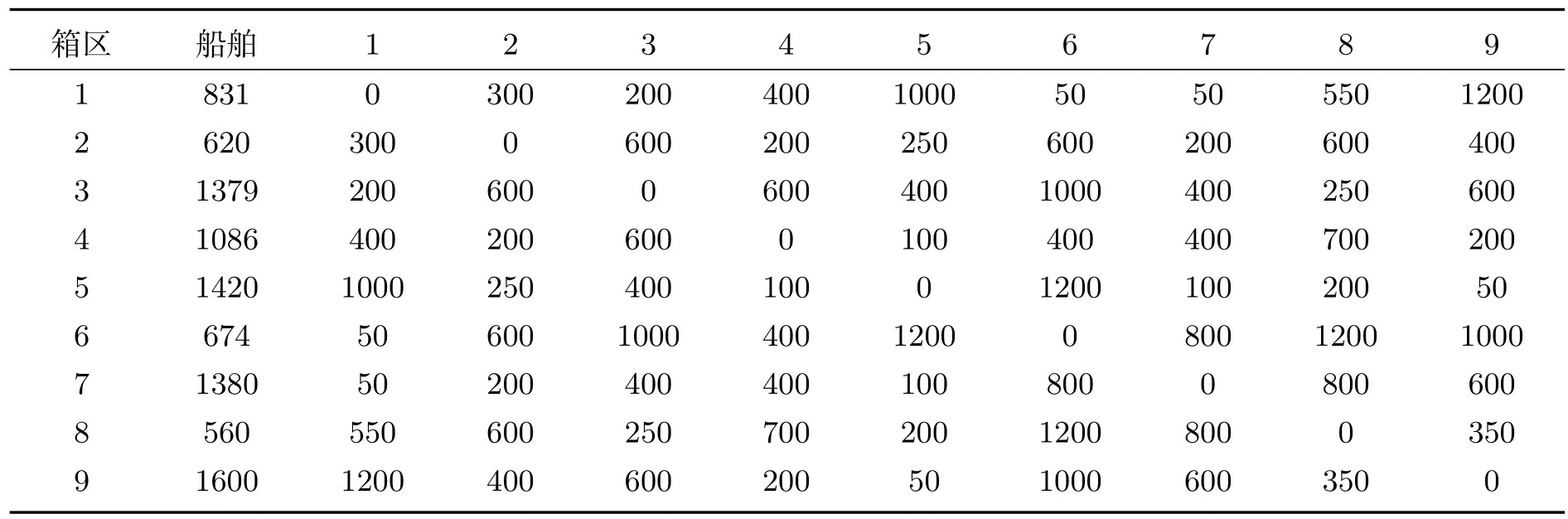
表7 各箱区与船舶的距离及各箱区之间的距离
模型根据以上数据采用Lingo11.0软件求解,可得出进口箱和出口箱分别在堆场和船舶贝位中的堆存位置,以及集卡的数量.
2.4 算例结果分析
应用软件求得目标函数值为1 327 558,即为集卡的最短行驶路径,集卡的最小数量为12;根据集装箱的属性表,由模型优化结果可得作业线下的运输集装箱量为集卡从箱区4的74个出口箱运到船舶贝位3,箱区8的45个出口箱运到船舶贝位3,箱区3的152个出口箱运到船舶贝位2,作业面下的具体运输路径见表8.进口箱和出口箱分别在船舶贝位和各箱区的堆存位置见表9、表10.
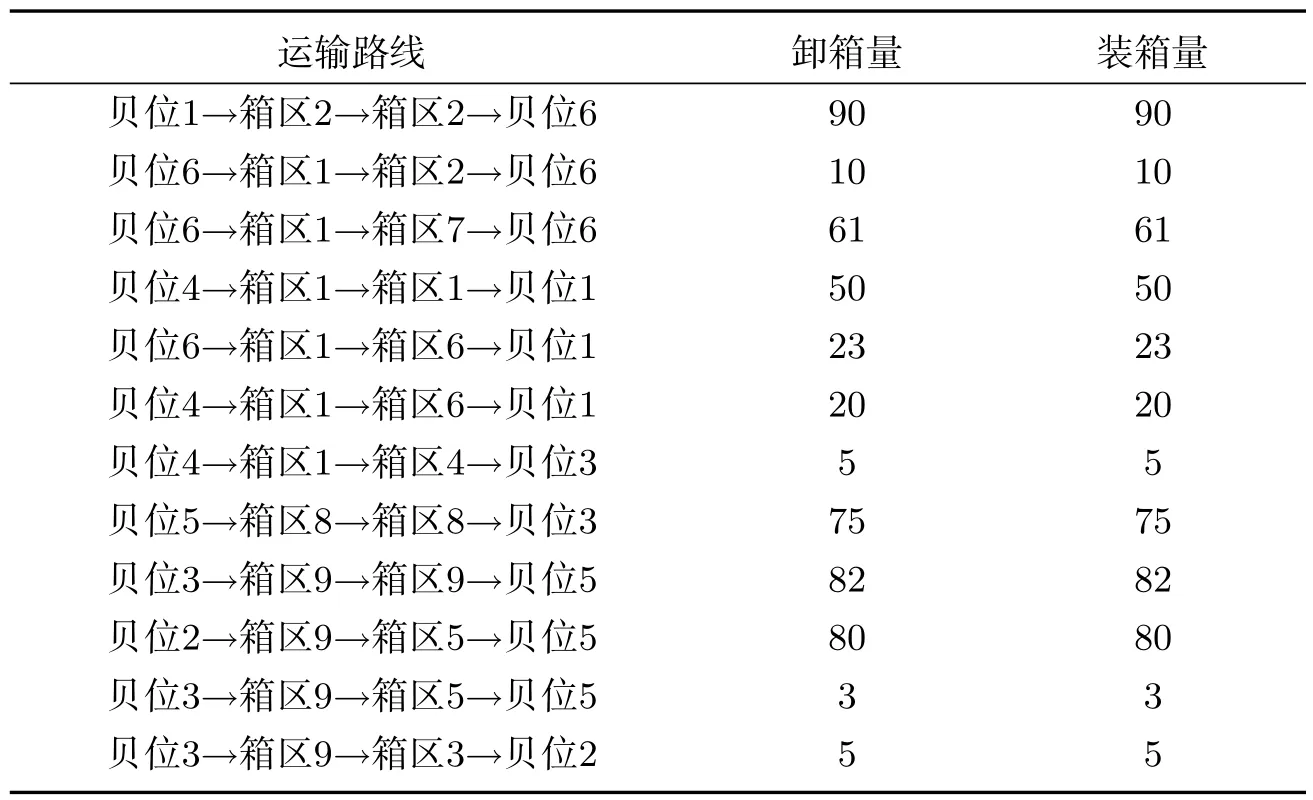
表8 作业面下集卡的运输路径
3 结语
本文针对整个堆场进出口箱的物流过程,从船舶到港装卸作业开始到结束,对整个流程内集卡的作业过程和集装箱堆放过程等做了详细的分析,建立了相应的模型,并通过算例验证了模型的有效性和可靠性,其研究结论如下:
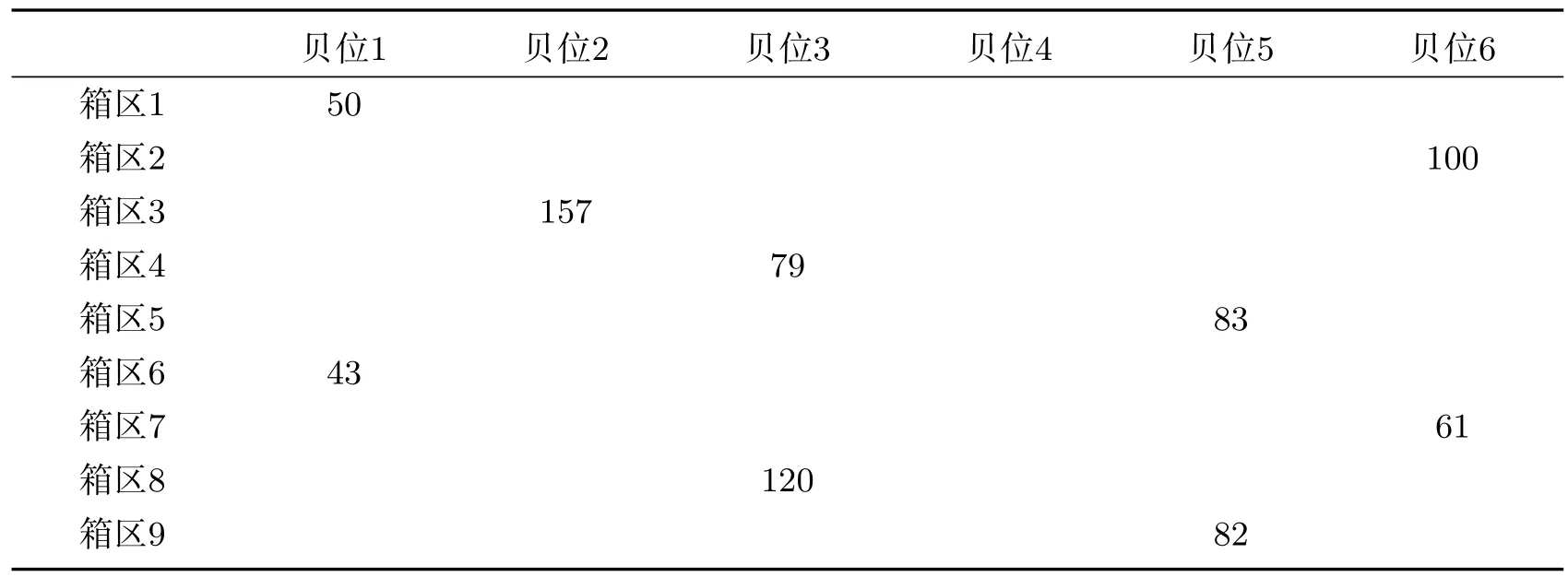
表9 各箱区向船舶各贝位运输的出口箱箱量
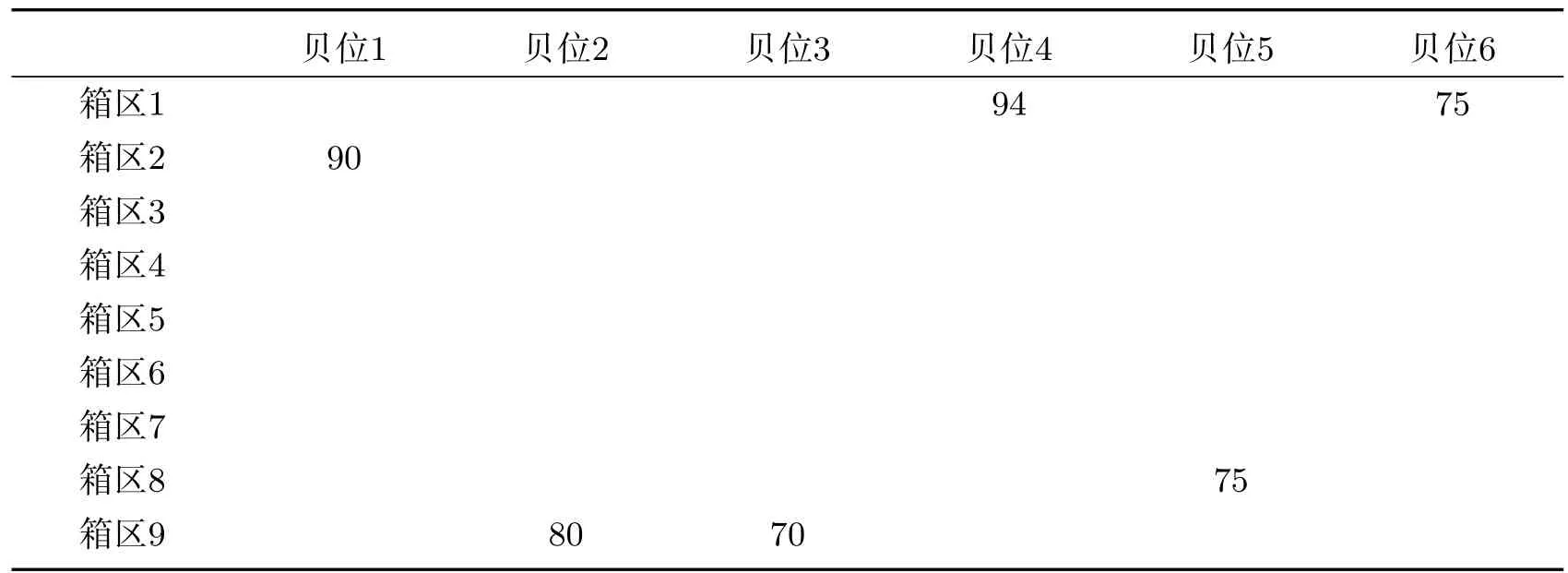
表10 各箱区堆存的船舶各贝位的进口箱量
1)根据集装箱的相关信息建立属性值,通过属性值的大小集装箱与箱区或者船舶贝位的属性做比较确定其堆放位置;
2)充分考虑了道路约束的限制,给出了每条车道的最大容量和能通过的最大车次,更符合码头本身实际情况;
3)结合上述两点,建立的混堆模式下的优化模型,不仅求得了各箱区和船舶贝位各自的堆存量,同时确定了集卡的最少配置数量,并可以通过进一步的分析可以得出集卡的行驶路径.
