双值约束三次规划问题的全局最优性充分条件

叶 敏

(康居西城小学，重庆401331)

1 基础知识

三次规划问题有许多实际应用，比如金融、农业、组合证券投资选择等方面［1－3］.吴至友［4－5］等人提出了一种研究全局最优性条件的新方法—L-次微分法来对一些特殊的非凸二次规划问题的全局最优性充分条件进行研究，并得到了一些初步的研究成果.L-次微分与一般凸函数的次微分不同，一般凸函数的次微分是由一些线性函数组成的集合，而L-次微分可能是由一些非线性函数组成的集合.2010年，Wang等在文献［6］中利用文献［5］中所提出的抽象次微分为工具，建立了带箱子或二元约束的三次规划问题的全局最优性充分和必要条件;2012年，Zhang等在文献［7］中研究了一些带箱子或二元约束的一类特殊三次极小化问题的全局最优性充分条件.此处利用拉格朗日函数和L-次微分的方法，给出了双值约束的三次极小化问题的全局最优性充分条件，而且得到了此类三次规划问题在一些特殊情况下的结果，此结果与文献［7］中的相应结论是一致的.同时给出例子说明给出的最优性条件能有效地用于确定给定的三次极小化问题的全局极小值，所得结果改进和推广了文献［7］中的相应结果.

考虑如下三次规划问题:

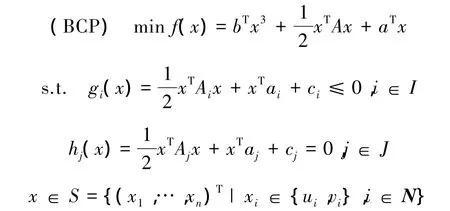
其中 ui，vi∈R，ui＜vi，i=1，2，…，n，b=(b1，…，bn)T∈Rn，a∈Rn，A∈Sn，Sn是所有 n×n 对称矩阵的集合，).为了方便讨论，不妨令 N={1，2，…，n}，I={1，2，…，m}，J={m+1，…，m+p}.

在文中，令L为一些特殊的三次函数组成的集合:

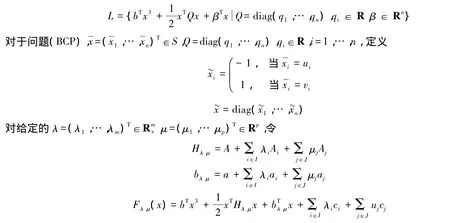
2 主要结果

在下面的证明中令L为如下二次函数组成的集合:

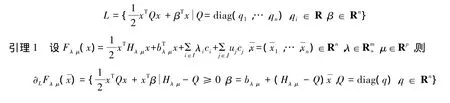
由引理1可以得到下面关于问题(BCP1)的全局最优性充分条件.

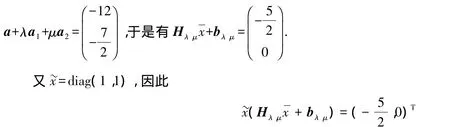
［1］HANOCH G，LEVY H.Efficient Portfolio with Quadratic and Cubic Utility［J］.JBus，1970(43):181-189

［2］LEVY H，Sarnat M.Investment and Portfolio Analysis［M］.New York:Wiley，1972

［3］HENIN C，DOUTRIAU J.A Specialization of the Convex Simplex Method to Cubie Programming［J］.Decis Econ Finance，1980(3):61-72

［4］WU Z Y，JEYAKUMAR V，RUBINOV A M.Sufficient Conditions for Global Optimality of Bivalent non-convex Quadratic Programs with Inequality Constraints［J］.JOptim Theory Appl，2007，133(1):123-130

［5］JEYAKUMAR V，RUBINOV A M，WU Z Y.Non-convex Quadratic Minimization Problems with Quadratic Constraints:Global Optimality Conditions［J］.Math Program A，2007，110(3):521–541

［6］WANGY J，LIANGZ A.Global Optimality Conditions for Cubic Minimization Problem with Box or Binary Constraints［J］.JGlob Optim，2010，47(4):583–595

［7］JEYAKUMAR V，LEE G M，SRISATKUNARAJAH S.Distinguishing a Global Minimizer from Local Minimizers of Quadratic Minimization with Mixed Variables［J］.Pac JOptim，2010(6):65-74

［8］LI G Q，WU Z Y.Global Optimality Conditions for Mixed Integer Quadratic Programming Problems［J］.Math Appl，2011，24(4):845-850

［9］ZHANG X M，WANG Y J，MA W M.Global Sufficient Optimality Conditions for a Special Cubic Minimization Problem［J］.Math Probl Eng，2012(2012):1-16

［10］ZHOU X G，CAO B Y.New Global Optimality Conditions for Cubic Minimization Subject to Box or Bivalent Constraints［J］.Pac JOptim，2012(8):631-647