改进的局部泛化误差模型及其在特征选择中的应用
2015-11-02马艳东
马艳东
改进的局部泛化误差模型及其在特征选择中的应用
马艳东
神经网络的性能可以通过泛化误差表达。泛化误差越小,则说明该神经网络在未知样本中的预测能力越强。反之,说明该神经网络的预测能力很差。对Wing W.Y. NG等人提出了局部泛化误差模型进行了改进,并将新模型应用到特征选择当中。试验结果表明,相对于原有模型,该模型具有更贴近实际的对泛化能力进行表达的能力。
在模式识别率领域,泛化误差模型能够描述分类器对未知样本进行准确分类的能力,也是近几年来的研究热点。一般的泛化误差模型都是以包括未知样本的整个样本空间为基础进行研究的。但是,Wing W.Y. NG等人却另辟蹊径提出了局部泛化误差模型(Localization Generalization Error model,L-GEM)。该模型认为对距离已知样本距离过远的样本考虑泛化能力没有任何意义。故而将考虑范围误差模型的基础更正为值考虑距离已知样本距离较近的空间。这样获得局部泛化误差模型不仅降低了模型推导的难度,而且,具有更贴近实际的意义。然而,通过研究发现,该局部泛化误差在推导过程与理论基础上面出现了些许错误。比如在推导局部泛化误差模型的上限过大,而且推导的理论依据也不是很坚实。本文提出了一种新型的基于范数的局部泛化误差模型(Normbased Localization Generalization Error model,NL-GEM)。该模型不仅避免了原L-GEM模型的推导过程中出现的错误,而且具有更简单的推导过程与更易于理解的理论基础。
基于范数的局部泛化误差模型
Q近邻
对于任意给定的训练样本xb,可以找到一个训练样本集,满足

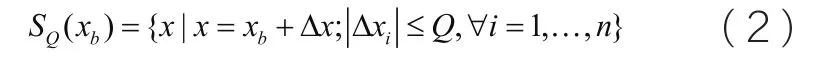
令SQ为所有SQ(xb)的并集。
局部泛化误差模型
假定将计算泛化误差的考虑控件限定在Q近邻的范围内,则局部泛化误差模型L-GEM的推导过程简单描述如下。
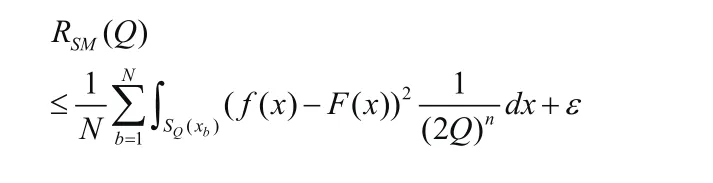
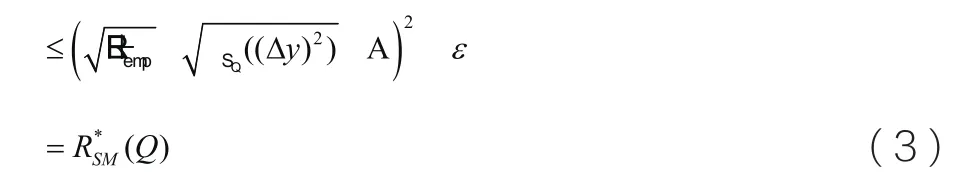
其中,fθ(x)是分类器的真实输出。F( x)为分类器的期望输出。θ从域Λ中选择出来的一组参数集。 A为目标输出最大值与最小值之差。
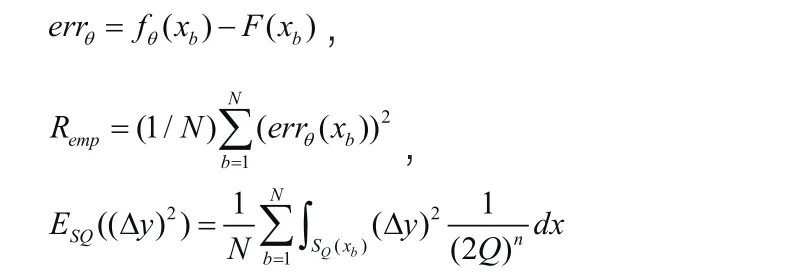
基于范数的局部泛化误差模型(NL-GEM)
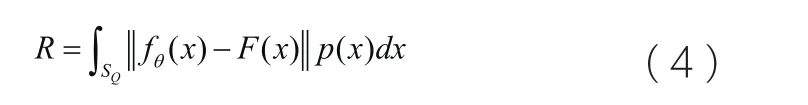
NL-GEM模型的推导过程如下:

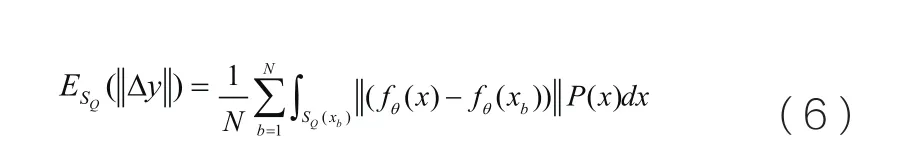
公式(5)的第2项:
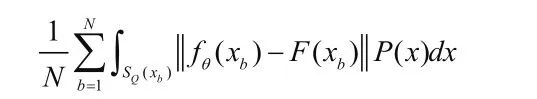
是训练集的训练误差,用Remp表示。因此,公式(5)则可以简写成:
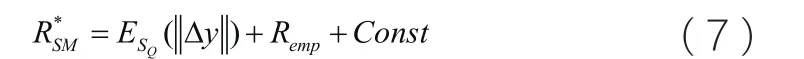
这就是NL-GEM模型的最后推导形式。对比LGEM模型,该模型具有以下三项优点。第一:该模型的推导过程比L-GEM的推导过程更加坚定;第二:该模型更加利于理解与计算。第三:理论基础更加坚实。
NL-GEM模型在特征选择中的应用
对于训练RBF(Radial Basis Function)神经网络的需求来说,输入数据的维数并不是越多越好。而且数据维数越多,存储需要的空间也越多。处理数据花费的成本也越多。更有甚者,数据维数多到一定程度,RBF神经网络的性能还会有明显的下降。而特征选择可以帮助RBF神经网络利用更少但更加代表数据本质的特征,训练出性能不比使用所有特征训练的网络的性能差,甚至更好的分类器。
SM神经网络来说是不重要的。
步1:初始化IFS为全部特征的集合;
步2:利用IFS里的特征,训练RBF神经网络;
步5:如果终止条件没有满足,则跳转到步2。
终止条件一般为:测试误差下降的较快,或者,RBF神经网络的性能满足要求,或者,IFS只包含一个特征。在步2中,采用两阶段发来训练RBF神经网络。 第一阶段,利用K-mean聚类算法计算隐含层节点的中心与宽度。第二阶段,伪拟的方法计算网络的权重。
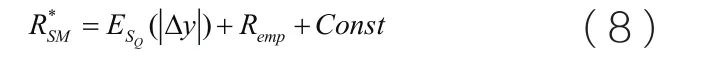
仿真实验
下面对本文提出的算法进行仿真实验,试验数据特选取UCI机器学习数据库中的Iris、Glass数据集,作为样本集。其中Iris具有150个样本数,4个特征,3个类标。Glass数据集则有214个样本,9个特征,6个类标。为验证本算法的可行性,进行特征选择对比试验。分别对上述2个数据集重复进行10仿真实验,取其识别精度的平均值作为其训练与测试能力的评价标准。在针对Iris数据集进行试验时,RBF神经网络的隐含层结点数目为6。针对Glass数据集进行试验时,RBF神经网络的隐藏层节点数目为21。
仿真实验结果如表1与2所示。
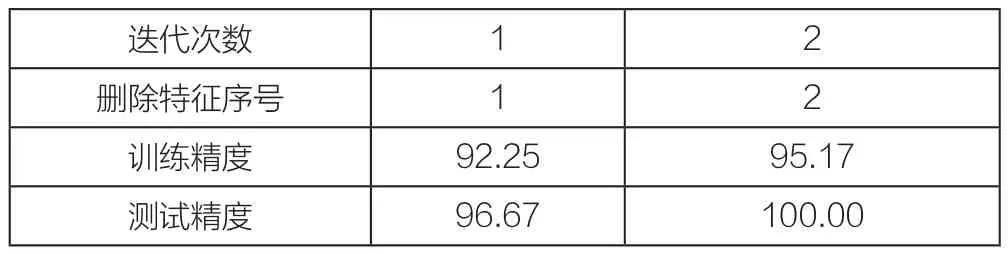
表1 Iris数据集的特征选择结果
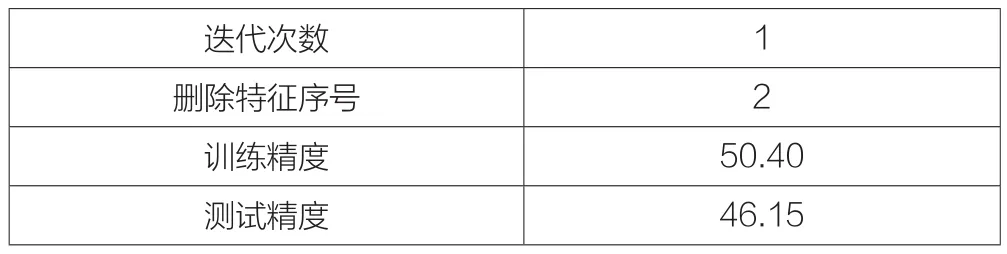
表2 Glass数据集的特征选择结果
由表1可知,针对Iris数据集,当在第2此迭代时,在分别删除第1与2个特征之后,RBF神经网络的训练精度提高了近3个百分点。而测试精度达到了100%。
由表2可知,针对Glass数据集,如果任意删除其中的一个特征后,RBF神经网络的训练精度与测试精度都会有极大幅度的下降。因此,对Glass数据集来说,所有的特征都是重要的特征。
结语
关于未来工作,将在更多的数据集上验证该模型的可行性。还会利用均方误差模型实现该模型。也会尝试其他方法来降低该模型的复杂度。最后还会将该模型应用到其他领域,如结构选择、激励学习等。
10.3969/j.issn.1001-8972.2015.10.013