一种改进遗传算法在孔群加工路径中的优化*

肖军民

（中山职业技术学院机电系，广东中山 528404）

一种改进遗传算法在孔群加工路径中的优化*

肖军民

（中山职业技术学院机电系，广东中山 528404）

数控加工中心采用钻削或铰削方式加工孔群时，为了缩短加工中心刀具空走行程并提高孔群的加工效率，须对孔群加工路径进行优化。数控加工中心孔群加工路径优化属于NP完全问题，到目前为止还没有一个非常有效的算法能求解出NP问题的最优解。针对数控孔群加工路径具体优化问题，采用了一种整数染色体的遗传算法，这种遗传算法以孔号为染色体，采用“优胜劣汰”的生物进化方法寻找问题的最优近似解。经过实例证明该方法的求解精度高于粒子群和蚁群等其它智能优化算法，因此改进的整数染色体遗传算法能较好地解决孔群加工路径优化问题。

遗传算法；孔群加工；路径优化；数控加工；NP完全问题

0　引言

由于目前所有数控自动编程软件都没有孔群加工路径优化模块，所以数控编程人员都是凭借自己的经验随机地确定各个孔的加工顺序。而在数控钻削或铰削加工中，孔群加工的比重大，由编程人员随机确定孔群的加工路径难以实现对路径的优化，在批量生产中这将极大影响生产效率。因此优化孔群加工路径，缩短加工中心刀具在XY平面的空行程距离，将有助于提高生产效率和节省能耗。孔群加工路径的优化是CAM中需要首先解决的问题，是目前的一个研究热点［1］。孔群加工路径优化是典型旅行商问题（Travelling Salesman Problem，TSP），其解空间存在“组合爆炸”。该问题理论上可以获得精确解，但对于大规模节点，这种精确解法将耗时巨大，难以满足工程中实际的应用［2］。TSP问题都属于组合数学中的NP完全问题，属于世界性的难题。该问题随着节点数的增加，其求得理论最优值所需的计算量便呈几何级数增长，如当节点数为200时，每秒计算数亿次的大型计算机仍需要10358年才可能求得最优解［3］。因此对于TSP问题人们已提出了许多常见的近似解法，如最邻计算法、最小树加权近似法、插入法和多边交换调整算法等，这些传统的最优近似解法虽然可以获取相关问题的近似解，但是由于它们方法本身的缺陷有可能导致近似解与理论最优解偏差较大，甚至远离最优解。近年来，一些智能优化方法被用于TSP问题求解，如蚁群算法［4］、粒子群算法［5-6］、遗传算法［7］和模拟退火算法等［8］。作为一种随机搜索算法，遗传算法借鉴了生物进化的遗传机制，通过“优胜劣汰”的选择、交叉和变异等基本操作搜索问题的最优解。遗传优化算法实现比较简单，求解过程中不需要导数信息，鲁棒性强，且具有并行计算的能力，空间搜索能力强［9］。因此运用遗传算法求解孔群加工路径优化问题，可有效处理CAD中的数据，并能使得孔群加工的效率有较大幅度的提高。本文提出的基于整数染色体遗传算法能较好地处理孔群编码问题，并通过改进算法能避免遗传算法早熟收敛等缺点，通过具体的实例求解，可以证明本文提出的遗传算法求解精度高于粒子群和蚁群等其它智能优化算法。

1　问题模型描述

型进行表示，具体如下：G=（V，E）是一个带正权的完全图，V是完全图的顶点集合，V=｛V1，V2，…，Vn｝，n为孔群内孔的数量，Vi为顶点集合中第i个位置孔的编号，E表示边的集合，边（i，j）的权值记为dij，dij为加工路径中相邻两点的直线距离。i，j为路径中相邻两孔的孔号，i，j=1，2，…，n，且i≠j。G的一条巡回路线是经过图V中每个顶点恰好一次的单向路径，当遍历到最后一个点时数控刀具不需要返回到起点处，该条巡回路线不封闭，它不是一个回路。因此路径优化问题就在集合V中，采用遗传算法找到一个不重复的全排列V=｛V1，V2，…，Vn｝，使得整个路径的距离L最小，其目标函

采用数控钻削或铰削方式加工孔时，孔群中不同类型的孔需要通过切换不同加工刀具来完成。对于数控加工中心而言，所有刀具的更换都需要刀具重新回到机床参考点位置进行，因此要提高数控加工中心孔群的加工效率，只需考虑一种刀具情况下最短路径的优化。在上述前提下，数控孔群加工的过程可以描述如下：对某一类大小的孔，换上对应刀具后，刀具从机床参考点移动到孔群的某一个孔，沿着最短路径，从一个孔移动到下一个孔，直到该类孔都被加工完，刀具再返回到机床参考点处进行换刀。上述问题可以用如下数学优化模数优化数学模型可表述如式（1）：

2　改进遗传算法

遗传算法需要通过编码和各种遗传算子的作用来产生新的后代，在后代中以高概率地方式选择优良的种群作为遗传的种子，用以下一代的遗传操作。如果父代个体的竞争力高于子代个体，则父代作为良种继续遗传操作，而竞争力较弱的父代个体将被子代替代。如此反复进行，留下的优良子代即可作为问题的最优近似解。遗传算法在求解TSP问题中，编码、交叉和变异等方案非常关键，不同的编码、交叉和变异方案将有可能导致不同精度的解，有些不妥的方案甚至导致迭代过程中无法收敛，因此需要对上述方案进行特别处理。

2.1编码和交叉方案

以孔号作为染色体，采用自然数编码，这种编码意义明确，操作直接，但是随机产生后代和交叉后代过程中会遇到一定的问题，即求出的个体并非都是有效个体。为了避免出现错误的后代，需要对个体内染色体做一定的检验和处理，经检验和处理后的下一代个体必须满足如下三点：①随机产生的染色体首先必须是自然数；②各个染色体对应的自然数要属于顶点集合V=｛11，2，…，n ｝，其中n为孔的数量；③个体内的染色体互不相等。这种直接采用孔号为染色体的编码方案不仅简单而且不需要文献［1］中繁杂的编码和解码步骤，这将问题的求解变得更简单和更容易理解。

交叉算子是两个父代共同产生后代的一种方式，是优良父代把优良的基因遗传到子代中的一种方式。遗传算法中发展出了很多交叉算子，其中有部分映射交叉算子、循环交叉算子、基于序的交叉算子、序交叉算子和子巡回交换交叉算子等［10］。上述交叉算子对于一般优化问题的求解都有着很好的优点，能够实现优良基因的遗传，但是对于采用孔号为染色体的编码方案这些交叉算子将有一定的缺陷。不论按照上述哪种交叉算子，交叉算法都是在两个父代之间进行，这样就不可避免地会产生错误的遗传，从而导致遗传算法无法正常进行。因为以孔号为染色体的编码方案是不允许在同一个体内有相同的染色体，而按照上述的交叉算子都是不可避免地发生，因此需要对交叉算子做特别处理。具体的处理方法如下：①可先选定两个位置交叉，然后分别进行个体最优之间的交叉，产生的新个体如果存在染色体相同的情况则进行调整，采用的调整方法为用个体中未包括的染色体替代重复的染色体，具体实现方式如下：假设优良个体［1 5 4 7 3 2 6 8 10 9］与另一优良个体［3 5 6 1 3 2 8 6 10 9］在位置3和6的交叉，产生新一代的个体为［1 5 4 1 3 2 6 8 10 9］，显然新个体有重复的染色体，所以按照调整原则将相同染色体“1”其中的一个用未出现的染色体“4”来替代，则可以获得满足要求的新个体［7 5 4 1 3 2 6 8 10 9］。

2.2选择和变异方案

选择算子是解决父代中如何选择两个个体进行遗传操作的问题，也是如何为下一代挑选双亲的问题。由于父代个体的优良程度是不同的，按照生物进化论其基因在子代中的生存能力也是不同的，因此需要进行一定的选择操作使优良的基因能获得更大的机会遗传到下一代中去。遗传算法中有很多选择算子，比如随机均匀分布法、剩余法、均匀法、轮盘赌法和锦标赛法等［11］。遗传算法中判断个体优良与否的准则就是各自的适应度，这一操作是借用进化原则，即个体适应度越高，其被选择的机会就越多［12］。为此，采用与适应度值成正比的概率来进行选择，其具体操作是：首先，计算群体中所有个体适应度的总和∑fi；其次，计算每个个体的适应度所占的比例，第i个体所占比例为fi/∑fi，并以此作为每个个体遗传到下一代群体中的概率值。每个概率值为一个区域，全部概率之和为1；最后再产生一个0到1之间的随机数，由随机数出现在哪一个概率区来确定各个体被选中的次数。

变异是产生子代新个体的一种不可缺少的方式，变异的目的是为了防止丢失一些有用的遗传基因，尤其是当群体中的个体经遗传运算可能使某些串位失去多样性，从而可能失去有用的遗传基因，同时也可以克服局部最优解的弊端，变异运算是挖掘群体中个体的多样性。变异操作是按位进行的，以很小的概率随机地改变某一位或两位的值。虽然遗传算法有很多变异算子，但由于采用了孔号为染色体的遗传方案，因此变异不能采用通常的随机概率去改变个体的染色体，否则在个体内又会产生相同染色体的错误情形。为了解决上述可能发生的情况，须在遗传算法的程序内编写“不产生相同染色体”的约束条件，然后再采用“依赖约束条件”的变异算子进行计算。变异的具体实现方式如下：假设某一新代的个体［1 5 4 1 3 2 6 8 10 9］被选中要变异，则按照约束条件随机地选择两个染色体进行位置对调，比如第2和第6的位置实现对调变异，则可产生变异的新个体［1 2 4 1 3 5 6 8 10 9］。

3　计算实例与讨论

本文以文献［6］提供的孔群为研究对象，以表1的相关数据为计算依据，按照本文提出的改进遗传算法对表1中孔的编号和坐标点数据进行处理和计算。对孔群加工路径进行优化得到的目标就是使加工刀具在该零件上所有孔间的空行程移动路径最短。本文改进遗传算法的流程图如图1所示。改进遗传算法求解的最优加工路径是：17—20—18—22—14—5—7—2—4—9—3—6—16—21—23—15—13—12—8—11—1—19—10，按照这条优化加工路径数控刀具在加工中心上的最短空行程距离为291.968cm。文献［6］采用了粒子群算法和蚁群算法对表1中的孔群也进行了路径优化，表2是改进遗传算法、粒子群算法和蚁群算法三种智能算法的结果比较，从表2的比较结果可知，本文的最优数控加工路径是最短的，它更接近最优解。

表1　孔的坐标数据

表2　不同算法优化结果比较

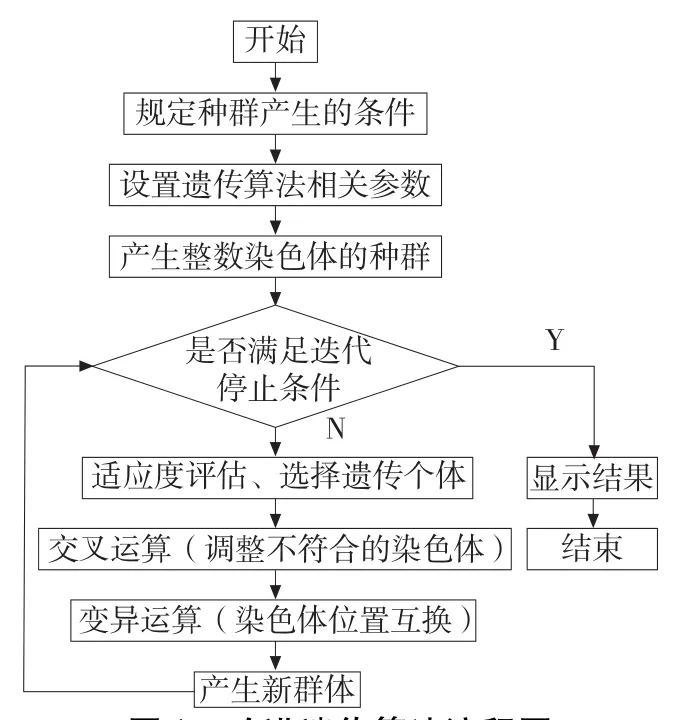
图1　改进遗传算法流程图

4　结束语

（1）针对孔群加工路径优化问题，提出了一种整数染色体的遗传算法。这种遗传算法以孔号为染色体，采用“优胜劣汰”的生物进化方法寻找问题最优近似解。这种采用孔号为染色体的编码方案不仅简单而且不需要繁杂的编码和解码步骤，简化了遗传算法的编程。

（2）遗传算法中的“交叉”和“变异”是产生新种群必要的步骤，为了避免在这些过程中产生不合格的个体，编制遗传算法程序时需要给定约束条件：产生的新个体不能包括重复的染色体，如果有重复的染色体则需要用未包括的染色体将其中一个替代。

（3）应用本文提出的改进遗传优化算法所获得的加工路径与参考文献［6］计算的结果进行对比检验，本文的计算结果具有更优的目标函数值，表明本文提出的改进遗传算法在处理孔群加工路径优化问题是有效的。

［1］许兆美，金卫凤，李健.基于遗传算法的孔群加工路径优化［J］.机械设计与制造，2011（2）：31-33.

［2］陈琳，刘晓琳，潘海鸿，等.孔群分类加工路径的优化算法［J］.制造业自动化，2013，35（17）：46-49.

［3］丁静，尚欣，周文玉.钣金件冲孔路径优化研究［J］.机床与液压，2006（3）：112-114

［4］曹宗华，吴斌，黄玉清，等.基于改进蚁群算法的多机器人任务分配［J］.组合机床与自动化加工技术，2013（2）：34-37.

［5］朱兴涛，张则强，胡俊逸.基于粒子群算法的U型装配线平衡问题研究［J］.组合机床与自动化加工技术，2012（4）：5-8.

［6］陈震，彭先涛.改进粒子群算法在紧固螺母路径中的优化［J］.制造业自动化，2013，35（17）：86-89.

［7］吴忻生，吴超成，刘海明.基于改进遗传算法的矩形件排样优化算法［J］.制造业自动化，2013，35（19）：55-58.

［8］冯剑，岳琪.模拟退火算法求解TSP问题［J］.森林工程，2008，24（1）：94-96.

［9］赵静，路银川，孔金生.基于量子遗传算法的多峰函数优化研究［J］.制造业自动化，2013，35（5）：94-96.

［10］张德丰.MATLAB实用数值分析［M］.北京：清华大学出版社，2012.

［11］马莉.MATLAB数学实验与建模［M］.北京：清华大学出版社，2010.

［12］赵俊书.优化技术与MATLAB优化工具箱［M］.北京：机械工业出版社，2011.

（编辑 赵蓉）

Optimization of NC Machining Path for Holes Based on Improved Genetic Algorithm

XIAO Jun-min
（Department of Mechanical and Electrical Engineering，Zhongshan Polytechnic，Zhongshan Guangdong 528404，China）

In order to shorten the vacant path of machining center tool and improve machining efficiency holes machining path needs to be optimized in the process of drilling and reaming.Holes machining path optimization of CNC machining center is a NP complete problem，so far there is not a very efficient algorithm to solve the optimal solution of NP problem.In order to solve the path optimization problem of holes machining a genetic algorithm of integer chromosome is proposed in the paper，and holes number is set as chromosome in the improved genetic algorithm.The genetic algorithm of integer chromosome can solve the approximate optimal solution based on the method of biological evolution.The solution example can show that the solution accuracy of improved genetic algorithm in the paper is higher than the solution accuracy of particle swarm algorithm and ant colony algorithm，so the improved genetic algorithm proposed in the paper can solve the path optimization problem of holes machining better.

genetic algorithm；holes machining；path optimization；CNC machining；NP problem

TH166；TG506

A

1001-2265（2015）02-0151-03 DOI：10.13462/j.cnki.mmtamt.2015.02.043

2014-06-04

广东省高等学校优秀青年教师培养计划资助项目（Yq2013195）

肖军民（1978—），男，江西峡江人，中山职业技术学院副教授，硕士，研究方向为先进制造技术，（E-mail）xiaojunmin517@163.com。