基于蒙特卡洛方法的数控磨床重要度分析*

范晋伟，王泽立，刘勇军，周中源，唐宇航，宋 毅

（北京工业大学机电学院，北京 100124）

基于蒙特卡洛方法的数控磨床重要度分析*

范晋伟，王泽立，刘勇军，周中源，唐宇航，宋 毅

（北京工业大学机电学院，北京 100124）

数控磨床系统复杂性高，各子系统之间关联性强。使用传统的重要度分析方法难以进行分析。在对数控磨床进行可靠性建模的基础上，获得整机及子系统的可靠度函数。通过评分方式获得各个子系统的关联度，并使用蒙特卡洛仿真方法对数控磨床各子系统进行重要度综合评价。此方法不仅考虑因素全面，而且在一定程度上减少了主观性的影响。使用此方法对某批数控磨床进行重要度综合评价结果表明该方法简便，有效，实用性强。

数控磨床；重要度；蒙特卡洛；子系统；可靠性建模

0　引言

数控磨床是一种精密加工设备，其可靠性好坏是评价数控磨床好坏的一项重要评价指标。为了提升整机的可靠性水平，需要有针对性的对各个子系统进行可靠性提升。子系统重要度是评判子系统重要程度的一个指标。子系统越重要，越应该优先提升该子系统的可靠性。因此，必须找到一种方法对系统进行更准确、更全面的重要度评价。

系统的重要度评定方法有很多。曾亮等［1］在1998年考虑了系统的多态性，提出了多状态单调关联系统元件重要度分析方法。孙红梅等［2］在2007年总结了基于故障树进行重要度分析的方法。2009年，李常有等［3］提出了基于改进的TOPSIS设备重要度分析法，此方法采用信息熵法求权重并应用TOPSIS方法得到重要度决策矩阵。姚成玉等［4］在2010年提出了基于模糊理论的T-S模糊故障树重要度分析方法。

以上文献中所述的方法虽然能够实现重要度评价，但都存在一定的缺陷。文献［2］没有考虑各个子系统的关联性。文献［3］对于重要度的评价主观性过强。文献［4］是基于故障树的重要度分析方法，没有建立完善的可靠性模型。

针对上述缺陷，本文提出一种利用历史故障数据对系统与子系统进行可靠性建模，并考虑子系统之间的关联性，同时运用蒙特卡洛仿真方法降低主观性的重要度评价方法。应用此方法对数控磨床进行重要度分析，来验证该方法的实用性。

1　子系统划分及可靠性建模

1.1子系统划分

一个复杂系统由于功能多，结构复杂。在进行分析时，需要将其划分为若干个子系统来降低复杂性。假设系统Ω，对其进行子系统划分，其子系统集为Ri，Ri=（子系统1，子系统2，…，子系统n）。

1.2可靠性建模

对系统进行可靠性建模，要找到可能符合的分布模型，再利用适当的拟合方法对其进行参数估计。最后验证可靠性模型的有效性。

由文献［5］知，数控磨床可靠性模型符合指数分布或威布尔分布。

1.2.1指数分布可靠性建模

指数分布的分布函数为：

整理为：

对式两边取对数：

可化为一元线性关系式：

由文献［5］知：F（t）可由中位秩估计F（ti）代替，中位秩估计表达式为：

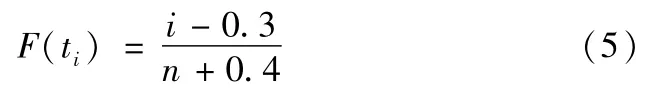
使用最小二乘法进行参数估计，求得最小二乘参数为：

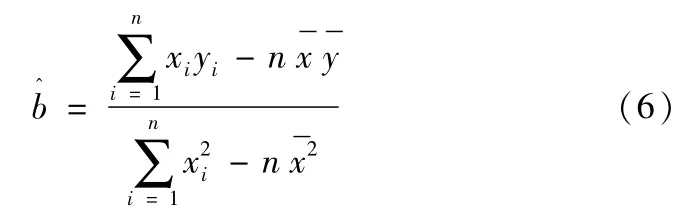
其中

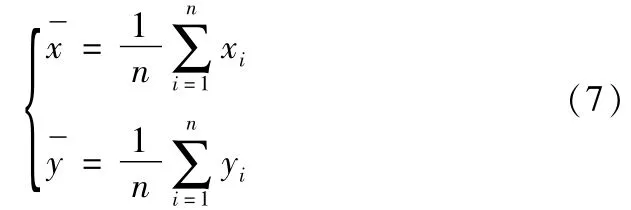
求得指数分布参数

得到可靠度函数：

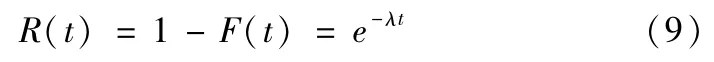
1.2.2威布尔分布可靠性建模

两参数威布尔分布的分布函数为：

整理为：

对式取两次对数：

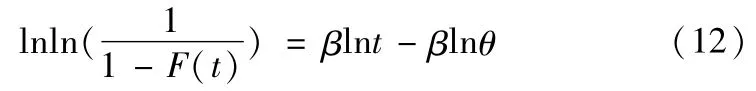
可化为一元线性关系式：

F（t）也由中位秩估计F（ti）代替。使用最小二乘法进行参数估计，求得最小二乘参数为：

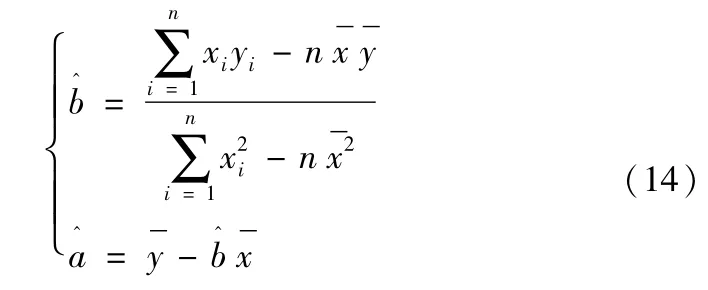
其中

求得威布尔参数：

得到可靠度函数：

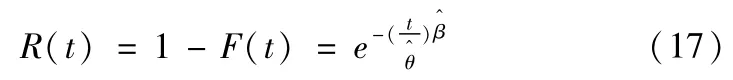
1.2.3可靠性分布拟合优度检验及模型优选

K-S检验法是对计算样本数据的观察值与拟合模型计算值求差。如果差小于允许值时，接受拟合模型；反之，不接受。

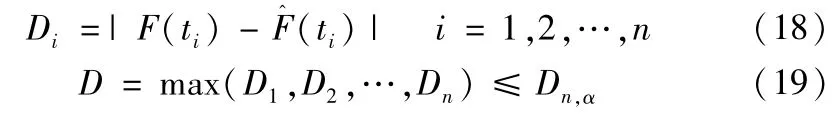
Di——观察值与拟合模型计算值的差

Dn，α——观察值与拟合模型计算值的差临界值，可通过查表获得。

采用相关指数法［7］来进行模型优选。

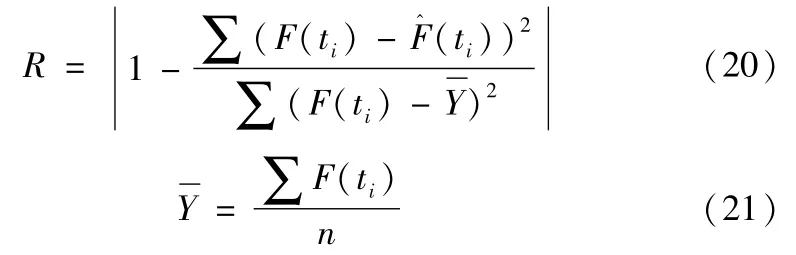
如果指数分布的相关指数R指数大于威布尔分布的相关指数R威布尔，则选取指数分布为可靠性模型的优选分布模型；反之，则选取威布尔分布为可靠性模型的优选分布模型。

2　临界重要度指标

根据文献［2］，将临界重要度重新定义为以下形式：

Rsys（t）——整机可靠度函数；

Ri（t）——子系统可靠度函数。

临界重要度既考虑了整机系统可靠度随子系统可靠度变化的变化率，又考虑了子系统本身可靠度大小的程度。如果整机系统可靠度因某一子系统可靠度变化而变化的变化率比较大，说明提高这一子系统的可靠度会使整机可靠度得到更大的提升。如果子系统的可靠度越低，说明能够提升的潜力就越大。从这两方面综合考虑，能够更全面的评价子系统的重要度。

将各子系统的临界重要度写成向量形式：

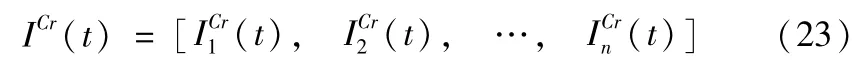
3　子系统关联度

各个子系统相互联系，相互作用，共同影响整个系统的状态。采用专家评价的方式来得到子系统的关联度。子系统评分取值区间在0～1之间，越靠近0表示影响越微小，越靠近1表示影响越严重。

得到评分值后，建立与之对应的子系统关联度矩阵。

子系统关联度矩阵：

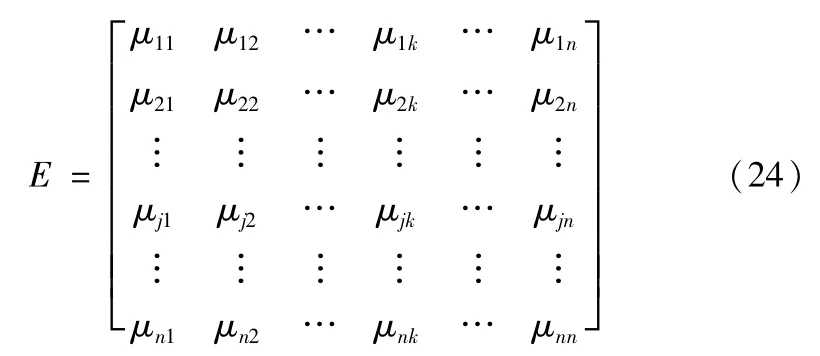
式中：μjk表示子系统j出故障后对子系统k的影响评分值。可知，μii=0。子系统的关联度定义如下：

得到子系统关联度向量：

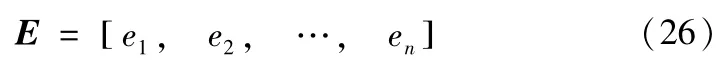
式中ej表示子系统j的关联度。ej越大，说明子系统j对其它子系统的影响越大。

4　基于蒙特卡洛方法的重要度评价

定义新的重要度评价指标为：

写成向量形式为：

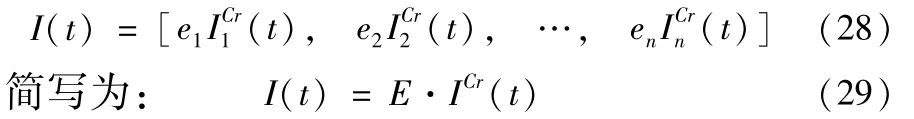
ICr（t）是时间t的函数，每个时间t都对应一组子系统重要度，以一个时间点所对应的重要度来评价子系统的重要度是不全面的；同时，为了减少子系统关联度评分的主观性。采用蒙特卡洛模拟方法，使用Matlab软件进行数值计算，获得T=［0，t］区间上的综合重要度。具体方法是设定步长Δt，每隔步长取一组数据，并且按关联度评分排序随机分配关联度评分值，由式（27）计算出一个时间点所对应的重要度。对T=［0，t］区间上所有的重要度求和，得到累积重要度。最后对累积重要度进行归一化，最终得到T=［0，t］区间上各个子系统的重要度。

5　应用实例

以北京第二机床厂某批9台数控磨床为例进行综合重要度评价。对数控磨床进行子系统划分，并按照上述方法进行可靠性建模，结果见表1。

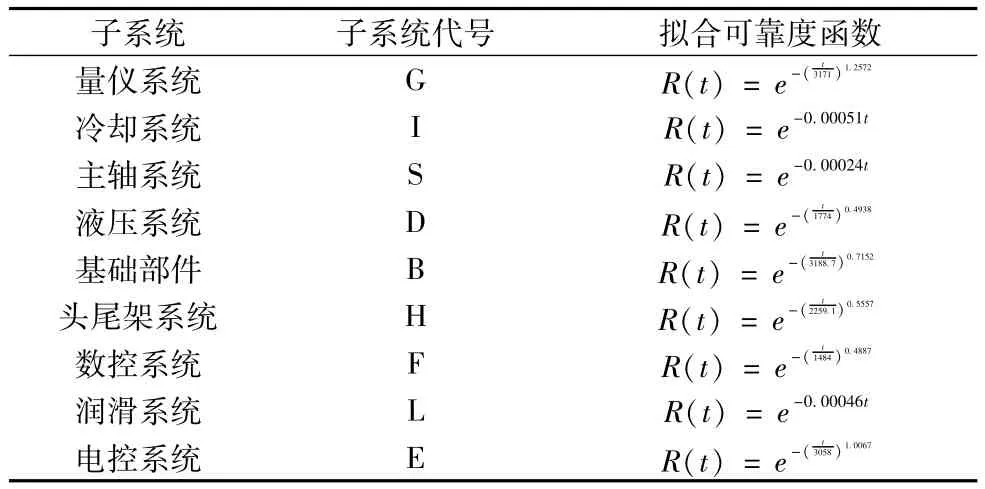
表1　子系统代号和可靠度函数表

整机的拟合可靠度为：

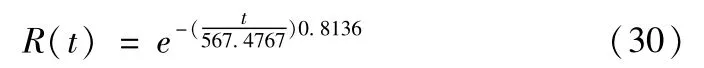
数控磨床的任何一个子系统出现故障都会导致整机故障。因此，数控磨床系统是典型的串联系统。可知：

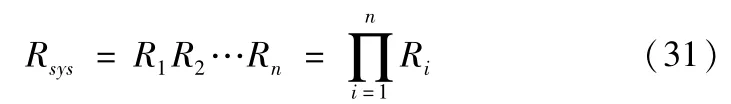
临界重要度表达式为：

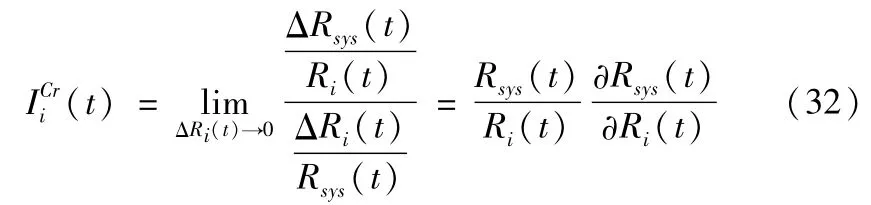
将式（31）带入式（32）中可得：

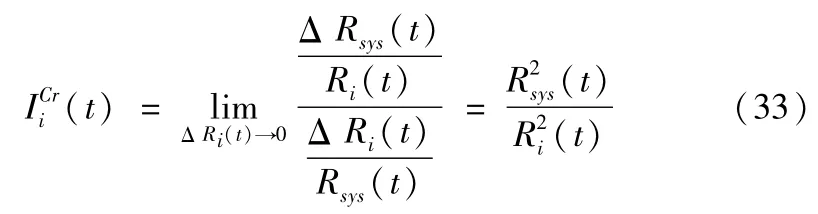
由式（33）计算出各个子系统的临界重要度表达式。子系统的临界重要度表达式为：

对子系统进行关联度打分，结果见表2。

表2　子系统关联度打分表

通过表2数据，获得子系统关联度矩阵：

由式（25）计算得到子系统关联度向量：

从结果可以得到子系统关联度大小的排序：电控系统＞数控系统＞液压系统＞主轴系统＞基础部件＞头（尾）架系统＞量仪系统＞冷却系统＞润滑系统。

基于蒙特卡洛方法，使用Matlab软件进行蒙特卡洛仿真模拟，仿真的循环次数N=150。

程序流程图如图1所示。

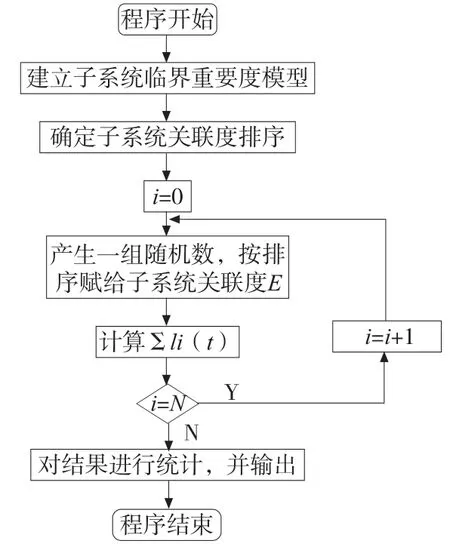
图1　蒙特卡洛程序流程图

每次循环产生一组随机数，将随机数按大小顺序赋给对应的子系统作为关联度，进而按照式（28）计算出综合重要度，对其进行累加，得到累积重要度。对累积重要度进行数据拟合，拟合曲线如图2所示。

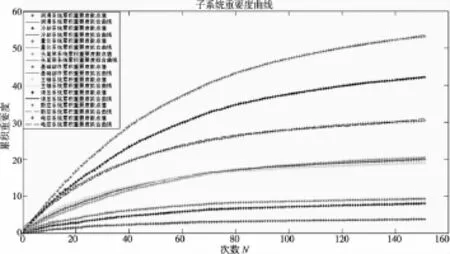
图2　子系统累积重要度拟合曲线

累积重要度的三次多项式拟合表达式及其导数列于表3中。

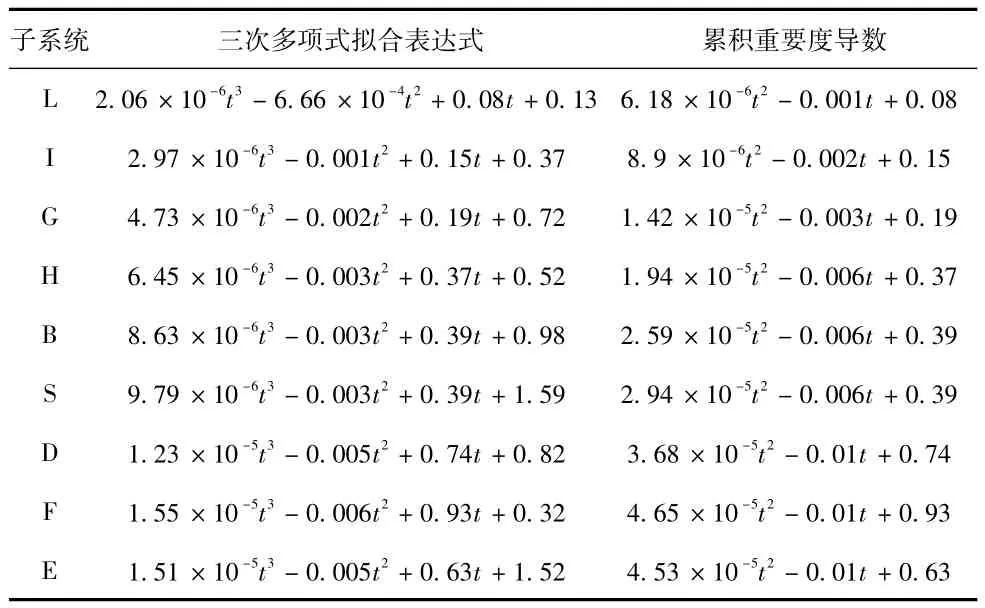
表3　累积重要度拟合多项式及其导数

当t=10，根据表3，计算出累积重要度的导数，即增长率G：GL=0.06，GI=0.11，GG=0.14，GH= 0.26，GB=0.28，GS=0.281，GD=0.56，GF=0.75，GE=0.45。可以看出，数控系统的累积重要度增长率最大为0.75；润滑系统累积重要度增长率最小为0.06，两个系统累积重要度增长率相差12.5倍。从图2中可以看出，头（尾）架系统、基础部件和主轴系统这三个子系统的累积重要度很接近。在第50次累加之前，三者累积重要度的排序为：主轴系统＞基础部件＞头（尾）架系统。在循环结束时，三者累积重要度的排序为：头（尾）架系统＞基础部件＞主轴系统。

累积重要度进行归一化后的结果为：

将归一化后的累积重要度作为评价数控磨床各个子系统重要度的指标。

最后，得到的子系统重要度的先后排序为：数控系统＞液压系统＞电控系统＞头（尾）架系统＞基础部件＞主轴系统＞量仪系统＞冷却系统＞润滑系统。

数控系统、液压系统和电控系统重要度排在前三位。其中电控系统的电子元器件较多，故障频发，关联度排在第一；数控系统时常出现数控指令不能正常运行的情况，关联度排在第二；液压系统出现堵塞和泄漏的情况比较多，关联度较高。可见，关联度较高是导致这三个子系统重要度较高的原因。在对数控磨床进行可靠性提升时，考虑到这三个子系统的重要度较高，应视为重点子系统优先进行可靠性优化。

头（尾）架系统、基础部件和主轴系统重要度排在4到6位，但差距不大。在对数控磨床进行可靠性提升时，应综合考虑其他因素来确定需要优先提升的子系统。量仪系统、冷却系统和润滑系统重要度较低，不作为优先提升可靠性的子系统。

6　总结

本方法考虑了各个子系统之间的关联度，并弱化了评价的主观影响，简单易行，易于通过编程实现计算。通过实例证明该方法可以有效的对数控磨床系统进行了子系统的重要度评价，为制定数控磨床可靠性提升的决策路线提供了依据，能够更加有针对性的对各个子系统进行可靠性改进，进而更有效的提升整机可靠性。事实证明，该方法对数控磨床可靠性提升有着十分重要的指导意义。

［1］曾亮，郭欣.多状态单调关联系统元件重要度分析［J］.系统工程与电子技术，1998（2）：72-74.

［2］孙红梅，高齐圣，朴营国.关于故障树分析中几种典型重要度的研究［J］.电子产品可靠性与环境试验，2007，25（2）：39-42.

［3］李常有，徐敏强.基于改进的TOPSIS的设备重要度分析［J］.振动与冲击，2009，28（6）：164-167.［4］姚成玉，张荧驿，王旭峰，等.T-S模糊故障树重要度分析方法［J］.中国机械工程，2011，22（11）：1261-1268.

［5］贾敬阳.数控砂带磨床可靠性评估与故障分析［D］.吉林：吉林大学，2013.

［6］卢世荣，方逵，周经纶.BDD表示下的部件重要度的计算［J］.系统工程与电子技术，1999，21（3）：69-72.

［7］高雪莉，催利荣.单元重要度在可靠性工程中的应用［J］.技术基础研究与应用，2005（12）：1-4.

［8］Beeson S，D Andrews J.Importance Measures for Non-Coherent-System Analysis［J］.IEEE TRANSACTIONS ON RELIABILITY，2003，52（3）：301-310.

［9］Shu-bin SI，Li-li ZHANG，Zhi-qiang CAI，et al.Integrated Importance Measure of Binary Coherent Systems［C］.Xiamen：IEEE 17Th International Conference on Industrial Engineering and Engineering Management（IE&EM），2010：932-936.

［10］Xi-Zhao WANG，Jun-Hai ZHAI，Su-Fang ZHANG.Fuzzy Decision Tree Based On The Important Degree Of Fuzzy Attribute［C］.Kunming：Machine Learning and Cybernetics，2008 International Conference on，2008：511-516.

［11］Chen J，BiW.Joint Failure-Importance of Components in Fault Tree［C］.Changsha：International Conference on Measuring Technology and Mechatronics Automation，2010：537-540.

［12］Lu L，Jiang J.Joint Failure Importance for Noncoherent Fault Trees［J］.IEEE TRANSACTIONS ON RELIABILITY，2007，56（3）：435-443.

（编辑 赵蓉）

The Importance Analysis of CNC Grinding Machine Based on Monte Carlo Method

FAN Jin-wei，WANG Ze-li，LIU Yong-jun，ZHOU Zhong-yuan，TANG Yu-hang，SONG Yi
（Mechanical and Electrical Engineering College，Beijing University of Technology，Beijing 100124，China）

CNC grinding system complexity is high，with the strong correlation between the subsystems.U-sing the traditional importance analysis method is difficult to analyze.With CNC grinding machine reliability modeling，get the subsystem reliability function.By grading correlation of each subsystem，and using Monte Carlo simulation method to evaluate the important degree of each subsystem of CNC grinding machine comprehensively.This method not only considered factors comprehensively，but reduce the influence of subjectivity in a certain extent.Using this method to evaluate the important degree of a batch of CNC grinding machine，the evaluation results show that the method is simple，effective and practical.

CNC grinding machine；important degree；Monte Carlo；subsystem；reliability modeling

TH165；TG65

A

1001-2265（2015）02-0074-04 DOI：10.13462/j.cnki.mmtamt.2015.02.021

2014-04-14

国家科技重大专项：中高档国产数控磨床可靠性规模化提升工程（2013ZX04013047）；国家自然科学基金资助项目（51275014）

范晋伟（1965—），男，河南西平人，北京工业大学教授，博士生导师，主要从事数控技术、精密加工、伺服控制方面研究，（E-mail）wangzeli512@163.com。