基于修正自适应匹配滤波器的机动目标检测方法

李　海　刘新龙　周　盟　刘维建

①（中国民航大学天津市智能信号与图像处理重点实验室　天津　300300）

②（空军预警学院黄陂士官学校　武汉　430019）

基于修正自适应匹配滤波器的机动目标检测方法

李海*①刘新龙①周盟①刘维建②

①（中国民航大学天津市智能信号与图像处理重点实验室天津300300）

②（空军预警学院黄陂士官学校武汉430019）

机动目标回波的多普勒走动和训练样本不足导致常规自适应匹配滤波器（Adaptive Matched Filter，AMF）检测机动目标时运算量大且性能不佳。针对此问题，该文提出一种基于修正AMF的机动目标检测方法。该方法首先通过对角加载减少样本空间自由度，从而降低对训练样本数的需求；然后以3次相位变换（Cubic Phase Transform，CPT）分离估计加速度，并以估计值补偿多普勒走动，降低联合匹配搜索维度，进而减少运算量；最后进行积累检测。仿真结果表明，该方法运算量低，可实现小样本下机动目标的有效检测，具有恒虚警（Constant False Alarm Rate，CFAR）特性。

机动目标检测；自适应匹配滤波器；3次相位变换；对角加载；多普勒走动

1　引言

空时自适应处理［1-3］（Space-Time Adaptive Processing，STAP）是机载相控阵雷达杂波抑制的有效技术，以空时联合为框架实现目标检测的自适应处理称为空时自适应检测处理 （Space-Time Adaptive Detection，STAD）［4］，STAD同时进行杂波抑制与目标检测，通常具有恒虚警（Constant False Alarm Rate，CFAR）特性。其中广义似然比检测器（Generalized Likelihood Ratio，GLRT）［5］、自适应匹配滤波器（Adaptive Matched Filter，AMF）［6，7］和自适应相干估计器（Adaptive Coherence Estimation，ACE）［8］是3种著名的多通道STAD检测器，可实现对匀速运动目标的有效检测。然而，随着航空技术的发展，空中目标的机动性越来越好，即目标通常具有加速度［9］，使得常规STAD检测器不能直接用于机动目标检测。近年来，机动目标的检测在军事和民用领域受到了广泛关注［10-13］，尤其在军事领域，来袭目标往往通过机动飞行进行军事打击，对国防体系构成严重威胁，如何及时有效地实现对机动目标的检测和预警是未来雷达监视系统的一大挑战［11，12］。因此，研究STAD检测器对机动目标的有效检测具有重要的意义。

本文考虑AMF对机动目标的检测问题。对于具有径向加速度的机动目标，其回波信号具有多普勒走动［9］，则常规AMF检测器对机动目标检测时，需要进行包括多普勒1次项和多普勒2次项的匹配搜索，运算复杂度高。与此同时，AMF的检测性能与用于估计杂波协方差矩阵的独立同分布（Independent and Identically Distributed，IID）训练样本数有关［7］。文献［14］指出，为使信杂噪比损失（Signal to Clutter plus Noise Ratio Loss，SCNR Loss）［3］小于3 dB，IID训练样本数L应大于两倍的系统维数N，即。然而现代相控阵雷达常具有成百上千的接收阵元［15］，系统维数通常比较高；且机载雷达所面临的实际环境比较复杂，杂波往往具有非均匀特性［16］；尤其在机载非正侧视阵雷达中，杂波具有距离依赖性［17］，足够多的IID训练样本很难满足，导致检测性能不佳。因此，常规AMF检测器直接用于机动目标检测时存在运算量高以及检测性能不佳的问题，难于实际应用。

针对上述问题，本文提出一种基于修正AMF的机动目标检测方法，该方法首先采用对角加载（Diagonal Loading，DL）技术［18，19］减少样本空间的自由度个数（Number of Degrees of Freedom，NDoF）［20］，降低检测器对IID训练样本数的需求；为了减少运算量，文中通过3次相位变换（Cubic Phase Transform，CPT）［21］对机动目标加速度分离估计，以加速度估计值补偿机动目标回波的多普勒走动项之后进行积累检测，即降低了匹配搜索的维度。最后，仿真结果验证了该方法的有效性。

2　问题描述

那么，常规AMF做机动目标检测时，需进行包括多普勒1次项以及多普勒2次项的匹配搜索，运算复杂度高。

与此同时，AMF的目标检测包括杂波抑制过程，其检测性能与用于估计杂波协方差矩阵R的IID训练样本数有关［7］；为使SCNR Loss小于3 dB，训练样本数L应大于两倍的系统维数［14］，此时协方差矩阵估计值为：

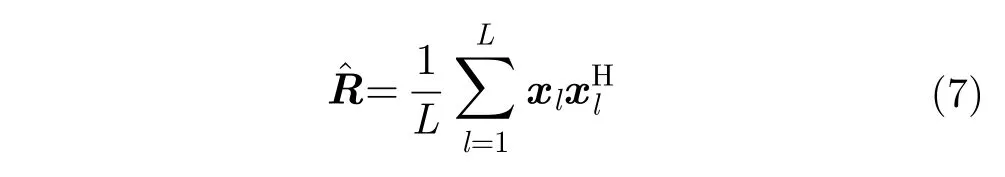
综上所述，常规AMF用于机动目标检测时需进行联合匹配搜索，运算量高；同时，实际中足够多的训练样本很难满足，导致AMF检测性能不佳。本文考虑AMF对机动目标的检测问题，分别从降低运算量以及实现小样本下机动目标检测两个方面讨论。

3　本文算法

针对常规AMF用于机动目标检测存在运算量大以及检测性能不佳的问题，本文采用分离估计机动目标加速，降低匹配搜索维度的方法减少运算量；通过对角加载技术减少样本空间自由度个数，降低检测器对训练样本数的需求，进而实现AMF在小样本下的机动目标检测。以下分别从多普勒走动补偿和对角加载AMF检测（DL-AMF）两个方面展开论述。

3.1多普勒走动补偿

本文通过CPT［21］分离估计机动目标加速度，然后以加速度估计值补偿多普勒走动项。设机动目标基带回波信号为s（k），不考虑角度信息，则可表示为：

式中M和N分别表示多普勒和角度通道个数。

3.3算法流程图

本文所提算法流程如图1所示，具体步骤包括：

步骤2对待测单元数据进行杂波抑制［3］，并通过CPT分离估计机动目标加速度；

步骤4对多普勒走动项补偿后的数据进行DLAMF检测。

图1　算法流程图Fig. 1　Flow diagram of algorithm

4　仿真分析

为验证本文所提方法的有效性，以下分别从加速度估计、多普勒走动补偿以及目标检测几个方面进行仿真分析。

4.1加速度估计和多普勒走动补偿仿真与分析

本节仿真参数如表1所示。

仿真中加速度估计的均方根误差（Root Mean Square Error，RMSE）定义为：

表1　系统与仿真参数Tab. 1　Parameters of system and simulation

不同信噪比（Signal to Noise Ratio，SNR）下，RMSEa随样本数的变化情况如图2所示。可以看出：RMSEa随样本数的增加而减小，当样本数大于2倍杂波大特征值个数时，RMSEa趋于稳定，说明加速度的估计相对于样本个数具有稳健性；同时，在确定样本数的情况下，当SNR增大时，RMSEa减小，说明加速度估计性能随SNR增大而得到改善，即加速度估计性能随SNR具有收敛性。

图2　RMSEa随样本数变化曲线Fig. 2　RMSEaversus number of training sample

图3　CAG随加速度估计误差变化曲线Fig. 3　CAG versus estimated error of acceleration

4.2检测性能仿真与分析

本部分仿真参数如表2所示，其中系统参数与表1一致。

为了进一步比较本文方法与常规AMF所需样本数的比较，图5给出了SCNR Loss随样本数的变换曲线。可以看出在SCNR Loss为-3 dB时，相比于常规AMF，本文方法所需训练样本数少，这是因为本文采用了DL技术，减少了样本空间NDoF，进而降低了对训练样本数的需求。这里需指出的是，在训练样本数小于系统维数时（），协方差矩阵估计值为奇异矩阵，故图5中没有给出时常规AMF SCNR Loss变化曲线。

图4　L=2p和L=2N时检测性能比较Fig. 4　PD comparison when L=2p and L=2N

图6　不同样本数时检测性能比较Fig. 6　PD comparison under different number of training sample

4.3计算量比较

表2　仿真参数Tab. 2　Parameters of simulation

图5　信杂噪比损失比较Fig. 5　Comparison of SCNR loss

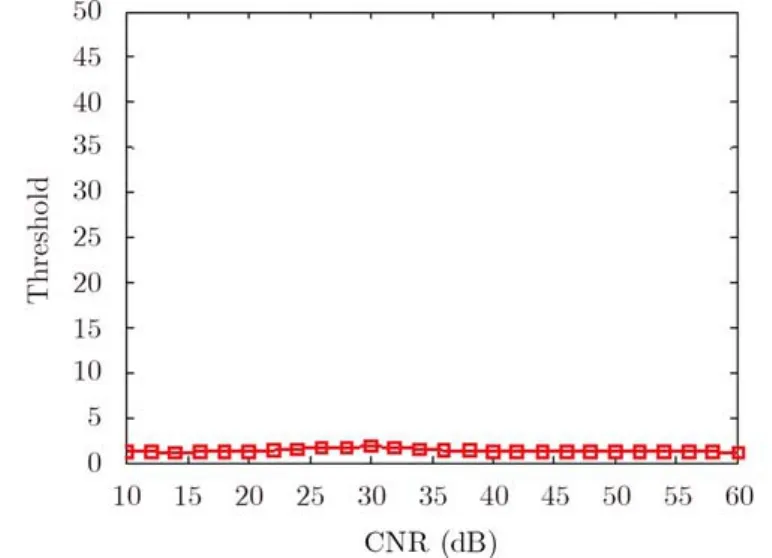
图7　检测门限随CNR变化曲线Fig. 7　Thresholds of the detector versus CNR

本部分记1次复乘为1次运算，表3中比较了本文方法与常规AMF方法的运算量。表中和分别表示加速度和速度搜索区间，和分别为加速度和速度搜索步长；表示常规AMF方法所需训练样本个数，为本文方法所需样本数，其中表示杂波大特征值个数；实例运算量是指在表2仿真参数下的运算量。

由表3可以看出，本文方法的运算量低于常规AMF方法的运算量。

表3　运算量比较Tab. 3　Comparison of calculation

5　结论

本文提出一种基于修正自适应匹配滤波器的机动目标检测方法，该方法通过对角加载技术降低检测器对训练样本数的需求；以CPT分离估计机动目标加速度，并以估计值补偿目标信号的多普勒走动项，降低了联合匹配搜索维度；该方法加速度估计性能具有稳健性，可实现多普勒走动的有效补偿，进而可实现有效的积累检测。实验结果表明，本文方法计算量低，可实现在小样本下机动目标的有效检测，且具有CFAR特性。

［1］Klemm R. Principles of Space-time Adaptive Processing［M］. London: The Institution of Electrical Engineers，2002: 87-100.

［2］Melvin W L. A STAP overview［J］. IEEE Aerospace and Electronic Systems Magazine，2004，19（1）: 19-35.

［3］Ward J. Space-time adaptive processing for airborne radar［R］. Technical Report 1015，MIT Lincoln Laboratory，1994: 1-79.

［4］王永良，刘维建，谢文冲，等. 机载雷达空时自适应检测方法研究进展［J］. 雷达学报，2014，3（2）: 201-207. Wang Y L，Liu W J，Xie W C，et al.. Research progress of space-time adaptive detection for airborne radar［J］. Journal of Radars，2014，3（2）: 201-207.

［5］Kelly E J. An adaptive detection algorithm［J］. IEEE Transactions on Aerospace and Electronic Systems，1986，22（1）: 115-127.

［6］Chen W S and Reed I S. A new CFAR detection test for radar［J］. Digital Signal Processing，1991，1（4）: 198-214.

［7］Robey F C，Fuhrmann D R，Kelly E J，et al.. A CFAR adaptive matched filter detector［J］. IEEE Transactions on Aerospace and Electronic Systems，1992，28（1）: 208-216.

［8］Kraut S and Scharf L L. The CFAR adaptive subspace detector is a scale-invariant GLRT［J］. IEEE Transactions on Signal Processing，1999，47（9）: 2538-2541.

［9］Li X L，Cui G L，Yi W，et al.. Coherent integration for maneuvering target detection based on Radon-Lv's distribution［J］. IEEE Signal Processing Letters，2015，22（9）: 1467-1471.

［10］Ru J F，Jilkov V P，Li X R，et al.. Detection of target maneuver onset［J］. IEEE Transactions on Aerospace and Electronic Systems，2009，45（2）: 536-554.

［11］Zhu S Q，Liao G S，Yang D，et al.. A new method for radar high-speed maneuvering weak target detection and imaging［J］. IEEE Geoscience and Remote Sensing Letters，2014，11（7）: 1175-1179.

［12］Chen X L，Huang Y，Liu N B，et al.. Radon-fractional ambiguity function-based detection method of lowobservable maneuvering target［J］. IEEE Transactions on Aerospace and Electronic Systems，2015，51（2）: 815-833.

［13］Winters D W. Target motion and high range resolution profile generation［J］. IEEE Transactions on Aerospace and Electronic Systems，2012，48（3）: 2140-2153.

［14］Reed I S，Mallett J D，and Brennan L E. Rapid convergence rate in adaptive arrays［J］. IEEE Transactions on Aerospace and Electronic Systems，1974，10（6）: 853-863.

［15］Güvensen G M，Candan C，Orguner U，et al.. On generalized eigenvector space for target detection in reduced dimensions［C］. Proceedings of the IEEE International Radar Conference，Arlington VA，USA，2015: 1316-1321.

［16］Melvin W L. Space-time adaptive radar performance in heterogeneous clutter［J］. IEEE Transactions on Aerospace and Electronic Systems，2000，36（2）: 621-633.

［17］同亚龙，王彤，文才，等. 一种稳健的机载非正侧视阵雷达杂波抑制方法［J］. 电子与信息学报，2015，37（5）: 1044-1050.

Tong Y L，Wang T，Wen C，et al.. A robust clutter suppression method for airborne non-sidelooking radar［J］. Journal of Electronics & Information Technology，2015，37（5）: 1044-1050.

［18］Carlson B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays［J］. IEEE Transactions on Aerospace and Electronic Systems，1988，24（4）: 397-401.

［19］Guerci J R and Bergin J S. Principal components，covariance matrix tapers，and the subspace leakage problem［J］. IEEE Transactions on Aerospace andElectronic Systems，2002，38（1）: 152-162.

［20］Wu Y，Tang J，and Peng Y N. On the essence of knowledge-aided clutter covariance estimate and its convergence［J］. IEEE Transactions on Aerospace and Electronic Systems，2011，47（1）: 569-585.

［21］O'shea P. A fast algorithm for estimating the parameters of a quadratic FM signal［J］. IEEE Transactions on Signal Processing，2004，52（2）: 385-393.

［22］Reed I S，Gau Y L，and Truong T K. CFAR detection and estimation for STAP radar［J］. IEEE Transactions on Aerospace and Electronic Systems，1998，34（3）: 722-735.

［23］Mestre X. Improved estimation of eigenvalues and eigenvectors of covariance matrices using their sample estimations［J］. IEEE Transactions on Information Theory，2008，54（11）: 5113-5129.

［24］Wang Y L，Liu W J，Xie W C，et al.. Reduced-rank spacetime adaptive detection for airborne radar［J］. Science China Information Sciences，2014，57: 082310.

［25］Guerci J R. Space-time Adaptive Processing for Radar［M］. London: Artech House，2003: 51-72.

［26］Benaych Georges F and Nadakuditi R R. The eigenvalues and eigenvectors of finite，low rank perturbations of large random matrices［J］. Advances in Mathematics，2011，227（1）: 494-521.

［27］Hiemstra J D. Robust implementations of the multistage wiener filter［D］. ［Ph.D. dissertation］，Virginia Polytechnic Institute and State University，2003.

［28］Skolnik M I. Radar Handbook［M］. New York: McGraw-Hill，1990.

［29］Gerlach K and Picciolo M L. Airborne/spacebased radar STAP using a structured covariance matrix［J］. IEEE Transactions on Aerospace and Electronic Systems，2003，39（1）: 269-281.

［30］刘维建，谢文冲，王永良. 基于对角加载的自适应匹配滤波器和自适应相干估计器［J］. 系统工程与电子技术，2013，35（3）: 463-468.

Liu W J，Xie W C，and Wang Y L. AMF and ACE detectors based on diagonal loading［J］. Systems Engineering and Electronics，2013，35（3）: 463-468.

［31］Gau Y L. CFAR detection algorithm for STAP airborne radar［D］. ［Ph.D. dissertation］，University of Southern California，1996.

李海（1976-），男，天津人，现为中国民航大学副教授，研究方向为空时自适应信号处理、机载气象雷达信号处理等。

E-mail: haili@cauc.edu.cn

刘新龙（1984-），男，甘肃张掖人，现为中国民航大学硕士研究生，研究方向为空时自适应信号处理、动目标检测。

E-mail: xinl_liu@qq.com

周盟（1988-），男，四川广汉人，现为中国民航大学硕士研究生，研究方向为空时自适应信号处理、动目标检测、机载气象雷达信号处理。

E-mail: bard_belief@hotmail.com

刘维建（1982-），男，山东莱芜人，现为空军预警学院黄陂士官学校助教，主要研究方向为雷达信号处理、多通道信号检测、阵列信号处理和统计信号处理。

E-mail: liuvjian@163.com

Detection of Maneuvering Target Based on Modified AMF

Li Hai①Liu Xin-long①Zhou Meng①Liu Wei-jian②

①（Tianjin Key Laboratory for Advanced Signal Processing，Civil Aviation University of China，Tianjin 300300，China）
②（Huangpi NCO School of Air Force Early Warning Academy，Wuhan 430019，China）

Owing to the Doppler frequency migration of the return signal of maneuvering targets and finite training samples，it is difficult to detect maneuvering targets by conventional Adaptive Matched Filter （AMF）detectors. To solve this problem，a new method is proposed. First，to minimize sample size impairments，the diagonal loading technique was adopted to decrease the degrees of freedom of the sample space. Second，the Doppler frequency migration was compensated by the estimated acceleration which was estimated by the cubic phase transform，so as to reduce the dimension of matched searching and degrade the heavy calculation load. Finally，accumulation detection was conducted. The simulation results suggest that the proposed method can efficiently detect maneuvering target in finite sample situations with simple computation and constant false alarm rate detection.

Maneuvering target detection； Adaptive matched filter； Cubic phase transform； Diagonal loading；Doppler frequency migration

s: The National Natural Science Foundation of China （61471365，61231017，61571442），National University's Basic Research Foundation of China （3122015B002），Foundation for Sky Young Scholars of Civil Aviation University of China

TN957

A

2095-283X（2015）-05-0552-08 DOI：10.12000/JR15105

李海，刘新龙，周盟，等. 基于修正自适应匹配滤波器的机动目标检测方法［J］. 雷达学报，2015，4（5）: 552-559.

10.12000/JR15105.

Reference format：Li Hai，Liu Xin-long，Zhou Meng，et al.. Detection of maneuvering target based on modified AMF［J］. Journal of Radars，2015，4（5）: 552-559. DOI: 10.12000/JR15105.

2015-09-18； 改回日期：2015-10-25

李海haili@cauc.edu.cn

国家自然科学基金（61471365，61231017，61571442），中央高校基本科研业务费项目（3122015B002），中国民航大学蓝天青年学者培养经费