基于联系数正态模糊数型多属性群的决策方法

顾翠伶

（周口师范学院 数学与统计学院，河南 周口 466000）

基于联系数正态模糊数型多属性群的决策方法

顾翠伶

（周口师范学院 数学与统计学院，河南 周口 466000）

针对决策属性值、专家权重、属性权重均为正态模糊数型的模糊多属性决策问题给出一种解决方案。依据正态模糊数的期望与方差，提出一种分值函数，并以此把正态模糊型的专家权重转化为精确权重。将以正态模糊数给出的各个专家的属性值及各个属性权重转化为联系数，然后按照联系数的运算求解模糊多属性决策问题，实例验证新方法的可行性和有效性。

正态模糊数；联系数；模糊多属性决

多属性群决策问题的理论与方法已经成为决策科学、系统科学和管理科学等领域研究的重要内容，它广泛应用于社会、经济、管理等多个领域。近年来，关于三角模糊数、梯形模糊数、直觉模糊数型的多属性决策已经有了广泛研究。但三角模糊数和梯形模糊数的隶属函数是线性隶属函数形态，在亦此亦彼性的刻画上虽然连续，但出现突变点，这种突变不符合中介过渡性质的渐变特征。但是正态模糊数在多属性决策中的应用还不多。桑广提出基于相似度与规范化理想解的决策方法。本文针对属性值、属性权重与专家权重都用正态模糊数表示的多属性决策问题，建立联系数决策模型，并给出决策步骤，实例验证本文方法的有效性。

1　预备知识

1.1正态模糊数

定义1：若模糊数Ã的隶属函数为

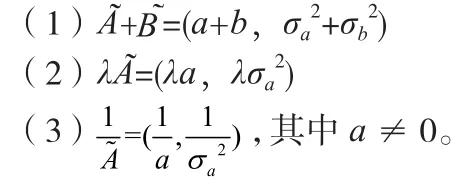
定义2：模糊数Ã的期望为

定义3：模糊数Ã的方差为

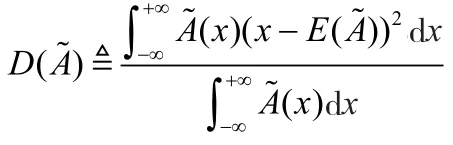
1.2联系数

定义5：设A、B为非负实数，i∈［-1，1］，则称A+Bi是联系数，简称联系数。

根据集对分析，联系数A+Bi中的A称为联系数的同部，是相对确定的；Bi称为联系数的异部，具有不确定性，i为不确定数。一般用μ表示，记为μ=A+Bi。

联系数的运算法则：

（1）加法运算：μ1=A1+B1i，μ2=A2+B2i，则μ=μ1+μ2=（A1+A2）+（B1+B1）i。

（2）乘法运算：μ1=A1+B1i，μ2=A2+B2i，则：

μ=μ1μ2=A1A2+（A1B2+A2B1+B1B2）i特别地有：（A+Bi）2=A2+（2AB+B2）i。

1.3正态模糊数转化为联系数

设正态模糊数为Ã=（a，σ2），令A=a，B=σ，则A+Bi=a+σi为正态模糊数向联系数的转化公式。

2　基于联系数的正态模糊数型多属性决策问题

基于联系数正态模糊型多属性群决策问题可以描述为：决策方案集为X=｛X1， X2，…， Xm｝，决策的属性集为U=｛U1， U2，…， Un｝，决策专家群体集为D=｛D1， D2，…， Dl｝，专家的权重ν=｛ν1， ν2，…， νl｝，属性权重ρ=｛ρ1， ρ2，…， ρn｝。该多属性决策过程可以分为以下几个步骤。

2.1给定决策矩阵

第t个决策者关于属性对决策方案的决策矩阵为：

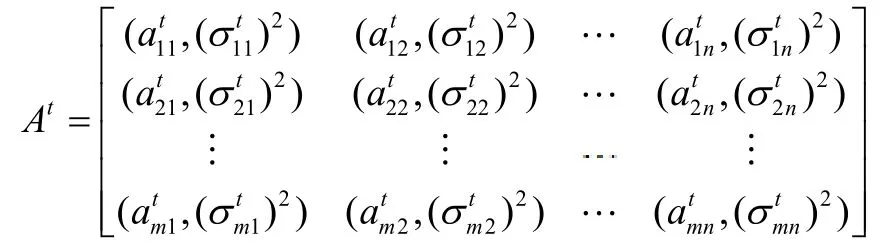
2.2将正态模糊数型决策矩阵转化为联系数型矩阵

2.3将联系数型矩阵标准化

为消除各属性的不同物理量纲对决策结果的影响，需要对原始决策矩阵进行规范化处理。

对效益型指标：

对成本型指标：

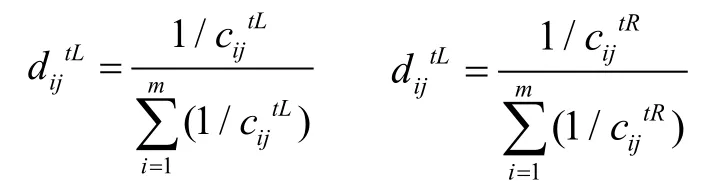
规范化后决策矩阵记为：

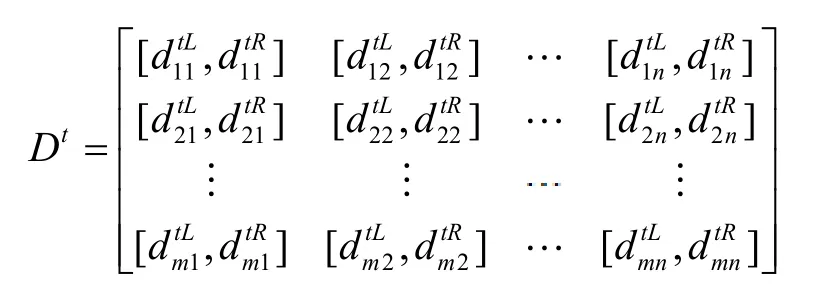
2.4 求决策群体中各专家的权重

因受到专家的地位、名望及所属专业和对决策问题的熟悉程度等因素的影响，使得每个专家不能同等的看待问题，同时个专家的权重也不能表示为一个精确的数值。在这里，我们根据专家的资历、经验等事先以正态模糊数的形式给出专家的权重，记为ν=｛ν1，ν2，…，νl｝，其中）。νt均值越大，则代表专家的能力越强，其方差越小，说明在专家进行评价时越不容易出错。所以权重νt的均值越大，方差越小的专家在评价方案时越可信。由此对第t个专家进行评分，依据可信值函数计算专家的可信分值，其中ε在评价专家权重时对待其评价值的态度，如果看中专家的期望，则取0.5＜ε＜1。利用可信分值，按下面的公式求得每个专家的权重：

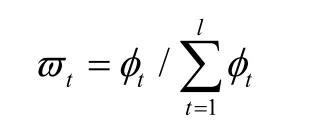
2.5求群体决策矩阵

2.6求各个决策方案的综合评价值并择优

利用联系数的乘法与加法运算，求出每个方案的综合决策联系数，并计算出决策模，决策模越大的方案越优。

3　实例分析

通常一些大学采用教学（U1），科研（U2）和服务（U3）这三个属性作为评估的一级指标（属性），属性权重分别为：ρ1，ρ2，ρ3，根据评估标准对5个学院X1，X2，X3，X4进行评估打分，各指标下的评估信息用正态模糊数给出.决策群体集D=｛D1， D2，D3｝，各专家的权重集：。

3.1给出决策矩阵

3位专家在不同的属性下对决策方案的决策值用正态模糊数来表示，决策矩阵如下。

3.2将决策矩阵转化为联系数，得下列矩阵

3.3确定专家权重

根据专家的经验及以往的资历等方面的了解，可以给出三位专家的正态模糊数权重为

ν=［ν1，ν2，…，νl］=［（75，52），（80，82），（90，62）］

利用可信度值公式可得三位专家的权重分别为：

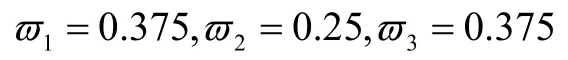
3.4求群体决策矩阵

3.5求各个属性的权重

ρ=［0.327 4+0.030 4i 0.356 4+0.010 9i 0.316 2+0.010 5i］

3.6求各个决策方案的综合评价值并择优

4　结 语

将正态模糊数理论引入到模糊多属性决策领域，复杂问题的解决将更加科学化、规范化。本文将正态模糊数转化为联系数简化了计算过程，最后以实例验证本文方法的可行性和有效性。

主要参考文献

［1］陈晓红，阳曦.一种基于三角模糊数的多属性群决策方法［J］.系统工程与电子技术，2008（2）：278-282.

［2］Hwang C L， Lin M J. Group Decision Making under Multiple Criteria：Methods and Application ［M］. Berlin： Springer-Verlag， 1987.

［3］曲文阁，周宏安.基于模糊语言评估和FOWA 算子的多属性群决策［J］.武汉理工大学学报：信息与管理工程版，2013（4）：623-626.

［4］梁昌勇，戚筱雯，丁勇，等.一种直觉模糊多属性群决策方法及其在群决策中的应用［J］.运筹与管理，2013（1）：41-47.

［5］李荣钧.模糊多属性决策理论及其应用［M］.北京：科学出版社，2002.

［6］桑广，吴涛.正态模糊数型多属性决策模型及其应用［J］.山西大学学报：自然科学版，2013（1）：34-39.

10.3969/j.issn.1673 - 0194.2015.20.049

O159；O225

A

1673-0194（2015）20-0061-02

2015-07-27