非线性带涂层球形复合介质的电势分布

郝艳花,张 英

（山西大同大学数学与计算机科学学院,山西大同 037009）

非线性带涂层球形复合介质的电势分布

郝艳花,张 英

（山西大同大学数学与计算机科学学院,山西大同 037009）

在复合介质满足电流密度J和电场强度E为Jα=σαE+χα|E|2E的关系下，应用摄动方法推导了在外加交流电电场E=E1sinωt+E3sin3ωt+E5sin5ωt的作用下,带球形涂层的非线性复合介质的电势分布公式。

非线性复合介质；摄动方法；交流电场；电势分布

近几年来，在不同的外加电场作用下，非线性复合介质的电势分布问题，其中球形和圆柱形复合介质因其特殊的结构，引起了诸多物理学家、数学家的重视。对于这类非线性复合介质,在外加电场作用下的有效性响应与外部电场有非常大的关系。Levy[1]和Hui[2]通过研究发现复合介质的高阶有效性响应受外加电场的谐和频率的影响;Gu[3]利用摄动展开方法推导出非线性复合介质在外加直流电作用下的有效电导率；Gu[4]和Wei得到了Kerr型非线性复合介质在低浓度、正弦电场作用下的有效的交流电响应公式;Wei研究推导了交流电场对随机放入到一个交流电场中球形复合介质的有效的交流电响应的影响；最近，Hao[5]和Chen[6]又利用摄动方法研究了带涂层非线性Kerr型复合介质有效性响应问题，假设外部交流电场Ea=E1sinωt+E3sin3ωt等等。

本文主要推导了带涂层球形非线性复合介质的电势分布公式，假定电流密度和电势边界条件下颗粒在内外两种杂质界面、基质界面、外层杂质上都是连续的，且电流密度J和电场强度E之间满足的关系如下：

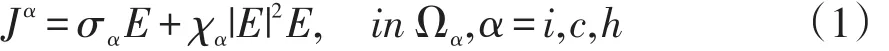
其中下标α=i指颗粒杂质内部，α=c指涂层，α=h指基质区域；Ωi表示颗粒杂质在内部所占空间区域,Ωc指涂层所占空间区域,Ωc指基质区域所占空间区域；σα是线性的介电常数，χα是非线性的介电常数，它们都与外加电场无关。电场强度E和电流密度J低频过程中分别满足为:∇×E=0和∇·J=0。由于介质球的极化，球面出现束缚电荷，以致电场强度E在球面不连续，ΔΦ=∇·∇Φ=-∇·E在球面上没有意义。由此我们只好先考虑球内、球外的电势，然后通过衔接条件再把两者在球面上衔接起来，即认为电势在球面上连续。

1 非线性交流电过程的摄动方法

假设外加电场为E=E1sinωt+E2sinωt+E5sin5ω沿ẑ轴正向作用于非线性复合介质,这里将球形杂质颗粒随机嵌入一弱非线性复合介质中，其内部半径为a,涂层半径为b,在本构关系中非线性项远小于线性项。

由于电场强度满足方程∇×E=0,故存在电势函数Φα(x,t),满足:

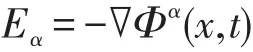
将x点处的电势可展开成如下形式：

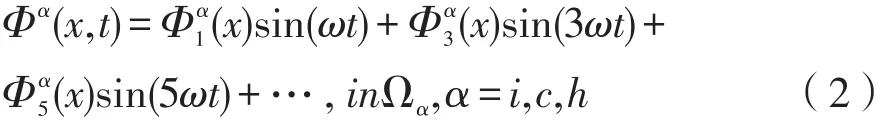
针对弱非线性复合介质中的电势分布问题，认为基质与杂质之间的接触是一种理想状态下的接触，忽略界面层对系统的影响，因此可采用摄动函数展开法来处理此类问题，电势函数展开式为：

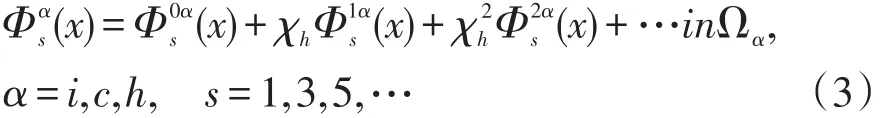
其中选取非线性的介电常数χh作为摄动参数，再利用电场强度和电势的关系将方程（2）和（3）代入到方程（1）中，即可得到电流密度J在杂质和基质区域的摄动展开函数式为：

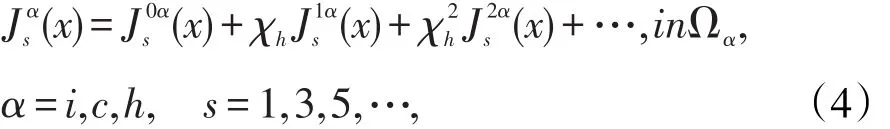
如果控制方程均适合（3）式中的每一项,则控制方程∇·J=0必成立，于是一组关于的方程也成立：

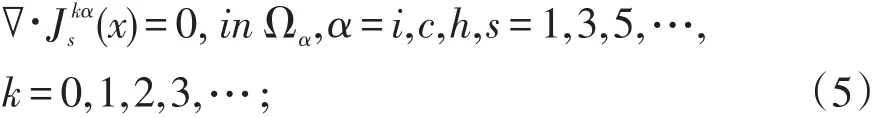
电势和电流密度的边界条件分别为：

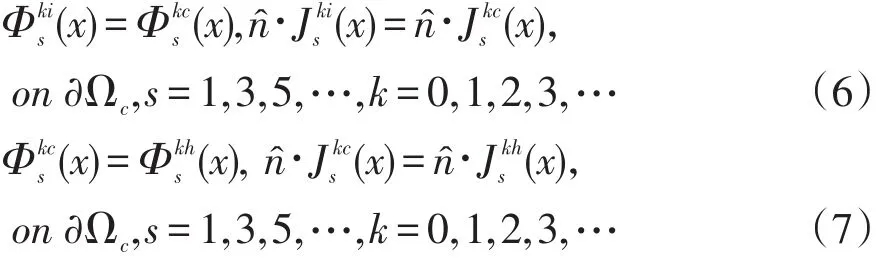
这里∂Ωi表示内外两层杂质界面，∂Ωc表示基质界面。

在无穷远处，电势满足下列关系：

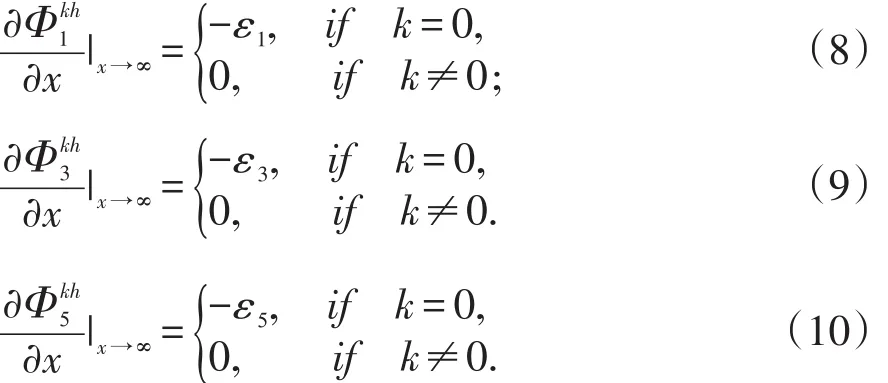
2 关于非线性复合介质的电势分布的研究

应用等式(4),(5),可得谐和频率分别为ω、3ω和5ω下零阶电势的本构方程关系为：

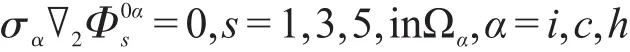
再应用衔接条件(8)、（9）、(10)，即可求得频率为的零阶电势：

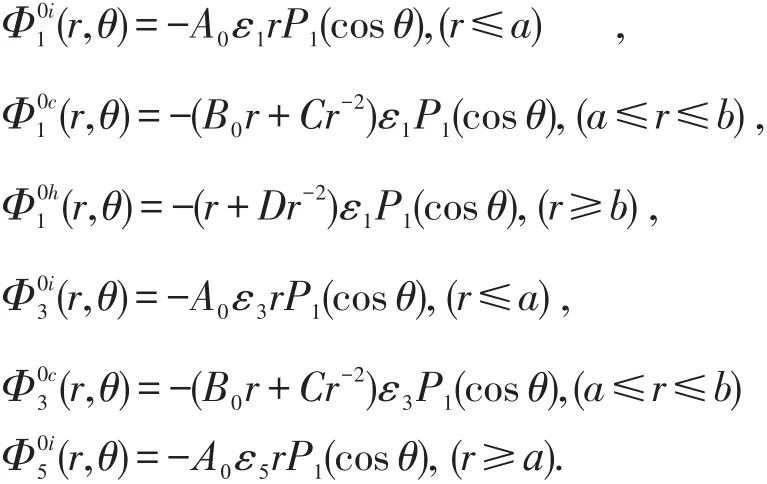
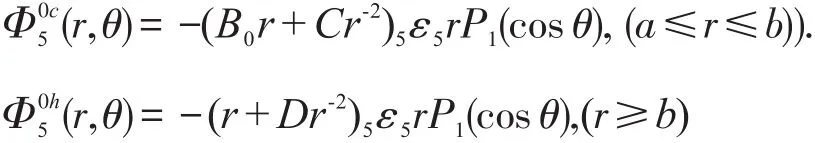
这里P1(cosθ)=cosθ是一阶Legendre多项式。其系数A0,B0,C,D和分别为:

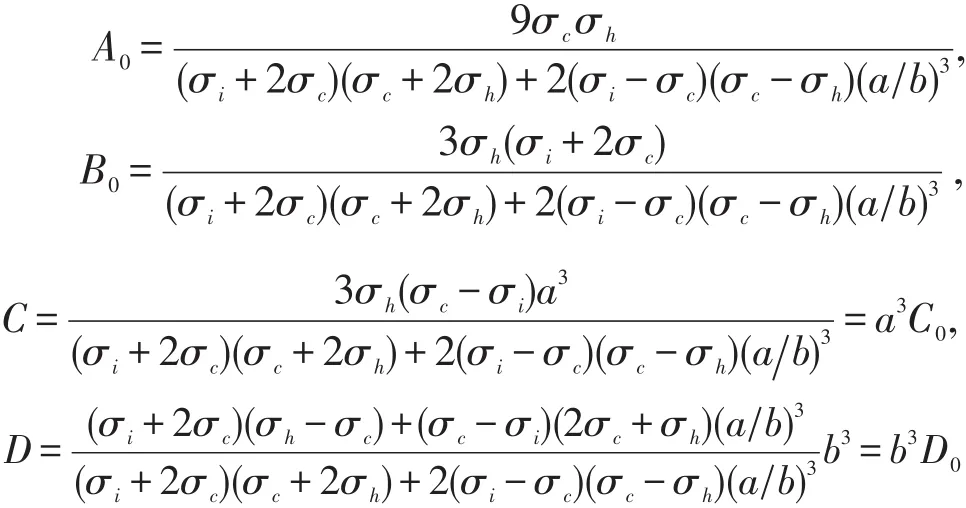
再利用频率ω、3ω和5ω的零阶电势,即可得频率为ω、3ω和5ω的一阶电势的本构关系式：

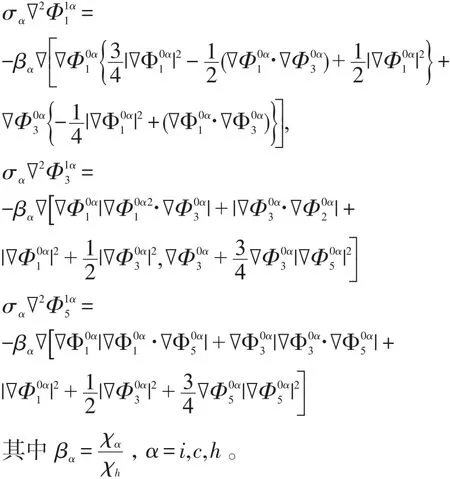
解上述方程且利用边界条件(6)～(10),可求到谐和频率为ω、3ω和5ω下，颗粒杂质的一阶电势分布公式：

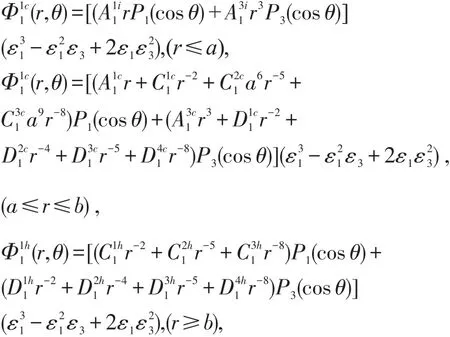
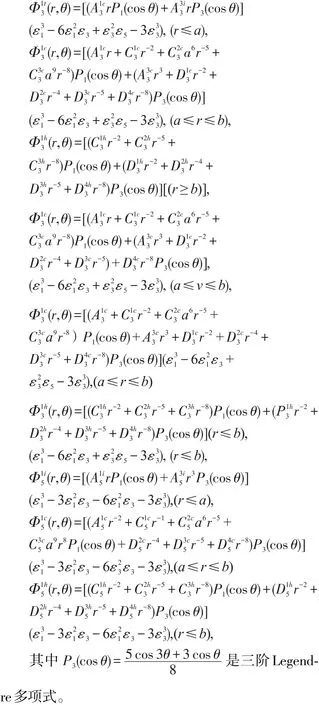
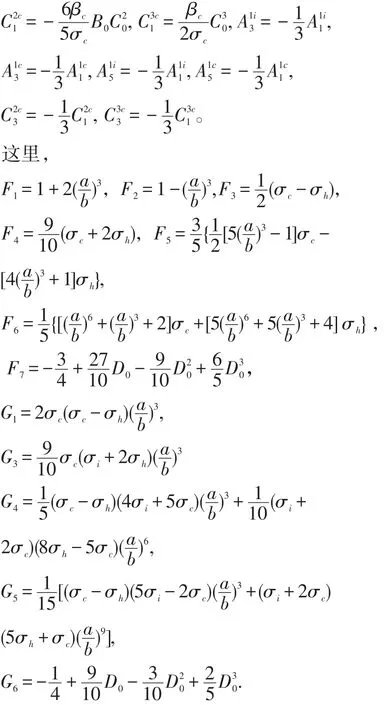
3 小结

低杂质浓度下，本文利用摄动方法推导了非线性带涂层球形复合介质在外部交流电电场E=E1sinωt+E3sin3ωt+E5sin5ωt作用下的电势分布公式，得到的只是一个数值解。对于本文的问题可做进一步的研究，利用同伦分析方法可研究高杂质浓度下，不同的外加交、直流电电场对非线性复合介质的影响，可得到响应的解析解。

[1]LEVY O,BERGMN D J,STROUD D G.Harmonic generation,induced nonlinearity,and optical bistability in nonlinear composites[J].Phys Rev E,1995(52):3184-3194.

[2]HUI P M,CHEUNG P.Second and third harmonic generations in random composites of nonlinear dielectrics[J].Phys B,2000(279):45-47.

[3]GU G Q,YU K W.Effective conductivity of nonlinear composites[J].Phys Rev B,1992,46(8):4502-4507.

[4]GU G Q,HUI P M,YU K W.A theory of nonlinear AC response in nonlinear composites[J].Phys B,2000(279):62-65.

[5]WEI E B,SONG J B,Gu G Q.Effective response of a non-linear composite in external AC electric field[J].Phys B,2002(324):322-328.

[6]WEI E B,TIAN J W,SONG J B.A theory of nonlinear AC response in coated composites[J].Chin Phys,2004,13(3):388-392.

Potential Distributions in the Coated Nonlinear Spherical Composite

HAO Yan-hua,ZHANG Ying
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)

Under the constitutive relations between current densityJand electric fieldEin the inclusion and host regions have the following forms:Jα=σαE+χα|E|2E,the potential in the coated nonlinear spherical composite is investigated under the action of an external AC electric field E=E1sinωt+E3sin3ωt+E5sin5ωtby using the perturbation method.

nonlinear composites；the perturbation method;AC electric field；the potential distributions

TN911.2

A

1674-0874(2015)05-0004-03

2014-06-17

山西大同大学科研基金项目[2011K6]

郝艳花（1973-），女，山西大同人，硕士，副教授，研究方向：计算数学。

〔责任编辑 高海〕