桥梁横向分布影响线的平面杆系有限元计算方法比较
2015-10-31周为恺
周为恺
(中国瑞林工程技术有限公司福州分公司)
桥梁横向分布影响线的平面杆系有限元计算方法比较
周为恺
(中国瑞林工程技术有限公司福州分公司)
桥梁横向分布系数平面杆系有限元法具有建模简单、快捷,计算快等优点。本文介绍了一种应用平面杆系有限元程序来分析桥梁横向分布影响线的计算模型,并用算例经过与其它横向分布电算软件及手算方法对比,验证其正确性和实用性。
桥梁横向分布系数;平面杆系有限元
前言
梁桥的上部结构由承重结构及传力结构“横隔梁、行车道板”两大部分组成,各片主梁靠横隔梁和行车道板连成空间整体结构,当桥上作用荷载时各片主梁共同参与工作形成了各片主梁之间的内力分布。在计算活载时,需要考虑活载在各片主梁间的分布。汽车荷载所引起的各片主梁的内力大小与桥梁的横断面形式、荷载的作用位置有关,因此求解汽车荷载作用下各主梁的内力是一个空间问题。目前采用的方法主要有桥梁三维空间分析与将复杂的空间问题转化为平面问题。前者主要采用1~3维结构分析通用程序,后者采用以平面杆系为主的桥梁结构专用分析程序配合荷载横向分布子程序结合应用。
由于桥梁受力计算采用三维空间整体分析虽然具有通用性,但也存在结构自由度多、工作量大,且仅靠应力分析很难进行配筋设计。因此桥梁计算时利用桥梁横向分布系数将复杂的空间问题转化为平面问题受到了广泛的使用。所以桥梁横向分布系数计算就显得尤其重要,在桥梁工程教材及其他各种专注中论述桥梁设计,大多均以桥梁横向分布系数计算为主。
目前桥梁工程教材介绍的荷载横向分布系数计算大致有以下一些方法:
(1)杠杆法;
(2)梁格法,包括刚性横梁法(也称偏压法)以及修正刚性横梁法(修正偏压法)、弹性支承连续梁法;
(3)梁系法,包括铰接板法、刚接板法、铰接梁法、刚接梁法;
(4)板系法,如比拟正交异性板法(G-M法)。
以上荷载横向分布系数计算方法在一般桥梁书籍中大多数介绍都以手算为主,本文介绍一种应用平面杆系有限元程序来分析桥梁横向分布影响线的计算模型。采用带有平面有限元计算功能的软件即可实现对桥梁荷载横向分布系数进行快速计算、校核。
平面杆系有限元法求解横向分布系数计算模型如图1。
其中的集中竖向弹簧支承刚度Kω和扭转支承刚度Kθ可以由下式得出:
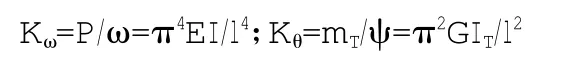
式中:I-为抗弯惯性矩;IT-为抗扭惯性矩;G取0.43E。单集中荷载P=1作用于某块板时计算得出的各板块支承反力即为该板块的荷载横向分布影响线竖标值η。当各板块之间具有可靠的横向连接时,即需考虑主梁的抗扭刚度时只要把以上模型的主从节点取消,变为刚性连接的单元,就形成刚性横梁法荷载横向分布计算模型。以下举例验证其正确性和实用性:

图1 铰接板桥荷载横向分布计算模型
[例1]如图2所示的简支梁桥,其计算跨径l=24.0m,桥面净宽为10.25m+2×0.5m,横隔梁中距为6m,混凝土强度为C40。
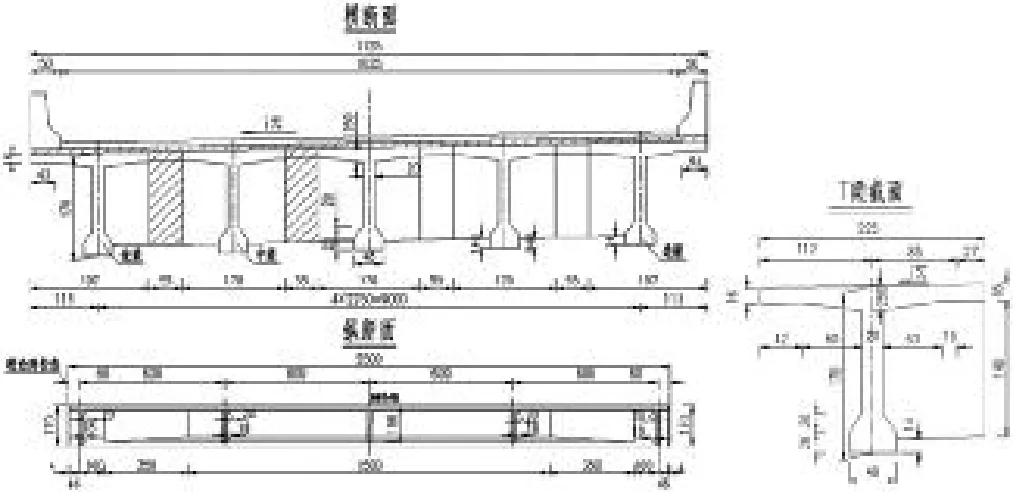
图2 结构基本尺寸图
问题一:将T梁的翼板视作铰接板,计算1号边梁的汽车荷载横向分布影响线竖标。
问题二:考虑主梁抗扭刚度时,计算1号边梁的汽车荷载横向分布影响线竖标。
解:问题一
(1)建立平面有限元法计算模型,其中翼板厚平取16cm,单元板宽取b1=100cm,刚臂断点(2、5、8、11、14号节点)距板中心的高度h近似取等于主梁全高,即h=170cm。
(2)计算Kω和Kθ
采用Midas Civil截面特性计算器SPC计算T形截面特性如下:

代入得:Kω=π4EI/l4=π4×3.3×107×0.276395/244=2677.9kN/m
Kθ=π2GIT/l2=π2×0.43×3.3×107×0.01386/242=3369.9kN/m(如图3)
(3)平面杆系有限元法计算结果
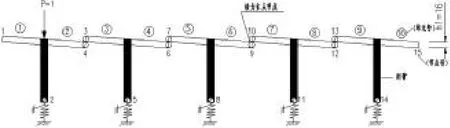
图3 铰接T型梁计算模型
表1列出1、2、3号梁上分别在P=1作用时各竖向集中弹簧支承的垂直反力,即各梁的荷载横向分布影响线竖标。

表1 1、2、3号T形梁的荷载横向分布影响线竖表
(4)采用桥梁博士3.0横向分布子程序铰接板梁法计算结果如下:
影响线数值:

与平面杆系有限元法计算结果对比十分接近。
解:问题二
(1)计算横隔板的等效板厚,此时须对中横隔梁进行等效处理,使之成为“拟无横隔板的肋梁桥”,计算方法为:先计算下图阴影部分抗弯惯性矩I横,由于本例L1=6m,固I横=0.168217m4,得等效板厚为he=(12×I横/L1)-3=(12×0.168217/6)-3=0.6955m。

图4 中横隔梁等效处理后的计算截面
(2)将铰接T型梁计算模型中的主从节点去除,将翼缘板厚度改为he=0.6955m,其它条件不变,如图5。
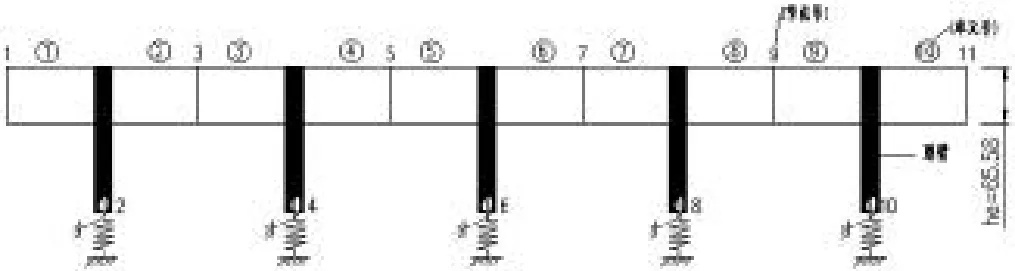
图5 刚接T型梁计算模型
(3)平面杆系有限元法计算结果
表2列出1、2、3号梁上分别在P=1作用时各竖向集中弹簧支承的垂直反力,即各梁的荷载横向分布影响线竖标。

表2 1、2、3号T形梁的荷载横向分布影响线竖表
(4)采用桥梁博士3.0横向分布子程序刚接板梁法计算结果如下:
影响线数值:

与平面杆系有限元法计算结果对比十分接近。
[例2]等截面连续箱梁截面见图6,桥孔布置:4×30m,交角90°,采用50号混凝土,E=3.35×104MPa,G=0.43E(剪切弹性模量),试用修正偏心压力法及平面杆系有限元法计算中跨边腹板荷载影响线竖标值。
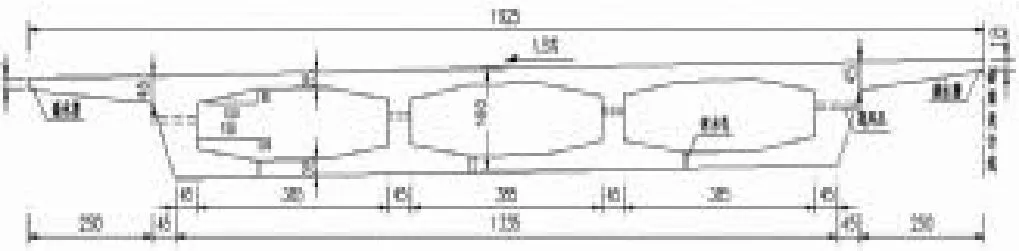
图6 箱梁横断面图
解:(一)采用修正偏心压力法计算中跨边腹板荷载影响线竖标值。
(1)计算截面刚度
采用Midas Civil截面特性计算器SPC计算截面特性如表3。
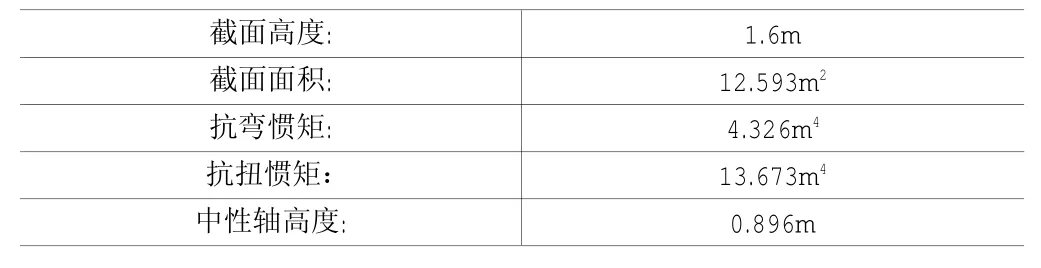
表3
(2)计算抗弯及抗扭刚度换算系数:
①抗弯刚度换算系数K的计算:
K=δ0/δ,中跨:边跨=1:1由《梁桥下册》P204页等截面连续梁等效简支梁刚度修正系数表4。

表4
内插得:

表5
②抗扭刚度换算系数K′的计算:
取K′=1
(3)按修正偏压法计算荷载横向分布系数
①计算公式:

式中:β——抗扭修正系数;
P——外荷载之合力;
e——P对桥轴线的偏心距;
ai——主梁I至桥轴线的距离。
②计算β

式中:∑It——全截面抗扭惯距(13.673);
Ii——主梁抗弯惯距Ii=KIi′。
将截面划分为τ梁和I梁,划分原则:保持将两截面中性轴与全截面中性轴位置一致。
τ梁和I梁顶板尺寸在两肋间平均划分。由于中性轴位置不变,可计算底板尺寸,尺寸图如图7所示。

图7

采用Midas Civil截面特性计算器SPC计算τ梁和I梁抗弯惯距输出结果如表6。
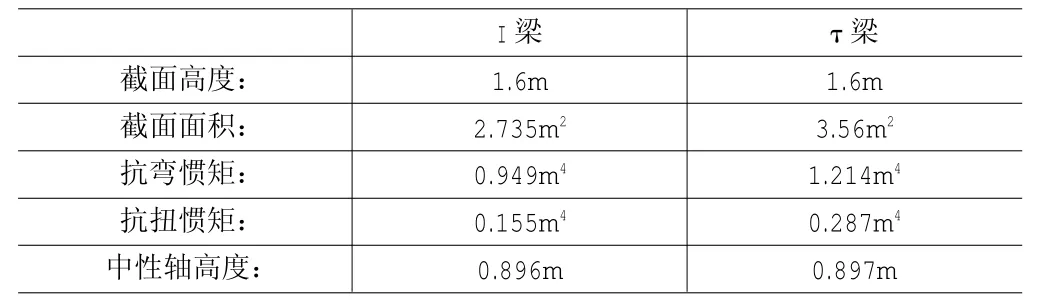
表6

③计算边腹板横向分布影响线竖标值
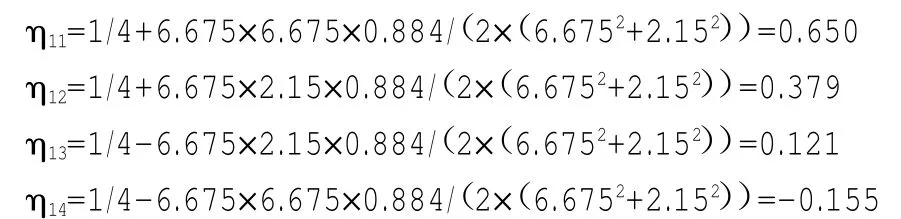
(二)采用平面杆系有限元法中跨边腹板荷载影响线竖标值。
①计算Kω和Kθ
计算修正后腹板抗弯刚度和抗扭刚度:
边腹板:I边=1.214×1.86=2.258m4IT边=0.287m4×1=0.287m4
中腹板:I中=0.949×1.86=1.765m4IT中=0.155m4×1=0.949m4
代入得:Kω边=π4EI/l4=π4×3.35×107×2.258/304=9097kN/m

②建立平面杆系有限元法模型(如图8)
本例箱梁由于横向抗弯刚度很大,因此模型中he高度近似取梁高1.6m。当然也可以计算出箱梁横向平均抗弯惯性矩,再求得等效翼缘板厚度he。实际计算最终结果相差不大。
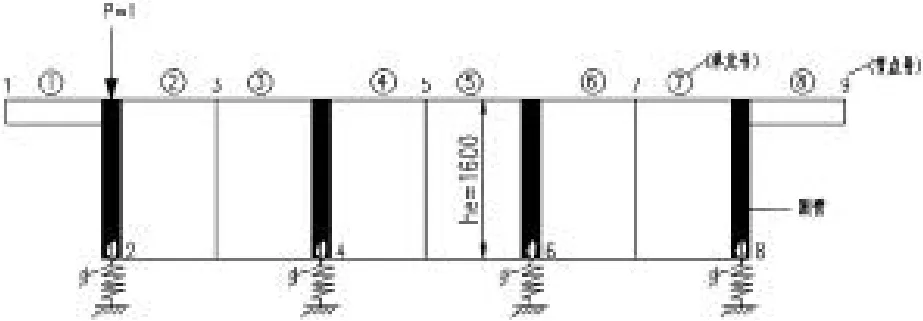
图8
③平面杆系有限元法计算结果
表7列出1号梁上分别在P=1作用时各竖向集中弹簧支承的垂直反力,即各梁的荷载横向分布影响线竖标。

表7
与修正偏压法计算结果相差不大,如果按规范中的标准车辆对以上模型进行横向加载,并取轴重PH=1/2,所求各支撑的最大支反力,即为每片梁荷载横向分布系数。
结论:在没有其它桥梁荷载横向分布系数电算程序时,桥梁横向分布系数平面杆系有限元法绝对是计算桥梁横向分布系数首选方法,它与手算法对比可以省去查表、内插等繁琐的计算步骤,也可以作为其它荷载横向分布系数计算方法一种校核工具。
[1]邵旭东,程翔云,李立峰.桥梁设计与计算.人民交通出版社,2012,11.
[2]胡肇滋.桥跨结构简化分析——荷载横向分布.人民交通出版社,1996,12.
[3]周先雁,王解军.桥梁工程.北京大学出版社,2008,1.
U448.21+5
A
1673-0038(2015)21-0209-03
2015-5-6
