重费米子二流体理论

2015-10-31杨义峰谢能李宇

物理学进展 2015年5期

关键词：费米子导带局域

杨义峰，谢能，李宇

1.中国科学院物理研究所，北京凝聚态物理国家实验室，北京100190 2.量子物质科学协同创新中心，北京100190

重费米子二流体理论

杨义峰1，2∗，谢能1，李宇1

1.中国科学院物理研究所，北京凝聚态物理国家实验室，北京100190 2.量子物质科学协同创新中心，北京100190

强关联电子同时表现出局域和巡游的二重性，这是量子力学波粒二象性在凝聚态物理领域的表现，也是导致强关联材料中各种新奇量子效应的根源。本文以重费米子材料为例，探讨强关联f电子在该类材料中局域和巡游二重行为的实验表现，重点介绍重费米子的二流体唯象理论。这一理论成功解释了众多先前无法解释的实验现象，揭示了重费米子体系复杂行为背后的统一物理起源，为理解强关联系统包括铜氧化物和铁基超导材料中电子的奇异行为提供了一种新的思路，亟待更加深入的理论和实验探索。

强关联电子；重费米子；二流体理论

I.重费米子物理简介

描述固体材料中电子的微观行为是凝聚态物理的核心问题。当电子间的库仑相互作用较弱时，电子在晶格中的运动可以近似采用单电子图像描述，在此基础上发展起来的经典能带理论成功解释了普通金属、绝缘体和半导体的基本性质。但是在包含过渡族金属元素的d电子或镧系/锕系元素的f电子体系中，电子间通常具有较强的库仑相互作用，导致单电子近似失效，此时众多强关联电子之间的协同运动使得材料在低温下呈现出许多新奇的量子现象[1]，如高温超导、庞磁阻、重费米子等等。发展超越经典能带理论的强关联电子理论，是目前凝聚态领域的一个重要前沿课题。

在这篇文章中，我们简要介绍一类传统的强关联电子体系，即重费米子体系。与常规金属不同，重费米子材料在低温下具有非常大的比热系数，是铜、金等常规金属的比热系数（∼1 mJ/mol K2）的几百以至上千倍。按照朗道的费米液体理论，如此大的比热意味着材料中准粒子的有效质量可以达到自由电子质量的几百乃至上千倍，所以这类材料被统一称作重费米子或重电子材料[2，3]。目前常见的重费米子材料一般为包含Ce，Yb，U等稀土或锕系元素的f电子金属化合物，也有少量的d电子材料如LiV2O4[4]和CaCu3Ir4O12[5]等。在这些材料中，局域在晶格上的f或d电子形成局域磁矩，与自由运动的导带电子在低温下发生集体杂化，产生运动迟缓的复合准粒子，实验上表现出较大的有效质量。

由于电子的特征能量与其有效质量成反比关系，因此重费米子材料的特征能量尺度很低，一般只有10∼100 K的量级，极易通过压力、磁场、掺杂等实验手段进行调控。最近十多年来，随着材料制备水平和实验技术的提高，重费米子领域涌现出大量的新材料、新物理，不仅仅在很多材料中都观察到了非常规超导、非费米液体、量子临界等重要的强关联电子现象，还发现了如CeCu2Si2中的高压超导相[6]，CeCoIn5中强磁场诱导的Q-相[7]，URu2Si2中的隐藏序[8]，SmB6中的拓扑表面态[9，10]等具体材料中丰富多样的奇异电子态。这些发现极大地充实了凝聚态物理的研究内容，成为探索强关联电子现象和物理本质的重要研究对象。

重费米子材料的发现源自20世纪上半叶对金属中磁性杂质的散射效应的研究[11]。1930年，德国物理学家Meissner和Voight在实验上[12]观测到金（Au）的电阻在温度10 K附近出现极小值，10 K以下反常增大。这一反常的电阻极小值现象和超导的零电阻现象并驾齐驱，引起了实验和理论上的极大兴趣，成为当时固体物理学中的两大著名难题。但是直到1964年，在超导问题被Bardeen、Cooper和Schrieffer等人解决数年后，才由美国贝尔实验室的Sarachik等人在实验上给出了最确定性的证据，将电阻的极小值问题与金属中磁性杂质对导带电子的散射联系起来[13，14]：他们在钼铌合金（MoxNb1−x）中掺入1%铁（Fe）杂质，发现当Mo的浓度增加到一定值时，Fe杂质会表现出磁性，同时电阻曲线中出现极小值，两者之间存在直接关联。同年，日本科学家Kondo分析了导带电子与磁性杂质之间由于反铁磁耦合导致的自旋翻转散射，对散射过程进行微扰处理，在相互作用的三阶项上发现了电阻随温度降低呈现出−logT的发散行为，这一贡献与声子散射的贡献结合起来，解释了金属中电阻的极小值现象[15]。此类自旋翻转散射后来被称为Kondo散射。

Kondo散射有一个重要的特征温度，TK，称为Kondo温度，通常TK≈ρ−1e−1/Jρ，其中ρ是费米面附近导带电子的态密度，J是磁性杂质上的局域磁矩与导带电子自旋之间的反铁磁交换耦合强度[16]，本文中Boltzmann常数均设为1。在TK之上，导带电子与局域磁矩发生自旋翻转散射，其高阶相干过程的叠加对有效散射强度产生对数修正，随温度降低而增强，最终在TK处发散。因而在TK之下，体系处于强耦合区，微扰展开的处理方法失效，局域磁矩与导带电子之间形成自旋单态，导带电子在磁性杂质周围形成屏蔽云。电阻在接近零温时从对数发散的温度依赖关系转变为T2的依赖关系并趋于饱和，表现为局域费米液体的行为。同时由于重整化效应，f电子能级被重整化到费米能附近，在态密度上出现共振态，导致很大的低温比热系数。

Kondo问题在强关联电子系统的研究历史上发挥了非常重要的作用[17]，重费米子现象的发现就是其中一个重要的例子。1975年，美国贝尔实验室的Andres等人[18]发现Ce的金属化合物CeAl3在温度低于0.2 K时具有很大的线性比热系数（C=γT，γ= 1620 mJ/mol K2），同时电阻表现为典型的费米液体行为（∆ρ=AT2，A=35µΩ cm/K2），表明其中的准粒子具有很大的有效质量，这是实验上发现的第一个重费米子材料。1979年，德国科学家Steglich等[19]在重费米子材料CeCu2Si2中发现超导，无法用传统的基于电声耦合的BCS（Bardeen-Cooper-Schrieffer）理论解释。此前众多实验都表明磁性杂质对（常规）超导具有很强的破坏作用，因此一般认为超导与磁是不相容的，而Ce在这里为+3价，最外层有一个f电子，高温下表现为磁性离子，这一发现改变了人们对超导与磁的关系的认识。随着类似的超导现象在UBe13[20]和UPt3[21]等更多重费米子材料中陆续被发现，非常规超导现象开始引起了理论和实验上的关注，与随后的铜氧化物高温超导和铁基超导一起，逐渐开启了三十多年来非常规超导研究的大门。

在大多数Ce基重费米子材料中，Ce为+3价，最外层只有一个f电子，由于很强的局域库仑排斥作用，f电子的电荷涨落被抑制，同时考虑到晶体场基态（二重态），在低温下表现为自旋1/2的局域磁矩。这些磁矩在晶格点阵上周期排布，形成周期性的自旋晶格，并与导带电子之间发生集体耦合，不同于单杂质的情况。因而对重费米子物理的理论研究，文献中经常采用所谓的Kondo晶格模型[3]

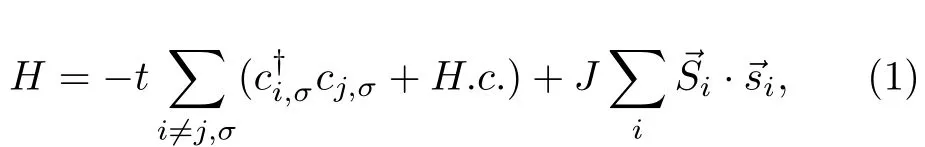
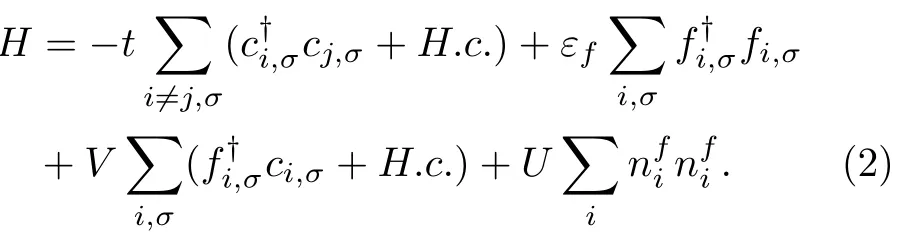
模型中第一项为导带电子的跃迁项，第二项为f电子的能级，第三项是导带电子和f电子的杂化项，第四项为f电子之间的局域库仑排斥。一般情况下，这两个模型目前尚无法严格求解，只能采用近似方法。

1977年，美国斯坦福大学的Doniach利用平均场近似分析了Kondo晶格模型的基态性质[22]。由于局域磁矩对导带电子的极化作用，晶格上相邻磁矩间会产生间接的磁交换相互作用，即Ruderman-Kittel-Kasuya-Yoshida（RKKY）相互作用[23∼25]：TRKKY∝J2ρ[26]。Doniach提出体系的基态取决于RKKY作用与Kondo效应的竞争。如图1（a）所示，在Kondo耦合J较小时，RKKY作用占主导，体系表现为磁性基态，随着J的增加，Kondo温度指数增加，最终抑制了RKKY作用，导致体系从磁有序态过渡到了费米液体态（Kondo效应主导）。这一图像定性地解释了许多材料的实验相图，得到了广泛的认可。

80年代，Read，Newns[27]和Coleman[28]等人发展了所谓的隶玻色子（slave boson）近似方法，用于处理单杂质Kondo问题，后来被推广到Kondo晶格模型[29∼31]。如图1（b）所示，在这一近似下，局域的f轨道由于与导带电子的Kondo耦合被重整化到费米面附近，形成平坦的f能带，进而与导带发生杂化，形成杂化能带，其准粒子具有较大的有效质量。这一简单的杂化图像可以解释光电导中的杂化能隙等一些实验现象，但忽略了f电子强关联多体作用导致的复杂行为如量子临界现象等。要描述这些现象，必须要考虑f电子之间的关联。清华大学的张广铭等人[32，33]在这一方面作了很多工作，他们推广了平均场方法，考虑进f电子之间的磁性关联及超导配对，得到Kondo单态和磁有序态可以共存等重要结论。

超越简单平均场近似的理论工作目前主要有两类：一类是基于强关联方法的数值计算，如斯其苗等人利用扩展动力学平均场方法（EDMFT）研究Kondo晶格模型，解释YbRh2Si2等材料中发现的局域量子临界现象[34]，Kotliar等人结合密度泛函理论（DFT）和动力学平均场方法（DMFT）研究CeIrIn5等材料，以解释f电子随温度降低从局域到巡游的转变过程[35，36]，Assaad等人也利用辅助场量子蒙特卡洛方法（AFQMC）研究了二维半满Kondo晶格模型的基态相图和有限温度的自旋及电荷动力学[37]等；另一类是在平均场近似基础上引入高阶的量子涨落效应，如Senthil等人[38]和Ppin等[39]考虑了U（1）规范涨落和Kondo玻色子涨落对量子临界行为的影响，Abrahams和Wlfle提出了临界准粒子理论，以解释YbRh2Si2等重费米子金属中的量子临界标度律[40∼42]等。

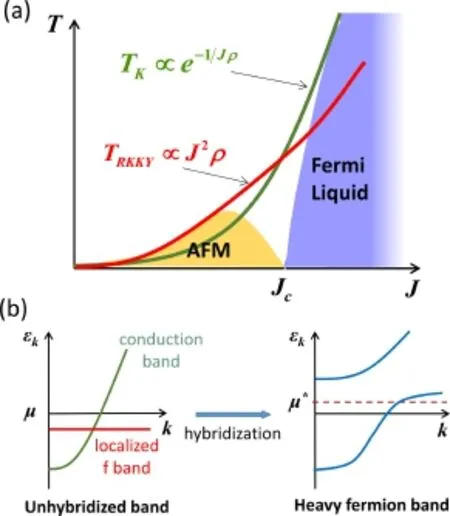
图1.(a)重费米子Doniach相图。随着Kondo耦合系数J的增加，Kondo效应增强，RKKY相互作用逐渐被抑制，体系逐渐从反铁磁相（AFM）过渡到费米液体（Fermi Liquid）。(b)重费米子杂化图像。局域的f电子能带由于Kondo耦合被重整化到费米面附近，与导带杂化形成比较平坦的杂化能带

这些工作从不同角度研究重费米子物理，但迄今为止还没有一个能够比较全面地解释重费米子物理的理论。如何系统梳理五花八门的实验现象，辨析背后物理的共性和个性，是理解重费米子物理的关键。考虑到这一点，我们采取了不同的思路，结合实验探索重费米子材料中具有普适性的物理行为。我们认为，f电子同时具有局域和巡游的二重行为，这种二重性可能是导致重费米子材料中丰富多变的演生现象的根本原因。在此基础上，我们发展了重费米子的唯象的二流体理论，较好地解释了许多先前无法解释的实验现象，形成了对重费米子物理的一些新的认识。这篇文章将介绍相关的研究工作和最新进展：第II部分从一般的角度介绍凝聚态物理中的二流体现象，第III部分详细论述重费米子二流体理论的基本框架和内容，第IV部分介绍最新的实验验证，第V部分讨论二流体现象的微观理论探索，最后是一个简短的总结和展望。

II.二流体理论的历史背景

二流体图像最早用于描述超导和液氦超流现象。1934年，荷兰物理学家Gorter和Casimir提出了超导电性的二流体唯象模型[43]，认为超导体中存在正常电子和超流电子两种电子，两者互相渗透而又独立运动。正常电子和金属中的自由电子一样受到晶格和其他电子的散射，不形成超导；超流电子则不受散射，贡献电流而不产生电阻。超导体内稳定电流的存在要求超导电子不能被外电场加速，因此超导体内电场为零，即使正常电子也不贡献电阻，不产生能耗，从而解释了超导的零电阻行为。

液氦超流现象发现后，匈牙利科学家Tisza于1938年提出了超流相（4He II）的二流体模型，苏联科学家Landau随后作了改进[44]。氦元素原子核内有两个质子，存在氦3和氦4两种同位素。氦4包含两个中子，是玻色子，在临界温度Tλ=2.18 K以下发生玻色–爱因斯坦凝聚，体系从正常流体的4HeⅠ相转变为无粘滞的超流体4He II相。二流体模型认为4He II相由两种流体组成，分别对应于基态的超流成分和由元激发组成的正常成分。在Tλ温度以上，即4He I相，所有流体都为正常流体；在Tλ温度以下，正常流体成分随温度降低逐渐转变为超流成分，最终在绝对零度时完全超流。4He II的物理性质由两种成分共同决定，成功解释了4He II毛细管实验中呈现出的超流现象、圆盘实验中呈现出的阻尼运动、以及机械致热效应等看似互相矛盾的各种奇异现象。

近些年来，强关联电子系统中的二流体现象也逐渐引起了人们的关注。2004年，Nakatsuji等人在分析重费米子材料Ce1−xLaxCoIn5的比热和磁化率数据时，发现f电子的磁性比热和磁化率均可以分为两个部分，如比热可以写为[45]：

其中CKI为实验测得的稀磁极限下（x=0.97，0.98）的比热，CHF为巡游重电子的比热贡献，f（T）是两种贡献的相对权重。据此，他们提出f电子的行为可以用一个类似的二流体模型描述。同年，Curro等人[46]发现这一模型也可以用来解释奈特位移对静态磁化率线性关系的反常偏离。2008年，Yang和Pines等人[47，48]发现在奈特位移、霍尔系数、点接触谱等多种物理量中均具有普适的温度演化行为。他们随后对二十多种重费米子材料的不同实验结果，如电阻、磁化率、核磁共振（NMR）、霍尔系数、光电导等，进行了系统分析，发现这些结果中的反常行为均起源于巡游重电子的演生行为，可以用二流体模型统一解释。2012年，他们进一步发展了这一想法，提出了比较系统的二流体唯象理论框架[49]，给出了两种流体更为具体的描述，即由部分杂化的局域f磁矩构成的自旋液体和由集体杂化形成的巡游重电子，认为两种流体的共存与竞争是描述重费米子物理的本质，并在此基础上定量地解释了众多实验现象，包括低温磁性序与超导共存、量子临界行为等等。

铜氧化物和铁基超导材料的正常态也具有类似的二流体行为。上世纪90年代前后，Johnston[50]及Nakano等[51]发现La2−xSrxCuO4−y的磁化率呈现普适的标度行为；2006年，Barzykin和Pines基于这些实验，提出铜基超导的正常态也可以描述为两种流体，即由局域磁矩形成的自旋液体和由巡游准粒子形成的费米液体[52∼54]。他们由此解释了铜氧化物中的NMR等系列实验结果，并预言赝能隙现象与最近邻局域磁矩间的反铁磁耦合存在密切关系。铁基超导材料中正常态电子的二流体行为的实验证据主要来源于NMR实验和非弹性中子散射（INS）实验。中国人民大学的于伟强研究组通过对Tl0.47Rb0.34Fe1.63Se2和NaFe0.94Co0.06As等铁基超导材料的奈特位移及自旋–晶格弛豫率的测量分析[55，56]，发现体系中存在类似的由巡游电子和局域磁矩构成的两种共存流体；中国科学院物理研究所的戴鹏程研究组[57，58]则在掺杂的BaFe2As2的中子散射实验中，发现了同时存在的由巡游电子产生的低能激发和由局域磁矩产生的高能激发，提出超导电性可能起源于高能磁激发诱导的低能巡游电子配对。最近，清华大学的翁征宇研究组[59]也从理论上探讨了铁基材料中的二流体现象，认为体系中同时存在局域磁矩形成的自旋液体和巡游电子，二者之间通过洪德（Hund）耦合相互影响，产生了丰富的物理现象。

这些工作表明，二流体现象是强关联电子系统中普遍存在的现象，可能反映了强关联电子的本质物理性质，是发展强关联电子理论要考虑的一个重要因素，值得理论和实验的深入探讨。

III.重费米子二流体理论

在这一章中，我们将详细介绍Yang和Pines等人发展的重费米子二流体理论[47∼49]，分为三个部分：二流体基本模型（A节）；正常态反常物性（B节）和对低温反铁磁、超导等有序态的解释（C节）。

A.模型

重费米子材料中f电子的局域和巡游的二重性质在实验上有很多表现，这些实验现象构成了二流体理论的物理基础。以CeRhIn5为例，在一定的压力区间内同时存在局域反铁磁序与超导，核四极矩共振（NQR）实验[60]证实两种序微观共存，Ce3+离子上的一个f电子同时参与反铁磁和超导两种宏观量子态，表现出局域和巡游的二重性。在二流体理论中，这种局域和巡游的二重性被简化描述为由f电子形成的两种近似独立的流体，一种是由局域自旋构成的自旋液体，另一种是由巡游重电子构成的Kondo液体。

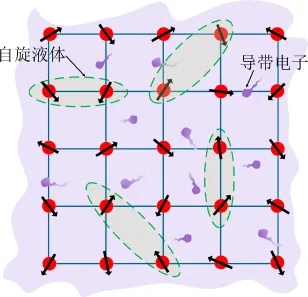
图2.Kondo晶格模型示意图

从Kondo晶格模型出发，这一图像有着自然的物理起源。如图2所示，Kondo晶格模型天然包含两种组分，即局域的f电子磁矩和巡游的导带电子。高温时，局域磁矩和导带电子之间的散射很弱，两种组分近似独立；随着温度降低，两者之间的有效耦合逐渐增强，导带电子由于受到自旋晶格的相干散射，运动变得迟缓，表现出重电子的行为；另一方面，晶格自旋也受到导带电子的屏蔽，有效磁矩被削弱，发生重整化效应。整个体系可以近似看作是缓慢运动的重电子和被集体杂化修正的晶格自旋液体两种流体的微观均匀混合。一般情况下，两种效应同时发生并相互纠缠，两种组分不能视作独立的流体。但是如果两种流体的运动在空间（动量）或时间（能量）上具有不同的特征尺度，则类似于固体中区分晶格与电子运动的Born-Oppenheimer近似，就可以将两者近似视作不同的流体，加以区分处理。

重电子在物理上对应于导带电子与晶格自旋涨落耦合形成的复合粒子。f电子从局域到巡游的转变不是相变，而是在广阔温度区间内发生的渐进行为。在这个温度区间内，f电子与导带电子发生集体杂化，由于量子纠缠而形成了复合的巡游重电子态，导致f电子逐渐退局域化，表现出巡游和局域的二重性质。Yang和Pines发现f电子从局域到巡游的转变随温度具有普适的演化行为，其中参与形成Kondo液体的f电子权重为[47]：

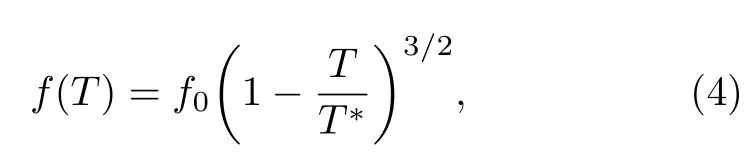
其中f0反映了集体杂化的效率，依赖于外界参数如压力、磁场等；特征温度T∗是一个重要的参量，后面会详细讨论。Kondo液体中准粒子的有效质量随温度演化遵从：

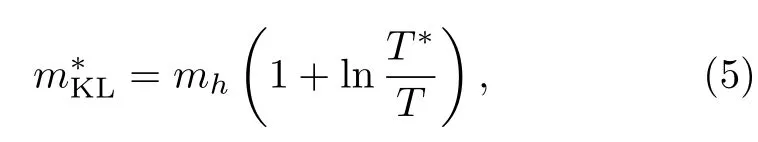
其中mh是准粒子在T∗处的有效质量。两式结合给出了巡游重电子的态密度随温度演化的普适标度律：

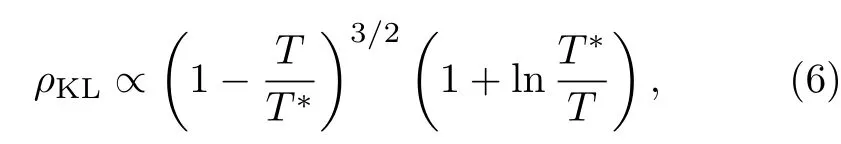
这种普适性表明f电子从局域到巡游的转变过程具有不依赖于材料细节的普适物理规律。后面我们会看到，重电子这一性质在很多实验中都有表现。

与巡游部分不同，局域自旋液体的行为则依赖于晶格结构等材料细节。在平均场近似下，考虑集体杂化对f电子磁矩的屏蔽作用，局域自旋液体的动力学磁化率χl可以近似写为[49]

其中fl=1−f（T）为f电子参与形成局域自旋流体的权重，χ0=C/T（C是居里常数）是孤立的f电子局域磁矩的磁化率，z为配位数，γl为自旋弛豫率，Jq是局域f磁矩间的RKKY交换耦合系数，其具体形式依赖于晶格结构，不具有普适性。

可以想象在实际材料中，两种流体彼此约束，既共存又竞争，随温度或其他外界参量具有不同的变化行为，两种行为的叠加导致实验的观测结果复杂多变，难以总结出一般性的规律，长期以来无法给出比较系统的解释。

为了理解Kondo液体的物理起源，Yang等人对（6）式中的特征温度T∗进行了系统深入的分析[48]。他们发现在大部分重费米子材料中，T∗比相应的单杂质Kondo温度TK高一个数量级，意味着T∗应有不同于Kondo温度的物理起源。基于实验考虑，Yang等人猜测T∗源自局域f磁矩间的RKKY相互作用。图3给出了十多种重费米子材料中的T∗与单杂质TK的对比[48]。取T∗=cJ2ρ（其中ρ是导带电子态密度，c是依赖于材料的常数，kB为Boltzmann常数，可以设为1），则由TK=ρ−1e−1/Jρ，必然要求

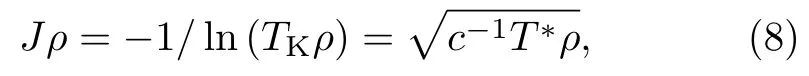
其中ρ可以由对应的非磁性材料（如CeCoIn5对应LaCoIn5）的低温比热系数γ得到，Kondo温标TK则可以通过稀磁极限下的电阻、比热等测量结果，在考虑到掺杂引起的体积修正后估计。如Ce0.01La0.99CoIn5，其中Ce离子间的f电子自旋相互作用可以忽略，从而表现为单杂质Kondo效应，通过适量加压可以对体积改变进行修正。由于J与TK之间是对数依赖关系，TK的实验误差对J的估计值影响很小。

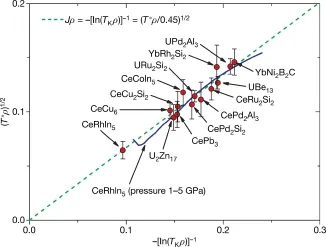
图3.一些重费米子材料的T∗、TK和态密度ρ的关系[48]。其中虚线由公式(8)给定，实线为CeRhIn5从1 GPa到5 GPa的结果，图中误差表示T∗估计值的不确定性

从图3中可以看出，这些材料虽然具有不同的晶格结构和晶体场基态，但是实验所得的T∗和TK都近似满足公式（8），并且具有相近的比例系数：c≈0.45。特别是图3中还给出了CeRhIn5随压力变化从1 GPa到5 GPa的数据（1GPa以下由于晶体场效应的影响无法从电阻准确估计T∗），虽然TK改变了近两个数量级，所得曲线仍然和公式（8）一致，支持特征温标T∗起源于RKKY相互作用，而非传统所认为的Kondo温度。

以上结果表明，f电子间的磁交换作用在Kondo晶格物理中发挥了关键作用，把局域的杂化效应传递到了整个晶格，导致了f电子与导带电子之间的非局域纠缠和集体响应。由此产生的重电子复合态不同于单杂质Kondo共振态在空间上的简单叠加，而是晶格自旋和导带电子集体协同的结果，包含了晶格自旋之间的关联效应，是一种全新的量子物态。

B.正常态物性

二流体理论可以定性或定量地解释重费米子正常态的一些反常现象，如：

1.磁化率低温下偏离居里–外斯定律；

2.核磁共振奈特位移低温下偏离对静态磁化率的线性关系；

3.自旋–晶格弛豫率随温度发生斜率的改变；

4.磁熵低温下被抑制；

5.电阻率温度曲线上的相干峰；

6.点接触谱的低温非对称线型（Fano线型）；

7.拉曼谱线型的低温变化。

这些现象在重费米子材料中具有普遍性，很早已经在实验上发现，但是一直缺乏比较系统的理论解释。比如电阻率温度曲线上的相干峰一般归结为晶格Kondo效应，而磁化率在相似温度处对居里–外斯定律的偏离则在文献中普遍被解释为由晶体场效应导致。

2008年，Yang等人[48]分析了近三十种重费米子材料的实验数据，发现这些反常现象均发生在共同的特征温标T∗处，因而应有共同的物理起源。在这一节中，我们将利用二流体理论对这些反常现象给出一个比较系统的解释。

1.磁性质

a.磁化率和奈特位移反常

在NMR实验中，带自旋的原子核的能级在外加磁场下会出现塞曼（Zeeman）劈裂，但是核自旋与周围极化电子的自旋之间的超精细耦合会使得能级出现额外的改变，即奈特位移。一般来说，金属中奈特位移K和电子的磁化率χ呈线性关系：K=K0+Aχ。其中A为与温度无关的超精细耦合常数，K0为常数项，通常起源于轨道的贡献[61]。但是在重费米子材料中，以图4所示的CeCoIn5为例[62]，这一线性关系只在高温时成立，当温度降到T∗以下时就发生了偏离。由于在重费米子材料中，对磁化率的主要贡献来源于f电子，导带电子的贡献可以忽略，文献中往往认为是晶体场效应引起的f电子的轨道分布随温度发生了变化，导致了这一反常偏离。

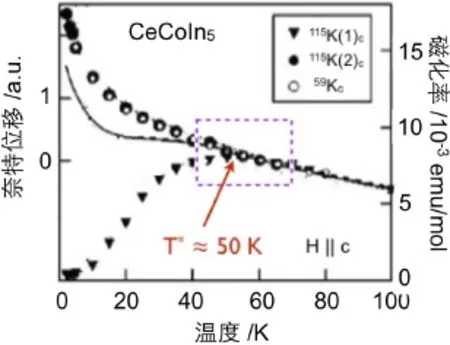
图4.CeCoIn5不同原子核上测量的奈特位移和磁化率（实线）的对比，在T∗≈50 K时二者偏离线性关系[62]

二流体理论对此给出了新的解释[46，47]：假设Kondo液体和自旋液体与原子核之间具有不同的超精细耦合常数A和B，则它们对磁化率χ和奈特位移K就会有不同的贡献∶

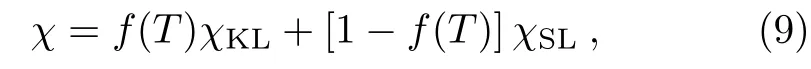
和

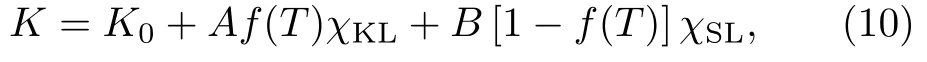
其中χKL和χSL分别表示Kondo液体和自旋液体的摩尔磁化率。在T∗以上，只有局域磁矩构成的自旋液体（导带电子的贡献为常数，且比较小可以忽略），f（T）=0，因此奈特位移与磁化率之间显示为线性关系K=K0+Bχ。而在T∗以下，Kondo液体出现，由于χKL̸=0，奈特位移与磁化率之间不再具有线性关系，出现反常：

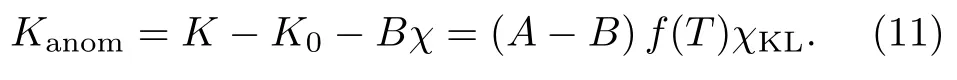
如果我们进一步假设Kondo液体贡献的总磁化率f（T）χKL正比于其态密度，则奈特位移反常具有如公式（6）所示的普适温度依赖行为。图5比较了十几种材料中奈特位移反常的实验数据[47]，我们惊奇地发现，奈特位移反常随温度变化的确呈现普适的演化关系，不依赖于材料的细节，在很大的温度区间内符合二流体理论的预言。这种不依赖于具体材料的晶格和电子结构的普适行为意味着奈特位移反常与晶体场效应无关，从而为二流体理论提供了重要的实验支持，同时表明巡游重电子的产生遵循某种与具体材料无关的普遍性的组织原则。

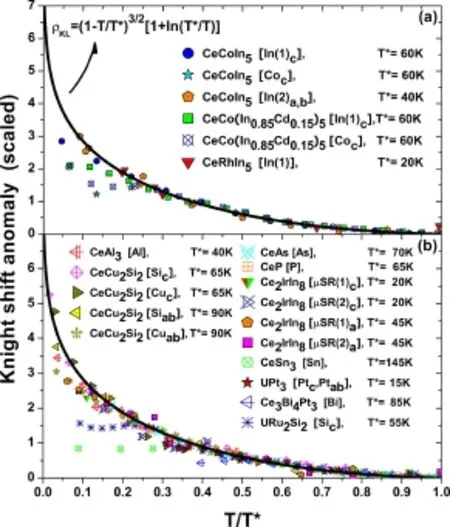
图5.一些重费米子材料中奈特位移反常随温度的演化[47]。实线为Kondo液体的态密度

b.自旋–晶格弛豫率

按照一般的Moriya公式[63]，NMR/NQR实验中的自旋–晶格弛豫率1/T1与动力学磁化率χ（q，ω）之间满足如下关系：

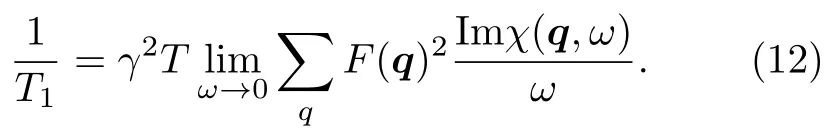
其中γ为原子核的旋磁比，F（q）为与晶格相关的结构因子。可以想象，两种流体的存在意味着自旋–晶格弛豫率也有两个来源，与巡游重电子和晶格自旋液体的耦合均会导致核自旋的弛豫[64]，

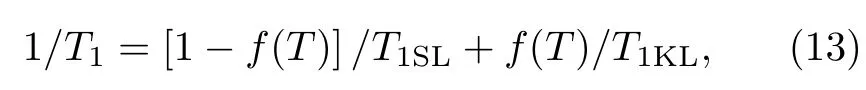
其中T1SL和T1KL分别对应晶格自旋液体和巡游重电子的本征贡献。图6给出了CeCoIn5的自旋–晶格弛豫率1/T1在不同压强下的测量结果[64]。实验发现，在很多重费米子材料中，T1在T∗之上都不随温度变化，意味着T1SL是与温度无关的常数。将这一结论推广到低温，利用以上公式对CeCoIn5的实验数据进行分析发现，T1KLT∼T+T0，其中T0为常数。这一结果类似于在铜氧化物超导中发现的二维反铁磁量子临界涨落的行为，其中T0表征系统偏离量子临界点的距离。图6中实线为采用上述公式拟合所得曲线，我们看到理论与实验观测结果吻合；点线是晶格自旋液体的贡献，低温下对实验值的偏离反映了重电子的贡献。

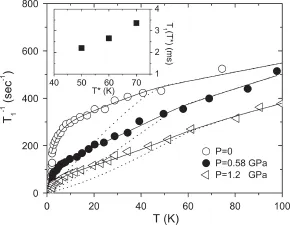
图6.CeCoIn5在不同压力下的自旋–晶格弛豫率随温度的变化[64]。实线为理论拟合，虚线为局域磁矩的贡献。插图给出了T1(T∗)随T∗的变化

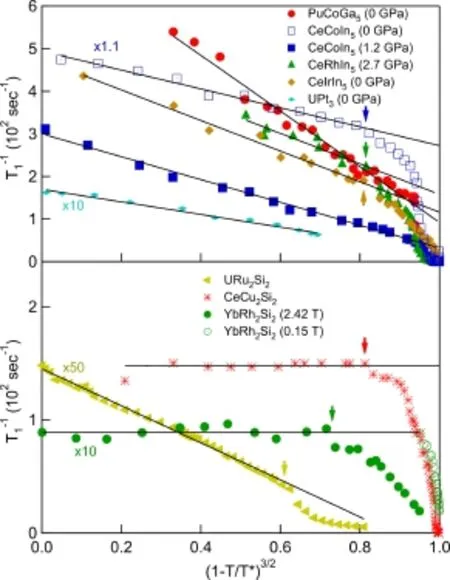
图7.一些重费米子材料的自旋–晶格弛豫率与(1− T/T∗)3/2的线性关系[65]。箭头表示对线性关系的偏离

在量子临界点附近，T0≈0，因而在很大的温度区间里（T≫T0），T1KL近似为常数。结合f（T）的公式，二流体理论预言1/T1也具有普适的温度演化[65]：

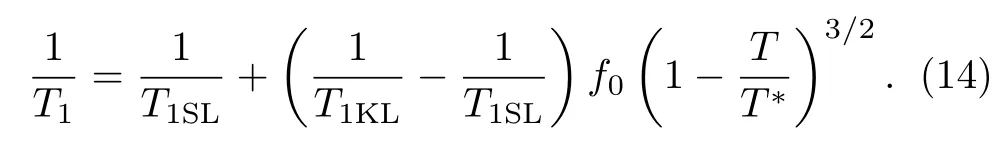
图7将几种材料在量子临界点附近的1/T1与（1−T/T∗）3/2对比[65]，发现这些材料在很大温度范围内的确满足以上公式预言的线性关系，进一步验证了自旋–晶格弛豫率的二流体公式。

2.热性质

温度高于T∗时，f电子完全局域化，假若基态为二重态，则磁熵接近饱和值Rln2（R为气体常数）。温度低于T∗时，部分f电子与导带电子集体杂化（纠缠），形成巡游重电子[49]。因而在二流体理论中，总磁熵应该是两种流体的贡献之和：

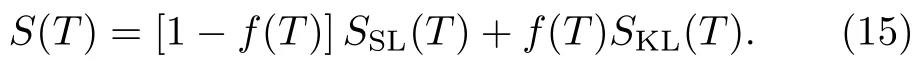
公式中SSL和SKL分别代表局域磁矩和巡游重电子的本征磁熵。对温度求导数得到比热系数，

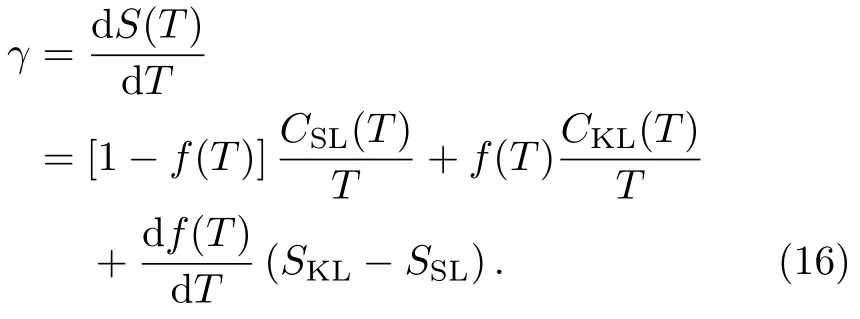
与公式（3）不同，此表达式中多出了f（T）的温度导数项，反映了两种流体的权重随温度变化的效应。公式中巡游重电子的比热系数满足普适的标度关系CKL/T∝[1+ln（T∗/T）]，对温度积分可得SKL（T）∝T[2+ln（T∗/T）]。假设f电子从局域磁矩到巡游重电子的转变是连续的，不存在熵变，则SKL（T∗）= SSL（T∗）=Rln2，可以得到T∗以下重电子的磁熵为[49]∶

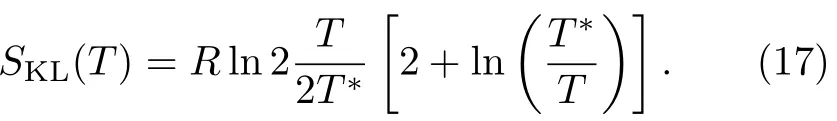
如果低温存在磁性等长程序，则Kondo液体的普适标度律不再成立，以上公式在低温下需要修正。同样若f电子完全退局域化，在低温下形成重费米液体，则比热系数中的对数发散会被截断，假设截断温度为TL，则f（T＜TL）=1，在此温度之下体系中只存在Kondo液体，总的低温比热系数可以近似估计为

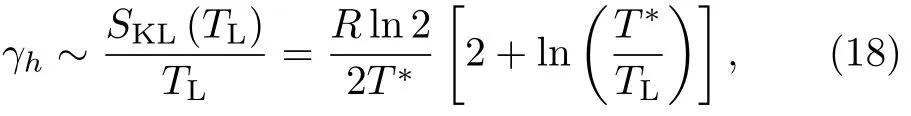
其中TL的具体数值可由实验确定（见III.C节）。一般情况下，必须要考虑到局域磁矩的贡献。如果我们取一个粗糙的近似，SSL（T）=Rln2，认为正常态下局域磁矩的内禀熵不随温度变化，则结合公式（16）可以计算出总的比热系数。图8对比了几种重费米子材料的低温比热系数的实验测量结果与理论预言值，两者之间总体上符合[49]。

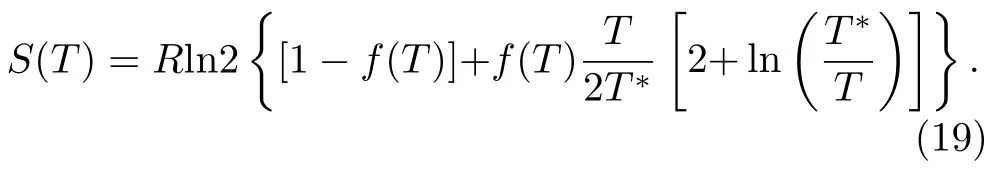
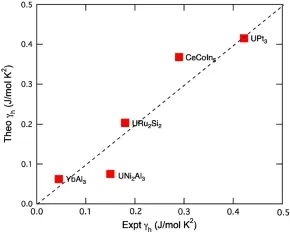
图8.几种重费米子材料的比热系数的理论与实验对比[49]

3.电输运性质

(1)霍尔系数

重费米子材料的霍尔系数具有非常复杂的温度依赖行为，长期以来缺乏系统的理论解释。1987年，Fert和Levy提出晶格上局域自旋会对导带电子产生斜散射（skew scattering）[66]，导致霍尔系数出现反常温度依赖：Rs=rlρχ，其中rl是常数，ρ为纵向电阻，χ是磁化率。总的霍尔系数为：RH=R0+Rs，其中R0来源于导带电子的正常贡献。Fert和Levy的理论很好地解释了霍尔系数在高温区的温度变化，但是却无法解释T∗以下的行为。

2004年，Hundley等人发现CeMIn5（M=Co，Rh，Ir）系列材料的霍尔系数在高温几乎不随温度变化，意味着斜散射的效应可以忽略，即rl≈0，但是在低温下却出现反常增大[67]。2008年，Yang和Pines分析了他们的数据[48]，发现霍尔系数的反常增加恰好出现在相干温度T∗以下，并且其温度依赖行为与二流体理论预言的重电子普适标度律一致，如图9所示[49]，表明Kondo液体对霍尔系数的贡献不遵循Fert和Levy提出的斜散射规律，而是与电阻无关，只与Kondo液体的磁化率成正比。2009年，Yang由此提出重费米子霍尔系数的二流体公式[68]：

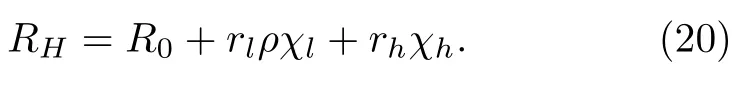
公式右边的rlρχl和rhχh两项分别是局域磁矩和重电子的贡献，具有不同的规律，其中χl=[1−f（T）]χSL和χh=f（T）χKL为两种流体各自对磁化率的贡献，实验上可以通过对奈特位移与磁化率的联合分析确定。高温时只有f局域磁矩，因而霍尔系数与磁化率和电阻的乘积成线性关系，，回归到Fert和Levy的斜散射公式；而在T∗以下的相干区，新出现的巡游重电子的不同贡献，导致了对Fert和Levy的公式的偏离。图10给出了对URu2Si2的实验数据的理论拟合[68]，公式中的R0和rl可以通过高温（T＞T∗）拟合得到，因而低温下只有一个自由参数rh，但在18.5 K低温隐藏序出现以上的整个温度区间内都给出了与实验定量符合的结果。

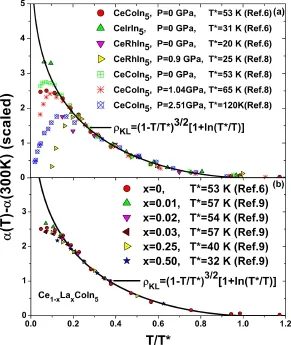
图9.CeMIn5和Ce1−xLaxCoIn5的霍尔系数随温度变化的标度行为[49]

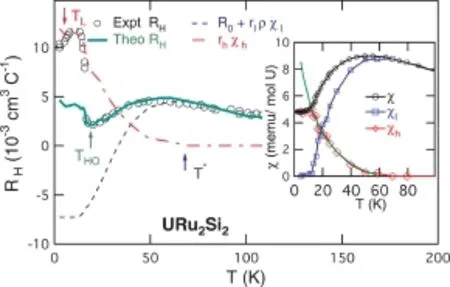
图10.URu2Si2霍尔系数随温度的变化[68]。实线为理论拟合，虚线代表Kondo液体和局域磁矩斜散射的贡献。插图中χ、χl、χh对应总磁化率和二流体分析给出的局域磁矩及重电子对磁化率的贡献

可以看到，两种流体对霍尔系数的贡献具有非常不同的温度依赖性，因而总的霍尔系数表现出复杂的温度依赖行为，缺乏简单的规律性，阻碍了理论认识的发展。在CeMIn5系列材料中，局域磁矩的贡献由于未知的原因被抑制，重电子Kondo液体的贡献才显现出来，展现出简单的标度行为，使得对霍尔系数的进一步分析成为可能。

(2)Fano干涉效应

在点接触谱（PCS）和扫描隧道谱（STS）中，微分电导dI/dV可以反映出体系中的集体激发和载流子的态密度等重要性质。对重费米子材料的PCS的实验研究已经有三十年的历史[69]，STS的研究在最近几年也有突破性的实验进展[70∼72]，都发现电导谱在低温下普遍呈现非对称的线型（如CeCu6[73]，CeCoIn5[74，75]等）。

2009年，Yang基于导带电子和f电子的杂化图像在理论上预言了重电子的Fano干涉效应[76]：低温下，重费米子体系中的导带电子与f电子局域磁矩集体杂化，使得f电子产生退局域化，从而探针中的电子可以通过两个通道进入重费米子材料，或直接隧穿到导带，或隧穿到晶格上的f能带。如图11所示，类似于光的双缝干涉效应，入射电子在这两个通道之间也会发生干涉[77]。

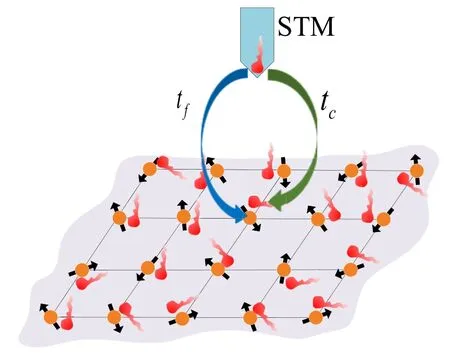
图11.重费米子Fano干涉效应示意图。tf和tc分别表示扫描隧道显微镜（STM）探针中的电子进入f能带和导带两个不同通道的隧穿系数

理论上，低温下导带电子与f电子之间发生集体杂化，将f电子的能级重整化到了费米能级附近，在隶玻色子方法近似下，体系的低能有效哈密顿量可以写为

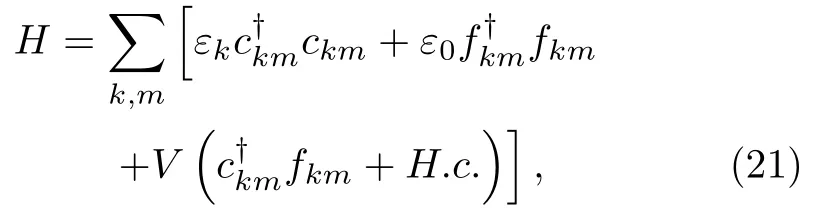
其中ckm和fkm是第m个轨道（自旋）上的导带电子和f电子的湮灭算符，ε0和V是重整化后的f能级及其与导带电子的杂化强度。假设金属探针与样品间的耦合可通过以下哈密顿量来描述，

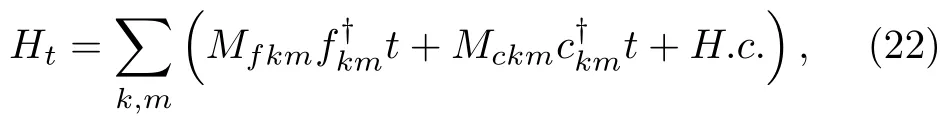
其中t是探针上电子的湮灭算符，M是隧穿矩阵，简单计算可得体系的微分电导为

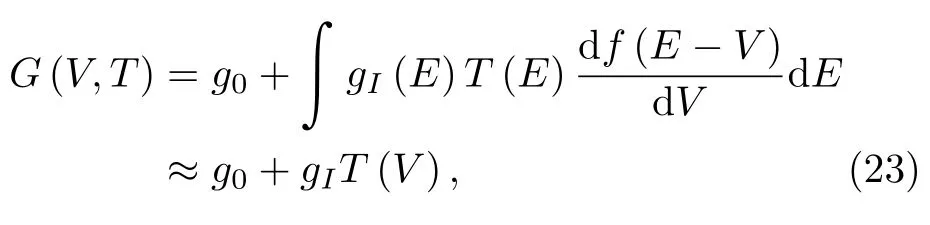
其中f（E）是费米分布函数，g0为背景电导，T（E）具有Fano线型

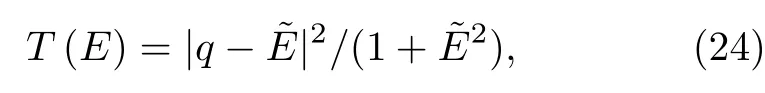
其中参数q=Mfkm/Mckm代表探针与两个不同通道间的有效耦合强度的比率，=（E−ε0）/V，gI（E）是一个与能量有关的系数：

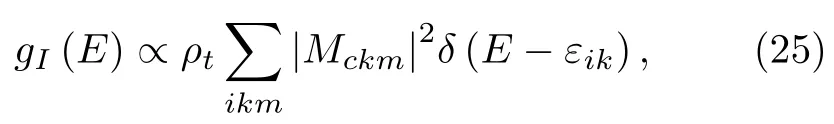
其中ρt为金属探针的态密度，εik为第i个杂化能带。在STS实验中，由于空间上的局域性，每个k点的隧穿几率相同，Mckm无动量依赖性，所以gI（E）正比于态密度，从而可以明显地看出导带与f能带之间的杂化能隙。而在PCS实验中，不同的k点具有不同的隧穿几率，gI（E）是动量空间的加权平均，具有比较复杂的形式，不能简单地反映态密度的信息，再加上热或关联效应，电导曲线上的能隙往往被抹平。假设gI（E）是常数，则如图12所示[62]，在q=0或∞的极限下，探针只与导带或f电子单独耦合，微分电导dI/dV曲线在零偏压处出现共振峰或谷；而对一般的q，两个通道之间存在干涉，会导致特定偏压下电导被抑制，出现典型的非对称Fano线型。

图13给出了对CeCoIn5的PCS实验数据的理论拟合，在考虑了偏压和温度对平均场参数的影响后，利用Fano线型公式很好地解释了PCS随温度和偏压的变化[76]。在一些材料中，电导曲线在很高温度时已经显现出非对称性，这可能是由于导带电子态密度的非对称性或晶体场效应导致。对YbAl3和CeRhIn5等材料的实验分析表明[48]，非对称性在T∗之下伴随重电子的出现才变得更为显著。Fano效应揭示了巡游重电子作为复合粒子的物理本质，与二流体的理论预期一致。

在Yang的工作之后，有更多的理论[78，79]和实验[72，80∼82]都证实了重费米子材料中的Fano干涉现象，特别是在URu2Si2隐藏序[83]和SmB6表面态[84，85]的研究中也发现了Fano线型，为理解两种复杂现象的物理机理提供了重要信息。

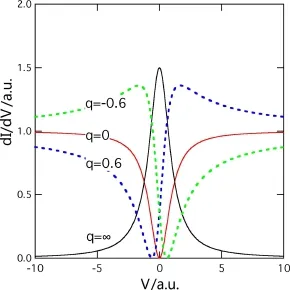
图12.微分电导随偏压的Fano曲线示意图[62]，q是Fano参数

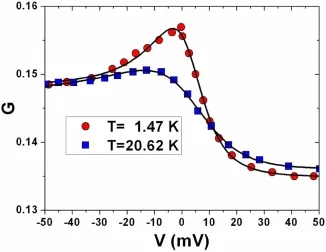
图13.CeCoIn5在不同温度下的点接触电导谱的理论拟合（实线）[76]

C.低温有序态

二流体图像成功描述了重费米子材料正常态的物理性质，解释了许多令人困惑的实验现象。2012年，Yang和Pines考虑到两种流体在低温下的不稳定性，将体系低温下磁或超导等基态长程序与二种流体在正常态的温度演化联系起来[49，86]，提出了新的二流体理论框架，更加全面地描述了重费米子物理。

图14给出了二流体理论预言的普适相图[49]：在特征温度T∗以下广阔的温度区间和压强范围内同时存在着重电子Kondo液体和局域自旋液体，两种流体既共存又竞争，在低温下由于各自磁或电的不稳定性而形成各种不同的有序态，如自旋液体可以产生局域的磁性序，Kondo液体可以形成超导、巡游磁性序或费米液体态等等。在二流体理论框架下，杂化效率f0是调节基态的重要参量，受到外界压力或磁场的调控。f0的大小决定了f电子巡游或局域部分的权重：

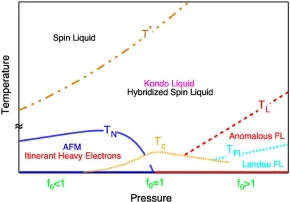
图14.二流体理论预言的重费米子相图[49]

1.当f0＞1时，杂化较强，所有f电子在一定温度TL之下都转化为巡游重电子，在更低温度时形成费米液体或超导。TL即为退局域化温度，满足f（TL）=1，其大小与f0相关。

2.当f0＜1时，杂化较弱，f（T）在零温时也小于1，因而低温下一直存在由未杂化的f电子形成的局域磁矩。这些剩余磁矩受RKKY交换作用的影响，在有限温度TN下会形成局域的磁长程序。实验表明，在反铁磁相变附近部分巡游重电子可能会发生重新局域化[87，88]，未重新局域化的巡游重电子在更低温度下有可能形成超导，导致超导与反铁磁共存。

3.f0=1时，f电子在零温处完全退局域化，体系处于量子临界点附近，强烈的量子临界涨落可能会诱导巡游重电子发生超导配对。

杂化效率f0的大小也会影响到正常态，因而在二流体理论中，低温基态与高温正常态的行为之间存在密切关系。下面我们将结合图14，从费米液体、磁有序态、量子临界行为、超导四个方面介绍二流体理论对重费米子低温有序态的理解。

1.费米液体

如上所述，f（TL）=1定义了退局域化温度TL，

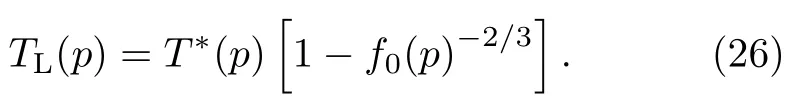
在TL之下所有的f电子都从局域磁矩转变为了巡游重电子[49]。上式要求f0≥1：当f0=1时，TL=0，实验表明此处费米面会发生突变[89]；而当f0＞1时，TL＞0，费米面的变化是渐进的，在TL附近存在很强的涨落，巡游重电子受到强烈的散射，导致在TL附近表现为反常的费米液体行为，引起一系列的反常现象，如电阻系数出现峰值（如CeCoIn5[90]），霍尔系数发生较大的变化（如YbRh2Si2[91]）等等。在更低温度TFL下，才开始出现定义良好的准粒子，表现出传统的朗道费米液体行为，即电阻呈现T2的依赖关系。在此费米液体区，二流体理论有一些定量的预言。图8对比了一些材料中的低温比热系数，理论预期与实验结果基本一致[49]。

2.磁有序态

在平均场近似下，局域自旋液体的磁化率可以用公式（7）来描述。当f0＜1时，fl（0）=0，零温下剩余未杂化的局域磁矩可以形成磁有序态，转变温度TN满足：

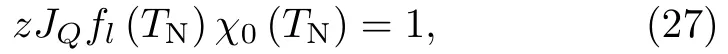
即，

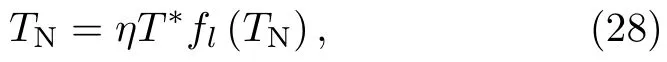
其中Q为磁性长程序的波矢，参数η=CzJQ/T∗反映了阻挫对TN的影响，fl（TN）=1−f（TN）则反映了集体杂化对TN的抑制。二流体理论进一步预言，f电子在形成磁性序时的有效局域磁矩被削减为，

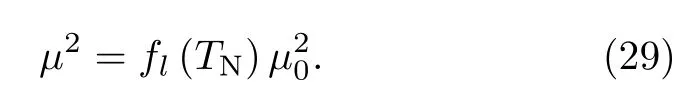
结合两式得到，

以CeRhIn5为例，随着外加压力的增加，T∗升高，而µ变小，因此TN（p）有一个极大值，如图14所示[49]。图15给出了CeRhIn5的TN和有效磁矩等随压力变化的实验结果[49]，实线或虚线为理论拟合，二者基本符合。

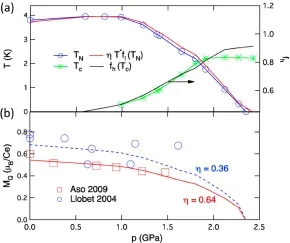
图15.CeRhIn5的Nel温度TN和有效磁矩[92，93]的理论拟合（线）[49]

3.量子临界行为

在量子临界区，体系的低能激发不仅仅包含了磁性序参量的涨落，也包含了费米子自由度的低能激发，呈现出复杂的反常量子临界现象，电阻、磁化率、比热等物理量也随温度出现非常规的标度行为[94，95]，迄今仍缺乏比较系统的理论解释。二流体理论包含局域自旋的磁性涨落和费米面附近的巡游重电子，可以同时处理两种自由度及其相互作用，有可能为理解重费米子材料中的反常量子临界现象提供新的思路。在这一节中，我们简要介绍一些相关的研究进展，主要是量子临界点在磁场和外加压力下的移动，以及部分物理量的标度行为。

我们首先讨论量子临界点在磁场和外加压力下的移动。在一些重费米子材料如CeCoIn5和YbRh2Si2中，实验表明[90，96，97]反铁磁量子临界点会随外加磁场改变，即临界压力pc是磁场的函数，从而在p−H相图上形成一条量子临界线，如图16（a）和图17（a）所示[98]。在二流体理论中，局域磁性序的量子临界点由方程f0（p，H）=1决定，此处退局域化温度TL=0，f电子的局域性完全被抑制，局域反铁磁序消失。对压力和磁场作微扰展开，假设[98]

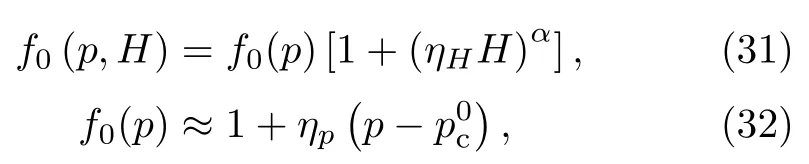
则量子临界点的位置满足：

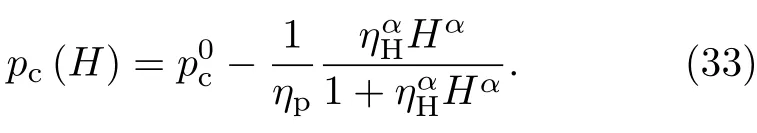
图16（a）和图17（a）给出了对CeCoIn5和YbRh2Si2的量子临界线的理论拟合[98]，发现对CeCoIn5，α=2；而对YbRh2Si2，α=0.8。不同的α值表明两种材料具有非常不同的量子临界行为。

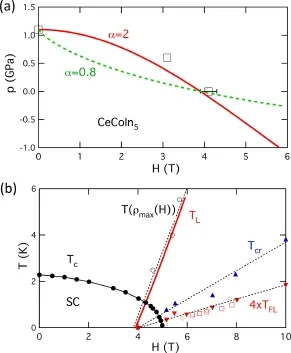
图16.(a)CeCoIn5的p−H相图和对量子临界线的理论拟合（实线）；(b)CeCoIn5的T−H相图和对退局域化温度TL(H)的理论拟合（实线）[98]

在有限温度下，固定外界压力，可以得到退局域化温度TL随磁场的变化，即

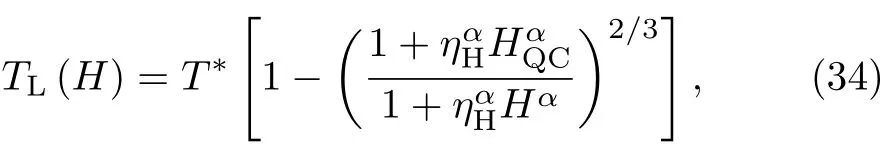
Yang和Pines进一步发现，量子临界点附近电子的有效质量和比热系数随磁场满足如下标度行为：

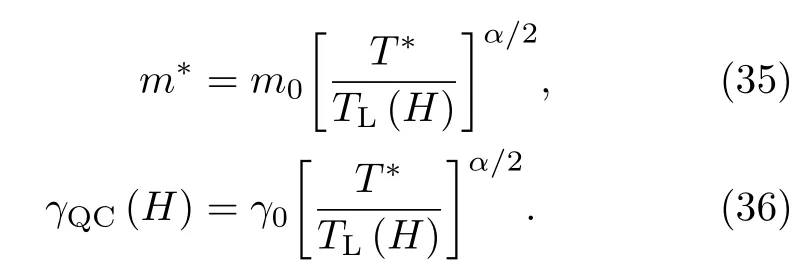
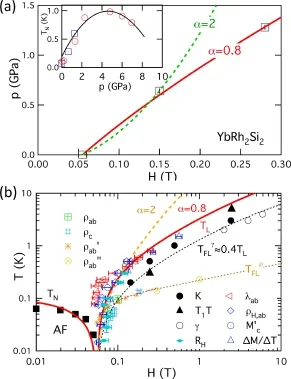
图17.(a)YbRh2Si2的p−H相图和对量子临界线的理论拟合（实线），插图为对反铁磁转变温度TN(p)的理论拟合（实线）；(b)YbRh2Si2的T−H相图和对退局域化温度TL(H)及TN(H)的理论拟合（实线）[98]

如果取Kadowaki-Woods比率A（H）/γ（H）2为常数（其中A（H）为电阻系数：ρ（H，T）=ρ0+A（H）T2），则有

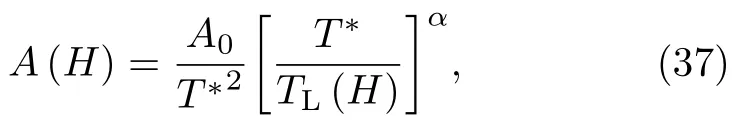
其中A0是与磁场无关的系数。图18给出了对YbRh2Si2的电阻系数的理论拟合[98]，验证了以上公式。

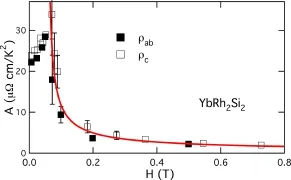
图18.YbRh2Si2的电阻系数随磁场变化的实验与理论（实线）比较[98]

以上结果进一步验证了二流体理论。目前实验认为，CeCoIn5中的量子临界点为自旋密度波（SDW）类型[100]，而YbRh2Si2则呈现非常规的局域量子临界行为[101]。这两类不同的量子临界行为体现在特征参数α的不同取值上，其物理意义有待更深入的研究。

4.超导

在量子临界点附近，局域反铁磁序被抑制，其低能量子临界自旋涨落可能诱导巡游重电子产生超导配对[102]。NMR实验揭示了重电子的量子临界自旋涨落在超导凝聚中发挥的关键作用。

以CeCoIn5为例，二流体分析发现[64]，NMR奈特位移反常在超导温度Tc之上具有普适的Kondo液体标度行为，不依赖于实验中所测量的原子核，反映了重电子的本征温度演化；而在Tc之下，则出现BCS理论预言的d波超导的典型行为，表明低温超导相确实是重电子Kondo液体的凝聚。理论拟合得到的超导能隙∆（0）/Tc∼4.5及比热跃变∆C/C∼4，均和其他实验符合[100，103]。同时，利用公式（14）对自旋–晶格弛豫率的分析也发现，重电子的自旋–晶格弛豫率1/T1KL在T∗之下满足[53，64]

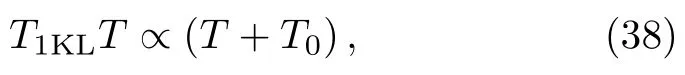
类似于铜基超导中的准二维磁性量子临界涨落，揭示了CeCoIn5中重电子的隐藏的磁性量子临界行为。我们认为这是导致重电子超导配对的微观根源。这一结果与最近基于STM、NMR和中子散射实验进行的理论分析一致[104]。

在此基础上，Yang和Pines推广了早期铜氧化物高温超导中自旋涨落诱导超导配对的图像，并结合二流体理论，提出重费米子超导转变温度Tc满足[86]：

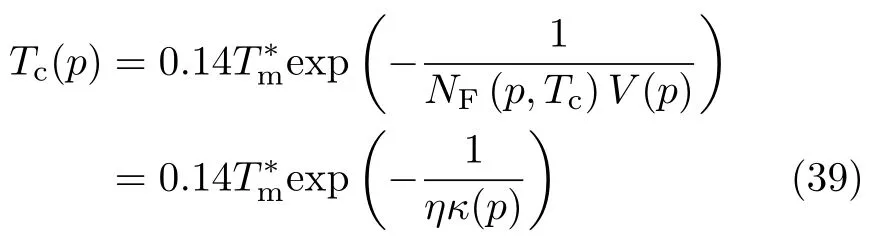
其中κ（p）=NF（p，Tc）T∗是无量纲的态密度，η（p）=V（p）/T∗反映了准粒子与自旋涨落之间的耦合强度。为超导峰值处的特征相干温度，代表了自旋涨落的特征能量，类似于BCS理论中的Debye频率。引入是由于实验上发现重费米子材料的最高Tc与之间存在标度关系[86，105]。

以上公式中，由于态密度随温度降低呈对数发散，其截断温度直接影响了Tc的大小。分析表明，超导相随外加压力呈现穹顶（dome）结构，并且如图19所示，可以划分为三个区域[86]：

1.当p＞pL时，超导相之上为费米液体。截断温度TL（p）随着压力增加而变大，低温下重电子的态密度随之降低，导致Tc随压力的增加而下降。

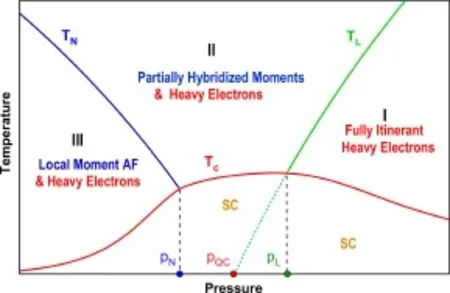
图19.二流体理论预言的重费米子超导相图[86]。在区域I中，TL以下局域磁矩与导带电子完全杂化，只有巡游重电子存在；在区域II中，集体杂化不完全，巡游重电子和剩余的局域磁矩共存；在区域III中，TN以下剩余的局域磁矩形成反铁磁序，同时仍然存在着重电子。在Tc以下，量子临界涨落诱导重电子配对形成超导(SC)

2.当p＜pN时，截断温度为TN（p）或T0（p），f电子随压力减小趋向局域化，重电子权重减少，态密度减小，Tc也随之降低。在此区域中，由于同时存在局域和巡游的f电子，可能出现局域反铁磁序与超导相共存。

3.在量子临界点附近，截断温度为Tc（p）自身，超导转变温度必须通过公式（39）自洽求解。

上述公式定量预言了Tc对压力的依赖行为，并且由于κ（p）在实验上可以通过比热测量估计，η（p）与压力近似无关，可以由超导转变温度的最大值估计，因而公式中没有多余的自由参数。图20给出了对CeCoIn5和CeRhIn5的理论拟合[86]，与实验定量相符。这又一次验证了二流体理论的有效性，同时表明在二流体理论框架下，将量子临界涨落与准粒子的重整化两种强关联效应分开作简化近似处理是可行的，抓住了重费米子超导的本质物理。

IV.实验进展

重费米子二流体理论不但解释了众多先前的实验结果，也得到了一些新实验的支持，本章将介绍几个典型的实验进展。

A.角分辨光电子能谱

角分辨光电子能谱（ARPES）提供了重电子温度演化的直接信息。2012年，沈志勋组利用ARPES对YbRh2Si2中重电子态的温度演化进行了细致的测量和分析[106]，发现在T∗=50±10 K以下重电子态开始出现并随温度降低逐渐增强，与二流体理论的预言一致。图21给出了他们的实验结果[106]。可以看到，在45 K以下，费米能附近逐渐出现了一个新的准粒子峰，对应于新形成的巡游f电子，其谱权重在T∗以下随温度降低逐渐增强。

目前，理论上对重电子及其费米面的温度演化尚存在不同认识，利用ARPES测量实际重费米子材料中的费米面演化是一个重要的前沿课题。

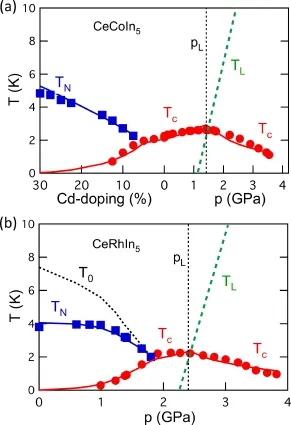
图20.CeCoIn5和CeRhIn5的p−T相图[86]。实线为二流体理论的拟合

B.缪介子自旋共振

2009年，Ohishi等人借助缪介子自旋共振（µSR）对重费米子材料（Ce1−xLax）2IrIn8进行了系统的测量[107]。他们发现在所有的样品中，缪介子奈特位移在一定温度下都会偏离与磁化率的线性关系。他们排除了晶体场效应的影响，得到了类似于核磁共振奈特位移反常的现象。图22给出了x≤0.5时的实验结果[107]，µSR奈特位移反常完全符合公式（6）给出的Kondo液体普适标度律，为二流体理论提供了有力支持。

此外，对CeIrIn5[108]、CePt2In7[109]、U2Pt2Sn[110]等材料的最新研究，以及一些光电导、STM等新的实验也都验证了二流体理论的预言。

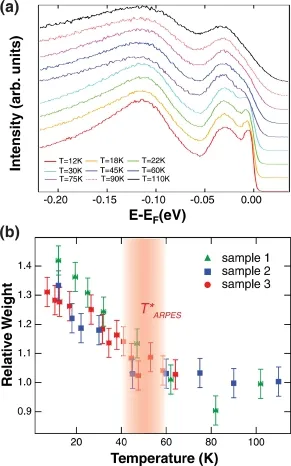
图21.YbRh2Si2的角分辨光电子谱[106]。(a)温度小于45 K时，在费米能附近出现准粒子峰；(b)温度低于T∗ARPES时，准粒子谱权重随温度降低逐渐增强

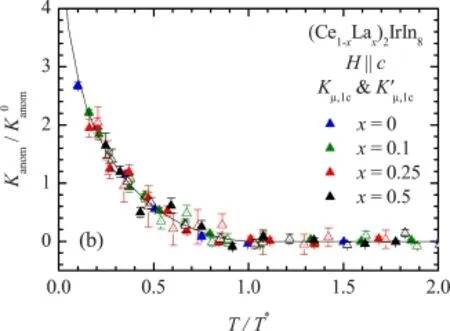
图22.(Ce1−xLax)2IrIn8奈特位移反常的标度行为[107]，实线为二流体理论的预言

C.新材料

二流体理论的预言在一些新发现的重费米子材料中也得到了验证。此处我们简要介绍一种新型的d电子重费米子化合物，CaCu3Ir4O12，为中国科学院物理研究所的程金光等人最近采用高压方法合成的钙钛矿材料[5]。

如图23（a）和（b）所示[5]，实验发现此材料在温度为80 K时呈现出一系列的反常现象：磁化率开始偏离高温的居里–外斯定律，电阻偏离了与温度的线性关系等。这些反常现象与二流体理论预言的重费米子特征行为非常类似，特别是低温下，比热系数对温度呈现对数依赖［图23（c）］，并且磁化率在T∗=80 K附近出现平台。能带计算发现，Cu2+上只有一个空穴，占据了较窄的dxy能带，存在很强的局域库仑相互作用，并且与周围Ir上较为巡游的d电子能带杂化。这些研究表明CaCu3Ir4O12与常规的f电子重费米子材料类似，是一种少见的d电子重费米子材料。

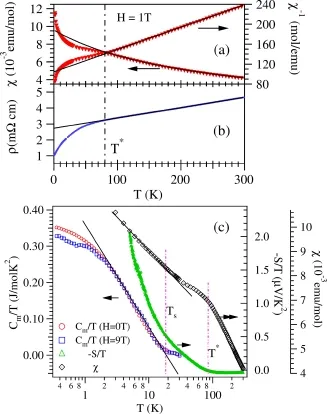
图23.CaCu3Ir4O12磁化率χ(T)、电阻ρ(T)、磁性比热Cm(T)等随温度的变化[5]

类似的行为在新近合成的LaCu3Ir4O12材料中也被发现，同样符合二流体理论的预言，其特征温度T∗为150 K[111]。二流体理论所揭示的重费米子物理的本质特征引导了新型重费米子材料的实验探索。

V.理论进展

二流体唯象理论获得了极大的成功，理解其背后的微观机理是目前面临的首要理论问题。在这一章中，我们简要介绍相关的理论探索，包括采用隶玻色子近似、单杂质动力学平均场理论（DMFT）、数值重整化群（NRG）、行列式量子蒙特卡罗（DQMC）和密度矩阵重整化群（DMRG）等方法进行的研究工作。

A.隶玻色子近似

2006年，Barzykin利用隶玻色子近似在大N极限下计算了周期性Anderson模型的比热和磁化率，考虑到费米面附近较为平坦的杂化能带的贡献，可以将这两个量写作两分量的形式，从而得到了一个权重函数[112]：

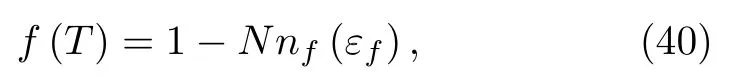
其中nf（εf）是巡游f电子的占据数，f（T）代表了二流体理论中局域部分的权重。这一结果虽然定量上与二流体理论的唯象预言不符，并且还忽略了f电子间很强的RKKY交换关联效应，但物理图像简单清晰，值得进一步研究。二流体理论的微观描述的建立，最终可能需要引入新的平均场近似方案。

B.单杂质DMFT

2007年，Kotliar小组利用单杂质DMFT结合第一性原理方法，首次对CeIrIn5的4f电子能谱进行了细致的计算分析[35]。他们发现f电子在室温时紧密地束缚在Ce离子周围，表现出完全的局域性，其谱权重主要聚集在能量−2.5 eV和3 eV附近，在费米面处几乎为零。直到50 K以下，f电子的态密度才随着温度降低快速增加，在费米面处逐渐形成一个尖锐的准粒子峰，呈现出巡游的性质。Yang和Pines发现此准粒子峰的高度随温度的变化与二流体理论预言的Kondo液体态密度的温度演化行为一致（图24）[47]，后来的计算更进一步地验证了这一结果[113]。单杂质DMFT虽然也不包含f电子间的反铁磁关联，但是其计算结果与二流体预言一致的背后应有更深刻的物理根源，有待更加细致深入的分析。

C.NRG

2011年，Jian-Xin Zhu小组利用NRG方法研究了两杂质Anderson模型[114]。如图25所示[114]，他们发现体系中存在两个基本的温标：高温温标TH对应于准粒子的形成，低温温标TL对应于准粒子开始表现出费米液体行为。在二流体理论中，这两个温标分别对应T∗和TFL。他们发现，在很大的参数区间内，TH源自两杂质体系从自旋单态到自旋三重态的激发，此时TH≫TL，RKKY相互作用占主导，但是低温下仍然形成重电子，与二流体理论的预期一致；只在很强杂化时，TH才趋近单杂质的Kondo温度，此时TH∼TL。他们同时发现，RKKY作用在高温时会促进重电子的形成，符合二流体理论的预期，而不是如Doniach相图所示简单地抑制费米液体。这为理解T∗的微观起源和RKKY作用的物理提供了新的认识。

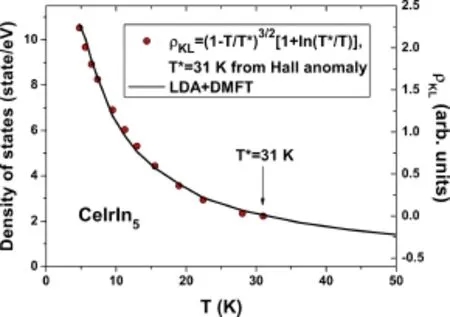
图24.LDA+DMFT计算得到的CeIrIn5准粒子峰态密度(实线)与Kondo液体态密度的比较[47]

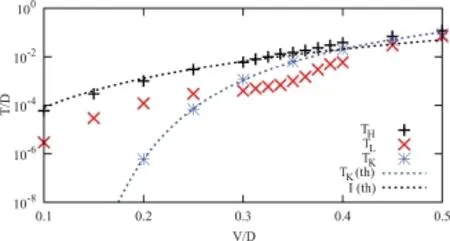
图25.NRG计算中得到的各个能标随杂化强度V的变化[114]，虚线为理论拟合值

D.DQMC

2014年，Scalettar小组利用DQMC计算了二维半满周期性Anderson模型的磁化率和奈特位移[115]。图26给出了他们得到的奈特位移反常随温度的变化，虚线为二流体理论的预言[115]，可以看到两者在特征温标T∗之下很大的温度区间内近似符合。目前这一工作只考虑了f电子半满的情况，此时体系为绝缘体，DQMC计算中没有符号问题。为了研究巡游重电子的演化，有待将其推广到更一般的偏离半满的情况。

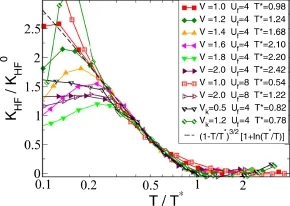
图26.DQMC计算给出的奈特位移反常与Kondo液体态密度（虚线）的比较[115]

E.DMRG

最近，我们利用密度矩阵重整化群（DMRG）方法研究了一维Kondo-Heisenberg模型，通过分析局域自旋从局域到巡游的转变过程，探讨f电子局域和巡游二重性的微观根源[116]。

在Kondo-Heisenberg模型中，局域自旋的关联谱在动量空间的积分是个与Kondo耦合无关的常量，因而局域自旋的状态的改变体现为自旋关联谱在动量空间的分布的变化。如图27（a）所示[116]，我们发现随着JK的增加，这一分布逐渐从k=π处尖锐的峰状结构转变为在整个空间比较均匀的分布，反映了局域自旋从强的链内Heisenberg耦合到强的局域近藤耦合的转变。这一转变同时伴随着导带电子在动量空间从小费米面到大费米面的过渡［图27（b）］，意味着费米面的变化与链内反铁磁关联的抑制是一致的，与实验发现的反铁磁量子临界点处费米面的突然变化符合。此外，在强JK极限下，局域自旋的自旋关联谱在比较均匀的背景上出现一个新的峰，对应大费米面的特征波矢，表明局域自旋参与了大费米面的形成。这种巡游性源自局域自旋涨落与导带电子的耦合，意味着巡游重电子是一种复合粒子。更有意思的是，在中间JK区（JK/t=2.3附近），关联谱上出现多峰结构，分别对应链内反铁磁关联及大小费米面两种费米波矢［图27（a）］，这就表明局域自旋不但与链内其他自旋发生关联，也同时与导带电子发生纠缠，参与到大费米面的形成中，表现出局域和巡游的二重性质，如图27（c）所示。据此，我们提出局域自旋关联谱在动量空间的谱权重的转移可以作为反映其局域和巡游性质的序参量，为二流体理论中的杂化参量提供了一个微观的描述。

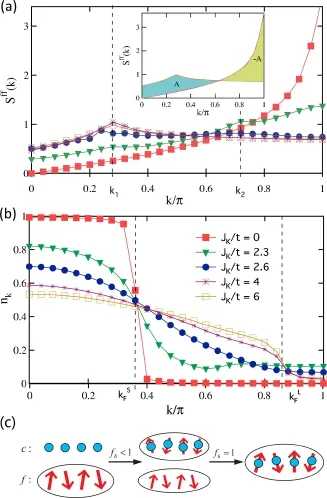
图27.DMRG给出的自旋关联谱和粒子占据数的计算结果。(a)f电子的动量空间自旋关联谱随JK的演化，k1和k2对应大费米面和小费米面的散射峰；插图中面积A表示JK=0和强耦合极限对比下的谱权重转移；(b)导带电子在动量空间的分布随JK的演化，其中对应小费米面，对应大费米面；(c)一维Kondo-Heisenberg模型二流体行为示意图。箭头表示f电子局域磁矩，圆点表示自由的导带电子。在不完全杂化时(fh＜1)，f电子部分和导带电子纠缠在一起，部分仍然保持磁矩，表现出巡游和局域的二重性；完全杂化时(fh=1)，f电子磁矩全部被导带电子屏蔽，表现出完全的巡游性[116]

以上结论虽然是基于一维Kondo-Heisenberg模型，但是局域自旋的纠缠性质并不局限于一维系统，类似的结论在二维或三维真实体系应该仍然成立。如何将以上结果推广到高维系统，并从中提炼出反映f电子局域或巡游性的“本征序参量”，是我们下一阶段研究的主要目标。

VI.结论和展望

综上所述，二流体理论为认识重费米子物理提供了一个简单的物理图像。在f电子局域和巡游二重性的基础上，通过引入两种共存流体的简单假设，二流体理论系统解释了大量先前无法解释的实验观测结果，发现了正常态的巡游重电子普适标度律和Fano干涉效应，建立了描述体系各种低温有序态的简单模型。二流体理论所预言的普适标度律表明f电子的演化规律是与具体材料的细节无关的物理行为，重电子态是一种新的量子物态。

与通常基于Kondo物理的方案不同，二流体理论更多地强调局域磁矩之间反铁磁耦合的作用，认为重费米子物理是导带电子与背景自旋晶格反铁磁涨落发生集体杂化或纠缠的结果，理解晶格自旋涨落在电子演化或费米面的变化中所发挥的作用应是发展重费米子理论的核心问题。

二流体理论目前仍然是一个基于实验的唯象理论。在微观层面上，两种流体如何共存，如何产生不稳定性，如何导致不同的量子临界现象，以及如何引起重电子的超导配对等等，都是需要继续深入研究的课题。实验上，利用中子散射等测量技术直接观测电子局域和巡游的二重属性，或借助STM和ARPES等手段在实空间或动量空间观测重电子态的产生和演化，将会为微观理论的发展提供重要的指引。

局域和巡游二重性是强关联电子系统的普遍现象，不仅出现在重费米子体系，也同样存在于其他的强关联电子系统如铜基和铁基超导中。这种局域和巡游的二重性体现了电子动能与其局域库仑排斥势的竞争，表明两者处于近似均衡的中间状态，无法利用单纯的局域或巡游的简单极限进行描述。重费米子二流体理论的成功表明在这种局域和巡游二重性的新的概念基础上，有可能为理解强关联电子的复杂行为构建简单的理论框架。

感谢国家重点基础研究发展计划（批准号：2015CB921303）、国家自然科学基金（批准号：11174339）、中国科学院B类战略性先导科技专项（批准号：XDB07020200）和“百人计划”项目的支持。

参考文献

[1]Coleman P.Ann.Henri.Poincar，2003，4：Suppl.2，S559-S580

[2]Stewart G R.Rev.Mod.Phys.，1984，56(4)：755-787

[3]Misra P.Heavy-Fermion Systems，New York.Elsevier，2008

[4]Kondo S，Johnston D C，Swenson C A，Borsa F，Mahajan A V，Miller L L，Gu T，Goldman A I，Maple M B，Gajewski D A，Freeman E J，Dilley N R，Dickey R P，Merrin J，Kojima K，Luke G M，Uemura Y J，Chmaissem O，Jorgensen J D.Phys.Rev.Lett.，1997，78(19)：3729-3732

[5]Cheng J G，Zhou J S，Yang Y F，Zhou H D，Matsubayashi K，Uwatoko Y，MacDonald A，Goodenough JB.Phys.Rev.Lett.，2013，111(17)：176403

[6]Yuan H Q，Grosche F M，Deppe M，Geibel C，Sparn G，Steglich F.Science，2003，302(12)：2104-2107

[7]Kenzelmann M，Gerber S，Egetenmeyer N，Gavilano J L，Strssle T，Bianchi A D，Ressouche E，Movshovich R，Bauer E D，Sarrao J L，Thompson J D.Phys.Rev. Lett.，2010，104(12)：127001-127004

[8]Mydosh J A，Oppeneer P M.Rev.Mod.Phys.，2011，83(4)：1301-1322

[9]Dzero M，Sun K，Galitski V，Coleman P.Phys.Rev. Lett.，2010，104(10)：106408

[10]Lu F，Zhao J Z，Weng H M，Fang Z，Dai X.Phys. Rev.Lett.，2013，110(9)：096401

[11]张广铭，于渌.物理，2007，36(6)：434-442

[12]Meissner W，Voight G.Ann.Phys.，1930，7：892-936

[13]Sarachik M P，Corenzwit E，Longinotti L D.Phys. Rev.，1964，135(4A)：A1041-A1045

[14]Kondo J.J.Phys.Soc.Jpn.，2005，74(1)：1-3

[15]Kondo J.Prog.Theor.Phys.，1964，32(1)：37-49

[16]Hewson A C.The Kondo Problem to Heavy Fermions，Cambridge Univ.Press，1993

[17]Kouwenhoven L，Glazman L.Phys.World，2001，Jan.：33-38

[18]Andres K，Graebner J E，Ott H R.Phys.Rev.Lett.，1975，35(26)：1779-1782

[19]Steglich F，Aarts J，Bredl C D，Lieke W，Meschede D，Franz W，Schfer H.Phys.Rev.Lett.，1979，43(25)：1892-1986

[20]Ott H R，Rudigier H，Fisk Z，Smith J L.Phys.Rev. Lett.，1983，50(20)：1595-1598

[21]Stewart G R，Fisk Z，Willis J O，Smith J L.Phys. Rev.Lett.，1984，52(8)：679-682

[22]Doniach S.Physica B，1977，91B：231-234

[23]Ruberman M A，Kittle C.Phys.Rev.，1954，96(1)：99-102

[24]Kasuya T.Prog.Theor.Phys.，1956，16(1)：58-63

[25]Yosida K.Phys.Rev.，1969，106(5)：893-898

[27]Read N，Newns D M.J.Phys.C，1983，16：3273-3295

[28]Coleman P.Phys.Rev.B，1984，29(6)：3035-3044

[29]Read N，Newns D M，Doniach S.Phys.Rev.B，1984，30(7)：3841-3844

[30]Millis A J，Lee P A.Phys.Rev.B，1987，35(7)：3394-3414

[31]Auerbach A，Levin K.Phys.Rev.Lett.，1986，57(7)：877-880

[32]Zhang G M，Yu L.Phys.Rev.B，2001，62(1)：76-79

[33]Li G B，Zhang G M.Phys.Rev.B，2010，81(9)：094420

[34]Si Q，Rabello S，Ingersent K，Smith J L.Nature(London)，2001，413：804-808

[35]Shim J H，Haule K，Kotliar G.Science，2007，318(12)：1615-1617

[36]Haule K，Yee C H，Kim K.Phys.Rev.B，2010，81(19)：195107

[37]Capponi S，Assaad F F.Phys.Rev.B，2001，63(15)：155114

[38]Senthil T，Vojta M，Sachdev S.Phys.Rev.B，2004，69(3)：035111

[42]Abrahams E，Schmalian J，Wlfle P.Phys.Rev.B，2014，90(4)：045105

[43]Gorter C J，Casimir H B G.Physica，1934，1(1-6)：306-320

[44]Landau L D，Lifshitz E M.Statistical Physics I，Oxford：Pergomon Press，1980

[45]Nakatsuji S，Pines D，Fisk Z.Phys.Rev.Lett.，2004，92(1)：016401

[46]Curro N J，Young B L，Schmalian J，Pines D.Phys. Rev.B，2004，70(23)：235117

[47]Yang Y F，Pines D.Phys.Rev.Lett.，2008，100(9)：096404

[48]Yang Y F，Fisk Z，Lee H O，Thompson J D，Pines D. Nature(London)，2008，454：611-613

[49]Yang Y F，Pines D.Proc.Nal.Acad.Sci.USA，2012，109(45)：E3060-E3066

[50]John D C.Phys.Rev.Lett.，1989，62(8)：957-960

[51]Nakano T，Oda M，Manable C，Momono N，Miura Y，Ido M.Phys.Rev.B，1994，49(22)：16000-16008

[52]Barzykin V，Pines D.Phys.Rev.Lett.，2006，96(24)：247002

[53]Barzykin V，Pines D.Adv.Phys.，2009，58(1)：1-65

[54]Pines D.J.Phys.Chem.B，2013，117：13145-13153

[55]Ma L，Ji G F，Dai J，He J B，Wang D M，Chen G F，Normand B，Yu W Q.Phys.Rev.B，2011，84(22)：220505(R)

[56]Ji G F，Zhang J S，Ma L，Fan P，Wang P S，Dai J，Tan G T，Song Y，Zhang C L，Dai P C，Normand B，Yu W Q.Phys.Rev.Lett.，2013，111(10)：107004

[57]Dai P C，Hu J P，Dagotto E.Nat.Phys.，2012，8(10)：709-718

[58]Wang M，Zhang C L，Lu X Y，Tan G T，Luo H Q，Song Y，Wang M Y，Zhang X T，Goremychkin E A，Maier T A，Yin Z P，Haule K，Kotliar G，Dai P C. Nat.Commun.，2013，4：2874

[59]You Y Z，Weng Z Y.New J.Phys.，2014，16(2)：023001

[60]Mito T，Kawasaki S，Kawasaki Y，Zheng G Q，Kitaoka Y，Aoki D，Haga Y，Onuki Y.Phys.Rev.Lett.，2003，90(7)：077004

[61]Curro N J.Rep.Pro.Phys.，2009，72：026502

[62]杨义峰.物理，2014，43(2)：80-87

[63]Moriya T.Prog.Theor.Phys.，1956，16(1)：23–44

[64]Yang Y F，Urbano R，Curro N J，Pines D，Bauer E D.Phys.Rev.Lett.，2009，103(19)：197004

[65]Yang Y F，Pines D，Curro N J.arXiv：1410.0452

[66]Fert A，Levy P M.Phys.Rev.B，1987，36(4)：1907-1916

[67]Hundley M F，Malinowski A，Pagliuso P G，Sarrao J L，Thompson J D.Phys.Rev.B，2004，70(3)：035113

[68]Yang Y F.Phys.Rev.B，2013，87(4)：045102

[69]Park W K，Greene L H.J.Phys.Condens.Matter，2009，21(10)：103203

[70]Schmidt A R，Hamidian M H，Wahl P，Meier F，Balatsky A V，Garrett J D，Williams T J，Luke G M，Davis J C.Nature(London)，2010，465(7298)：570-576

[71]Ernst S，Kirchner S，Krellner C，Geibel C，Zwicknagl G，Steglich F，Wirth S.Nature(London)，2011，474(7351)：362-366

[72]Aynajian P，da Silva Neto E H，Gyenis A，Baumbach R E，Thompson J D，Fisk Z，Bauer E D，Yazdani A.Nature(London)，2012，486(7402)：201-206

[73]Moser M，Wachter P，Franse J J，Meisner G P，Walker E.J.Magn.Magn.Mater.，1986，54：373-374

[74]Hasselbach K，Kirtley J R，Lejay P.Phys.Rev.B，1992，46(9)：5826-5829

[75]Park W K，Sarrao J L，Thompson J D，Greene L H. Phys.Rev.Lett.，2008，100(17)：177001

[76]Yang Y F.Phys.Rev.B，2009，79(24)：241107(R)

[77]Fano U.Phys.Rev.，1961，124(6)：1866-1878

[78]Maltseva M，Dzero M，Coleman P.Phys.Rev.Lett.，2009，103(20)：206402

[80]Lee W C，Park W K，Arham H Z，Greene L H，Phillips P.Proc.Nal.Acad.Sci.USA，2015，112(3)：651–656

[81]Park W K，Tobash P H，Ronning F，Bauer E D，Sarrao J L，Thompson J D，Greene L H.Phys.Rev.Lett.，2012，108(24)：246403

[83]Aynajian P，da Silva Neto E H，Parker C V，Huangb Y，Pasupathyc A，Mydoshd J，Yazdania A.Proc.Nal. Acad.Sci.USA，2010，107(6)：10383-10388

[84]Zhang X H，Butch N P，Syers P，Ziemak S，Greene R L，Paglione J.Phys.Rev.X，2013，3(1)：011011

[85]Rossler S，Jang T H，Kim D J，Tjeng L H，Fisk Z，Steglich F，Wirth S.Proc.Nat.Acad.Sci.USA，2014，111(4)：4798-4802

[86]Yang Y F，Pines D.Proc.Nal.Acad.Sci.USA，2014，111(12)：18178-18182

[87]Shirer K R，Shickley A C，Dioguardi A P，Crocker J，Lin C H，apRoberts-Warren N，Nisson D M，Klavins P，Cooley J C，Yang Y F，Curro N J.Proc.Nal.Acad. Sci.USA，2012，109(45)：E3067-E3073

[88]apRoberts-Warren N，Dioguardi A P，Shockley A C，Lin C H，Crocker J，Klavins P，Pines D，Yang Y F，Curro N J.Phys.Rev.B，2011，83(6)：060408(R)

[89]Shishido H，Settai R，Harima H，Onuki Y.Physica B，2006，92：378–380

[92]Aso N，Ishii K，Yoshizawa H，Fujiwara T，Uwatoko Y，Chen G F，Sato N K，Miyake K.J.Phys.Soc.Jpn.，2009，78(7)：073703

[93]Llobet A，Gardner J S，Moshopoulou E G，Mignot J M，Nicklas M，Bao W，Moreno N O，Pagliuso P G，Goncharenko N，Sarrao J L，Thompson J D.Phys. Rev.B，2004，69(2)：024403

[94]Hegger H，Petrovic C，Moshopoulou E G，Hundley M F，Sarrao J L，Fisk Z，Thompson J D.Phys.Rev.Lett.，2000，84(21)：4986-4989

[95]Park T，Ronning F，Yuan H Q，Salamon M B，Movshovich R，Sarrao J L，Thompson J D.Nature (Londo)2005，440(2)：65-68

[96]Ishida K，Okamoto K，Kawasaki Y，Kitaoka Y，Trovarelli O，Geibel C，Steglich F.Phys.Rev.Lett.，2002，89(10)：107202

[97]Ronning F，Capan C，Bauer E D，Thompson J D，Sarrao J L，Movshovich R.Phys.Rev.B，2006，73(6)：064519

[98]Yang Y F，Pines D.Proc.Nal.Acad.Sci.USA，2014，111(6)：8398-8403

[99]Urbano R R，Young B L，Curro N J，Thompson J D，Pham L D，Fisk Z.Phys.Rev.Lett.，2007，99(14)：146402

[100]Sidorov V A，Nicklas M，Pagliuso P G，Sarrao J L，Bang Y，Balatsky A V，Thompson J D.Phys.Rev. Lett.，2002，89(15)：157004

[101]Stockert O，Steglich F.Annu.Rev.Condens.Matter Phys.，2011，2：79-99

[102]Scalapino D J.Rev.Mod.phys.，2012，84(4)：1383-1417

[103]Kohori Y，Taira H，Fukazawa H，Kohara T，Iwamoto Y，Matsumoto T，Maple M B.J.Alloys Compd.，2006，408–412：51-53

[104]Dyke J S V，Massee F，Allan M P，Davis J C S，Petrovic C，Morr D K.Proc.Nal.Acad.Sci.USA，2014，111(32)：11663-11667

[105]Curro N J，Caldwell T，Bauer E D，Morales L A，Graf M J，Bang Y，Balatsky A V，Thompson J D，Sarrao J L.Nature(London)，2005，434：622-625

[106]Mo S K，Lee W S，Schmitt F，Chen Y L，Lu D H，Capan C，Kim D J，Fisk Z，Zhang C Q，Hussain Z，Shen Z X.Phys.Rev.B，2012，85(24)：241103(R)

[107]Ohishi K，Heffner R H，Ito T U，Higemoto W，Morris G D，Hur N，Bauer E D，Sarrao J L，Thompson J D，MacLaughlin D E，Shu L.Phys.Rev.B，2009，80(12)：125104

[108]Kambe S，Tokunaga，Sakai H，Chudo H，Haga Y，Matsuda T D，Walstedt R E.Phys.Rev.B，2010，81(14)：140405(R)

[109]Shockley A C，apRoberts-Warren N，Nission D M，Kuhns P L，Reyes A P，Yaun S，Curro N J.Phys. Rev.B，2013，88(7)：075109

[110]Tran L M，Nowak B，Tran V H.Phys.Rev.B，2011，84(22)：224406

[111]Li M R，Retuerto R，Deng Z，Sarkar T，S´anchez-Ben´ıtez J，Croft M C，Dasgupta T S，Das T，Tyson T A，Walker D，Greenblatt M.Chem.Mat.，2015，27：211

[112]Barzykin V.Phys.Rev.B，2006，73(9)：094455

[113]Choi H C，Min B I，Shim J H，Haule K，Kotliar G. Phys.Rev.Lett.，2012，108(1)：016402

[114]Zhu L J，Zhu J X.Phys.Rev.B，2011，83(19)：195103

[115]Jiang M，Curro N J，Scalettar R T.Phys.Rev.B，2014，90(24)：241109(R)

[116]Xie N，Yang Y F.Phys.Rev.B，2015，91(19)：195116

The dual(simultaneously localized and itinerant)nature of strongly correlated electrons can be traced back to the particle-wave duality in quantum mechanics and is the origin of numerous exotic quantum phenomena in correlated materials.Here we discuss the various experimental aspects of this dual behavior of f-electron and focus on the phenomenological two-fluid theory recently developed for heavy fermion materials.The two-fluid theory has been quite successful in explaining many puzzling experiments and revealing the common nature of the complex behaviors of many heavy fermion compounds.It provides a new avenue for understanding the exotic properties of strongly correlated systems including cuprates and iron-based superconductors and demands further theoretical and experimental investigations.

Two-fluid theory for heavy fermion materials

Yang Yi-Feng1，2∗，Xie Neng1，Li Yu1
1.Beijing National Laboratory for Condensed Matter Physics and Institute of Physics，Chinese Academy of Sciences，Beijing 100190，China 2.Collaborative Innovation Center of Quantum Matter，Beijing 100190，China

strongly correlated electrons；heavy fermions；two-fluid theory

date：2015-08-26

O469

10.13725/j.cnki.pip.2015.05.002

*yifeng@iphy.ac.cn

1000-0542（2015）05-0191-21191