微型激波管内部激波特性的数值模拟

张 光，崔宝玲，金英子，金羲東

（1.浙江理工大学浙江省流体传输技术研究重点实验室，杭州310018；2.安东国立大学机械工程学院，韩国安东760749）

微型激波管内部激波特性的数值模拟

张 光1，崔宝玲1，金英子1，金羲東2

（1.浙江理工大学浙江省流体传输技术研究重点实验室，杭州310018；2.安东国立大学机械工程学院，韩国安东760749）

为了研究微型激波管内部的不稳定流动和激波运动特性，采用数值模拟的方法对微型激波管内部流动进行分析。对比分析不同隔膜压力比（高压腔与低压腔的初始压力之比）和激波管直径对微型激波管内激波、交接面以及流体运动特性的影响，并与实验数据进行比较。结果表明：随着隔膜压力比的增大，激波和交接面的运动速度逐渐增大；激波在微型激波管内运动时，其强度逐渐减弱；在低压被驱动腔内压强较低时，观察到厚度较大的边界层，这说明低压影响对微型激波管内的激波和流体运动会产生一定的能量损失；激波前后的压力梯度随着激波运动逐渐减小；交接面在微型激波管内运动时，运动速度逐渐增大；参数S值可以反映微型激波管内的低压和小尺寸影响。

微型激波管；激波；交接面；非定常流动；数值模拟

0　引 言

近年来，微型激波管已广泛用于机械和生物工程设备中，如微型发动机、微型燃烧机、无针注射等。与传统的激波管类似，微型激波管由隔膜隔开的高压腔和低压腔组成，高压腔也称为驱动腔，低压腔称为被驱动腔。由于高压腔与低压腔之间的压力差，隔膜的瞬间破裂会使激波管内产生不稳定的激波流动。如果压力足够大，隔膜将会自行破裂，否则需要用手动的方式使隔膜破裂。隔膜破裂产生的激波和交接面会向低压腔运动，而产生的膨胀波向高压腔运动。在微型激波管内，含有运动激波的可压缩流动需要更多地考虑耗散带来的影响，而在大型激波管内可以忽略这种影响。

在过去的一个世纪里，尽管许多学者不断努力研究微型激波管内部流动，但仍然存在一些没有探究和无法解释的现象。在微型激波管内，由低压和小尺寸产生的稀疏影响表现得尤为明显，该影响使激波强度逐渐衰弱，而在大型激波管内可以忽略这种影响；流体的粘性影响和激波与壁面之间的摩擦也使激波产生更多的能量损失。因此，关于产生激波强度损失的原因一直是国内外学者研究的重点［1-6］。文献［1-3］采用试验的方法探究了微型激波管内激波强度衰减的原因，结果表明：激波管内粘性影响、边界层的发展以及壁面摩擦是导致试验过程中激波强度损失的主要原因。微型激波管内边界层的发展使激波和交接面的运动与理论预测产生一定的偏差。交接面是假想隔开高压腔气体与被激波加热气体的一个面。在交接面两边，气体压强和速度大小相等，而温度和密度不同。在边界层的作用下，激波运动速度逐渐减小，而交接面速度逐渐增大。Sturtevant等［7］、Tanaki等［8］运用数值模拟的方法探究了不同边界条件下边界层对激波运动的影响；Mirels［9］和Roshko［10］采用理论分析的方法研究了微型激波管内的边界层效应，并提出了能够预测边界层效应的理论模型。

与传统的大型激波管相比，尺寸对微型激波管内激波和流体的运动特性影响极大。Brouillette［11］采用试验方法探究了微小尺寸激波管内可压缩的湍流，引入控制体法，并提出表明小尺寸影响的一个参数S。在S较小的条件下，分析了微型激波管内摩擦和热传递产生的扩散影响，结果表明：控制体模型能够有效预测小尺寸对激波强度的影响。但作者没有给出S值随时间的变化情况。Park等［12］和Sun等［13］运用试验的方法研究了不同直径的微型激波管内激波运动，所得到的实验结果与理论预测基本一致。Zeitoun等［14-15］采用数值模拟的方法探究了包含与速度滑移和温度跳跃的边界条件相耦合的湍流纳维-斯托克斯方程在微型激波管内部流动方面的应用。Arun等［16-17］对不同边界条件下的微型激波管进行数值模拟，并与理论预测进行比较，数值模拟结果与理论结果相吻合。

本文采用数值模拟的方法对微型激波管内激波和交接面的运动特性进行分析，并揭示不同边界条件下激波强度损失的原因。采用CFD软件Fluent进行数值模拟。保持高压腔的压力为大气压强不变，改变低压腔的压力，从而探究不同隔膜压力比对激波运动的影响；采用不同直径的激波管来研究尺寸对激波管内部流动特性的影响；将数值模拟结果与实验结果进行对比，从而验证数值模拟方法的正确性；通过计算得到激波与交接面之间的距离，进而得到反应尺寸影响的参数S的变化情况。

1　计算模型及数值方法

1.1计算模型

本文中数值模拟采用的计算模型如图1所示。采用2维轴对称模型，高压腔和低压腔都采用理想气体作为工作流体，高压腔气体压强为P4，低压腔气体压强为P1。定义隔膜压力比（diaphragm pressure ratio，DPR）为P4/P1。管内截面为圆形，直径用D来表示，高压腔长度L4为100 mm，低压腔长度L1为200 mm。X表示轴线方向的位移，向右为正方向。

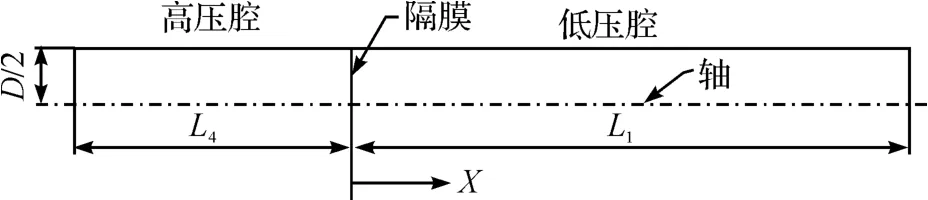
图1　数值模拟的计算模型

2.2数值方法

为了研究微型激波管内部详细的非定常流动，本文采用结构化四边形网格，并在壁面附近创建边界层网格。合适的边界层网格有助于在数值模拟过程中观察边界层形成对激波运动的影响。假设高压腔和低压腔的工作流体为理想气体；采用非定常的雷诺平均纳维-斯托克斯方程来分析计算流体运动特性，湍流模型选用SST k-ω模型，粘度模型采用包含流体粘度随温度变化的萨瑟兰粘度模型；采用AUSM格式作为通量格式，时间离散选用二阶隐性格式，空间离散采用二阶迎风格式。

2.3边界条件

在不同的隔膜压力比和激波管直径下，采用数值模拟的方法分析了微型激波管内部流动。边界条件如表1所示，高压腔和低压腔的温度都初始化为300 K。模型网格数量为163000，非定常迭代计算的时间步长由最小的计算网格尺寸决定，设定为10-8s。隔膜的初始边界条件为壁面，在改变其边界条件为交互面的过程中，这一过程可视为隔膜瞬间破裂的过程。管壁采用绝热无滑移壁面，并且管壁温度保持300K不变。因此，在数值模拟过程中，工作流体与激波管管壁之间不会产生热传递。数值模拟编号表示在不同边界条件下进行的数值模拟，本文采用四种不同的边界条件来模拟微型激波管内部流体的运动特性。

表1　不同数值模拟条件下的参数值

2.4方法验证

为了验证数值模拟方法的正确性，将数值模拟的结果与实验数据进行对比。文献［12］采用直径为6mm的激波管，在隔膜压力比为6、低压腔初始压强为大气压强的条件下进行试验。本文数值模拟中采用相同的边界条件，结果对比曲线如图2所示。EH代表膨胀波头部，SW代表激波。横坐标代表激波和膨胀波头部运动的位移，X/D表示激波和膨胀波头部沿轴向运动的无因次位移，纵坐标表示运动时间。数值模拟结果与试验结果存在一定的偏差，这种偏差是由在试验过程中实际流体的粘性以及管内高温气体与激波管壁面之间的热传递导致的。在试验过程中，激波会加热其运动过后区域内的气体，高温气体会与激波管管壁之间产生热传递，但在数值模拟中，这种热传递不会发生，故激波和膨胀波在试验过程中产生更多的强度损失。在运动的激波后面会产生湍流边界层，这也是其强度产生衰减的一个主要原因。以上原因说明数值模拟结果与实验结果之间的偏差是合理的，本文采用的数值方法是可靠的。因此，目前的数值模拟方法能用来预测微型激波管内激波运动特性。

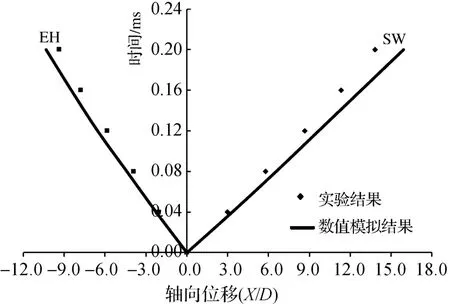
图2　数值模拟与试验结果随时间变化的对比曲线

2　理论分析

2.1激波管理论

当微型激波管内的薄膜破裂，会产生激波、交接面以及膨胀波。由无粘激波管理论可知，微型激波管内流体粘度可以忽略不计；工作流体为理想气体；气体绝热指数为常数（γ=1.4）。根据高压腔与低压腔的初始压力之比，激波和交接面向低压腔运动的马赫数可用式（1）和式（2）计算得到［11］。

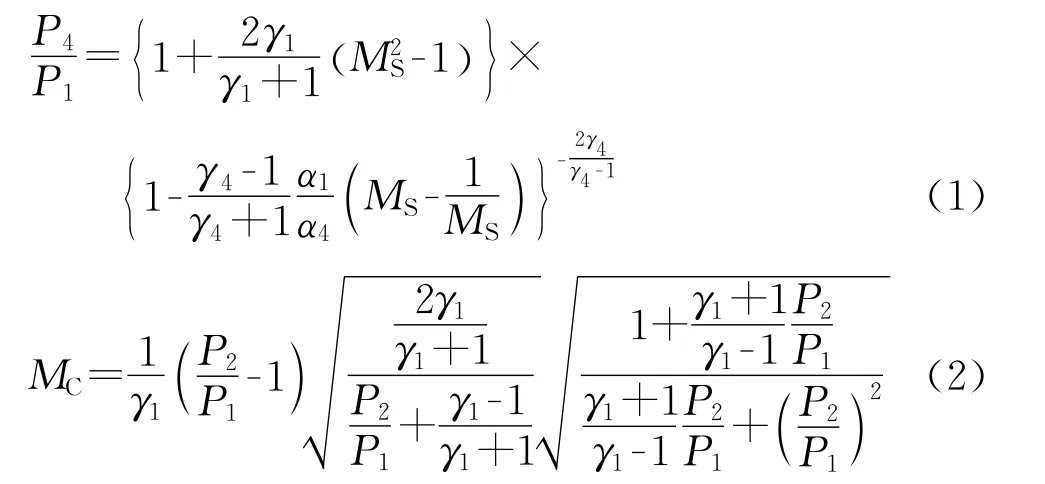
其中：MS为激波运动马赫数，MC为交接面运动马赫数；γ1和γ4分别表示低压腔和高压腔内气体的绝热指数；a1和a4分别代表低压腔和高压腔气体声速大小；P2是激波与交接面之间区域的压强值。

式（1）和（2）表明：随着隔膜压力比的增大，激波和交接面运动的马赫数也逐渐增大。但由于流体的粘性影响和激波管内存在的稀疏影响，数值模拟得到的结果与理论预测的结果往往存在一定的偏差。

2.2尺寸影响参数S

Brouillette［11］发现，包含热传导和剪切力等扩散传递现象是导致数值模拟流体特性与理论预测有明显偏差的主要原因。他提出了控制体分析法，控制体是一个取自激波与交接面之间区域的单元体，通过对控制体内流体特性进行分析，以说明激波管内部的尺寸影响和扩散传递现象。控制体的选取如图3所示，EW表示膨胀波，CS表示交接面，SW表示激波。根据控制体分析法，表示尺寸影响的参数S取自于式（3），参数S的具体表达如式（4）所示。由式（3）可知，较小的S值会对计算激波前后的密度比会产生更大的影响。激波与交接面之间区域雷诺数Re和两者之间的距离L是计算S必需的两个参数，随着Re的减小和L的增大，S值会减小；如果S变得无限大，那么可以忽略尺寸影响。

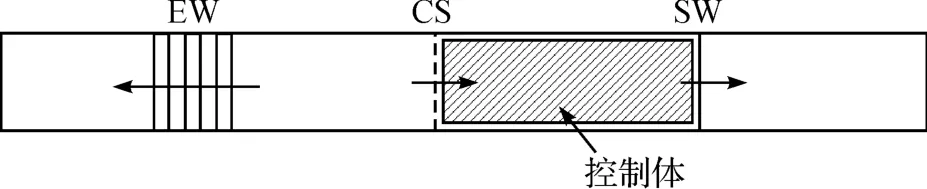
图3　用于分析激波管内扩散影响的控制体模型

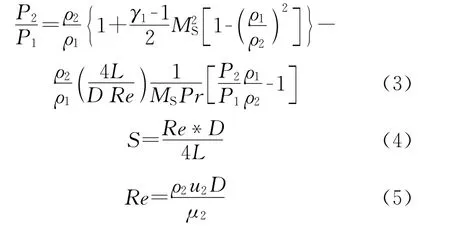
其中：ρ1与ρ2分别表示激波前后的流体密度；Re和Pr分别代表雷诺数和普朗特数；D代表激波管直径；L表示激波与交接面之间的距离；u2和μ2分别表示激波与交接面之间区域流体的速度和动力粘度。Re由式（5）计算得到。理论上，激波与交接面之间流体速度是相同的，但由于边界层的存在，靠近壁面的流体速度相对较小，在本文Re的计算中，取交接面的运动速度为u2。

2.3激波前后的压力梯度

随着激波在激波管内运动，其前后的压力梯度也发生变化。当隔膜破裂0.12ms后，激波前后的局部压力分布如图4所示。激波前后的压力梯度与其前后的压强差以及压强变化的距离有关，如式（6）所示。式（7）中C表示激波前后压力梯度的无量纲值，称其为标准化压力梯度（normalized pressure gradient，NPG）。由于激波强度随时间变化逐渐衰弱，激波前后压强差会逐渐减小，故其前后压力梯度也不断减小。

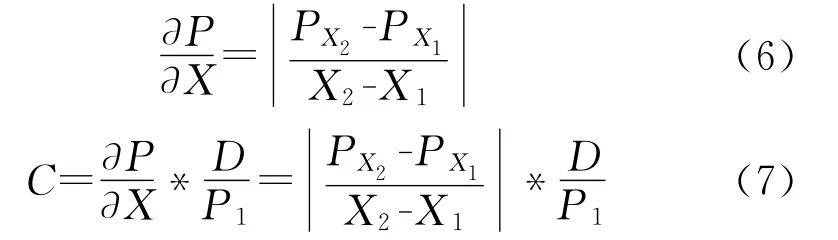
图4　微型激波管内沿轴线方向的局部压强变化

3　结果与分析

如表1所示，在隔膜压力比分别为10、20和100的条件下，探究直径为3 mm的激波管内激波运动的特征。当膨胀波头部没有运动到驱动腔的进口壁面时，激波管内流体沿轴线方向的压力变化曲线如图5所示。图5（a）-（c）分别表示在DPR为10、20和100时，微型激波管流体沿轴线方向的压力变化。纵坐标表示静压比，静压比是流体静压与低压腔内流体的初始静压之比；横坐标表示轴向位移。随着激波向前运动，受激波管内流体粘度以及激波前端与壁面之间的摩擦的影响，其强度逐渐减弱。当DPR为100时，激波在同一时刻运动的位移比DPR为10和20时要大，这说明，随着隔膜压力比的增大，激波运动的速度也会增大，这与式（1）的预测相吻合。

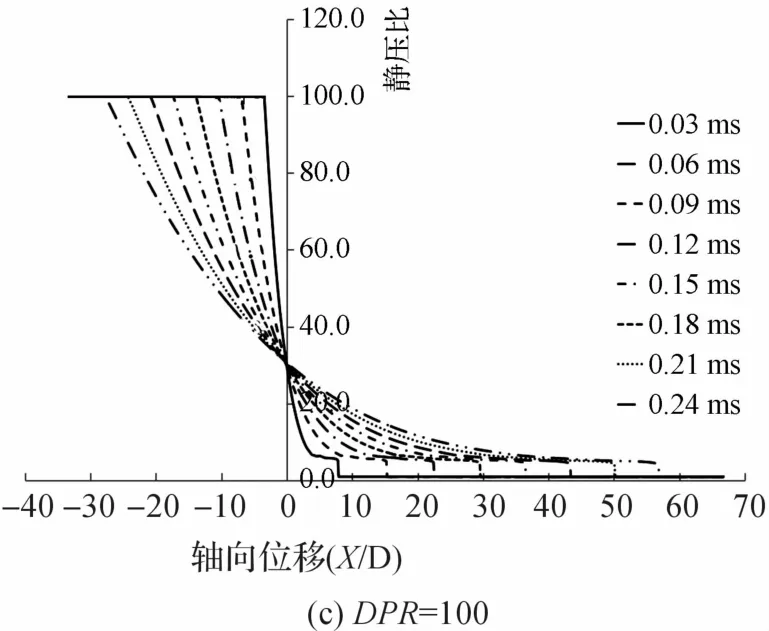
图5　不同隔膜压力比下激波管内沿轴线方向的压力变化曲线

激波前后的无量纲压力梯度由式（7）计算得到，标准化压力梯度的变化曲线如图6所示。随着激波向低压腔运动，NPG逐渐减小，这主要是由于激波在运动过程中，其强度不断减弱，导致其前后的压强差逐渐减小。激波运动的初始阶段，NPG衰减得更快，这是由于在初始阶段激波前后压强变化的距离|X2-X1|显著增大。当激波运动一段位移后（X/D＞30），其前后压力梯度变化逐渐减小，而这种变化可以视作线性变化。

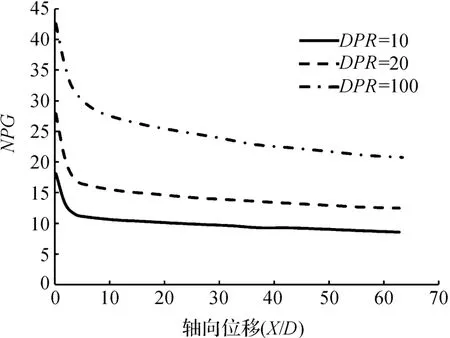
图6　不同隔膜压力比下激波前后压力梯度的变化曲线

在不同DPR的条件下，由式（5）计算得到的激波与交接面之间区域的雷诺数变化如图7所示。在这个区域内，随着激波和交接面向前运动，流体密度、速度与动力粘度发生改变。在三种不同DPR的条件下，Re都逐渐增大，这是由于激波与交接面之间区域流体速度逐渐增大，流体密度也逐渐增大。由于该区域流体温度会升高，动力粘度也会变大，但流体粘度变大的趋势没有速度和密度变大的趋势明显，故Re总体变化还是逐渐增大的。当DPR为100时，Re比DPR为10和20时要小。这是由于在大DPR下，P4保持大气压强不变，较小的P1导致较小的流体密度，而较小的密度导致较小的雷诺数。

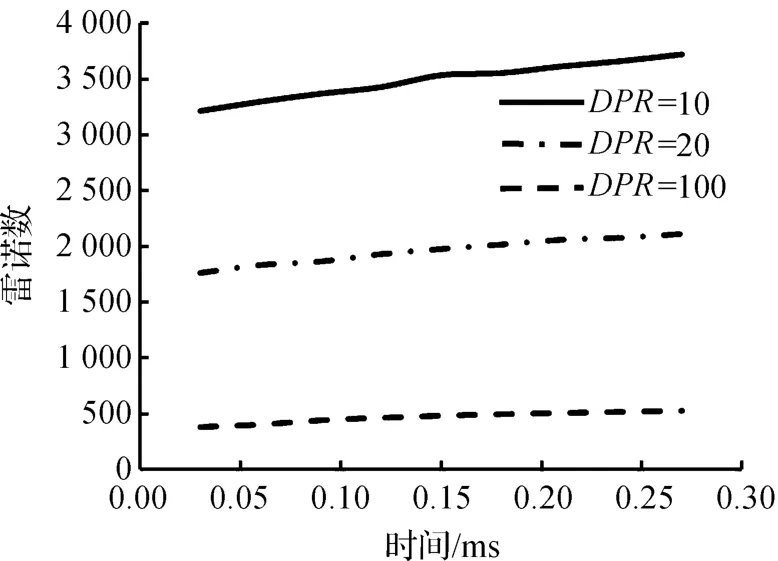
图7　不同隔膜压力比下激波与交接面之间区域雷诺数的变化曲线

在不同DPR的条件下，由式（4）计算得到的S值变化曲线如图8所示。在三种情况下，S值都逐渐减小，这是由于激波和交接面之间存在速度差，导致两者之间的距离L逐渐增大。当DPR为10时，S值比DPR为20和100时要大。当DPR较小时，雷诺数较大，激波和交接面之间的速度差较小，这导致L也较小。较小的S值能够表明微型激波管内的尺寸影响，而这种尺寸影响会使激波强度衰减更快。在被驱动腔压强较小的情况下，计算得到较小的S值，这说明S值同样也可以用来衡量激波管内低压对激波运动的影响。

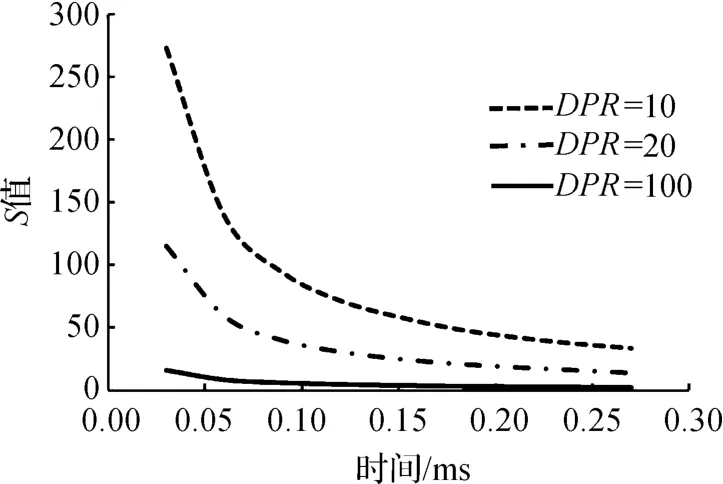
图8　不同的隔膜压力比下S值的变化曲线

在不同的DPR下，当隔膜破裂0.03ms后，交接面前后流体的温度分布以及交接面的位移如图9所示。等温线图能够准确地反映流体内部的边界层厚度。如图9所示，BL表示边界层。边界层是由于流体粘度而产生的；是流体在靠近壁面形成的薄流层。在边界层内，靠近壁面的流体速度为0，沿远离壁面的垂直方向，流体速度逐渐增大，并达到一恒定值。如图9所示，在温度云图中，边界层的厚度定义为从壁面到流体温度达到恒定值的距离。当DPR较大时，交接面运动的位移也相对较大，即交接面运动的速度较大，这与式（2）的预测是相吻合的。与DPR为10和20相比，当DPR为100时，激波管内边界层的厚度更大，这是因为在DPR较大时，P1较小，由低压导致的稀疏影响使微型激波管内边界层变厚。厚度较大的边界层使激波强度衰减更快，同时使激波后面的流体产生更多的能量耗散和粘性损失。

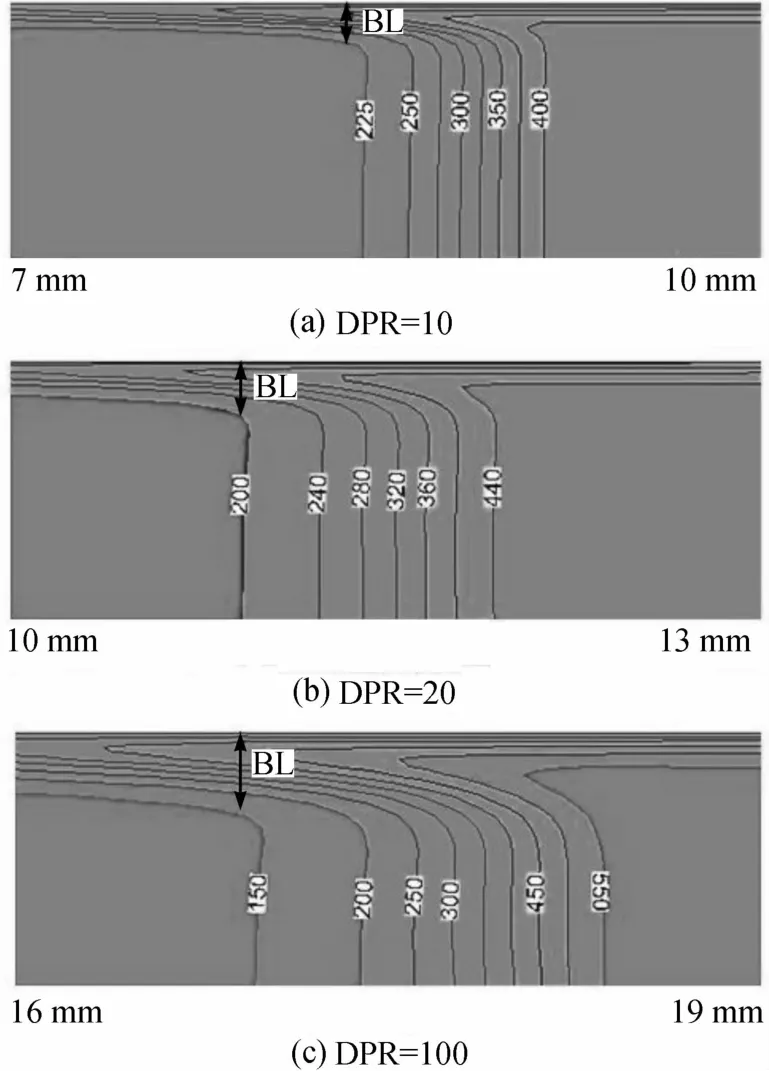
图9　不同隔膜压力比下交接面前后的温度分布

在不同直径的激波管内，激波与交接面的速度变化曲线如图10所示。激波的运动速度在两种激波管内都逐渐减小，这是由激波前端与激波管壁面之间的摩擦、流体内部粘性以及激波后面边界层的形成导致的。在小直径的激波管内，激波速度衰减得更快，这是由微型激波管内的小尺寸影响导致的。交接面的运动速度在两种激波管内都逐渐增大。在微型激波管内，边界层随着激波的运动在其后面逐渐形成，当交接面以马赫数大于1的速度在激波管内部运动时，边界层使交接面在一个超声速喷管内运动，故速度会增加。在小直径的激波管内，交接面的运动速度增加得更快，这是由于小直径激波管内形成厚度更大的边界层。

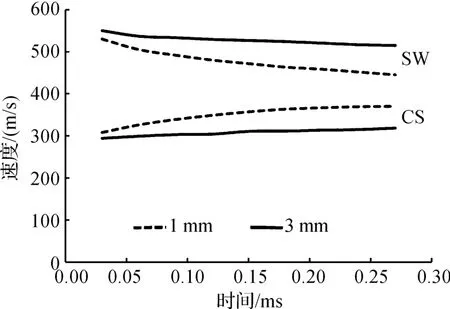
图10　不同激波管直径下激波与交接面速度的变化曲线

在不同直径的激波管内，S值的变化曲线如图11所示。在两种激波管内，S值都随着时间变化而减小，这是由于随着激波与交接面向前运动，L会逐渐增大。由式（3）可知，较小的S值对计算激波前后的密度之比是有更明显影响的。在直径较小的激波管内，S值明显较小，激波强度损失也更大，这与预测结果是一致的。这说明用S值来衡量微型激波管内的尺寸影响是可行的。

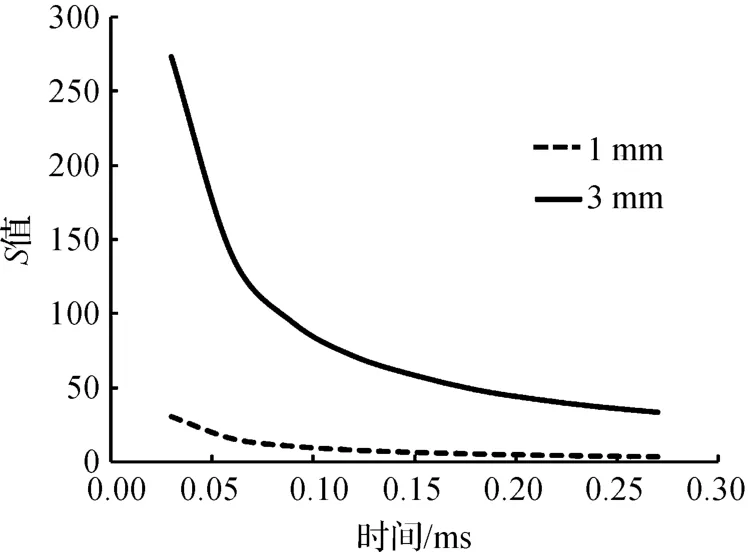
图11　不同激波管直径下S值的变化曲线

4　结 论

在不同隔膜压力比和激波管直径的条件下，采用数值模拟的方法来研究微型激波管内的激波、交接面以及流体运动特性，结果表明：随着隔膜压力比增大，激波强度逐渐增大，激波在激波管内的运动速度也逐渐增大，交接面的运动速度也逐渐增大；激波在激波管内运动时，其强度逐渐减弱；在被驱动腔压强较低的情况下，观察到厚度较大的边界层，这说明低压影响对微型激波管内的流体以及激波运动会产生更多能量损失；随着激波在激波管内运动，其强度逐渐衰弱以及其两边压强变化的距离逐渐变大，这使激波前后的压力梯度随着时间变化逐渐减小；交接面在微型激波管内运动时，其运动速度逐渐增大，这是由运动激波后面边界层的形成导致的；激波在低压和小直径的激波管内运动时，激波强度衰减得更快，并且计算得到较小的S值，这表明S值可以反映微型激波管内的低压和小尺寸影响。

［1］Duff R E.Shock tube performance at initial low pressure［J］.Phys Fluids，1959，2（1）：207-216.

［2］Ngomo D，Chaudhuri A，Chinnayya A，et al.Numerical study of shock propagation and attenuation in narrow tubes including friction and heat losses［J］.Computers &Fluids，2010，39（9）：1711-1721.

［3］Xiao H，Toshiyuki A，Naoya T.The feature of weak shock wave propagated in an overlong tunnel［J］.Open Journal of Fluid Dynamics，2012，2（4）：285-289.

［4］Mirshekari G，Brouillette M.One-dimensional model for microscale shock tube flow［J］.Shock Waves，2009，19（1）：25-38.

［5］Watvisave D S，Bhandarkar U V，Puranik B P.Effects of wall conduction and rarefaction on shock propagation in a micro-channel［J］.Shock Waves，2014，24（3）：295-306.

［6］Huynh D.The shock tube problem from a combined experimental and computational perspective［C］∥21th AIAA Computational Fluid Dynamics Conference.San Diego，California，USA，2013，3：2442-2458.

［7］Sturtevant B，Okamura T T.Dependence of shock tube boundary layers on shock strength［J］.Phys Fluids，1969，12（8）：1723-1725.

［8］Tanaki K，Inaba K，Yamamoto M.Numerical investigation on transition of shock induced boundary layer［C］∥47th AIAA Aerospace Science Meeting Including the New Horizons Forum and Aerospace Exposition.Orlando，Florida，2009：5-8.

［9］Mirels H.Test time in low pressure shock tubes［J］. Phys Fluids，1963，6（9）：1201-1214.

［10］Roshko A.On flow duration in low pressure shock tubes［J］.Phys Fluids，1960，3（6）：835-842.

［11］Brouillete M.Shock waves at microscales［J］.Shock Waves，2003，13（1）：3-12.

［12］Park JO，Kim G W，Kim H D.Experimental study of the shock wave dynamics in micro shock tube［J］. Journal of the Korean Society of Propulsion Engineers，2014，17（5）：54-59.

［13］Sun M，Ogawa T，Takayama K.Shock propagation in narrow channels［C］∥Processing of 24th International Symposium on Shock Waves.Tohoku University，Katahira，Japan，2001：1321-1327.

［14］Zeitoun D E.Microsize and initial pressure effects on shock wave propagation in a tube［J］.Shock Waves，2014，24（5）：515-520.

［15］Zeitoun D E，Burtschell Y.Navier-Stokes computations in micro shock tubes［J］.Shock Waves，2006，15（3）：241-246.

［16］Arun K R，Kim H D.Computational study of the unsteady flow characteristics of a micro shock tube［J］.Journal of Mechanical Science and Technology，2013，27（2）：451-459.

［17］Arun K R，Kim H D.Numerical visualization of the unsteady shock wave flow field in micro shock tube［J］.Journal of the Korean Society of Visualization，2012，10（1）：40-46.

Numerical Simulation of Shock Wave Characteristics in Micro Shock Tubes

ZHANGGuang1，CUI Bao-ling1，JIN Ying-zi1，KIM Heuy-dong2
（1.The Zhejiang Provincial Key Laboratory of Fluid Transmission Technology Research，Zhejiang Sci-Tech University，Hangzhou 310018，China；2.Department of Mechanical Engineering，Andong National University，Andong 760749，Republic of Korea）

Numerical simulation was applied to study internal flow of micro shock tube in order to study unsteady flow and shock wave motion characteristics in micro shock tube.Contrastive analysis was conducted for effects of different diaphragm pressure ratio（initial pressure ratio of high-pressure cavity and low-pressure cavity），and shock tube diameter on shock wave in micro shock tube，contact surface and fluid motion characteristics.Besides，experimental data were compared.The results show motion speed of shock wave and contact surface increases gradually with the increase in the diaphragm pressure ratio；when shock wave moves in micro shock tube，shock wave strength gradually weakens；a thick boundary layer is observed when pressure intensity in low-pressure driven cavity，which indicates that low pressure effect makes shock wave and flow more energy lose；pressure gradient in the front of and after shock wave gradually decreases as shock wave motion decreases gradually；the motion speed gradually increases when the contact surface moves in micro shock tube；in addition，S value can indicate effects of low pressure and small scale in micro shock tube.

micro shock tube；shock wave；contact surface；unsteady flow；numerical simulation

TH47

A

1673-3851（2015）06-0805-07

（责任编辑：康 锋）

2015-01-13

国家自然科学基金项目（51406184）

张光（1988-），男，湖北孝昌人，硕士研究生，主要从事微型激波管方面的研究。

崔宝玲，E-mail：blcui@zstu.edu.cn