基于弱相关界限理论的大型振动试验设备台体系统可靠性分析
2015-10-31冯伟泉
丁 锋,郭 航,冯伟泉,王 剑
(1.西安工业大学 机电工程学院,西安 710021;2.北京卫星环境工程研究所,北京 100094)
基于弱相关界限理论的大型振动试验设备台体系统可靠性分析
丁 锋1,郭 航1,冯伟泉2,王 剑2
(1.西安工业大学 机电工程学院,西安 710021;2.北京卫星环境工程研究所,北京 100094)
航天器振动试验台部分元件在长时间使用的情况下易老化,甚至失效。采用FMEA方法对试验台整体定性分析,得出最薄弱环节;针对试验台中水平滑台的可靠性串联模型,分析并确定了其符合弱相关界限理论。使用传统可靠性公式和弱相关界限理论对串联模型的可靠性进行了计算,通过对比证实,弱相关界限理论比传统可靠性公式更符合实际情况,对水平滑台可靠度的评定更有效。该方法对机械系统可靠度计算具有理论和实际指导意义。
航天器;振动试验台;水平滑台;定性分析;弱相关;可靠性预计
0 引言
目前,我国400 kN双振动台试验系统已运行十余年,尚未经历较大的改造和升级,部分元件存在一定老化难以避免[1],其老化甚至失效将直接影响到航天器的研制工作。因此,针对该振动台试验系统展开可靠性研究,降低试验期间发生意外故障的概率,具有十分重要的意义。
本研究主要针对航天器振动试验台中水平滑台偶有运动不畅、液体静压轴承磨损、轴承安装座螺钉松动、密封失效渗油等问题,进行振动台故障的定性分析及水平滑台可靠性的弱相关定量计算。将弱相关界限理论引入航天器振动试验台可靠性分析中,是对只考虑独立假设串联可靠性模型理论的突破;在机械系统中引入相关性,能够较真实地反映机械设备的实际情况[2]。
1 弱相关界限理论及应用
1.1弱相关界限理论
一般计算机械静态系统可靠度的公式为

其中:Zi=Li-Si(i=1, 2,···, n),Li为强度,Si为应力;Zi为元件i的功能函数;fZ(Z1, Z2,··,Zn)为各功能随机变量的联合概率密度函数,但fZ在实际中较难获得,多重积分不易求解。综合实际考虑,通常根据一些简化假设来计算系统可靠度。
计算机械系统的可靠度过去是在简化条件下,应用独立假设(完全无关)理论和最薄弱环节(完全相关)理论来完成[3-4]。这2种理论均将假设条件绝对化,导出的公式不能广泛适用。结合实际可知机械系统内各零件必然存在不同程度的相关性,而且系统可靠度一般随相关程度的不同而连续变化。为了简化计算系统可靠度,便于判断和减小以上2种极端理论的误差,这里依据相关程度的不同,将连续过程大致分解为5个阶段,取名为阶段连续界限理论[5]。弱相关界限理论是这5个阶段之一的界限理论,它的失效类型为准指数分布,偶然故障占主导,适用于产品复杂、零件数目多的机械系统。如孙玉秋等在印刷机系统弱相关研究应用中,很好地说明了传统可靠性分析的弊端,并提出了理论相关性分析和简化工程高精度的计算方法[5]。
五阶段界限理论数学模型为:设一机械系统由n个元件组成,各元件可靠度为R0, R1, R2,…,Rn-1,且R0<R1≤R2≤…≤Rn-1,各元件的可靠度系数分别为β0, β1, β2,…,βn-1且β0<β1≤β2≤···≤βn-1,由大量的数值分析和推理导出中高可靠度和低可靠度2种情况[6]。
中高可靠度(R0≥0.9或β0≥1.3)时,则有
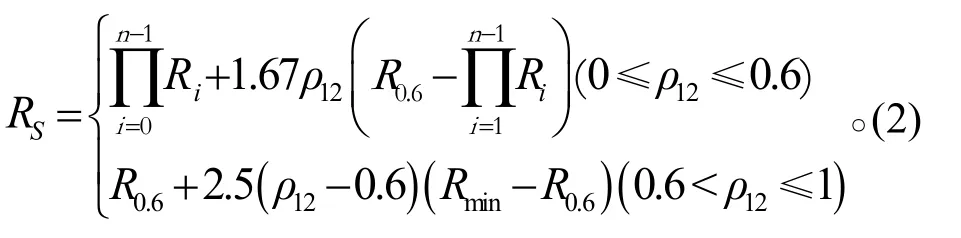
低可靠度(R0<0.9或β0<1.3)时,
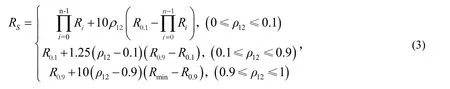
式中:
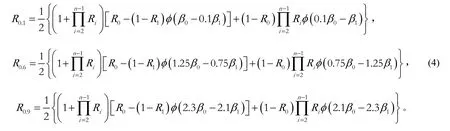
由式(2)~(4)可以看出:
1)当 ρ12=0时,符合独立假设理论,即
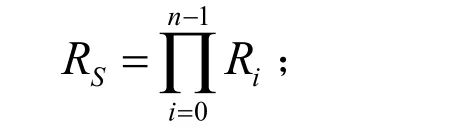
2)当 ρ12=1时,符合最薄弱环节理论,即
3)计算简单,结果是确定的零界限值;
4)RS随着ρ12近似线性单调增长。
然后在 Ditlevsen窄界限理论的验证下得到不同相关条件时系统可靠度为[7-8]
1)完全独立:

2)弱相关:

3)中等相关:
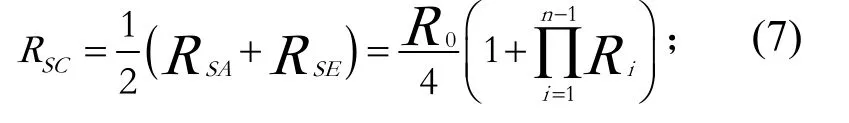
4)强相关:
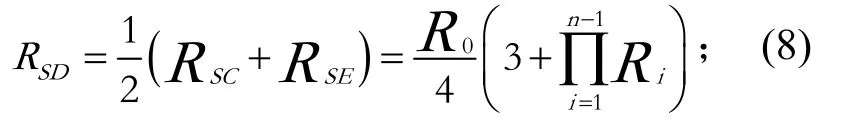
5)完全相关:

1.2定性判断相关程度的准则
在实践中,不难发现影响系统可靠度的相关性主要因素有:产品失效模式;产品元器件数量;各零件间的相关程度,薄弱环节存在与否等。将这些因素综合考虑,划分出完全独立、弱相关、中等相关、强相关以及完全相关5种阶段的相关理论,给出如下理论判断方法[2]。
1)完全独立:失效类型为指数分布,如电子产品系统偶然故障(机械产品不存在这种条件);
2)弱相关:为准指数分布,偶然故障占主要方面,用于产品复杂、零件数目多(如机、电、液等组成)的复杂产品系统可靠度的计算;
3)中等相关:失效类型为非指数分布,故障耗损和偶发故障并重,产品复杂程度中等,零件的可靠度数量级接近,用于一般大多数机械系统可靠度的计算;
4)强相关:分布类型为非指数分布,用于耗损故障为主,系统零件数目不大的比较简单的机械系统,R0较小(系统可能存在薄弱环节),零件之间结构较密切;
5)完全相关:系统分布类型(正态或威布尔分布等)为薄弱件失效分布,完全为耗损故障,产品简单,结构不复杂且零件之间关系密切。
1.3系统可靠性预计的上、下限法
系统可靠性预计是用来预先估计所设计的系统在给定的工作条件下是否达到规定可靠性要求的一种方法,作为一种分析手段提供系统可靠性的相对度量,为寻找设计薄弱环节并做出更改设计的决策提供依据[9-10]。虽然它一般用在产品系统设计阶段,但若将其用在维修统计阶段,简单、快速检验和评定系统可靠度,可粗略得出系统定量的可靠性。
上、下限法基本思想是将复杂的系统先简单地看成是某些单元的串联系统,求出系统可靠度的上限值和下限值,然后逐步考虑系统的复杂情况,逐次求系统可靠度的精确值[11]。一般先求出最低可靠度和最高可靠度,再用几何平均法来得到系统可靠性预计值。
2 大型振动试验设备组成
400 kN双振动台试验系统包含台体子系统(台体、垂直扩展台面、水平滑台)、功放子系统、控制子系统和冷却子系统,如图1所示。

图1 400 kN振动台设备结构Fig.1 The structure of 400 kN vibration test bench
3 台体系统可靠性分析
3.1传统可靠性分析
400 kN振动台试验系统中任一子系统失效都会导致设备故障,因此振动台可靠性模型为串联模型。而水平滑台各个部件也是缺一不可,故滑台的可靠性模型亦为串联模型,如图2所示。
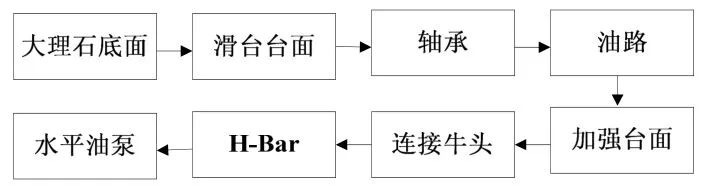
图2 振动试验系统的水平滑台可靠性框图Fig.2 The reliability diagram of horizontal sliding test bench
设水平滑台各零件完全独立,依照传统的串联可靠性模型计算,则有

3.2台体系统FMEA
3.2.1FMEA的分析方法和作用
采用硬件分析法和功能分析法相结合的方式,对400 kN振动台进行FMEA[12-14]。采用2种方法:一种从独立元器件或功能模块级开始,用系统化的方法逐级分析所有的组件和设备;另一种从系统可能的故障出发,自下而上逐级分析可能的故障原因,最终确定系统内部潜在的故障模式及其对系统运行的影响。
FMEA方法是对振动台整体先做故障诊断,分析出薄弱环节,再做可靠性研究与改进,从而提高薄弱环节的可靠性,降低整体机器的故障概率。
3.2.2振动台试验系统常见故障
为有助于400 kN振动台试验系统可靠性研究工作的开展,梳理了自2005年至今的系统故障或异常记录(表1),由表1的统计结果可见,台体系统的故障概率最高,其次是功放系统,两者故障次数共占故障总数的90%以上。台体系统属于机械部件,需定期合理的维保。而功放系统的电子元器件存在整体老化现象,无法更换局部易损件(须整体更换),其寿命相对较短。
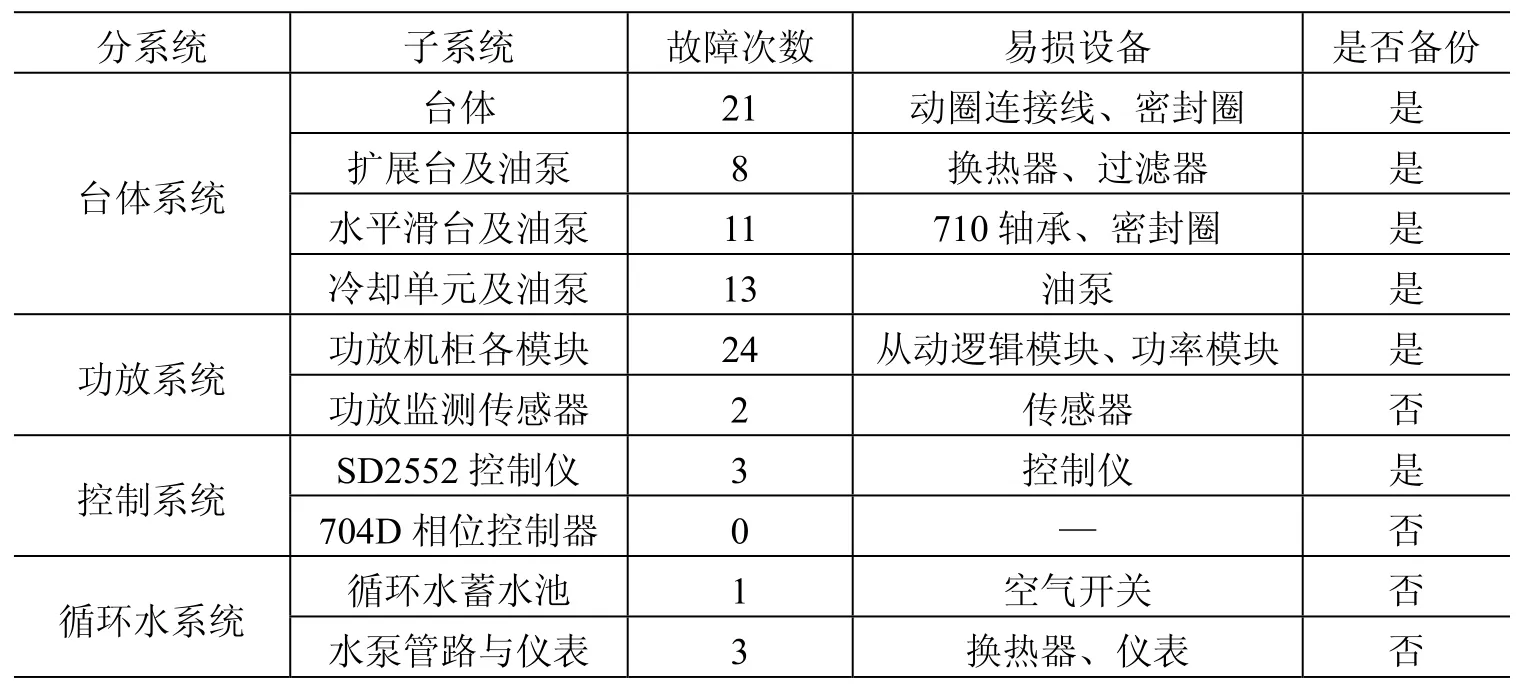
表1 各分系统易损设备及备份统计表Table 1 Failure statistics of equipment and backup of each subsystem
3.3水平滑台的FMEA分析
在航天器试验台中,研究人员对其长期积累的故障概率进行了等级划分(表2),并且对子系统水平滑台做FMEA(表3)。

表2 故障概率等级分类Table 2 Classification of failure probability

表3 水平滑台的FMEATable 3 The FMEA of horizontal sliding table
4 水平滑台系统属于弱相关的分析
4.1 定性分析
在机、电、液、气组成的航天器振动台试验系统中,水平滑台结合实际情况来看无故障工作概率服从准指数分布,原因如下:
1)水平滑台含有机、电、液构件,零件多,主要由偶然故障引发失效。其中液体静压轴承在长期使用后有轻微磨损,一般不会引起失效。水平滑台是机械产品,不会遵从纯电子产品偶然故障的指数分布,而且它的各零件可靠度数量级大多不一样,因此也不符合中等相关的非指数分布。
2)水平滑台可靠性模型虽然是串联方式,但它的零件不是传统可靠性模型下两两之间相互独立的关系,如液压轴承除受到供油的影响外还受到和它接触的零件的外力作用,因此不能直接用传统可靠性公式。
3)在短期重复载荷工况下,水平滑台长期以来发生故障的零件被修复和更换,这就使得相关零件的寿命混杂,最终系统失效率趋于稳定。因此水平滑台符合弱相关界限理论。
4.2弱相关可靠性分析
1)假设水平滑台各个组件独立,由传统串联可靠度公式(10),得最低可靠度为

最高可靠度为

采用几何平均法得到水平滑台可靠性预计值为
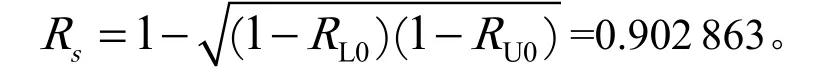
2)由于滑台长期被维修,因而遵循弱相关,用公式(6)得最低可靠度为
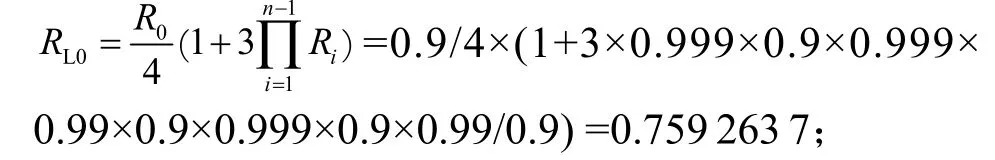
最高可靠度为
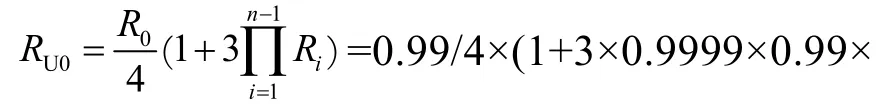
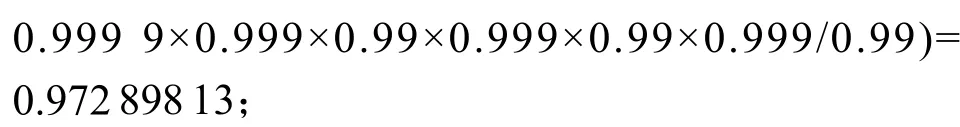
系统可靠度预计值为
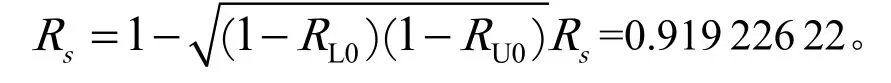
由以上计算可以看出,在运用上、下限法计算系统可靠性预计值时,弱相关理论的计算结果较传统串联可靠度高,说明传统可靠度公式计算出的可靠度偏保守,而弱相关公式考虑到系统中各零件完全独立的情况几乎不存在,计算出的可靠度更能反映实际情况。
4.3验证情况
由表3能看出水平滑台各部分失效不是完全独立的,如轴承失效可能是油路或者支座螺钉力矩不足引起的,加强台面失效可能是螺套被拔出或者台面变形引起的,显然各部分存在一定的相关性,选用传统串联乘积公式会造成结果失真。而且水平滑台的失效模型主要由偶然失效引起,故障零件长期经历维修使其失效率趋于稳定,因而符合弱相关界限理论的条件,故选用弱相关理论模型进行计算比选用传统可靠性串联模型更符合实际情况。
5 结束语
通过用FMEA方法对航天器振动台试验系统可靠性做定性分析,找出台体易出现的故障;对台体薄弱环节之水平滑台做可靠性研究,有助于提高其可靠性以降低整体机器的故障概率。而在水平滑台中,用系统可靠性预计值来粗略评估,虽然没有得到精确值,但通过对比发现,弱相关界限理论比零件完全独立下的传统可靠性公式更符合实际情况,对研究水平滑台可靠度更为有效。而且在其他机械系统中,各零件完全独立的情况几乎不存在,只要找到各零件的相关关系,用 5个连续过程分析,就可获得较接近工程实际的可靠度。
(
)
[1]张巧寿.振动试验系统现状与发展[J].机电新产品导报, 2001(9): 118-121 Zhang Qiaoshou.Present situation and development ofvibration test system[J].Machinery & Electrical New Products Guide, 2001(9): 118-121
[2]孙玉秋, 张祖明.基于相关性的机械系统可靠性设计理论[J].机械科学与技术, 2006, 25(5): 576-579 Sun Yuqiu, Zhang Zuming.Relevance-based reliability theory of mechanical systems[J].Mechanical Science and Technology, 2006, 25(5): 576-579
[3]芮延年, 傅戈雁.现代可靠性设计[M].北京: 国防工业出版社, 2007: 235-255
[4]刘惟信.机械可靠性设计[M].北京: 清华大学出版社,2006: 228-330
[5]孙玉秋, 张祖明.机械系统可靠度计算方法—阶段连续界限理论[J].机械设计与制造, 2001(2): 3-5 Sun Yuqiu, Zhang Zuming.Method for reliability calculation of mechanical system-stage continuous boundary theory[J].Machinery Design & Manufacture,2001(2):3-5
[6]喻天翔, 张祖明, 张选生, 等.零件相关的机械产品的系统可靠性设计(SRD)新理论[J].机械设计与制造,2002(6): 1-3 Yu Tianxiang, Zhang Zuming, Zhang Xuansheng, et al.The new theory of reliability design for mechanical system of element related[J].Machinery Design & Manufacture, 2002(6): 1-3
[7]Ditlevsen O.Narrow reliability bounds for structural system[J].Journal of Structural Mechanics, 1979, 7(4):453-472
[8]喻天翔, 宋笔锋, 万方义, 等.机械零件多失效模式相关可靠度算法研究[J].机械强度, 2006, 28(4): 508-511 Yu Tianxiang, Song Bifeng, Wan Fangyi, et al.Research on calculating the reliability of mechanical component with correlaed failure modes[J].Journal of Mechanical Strength, 2006, 28(4): 508-511
[9]王远达, 宋笔锋.系统可靠性预计方法综述[J].飞机设计, 2008, 28(1): 38-40 Wang Yuanda, Song Bifeng.Overview of system reliability prediction method[J].Aircraft Design, 2008,28(1): 38-40
[10]Zhao Wei, Tao Tao.A dynamic particle filter-support vector regression method for reliability prediction[J].Reliability Engineering & System Safety, 2013, 119:109-116
[11]董哲.复杂系统可靠性上下限预测的一种简单方法[J].电测与仪表, 2000, 37(2): 9-11 Dong Zhe.A simple method for reliable forecast of upper and lower limit to complex systems[J].Electrical Measurement &Instrumentation, 2000, 37(2): 9-11
[12]刘志全, 宫颖.航天器产品FMEA工作有效性的思考[J].航天器工程, 2011, 20(1): 142-146 Liu Zhiquan, Gong Ying.Consideration about the validity of aerospace product FMEA[J].Spacecraft Engineering, 2011, 20(1): 142-146
[13]盛江, 刘国青.空间环境模拟器的FMEA分析方法[J].航天器环境工程, 2008, 25(4): 395-400 Sheng Jiang, Liu Guoqing.The FMEA method in large space environment simulators[J].Spacecraft Environment Engineering, 2008, 25(4): 395-400
[14]Shen Fengxia.Failure modes and effects analysis of dynamic environment test[C]//8thInternational Conference on Reliability, Maintainability and Safety(ICRMS 2009), 2009: 353-362
(编辑:冯 妍)
Reliability analysis of large vibration test equipment platform system based on weak correlation theory
Ding Feng1, Guo Hang1, Feng Weiquan2, Wang Jian2
(1.School of Mechanical and Electrical Engineering, Xi'an Technological University, Xi'an 710021, China;2.Beijing Institute of Spacecraft Environment Engineering, Beijing 100094, China)
In the vibration test of spacecraft, some of its components will undergo the processes of aging, even failure because of long time use.For a qualitative analysis, the FMEA method is used to analyze the overall test bench, and the weakest link for the test bench is identified.For a horizontal sliding table's reliability series model in the subsystem, it is shown that it complies with the weak correlation theory.Then, the traditional reliability formula and the weak correlation are used, respectively, to predict the reliability of the model.A comparison shows that the weak correlation is better than the traditional reliability formula under the condition that all parts are not completely independent according to the actual situation.That is to say it is more effective for the reliability assessment of the horizontal sliding bench.The method is of theoretical and practical significance for mechanical system reliability calculations.
spacecraft; vibration test bench; horizontal sliding test bench; qualitative analysis; weak correlation;reliability prediction
V416; O329; TB114.3
A
1673-1379(2015)06-0668-06
10.3969/j.issn.1673-1379.2015.06.020
丁 锋(1968—),男,博士学位,教授,主要研究方向为设备状态监测及维护、可靠性评估与优化设计等。E-mail: dd_feng@sina.com。
2015-05-07;
2015-12-12
可靠性与环境工程技术重点实验室开放基金支持;国家自然科学基金项目(编号:51275374);陕西省教育厅科研计划项目(编号:11JK0860)。
