二重积分换元法证明及推广新思路

安明松　王旭琴　冯拥武

（1.中国地质大学（北京）地学院，北京　100083；2.中央民族大学数理学院，北京　100081；3.西北民族大学信息学院，甘肃兰州　730124）

二重积分换元法证明及推广新思路

安明松1王旭琴2冯拥武3

（1.中国地质大学（北京）地学院，北京100083；2.中央民族大学数理学院，北京100081；3.西北民族大学信息学院，甘肃兰州730124）

本文考虑到现在很多大学数学教材中省略了越来越多的教学拓展内容，而满足不了一些学有余力同学对知识的本质探索与追求的现状之后，综合前辈们各种巧妙的思路，很基础地利用对微元体进行稳定体式完全划分的思想结合n维稳定体体积公式，给出了一种证明二重积分换元法的新思路，并由此展开，对其进行了发散推广，扩展到三维及 n维的情况。

二重积分换元法微元体积n维稳定体

重积分贯穿着空间解析几何知识与数学分析知识的综合应用，其核心的内涵是一种映射，特别是微元部分的转换。积分域的变换在自变量之间的变换时就已经确定了，积分函数的变化只是将其自变量作相应的变换。抓住微元部分这个突破口，利用变换函数确定微元部分各个顶点的坐标，通过n维空间中的稳定体的体积公式可以计算变换前后的微元部分的相互关系。只要把微元部分按所得关系带入原来的积分即得换元公式。

1　n维空间稳定体的体积公式及推导

定理：n维空间中的稳定体的体积为：

2　证明二重积分换元公式

定理：设f（x，y）在xoy平面上的闭区域D上连续，变换 T：x=x（u，v）， y=y（u，v）

将uvw平面上的闭区域'D变为xoy平面上的D，且满足：

图1　uvw平面上的闭区域'D

图2　xoy平面上的闭区域D

图3　

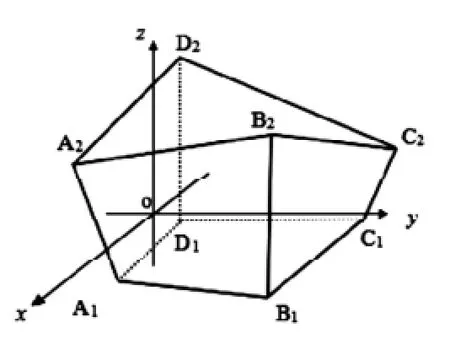
图4　

（1）x（u，v），y（u，v）在'D上具有一阶连续偏导数；

（2）在'D上雅克比式

（3）变换T：'D→D是一对一的，

则有：

证明：如图1、2所示，表示从uov到xoy的变换。

uov坐标系：'σd=dudv=2h，

xoy坐标系：1M（1x=x（u，v），1y=y（u，v）），2M（x（u，v）+ux（u，v）h+o（h），y（u，v）+uy（u，v）h+o（h））

M3（x（u，v）+xu（u，v）h+xv（u，v）h+o（h），y（u，v）+yu（u，v）h+yv（u，v）h+o（h））

M4（x（u，v）+xv（u，v）h+o（h），y（u，v）+yv（u，v）h+o（h））n维空间中的稳定体的体积公式中取n=2 ，则有：

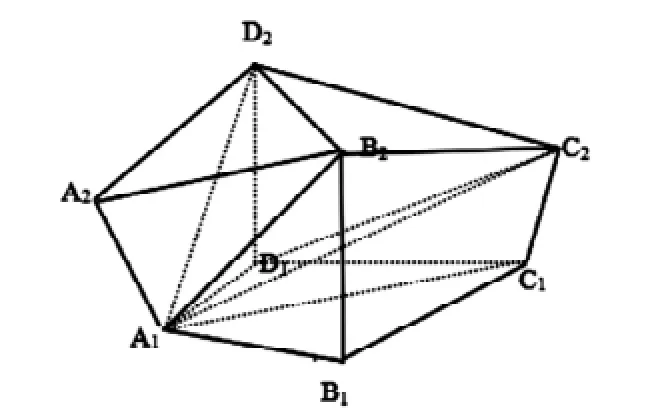
图5　

3　二重积分换元公式的推广

3.1三重积分换元公式

定理：设变换T：x=x（u，v，w），y=y（u，v，w），z=z（u，v，w）把uvw空间中的区域'Ω一对一地映成空间区域Ω，并设函数x（u，v，w），y（u，v，w），z（u，v，w）及它们的一阶偏导数在'Ω内连续且行列式

证明：主要思路已经给出，现在着手计算体积微元，体积微元如下图（图3是'dV，图4是dV）对应关系。

uvw坐标系：3A（u，v，w），3B（u，v+dv，w）3C，（u+du， v+dv），3D（u+du，v，w），4A（u，v，w+dw）

B4（u，v+dv，w+du），C4（u+du，v+dv，w+dw），D4（u+du，v，w+dw），dV'=dudvdw

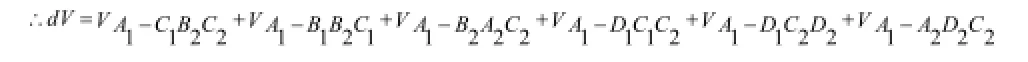
同理应用n维空间中的稳定体的体积定理，取n=3，则有：

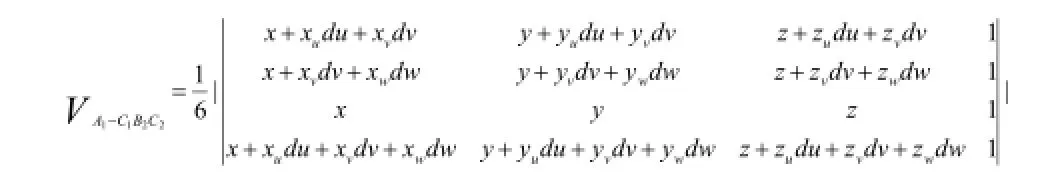
同理可证：

3.2n重积分的换元公式的推导

f （nxxx，，，21…）在Ω上可积，则

为了计算（实际上所有合法的稳定体体积都相等），取以下特殊点：

A1（x1（u1，u2，…，un），x2（u1，u2，…，un），...，xn（u1，u2，…，un）），An+1（x1（u1+du1，u2+du2，…，un+dun），x2（u1+du1，u2+du2，…，un+dun），...，xn（u1+du1，u2+du2，…，un+dun））。

故n重积分换元公式得证。

［1］陈志杰.高等代数与解析几何上册［M］.高等教育出版社，2000.

［2］李小平.n维空间中距离公式、稳定体体积公式以及勾股定理的拓广［J］.http：//www.docin.com/p-362313297.html，2012.3.15.

［3］冯文强，杨汉生.二重积分换元法的另一种证法及推广［J］.西南科技大学《高教研究》，2006，（4）：69-74.

［4］同济大学数学系.高等数学（下）［M］.第四版.北京：高等教育出版社，2007.

［5］张筑生.数学分析新讲第二册［M］.北京：北京大学出版社，1990（2010.4重印）.331-370.

［6］陈兆斗，褚宝增.高等数学（下册）［M］.北京：北京大学出版社，2008. 99-104.

［7］陈兆斗，郑连存，王辉，李为东.大学生数学竞赛习题精讲［M］.北京：清华大学出版社，2010.59-119.

In this paper， considering the many university mathematics textbook omitted expand more and more teaching content， and there is spare capacity can not meet some of the students on the current situation after the nature of exploration and the pursuit of knowledge， integrated predecessors variety of ingenious ideas， very basic use of the micro unit stabilized completely divided ideological postures combined n-dimensional stable body volume formula gives a proof of Double Integral element new ideas， and thus expanded its divergence promotion， expansion to three-dimensional and n-dimensional case.

double integral；integration by substitution；micro volume； n-dimensional stable body